9.1.3 作轴对称图形 培优练习(含答案)
文档属性
| 名称 | 9.1.3 作轴对称图形 培优练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-01 11:31:52 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
9.1.3作轴对称图形培优练习华东师大版2024—2025学年七年级下册
一、选择题
1.下面是四位同学作△ABC关于直线MN的轴对称图形,其中正确的是( )
A.B. C.D.
2.如图,在四边形ABCD中,请在所给的图形中进行操作:
①作点A关于BD的对称点P;
②作射线PC交BD于点Q;
③连接AQ.试用所作图形进行判断,下列选项中正确的是( )
A.∠PCB=∠AQB
B.∠PCB<∠AQB
C.∠PCB>∠AQB
D.以上三种情况都有可能
3.不能用无刻度直尺直接准确画出下列轴对称图形的所有对称轴的是( )
A. B. C. D.
4.如图,在3×3的正方形的网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的△ABC为格点三角形,在图中最多能画出( )个格点三角形与△ABC成轴对称.
A.6个 B.5个
C.4个 D.3个
5.如图,分别以△ABC的边AB,AC所在直线为对称轴作△ABC的对称图形△ABD和△ACE,∠BAC=150°,线段BD与CE相交于点O,连接BE、ED、DC、OA.有如下结论:①∠EAD=90°;②∠BOE=60°;③OA平分∠BOC;④EAED;⑤BP=EQ.其中正确的结论个数是( )
A.4个 B.3个 C.2个 D.1个
二、填空题
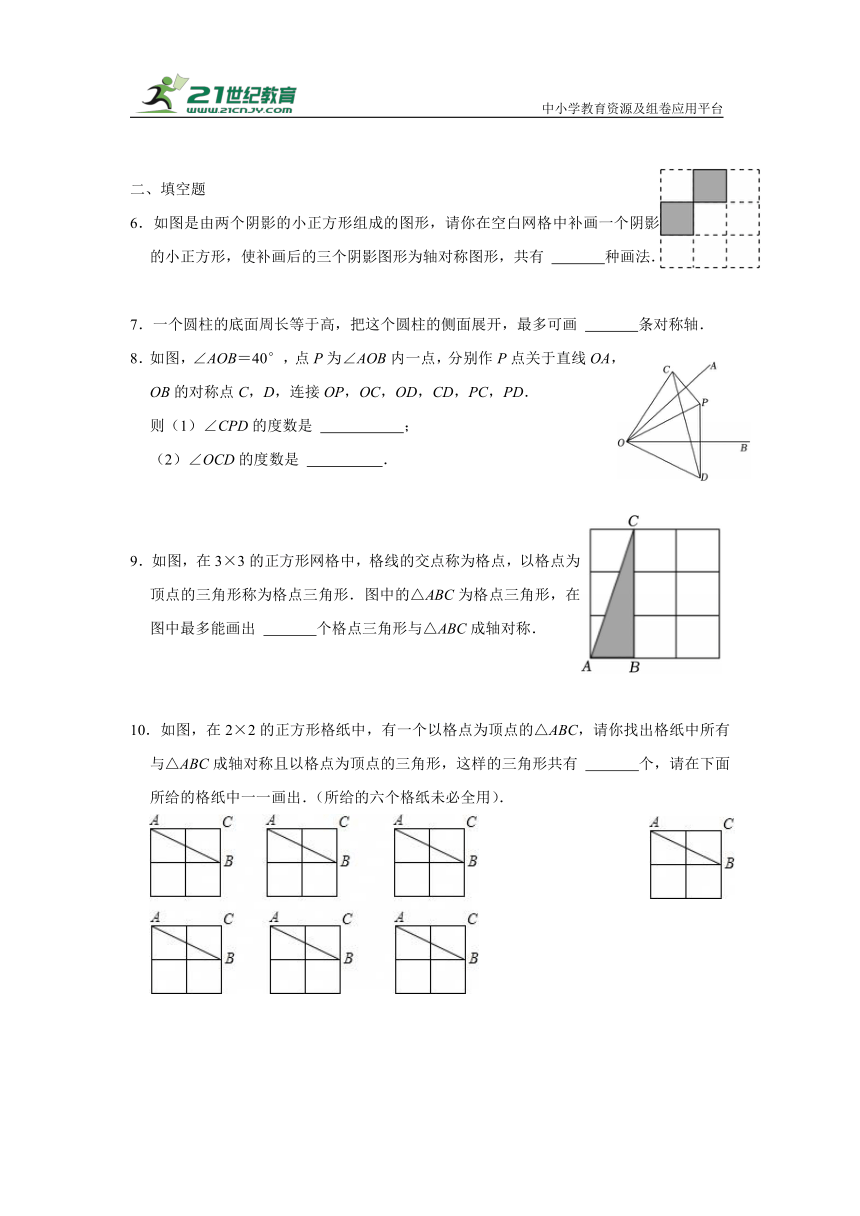
6.如图是由两个阴影的小正方形组成的图形,请你在空白网格中补画一个阴影的小正方形,使补画后的三个阴影图形为轴对称图形,共有 种画法.
7.一个圆柱的底面周长等于高,把这个圆柱的侧面展开,最多可画 条对称轴.
8.如图,∠AOB=40°,点P为∠AOB内一点,分别作P点关于直线OA,OB的对称点C,D,连接OP,OC,OD,CD,PC,PD.
则(1)∠CPD的度数是 ;
(2)∠OCD的度数是 .
9.如图,在3×3的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形.图中的△ABC为格点三角形,在图中最多能画出 个格点三角形与△ABC成轴对称.
10.如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且以格点为顶点的三角形,这样的三角形共有 个,请在下面所给的格纸中一一画出.(所给的六个格纸未必全用).
三、解答题
11.如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(﹣1,3),B(﹣3,﹣1),C(0,﹣2),直线l上各点的横坐标都为1.
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)若△ABC和△A2B2C2关于直线l对称,则点A2的坐标为 ,点B2的坐标为 ,点C2的坐标为 .
12.在平面直角坐标系中,△ABC的顶点坐标是A(﹣4,1),B(﹣3,5),C(﹣1,4).
(1)画出△ABC关于y轴对称后的△A1B1C1;
(2)点A1坐标 ,B1坐标 ,C1坐标 ;
(3)△AOC1的面积为 .
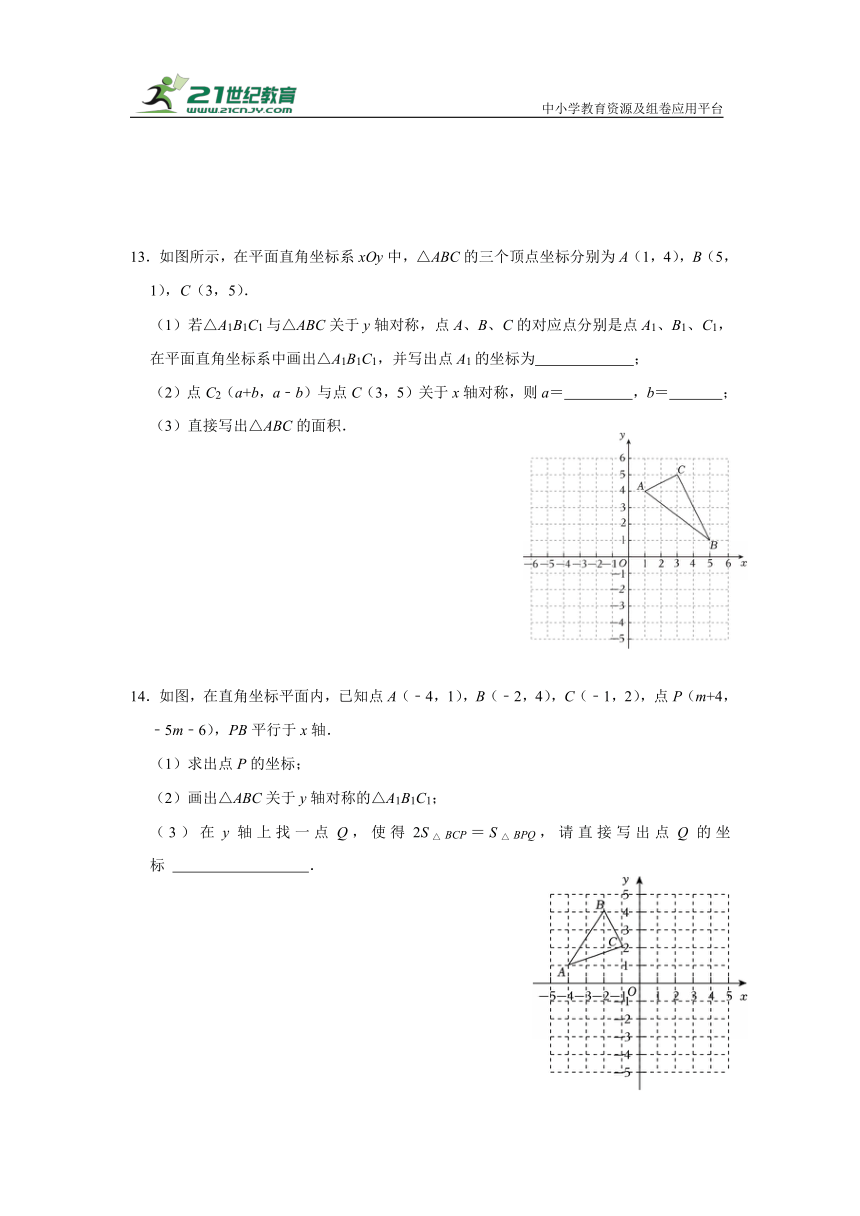
13.如图所示,在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(1,4),B(5,1),C(3,5).
(1)若△A1B1C1与△ABC关于y轴对称,点A、B、C的对应点分别是点A1、B1、C1,在平面直角坐标系中画出△A1B1C1,并写出点A1的坐标为 ;
(2)点C2(a+b,a﹣b)与点C(3,5)关于x轴对称,则a= ,b= ;
(3)直接写出△ABC的面积.
14.如图,在直角坐标平面内,已知点A(﹣4,1),B(﹣2,4),C(﹣1,2),点P(m+4,﹣5m﹣6),PB平行于x轴.
(1)求出点P的坐标;
(2)画出△ABC关于y轴对称的△A1B1C1;
(3)在y轴上找一点Q,使得2S△BCP=S△BPQ,请直接写出点Q的坐标 .
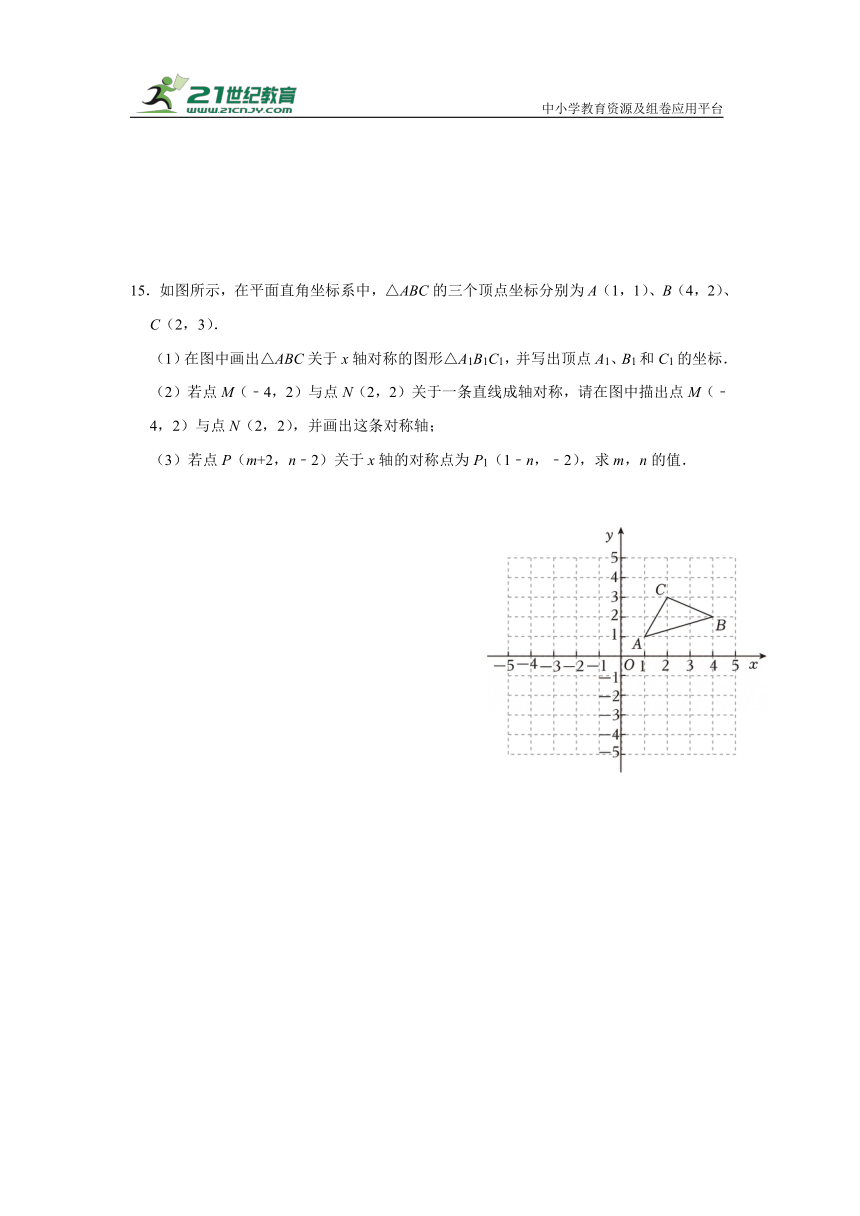
15.如图所示,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,1)、B(4,2)、C(2,3).
(1)在图中画出△ABC关于x轴对称的图形△A1B1C1,并写出顶点A1、B1和C1的坐标.
(2)若点M(﹣4,2)与点N(2,2)关于一条直线成轴对称,请在图中描出点M(﹣4,2)与点N(2,2),并画出这条对称轴;
(3)若点P(m+2,n﹣2)关于x轴的对称点为P1(1﹣n,﹣2),求m,n的值.
参考答案
一、选择题
题号 1 2 3 4 5
答案 B C D A B
二、填空题
6.【解答】解:根据轴对称图形可作如图所示:
共有5种画法,
故答案为:5.
7.【解答】解:一个圆柱的底面周长等于高,把这个圆柱的侧面展开是一个正方形,如图,正方形最多可画4条对称轴;
故答案为:4.
8.【解答】解:(1)∵点P,C关于直线OA对称,
∴OP=OC,∠COA=∠POA∠COP,
∴∠OCP=∠OPC;
同理可知∠POB=∠DOB∠POD,
∴∠OPD=∠ODP,
∵∠AOB=40°,
∴∠COP+∠POD=2∠AOB=80°,
∴∠CPD=∠OPC+∠OPD140°.
故答案为:140°.
(2)∵点P,C关于直线OA对称,点P,D关于直线OB对称,
∴OP=OC,OP=OD,
∴OC=OD,
∴∠OCD=∠ODC.
由(1)知,∠COD=∠COP+∠POD=2∠AOB=80°,
∴∠OCD50°.
故答案为:50°.
9.【解答】解:如图,最多能画出6个格点三角形与△ABC成轴对称.
故答案为:6.
10.【解答】解:与△ABC成轴对称且以格点为顶点的三角形如图:
共5个.
三、参考答案
11.【解答】解:(1)如图,△A1B1C1即为所求.
(2)如图:A2(3,3),B2(5,﹣1),C2(2,﹣2).
故答案为:(3,3),(5,﹣1),(2,﹣2).
12.【解答】解:(1)如图,△A1B1C1即为所求.
(2)由图可得,点A1(4,1),B1(3,5),C1(1,4).
故答案为:(4,1);(3,5);(1,4).
(3)△AOC1的面积为.
故答案为:.
13.【解答】解:(1)△ABC关于y轴对称的△A1B1C1,如图1即为所求;
由图可知,A1(﹣1,4),
故答案为:(﹣1,4);
(2)∵点C2(a+b,a﹣b)与点C(3,5)关于x轴对称,
∴C2的坐标为(3,﹣5),
∴,
∴a=﹣1,b=4,
故答案为:﹣1,4;
(3)由题意得,S△ABC=4×41×23×42×4=5.
14.【解答】解:(1)∵B(﹣2,4),点P(m+4,﹣5m﹣6),PB平行于x轴,
∴﹣5m﹣6=4,解得:m=﹣2,则m+4=2,
∴P(2,4);
(2)如图所示;
(3)∵B(﹣2,4),C(﹣1,2),P(2,4),设Q(0,n),
∴BP=4,
则S△BCPPB |yC﹣yB|4×|2﹣4|=4,
∵2S△BCP=S△BPQ,
∴S△BPQBP|yQ﹣yB|4×|n﹣4|=8,
即:|n﹣4|=4,
∴n=0或n=8,
∴点Q的坐标为(0,0)或(0,8);
故答案为:(0,0)或(0,8).
15.【解答】解:(1)如图,△A1B1C1即为所求,A1(1,﹣1),B1(4,﹣2),C1(2,﹣3);
(2)如图,点M,点N,直线l即为所求;
(3)∵点P(m+2,n﹣2)关于x轴的对称点为P1(1﹣n,﹣2),
∴,
解得.
9.1.3作轴对称图形培优练习华东师大版2024—2025学年七年级下册
一、选择题
1.下面是四位同学作△ABC关于直线MN的轴对称图形,其中正确的是( )
A.B. C.D.
2.如图,在四边形ABCD中,请在所给的图形中进行操作:
①作点A关于BD的对称点P;
②作射线PC交BD于点Q;
③连接AQ.试用所作图形进行判断,下列选项中正确的是( )
A.∠PCB=∠AQB
B.∠PCB<∠AQB
C.∠PCB>∠AQB
D.以上三种情况都有可能
3.不能用无刻度直尺直接准确画出下列轴对称图形的所有对称轴的是( )
A. B. C. D.
4.如图,在3×3的正方形的网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的△ABC为格点三角形,在图中最多能画出( )个格点三角形与△ABC成轴对称.
A.6个 B.5个
C.4个 D.3个
5.如图,分别以△ABC的边AB,AC所在直线为对称轴作△ABC的对称图形△ABD和△ACE,∠BAC=150°,线段BD与CE相交于点O,连接BE、ED、DC、OA.有如下结论:①∠EAD=90°;②∠BOE=60°;③OA平分∠BOC;④EAED;⑤BP=EQ.其中正确的结论个数是( )
A.4个 B.3个 C.2个 D.1个
二、填空题
6.如图是由两个阴影的小正方形组成的图形,请你在空白网格中补画一个阴影的小正方形,使补画后的三个阴影图形为轴对称图形,共有 种画法.
7.一个圆柱的底面周长等于高,把这个圆柱的侧面展开,最多可画 条对称轴.
8.如图,∠AOB=40°,点P为∠AOB内一点,分别作P点关于直线OA,OB的对称点C,D,连接OP,OC,OD,CD,PC,PD.
则(1)∠CPD的度数是 ;
(2)∠OCD的度数是 .
9.如图,在3×3的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形.图中的△ABC为格点三角形,在图中最多能画出 个格点三角形与△ABC成轴对称.
10.如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且以格点为顶点的三角形,这样的三角形共有 个,请在下面所给的格纸中一一画出.(所给的六个格纸未必全用).
三、解答题
11.如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(﹣1,3),B(﹣3,﹣1),C(0,﹣2),直线l上各点的横坐标都为1.
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)若△ABC和△A2B2C2关于直线l对称,则点A2的坐标为 ,点B2的坐标为 ,点C2的坐标为 .
12.在平面直角坐标系中,△ABC的顶点坐标是A(﹣4,1),B(﹣3,5),C(﹣1,4).
(1)画出△ABC关于y轴对称后的△A1B1C1;
(2)点A1坐标 ,B1坐标 ,C1坐标 ;
(3)△AOC1的面积为 .
13.如图所示,在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(1,4),B(5,1),C(3,5).
(1)若△A1B1C1与△ABC关于y轴对称,点A、B、C的对应点分别是点A1、B1、C1,在平面直角坐标系中画出△A1B1C1,并写出点A1的坐标为 ;
(2)点C2(a+b,a﹣b)与点C(3,5)关于x轴对称,则a= ,b= ;
(3)直接写出△ABC的面积.
14.如图,在直角坐标平面内,已知点A(﹣4,1),B(﹣2,4),C(﹣1,2),点P(m+4,﹣5m﹣6),PB平行于x轴.
(1)求出点P的坐标;
(2)画出△ABC关于y轴对称的△A1B1C1;
(3)在y轴上找一点Q,使得2S△BCP=S△BPQ,请直接写出点Q的坐标 .
15.如图所示,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,1)、B(4,2)、C(2,3).
(1)在图中画出△ABC关于x轴对称的图形△A1B1C1,并写出顶点A1、B1和C1的坐标.
(2)若点M(﹣4,2)与点N(2,2)关于一条直线成轴对称,请在图中描出点M(﹣4,2)与点N(2,2),并画出这条对称轴;
(3)若点P(m+2,n﹣2)关于x轴的对称点为P1(1﹣n,﹣2),求m,n的值.
参考答案
一、选择题
题号 1 2 3 4 5
答案 B C D A B
二、填空题
6.【解答】解:根据轴对称图形可作如图所示:
共有5种画法,
故答案为:5.
7.【解答】解:一个圆柱的底面周长等于高,把这个圆柱的侧面展开是一个正方形,如图,正方形最多可画4条对称轴;
故答案为:4.
8.【解答】解:(1)∵点P,C关于直线OA对称,
∴OP=OC,∠COA=∠POA∠COP,
∴∠OCP=∠OPC;
同理可知∠POB=∠DOB∠POD,
∴∠OPD=∠ODP,
∵∠AOB=40°,
∴∠COP+∠POD=2∠AOB=80°,
∴∠CPD=∠OPC+∠OPD140°.
故答案为:140°.
(2)∵点P,C关于直线OA对称,点P,D关于直线OB对称,
∴OP=OC,OP=OD,
∴OC=OD,
∴∠OCD=∠ODC.
由(1)知,∠COD=∠COP+∠POD=2∠AOB=80°,
∴∠OCD50°.
故答案为:50°.
9.【解答】解:如图,最多能画出6个格点三角形与△ABC成轴对称.
故答案为:6.
10.【解答】解:与△ABC成轴对称且以格点为顶点的三角形如图:
共5个.
三、参考答案
11.【解答】解:(1)如图,△A1B1C1即为所求.
(2)如图:A2(3,3),B2(5,﹣1),C2(2,﹣2).
故答案为:(3,3),(5,﹣1),(2,﹣2).
12.【解答】解:(1)如图,△A1B1C1即为所求.
(2)由图可得,点A1(4,1),B1(3,5),C1(1,4).
故答案为:(4,1);(3,5);(1,4).
(3)△AOC1的面积为.
故答案为:.
13.【解答】解:(1)△ABC关于y轴对称的△A1B1C1,如图1即为所求;
由图可知,A1(﹣1,4),
故答案为:(﹣1,4);
(2)∵点C2(a+b,a﹣b)与点C(3,5)关于x轴对称,
∴C2的坐标为(3,﹣5),
∴,
∴a=﹣1,b=4,
故答案为:﹣1,4;
(3)由题意得,S△ABC=4×41×23×42×4=5.
14.【解答】解:(1)∵B(﹣2,4),点P(m+4,﹣5m﹣6),PB平行于x轴,
∴﹣5m﹣6=4,解得:m=﹣2,则m+4=2,
∴P(2,4);
(2)如图所示;
(3)∵B(﹣2,4),C(﹣1,2),P(2,4),设Q(0,n),
∴BP=4,
则S△BCPPB |yC﹣yB|4×|2﹣4|=4,
∵2S△BCP=S△BPQ,
∴S△BPQBP|yQ﹣yB|4×|n﹣4|=8,
即:|n﹣4|=4,
∴n=0或n=8,
∴点Q的坐标为(0,0)或(0,8);
故答案为:(0,0)或(0,8).
15.【解答】解:(1)如图,△A1B1C1即为所求,A1(1,﹣1),B1(4,﹣2),C1(2,﹣3);
(2)如图,点M,点N,直线l即为所求;
(3)∵点P(m+2,n﹣2)关于x轴的对称点为P1(1﹣n,﹣2),
∴,
解得.
