第26章反比例函数章末精选题练习(含解析)-2024-2025学年数学九年级下册人教版
文档属性
| 名称 | 第26章反比例函数章末精选题练习(含解析)-2024-2025学年数学九年级下册人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-01 12:59:32 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第26章反比例函数章末精选题练习-2024-2025学年数学九年级下册人教版
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知点,,在反比例函数的图象上,下列结论正确的是( )
A. B. C. D.
2.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压(千帕)是气体体积(立方米)的反比例函数,其图像如图所示(千帕是一种压强单位),当气球的体积是0.8立方米时,气球内的气压是( )千帕
A.100 B.110 C.120 D.130
3.已知反比例函数的图象位于第一、三象限,则的取值范围是( )
A. B. C. D.
4.一次函数(k为常数,且)和反比例函数在同一平面直角坐标系中的图象可能是( ).
A. B.
C. D.
5.如图,直线与双曲线交于,两点,过点作轴,垂足为点,连接,若,则的值为( )
A. B. C. D.
6.如图,直线与双曲线交于点和点,则不等式的解集是( )
A.或 B.
C.或 D.或
二、填空题
7.已知反比例函数的图象的一支位于第二象限,则常数m的取值范围是 .
8.负责鱼菜共生系统建设的工程队平均每天的工作量(亩/天)与完成建设所需的时间(天)之间的函数图象如图所示,若该工程队每天最多建设0.5亩,则该工程队完成全部鱼菜共生系统的建设最快需要 天.
9.如图,直线l:与 反 比 例 函 数的 图 象 交 于 点A, 与 x 轴交于点B, 将 线 段 绕 点B逆时针旋转至线段,若点C恰好也在反比例函数图象上,则k的值为 ·
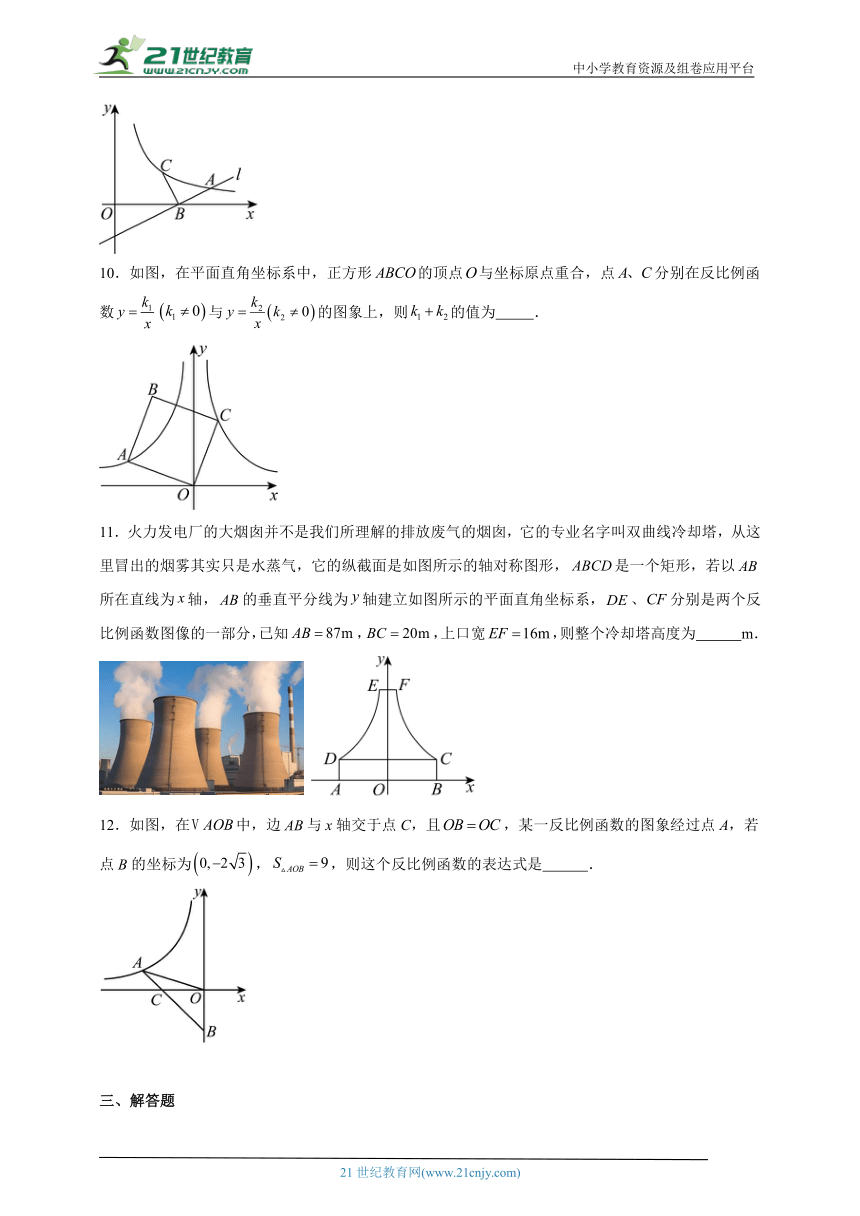
10.如图,在平面直角坐标系中,正方形的顶点与坐标原点重合,点分别在反比例函数与的图象上,则的值为 .
11.火力发电厂的大烟囱并不是我们所理解的排放废气的烟囱,它的专业名字叫双曲线冷却塔,从这里冒出的烟雾其实只是水蒸气,它的纵截面是如图所示的轴对称图形,是一个矩形,若以所在直线为轴,的垂直平分线为轴建立如图所示的平面直角坐标系,、分别是两个反比例函数图像的一部分,已知,,上口宽,则整个冷却塔高度为 m.
12.如图,在中,边与x轴交于点C,且,某一反比例函数的图象经过点A,若点B的坐标为,,则这个反比例函数的表达式是 .
三、解答题
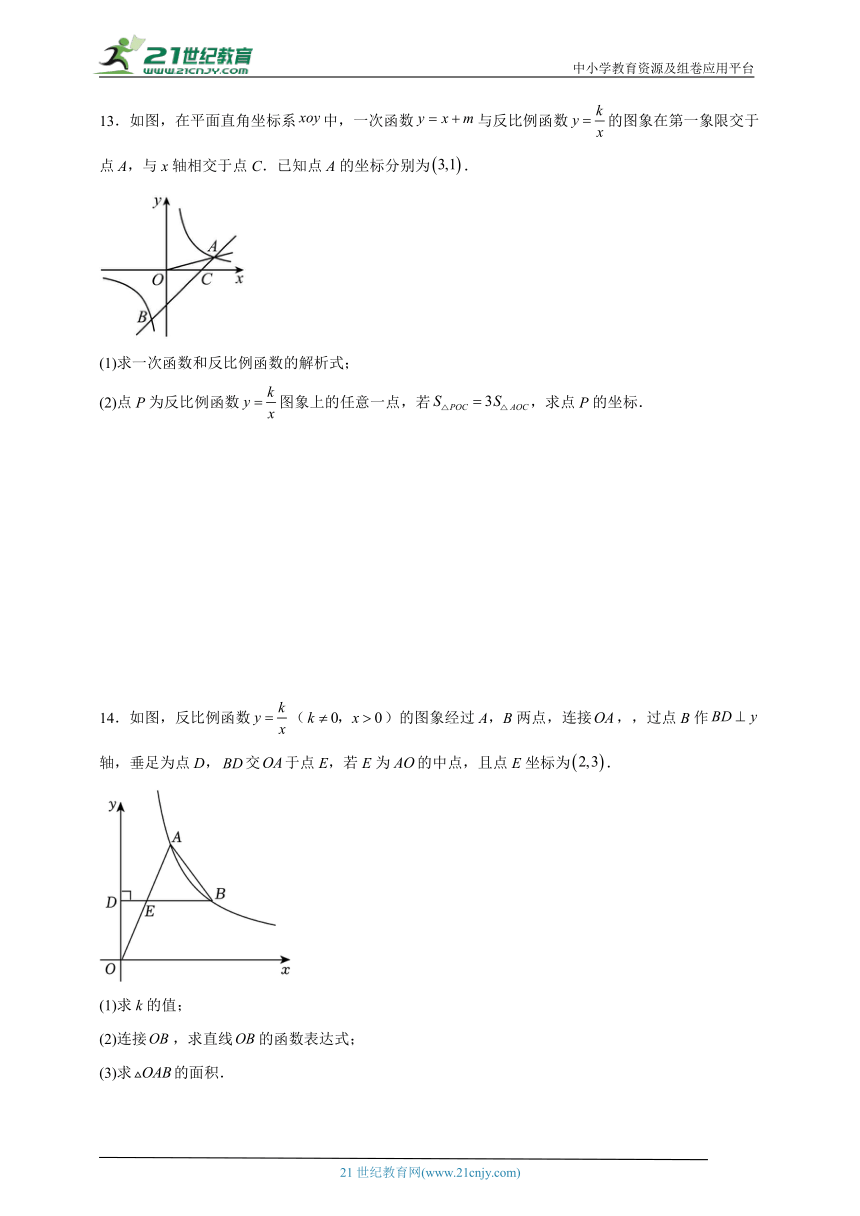
13.如图,在平面直角坐标系中,一次函数与反比例函数的图象在第一象限交于点A,与x轴相交于点C.已知点A的坐标分别为.
(1)求一次函数和反比例函数的解析式;
(2)点P为反比例函数图象上的任意一点,若,求点P的坐标.
14.如图,反比例函数()的图象经过A,B两点,连接,,过点B作轴,垂足为点D,交于点E,若E为的中点,且点E坐标为.
(1)求k的值;
(2)连接,求直线的函数表达式;
(3)求的面积.
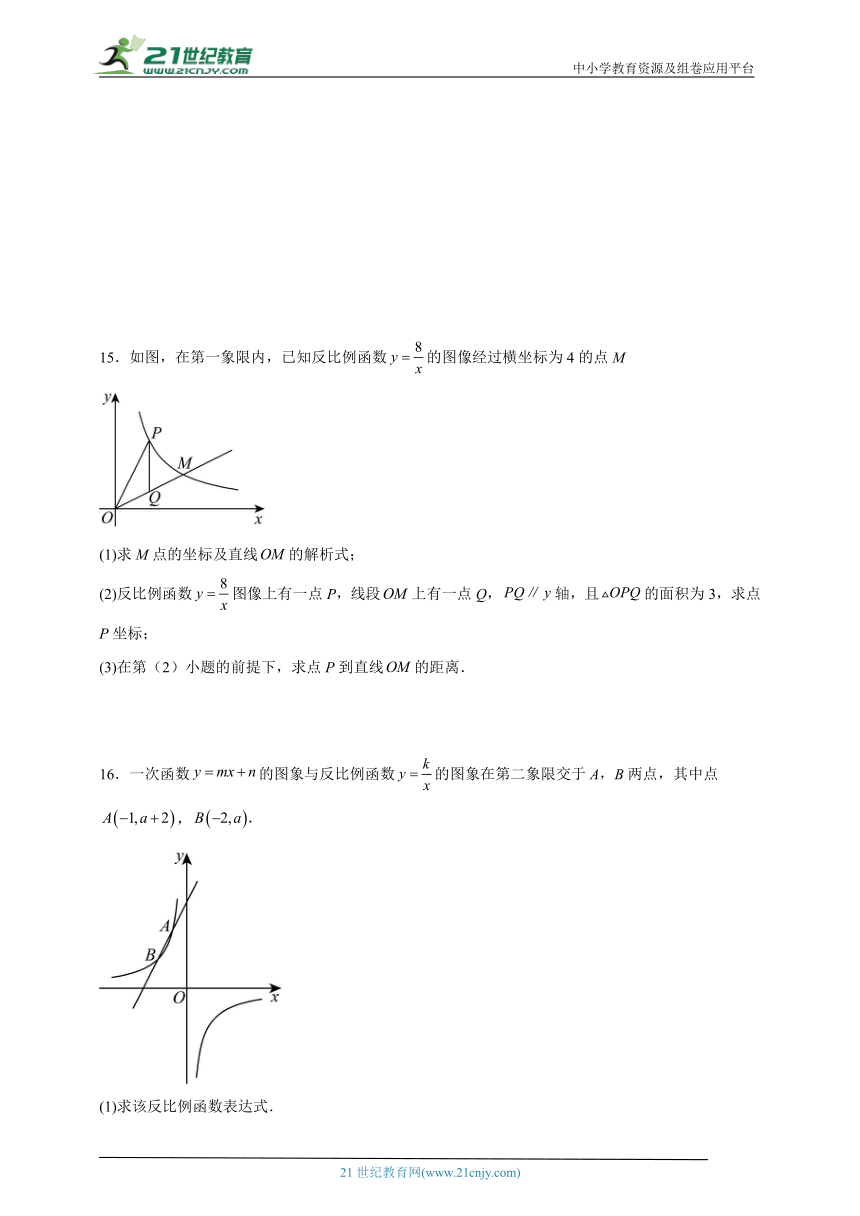
15.如图,在第一象限内,已知反比例函数的图像经过横坐标为4的点M
(1)求M点的坐标及直线的解析式;
(2)反比例函数图像上有一点P,线段上有一点Q,轴,且的面积为3,求点P坐标;
(3)在第(2)小题的前提下,求点P到直线的距离.
16.一次函数的图象与反比例函数的图象在第二象限交于A,B两点,其中点,
(1)求该反比例函数表达式.
(2)若把一次函数的图象向下平移b个单位长度,使之与反比例函数的图象只有一个交点,求b的值.
17.大约在两千四五百年前,如图1,墨子和他的学生做了世界上第1个小孔成像的实验,并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.如图2,根据小孔成像的科学原理,当像距(小孔到像的距离)和物高(蜡烛火焰高度)不变时,火焰的像高(单位:cm)是物距(小孔到蜡烛的距离)(单位:)的反比例函数.当时,.
(1)求关于的函数表达式.
(2)若物距(小孔到蜡烛的距离)为,求火焰的像高.
18.如图,在矩形中,,,点P为边上的一个动点,设,点M为射线上的一个动点,且,连接和,记的面积为,的面积为.
(1)请直接写出,分别关于x的函数表达式,并注明自变量x的取值范围;
(2)在给定的平面直角坐标系中画出函数,的图象;请分别写出函数,的一条性质;
(3)结合函数图象,直接写出时x的取值范围.(近似值保留一位小数,误差不超过)
19.如图为某公园“水上滑梯”的侧面图,建立如图所示的平面直角坐标系,其中段可看成是反比例函数图象的一段,为水面,矩形为向上攀爬的梯子,每节梯子高0.3米,宽1米,其中点A,E,D均在坐标轴上,且轴.
(1)①求k的值;
②求出口C点到的距离的长;
(2)若滑梯上有一个小球Q,要求Q到水面的距离不高于1.5米,则Q到的距离至少是多少米?
《第26章反比例函数章末精选题练习-2024-2025学年数学九年级下册人教版》参考答案
题号 1 2 3 4 5 6
答案 B C A C A C
1.B
【分析】根据三点,,都在反比例函数的图象上,得,判定函数图象在每个象限内,y随x的增大而增大,结合,得解答即可.本题考查了反比例函数图象的性质,熟练掌握性质是解题的关键.
【详解】解:三点,,都在反比例函数的图象上,
且,
∴函数图象在每个象限内,y随x的增大而增大,
根据,
∴,
故选:B.
2.C
【分析】本题考查了反比例函数的实际应用.将已知点的坐标代入到反比例函数的一般形式中即可求得其解析式;代入求得压强即可,解题的关键是根据图象建立函数关系式,并会运用函数式解答题目的问题.
【详解】解:设表达式为,
图象经过点,
,
所以表达式为;
当时,(千帕).
故选:C.
3.A
【分析】本题考查了反比例函数的图象与性质,反比例函数(k是常数,)的图象是双曲线,当,反比例函数图象的两个分支在第一、三象限;当,反比例函数图象的两个分支在第二、四象限.
【详解】解:∵比例函数的图象位于第一、三象限,
∴,
∴.
故选A.
4.C
【分析】本题考查了反比例函数图象:反比例函数()为双曲线,当时,图象分布在第一、三象限;当时,图象分布在第二、四象限.也考查了一次函数图象.根据一次函数和反比例函数的性质即可判断.
【详解】解:当时,一次函数1图象经过第一、二、三象限,反比例函数图象在第一、三象限,所以BD选项错误;C选项正确;
当时,一次函数图象经过第一、二、四象限,反比例函数图象在第二、四象限,所以A选项错误,
故选:C.
5.A
【分析】本题考查了反比例函数比例系数的几何意义,从反比例函数图象上任意一点向轴和轴作垂线,垂线与坐标轴所围成的矩形面积为;
根据反比例函数的图象关于原点中心对称得到点和点关于原点中心对称,则,得到,根据反比例函数系数的几何意义即可得到.
【详解】解:直线与双曲线交于,两点,
点和点关于原点中心对称,
,
,
,
,
;
反比例函数图象在第二、四象限,
,
,
故选:A .
6.C
【分析】本题考查了待定系数法求函数解析式,一次函数与反比例函数的交点问题,先利用待定系数法求出一次函数与反比例函数的解析式,进而求出点坐标,再结合图象解答即可求解,掌握数形结合思想是解题的关键.
【详解】解:把代入得,,
∴,
∴一次函数为,
把代入得,,
∴,
∴反比例函数为,
由,解得或,
∴,
由图象可得,当或时,,
故选:.
7.
【分析】本题主要考查了反比例函数图象的性质,
根据反比例函数的性质可知,求出解集即可.
【详解】解:∵反比例函数的图象的一支位于第二象限,
∴,
解得.
故答案为:.
8.4
【分析】本题考查了反比例函数的应用,根据图象的点在反比例函数上,求出该函数解析式为,结合该工程队每天最多建设0.5亩,得出,解得,即可作答.
【详解】解:依题意,先设该函数解析式为,
∵点在反比例函数上,
∴,
解得,
∴该函数解析式为,
∵该工程队每天最多建设0.5亩,
得出,
解得,
故答案为:4
9.
【分析】设,求解,过作轴于,过作轴于,证明,可得,可得,再进一步求解即可.
【详解】解:∵直线l:与 反 比 例 函 数的 图 象 交 于 点A, 与 x 轴交于点B,
设,
当时,则,
∴,
过作轴于,过作轴于,
∴,
∴,
∴,
∵,
∴,
∴,,
∴,
∴,
∵在上,
∴,
解得:(舍去),,
∴,
∴,
故答案为:
【点睛】本题考查的是旋转的性质,全等三角形的判定与性质,反比例函数与一次函数的综合应用,一元二次方程的解法,作出合适的辅助线是解本题的关键.
10.
【分析】本题考查的是正方形的性质,全等三角形的判定与性质,反比例函数的性质,由题意设,如图,过作轴于,过作轴于,证明,可得,再进一步解答即可.
【详解】解:由题意设,
如图,过作轴于,过作轴于,
∵正方形,
∴,,
∴,
∴,
∴,,
∴,
∴,
∴,
故答案为:
11.
【分析】本题主要考查了反比例函数的应用,矩形的性质,根据题意利用待定系数法求反比例函数解析式是解题的关键.设的解析式为,根据轴垂直平分,得到,结合的长度,得到点坐标,利用待定系数法从而得到的解析式,再由的长度得到点的横坐标为8,代入解析式得到点的纵坐标,即可求得整个冷却塔高度.
【详解】解:根据题意,设的解析式为,
四边形是矩形,
,,
轴垂直平分,,
,
,
,
,
解得:,
的解析式为,
,
点的横坐标为,
,
整个冷却塔高度为.
故答案为:.
12.
【分析】本题考查待定系数法求反比例函数解析式、等腰三角形的判定与性质、坐标与图形,正确求得点A坐标是解答的关键.过A作轴于D,根据坐标与图形性质和三角形的面积公式求得,利用等腰三角形的判定与性质求得,进而求得 ,然后利用待定系数法求解即可.
【详解】解:过A作轴于D,如图,
∵点B的坐标为,
∴,
∵,
∴,
∵,,
∴,
∴,
∴,
∴,
设这个反比例函数的表达式是,
∵这个反比例函数的图象经过点A,
∴,
∴这个反比例函数的表达式是,
故答案为:.
13.(1);
(2)
【分析】本题考查利用待定系数法求函数解析式,一次函数与反比例函数综合,掌握利用待定系数法求函数解析式和数形结合的思想是解题关键.
(1)利用待定系数法求解即可;
(2)先求出点C的坐标,从而可求出,进而可求出,最后根据三角形面积公式求解即可.
【详解】(1)解:把点代入直线得,
解得:,
一次函数的解析式为;
把点代入得,
,
∴反比例函数的解析式为;
(2)解:把代入,得:,
∴点的坐标为,
.
,
,
.
,
∴点的纵坐标为,则,
解得,
点的坐标为.
14.(1)
(2)直线OB的函数表达式为
(3)的面积为18
【分析】本题主要考查了反比例函数和一次函数的综合,求一次函数和反比例函数解析式,三角形面积的计算,解题的关键是数形结合熟练掌握待定系数法.
(1)根据中点坐标求出点A的坐标,再代入反比例函数解析式求出k的值即可;
(2)根据点B在反比例函数的图象上,先求出,再由待定系数法求解函数解析式;
(3)过点A作于点N,轴于点,由于轴,则四边形是矩形,求出的面积,根据三角形中线等分面积即可求解.
【详解】(1)解:∵点为,是的中点,
∴点为,
∴
∴反比例函数解析式为:,
(2)解:设点B坐标为
∵点B在反比例函数的图象上,
∴,
∴,
∴
设直线的函数表达式为,
∵点在直线上,
∴,
∴,
∴直线的函数表达式为;
(3)解:过点A作于点N,轴于点,由于轴,则四边形是矩形,
∵点为,点为,
∴,
∵,点
∴,
∴,
∵,
∴,
∴.
15.(1),
(2)
(3)
【分析】本题考查了一次函数与反比例函数综合;
(1)把代入得;设直线的解析式为把代入即可求解;
(2)设,则,,推出,即可求解;
(3)由题意得;,设点到直线的距离为h,根据,即可求解;
【详解】(1)解:把代入得:,
∴
设直线的解析式为
把代入得:,
解得:,
∴直线的解析式为:
(2)解:∵点P在上,点Q在线段上,轴,
∴设,则,
∴,
∴
即:,
解得:或(舍去)
∴;
(3)解:∵
∴;
∴,
设点P到直线的距离为
∴,
∴;
∴点P到直线的距离为
16.(1)反比例函数解析式为:;
(2)或
【分析】本题考查了一次函数与反比例函数的交点问题,熟练掌握交点坐标满足两个函数解析式是关键.
(1)待定系数法求出反比例函数解析式即可;
(2)先求出一次函数解析式,再按照平移法则得到平移后的解析式,与反比例函数解析式联立得到一元二次方程,根据根的判别式求出b值即可.
【详解】(1)解:点,都在反比例函数图象上,
,
解得,
,,
,
反比例函数解析式为:;
(2)解:,在一次函数的图象上,
,解得,
一次函数解析式为,
把一次函数的图象向下平移b个单位长度,
平移后的直线解析式为,
令,整理得:,
平移后的直线与反比例函数的图象只有一个交点,
,
解得或
17.(1)
(2)
【分析】本题考查了反比例函数的应用;
(1)利用待定系数法进行计算,即可解答;
(2)把代入解析式中进行计算,即可解答;
【详解】(1)解:设与的函数表达式为:,
把,代入中得:,
解得:,
∴关于的函数表达式为:;
(2)解:把代入中得:,
∴火焰的像高为.
18.(1),
(2)见解析
(3)
【分析】本题主要考查了矩形的性质、三角形的面积、一次函数和反比例函数图象的性质等知识点,掌握数形结合思想是解本题的关键.
(1)根据三角形的面积公式结合矩形的性质即可解答;
(2)正确画函数的图象,再根据图象写出性质即可;
(3)根据函数图象由的图象在上边时对应的x的值即可.
【详解】(1)解:∵四边形是矩形,
∴,
∴,.
(2)解:
函数的一条性质是∶ 随x的增大而增大(答案不唯一);
函数的一条性质是: 随x的增大而减小(答案不唯一).
(3)解:由函数图象得:当时x的取值范围是:.
19.(1) 米
(2)米
【分析】(1)①先求出点的坐标,然后将其代入反比例函数解析式,得到关于的一元一次方程,解方程即可求出的值;②先求出点的纵坐标,然后将其代入反比例函数解析式,得到关于的分式方程,解方程即可求出的值,进而得出点的坐标,于是即可求出的长;
(2)当时,,解方程即可求出此时的值,由于,因而随x的增大而减小,由此可知,当时,米,进而可求出此时点到的距离.
【详解】(1)解:①由题意可得:
(米),(米),
点的坐标为,
点在反比例函数的图象上,
,
解得:;
②(米),
点的纵坐标为,
由得:反比例函数的解析式为,
当时,,
解得:,
经检验,是原分式方程的解,
点的坐标为,
(米);
(2)解:当时,,
解得:,
经检验,是原分式方程的解,
,
随x的增大而减小,
当时,(米),
(米),
点到的距离至少是米.
【点睛】本题主要考查了求反比例函数解析式,解一元一次方程,解分式方程,反比例函数的性质等知识点,熟练掌握待定系数法求反比例函数解析式及反比例函数的性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第26章反比例函数章末精选题练习-2024-2025学年数学九年级下册人教版
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知点,,在反比例函数的图象上,下列结论正确的是( )
A. B. C. D.
2.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压(千帕)是气体体积(立方米)的反比例函数,其图像如图所示(千帕是一种压强单位),当气球的体积是0.8立方米时,气球内的气压是( )千帕
A.100 B.110 C.120 D.130
3.已知反比例函数的图象位于第一、三象限,则的取值范围是( )
A. B. C. D.
4.一次函数(k为常数,且)和反比例函数在同一平面直角坐标系中的图象可能是( ).
A. B.
C. D.
5.如图,直线与双曲线交于,两点,过点作轴,垂足为点,连接,若,则的值为( )
A. B. C. D.
6.如图,直线与双曲线交于点和点,则不等式的解集是( )
A.或 B.
C.或 D.或
二、填空题
7.已知反比例函数的图象的一支位于第二象限,则常数m的取值范围是 .
8.负责鱼菜共生系统建设的工程队平均每天的工作量(亩/天)与完成建设所需的时间(天)之间的函数图象如图所示,若该工程队每天最多建设0.5亩,则该工程队完成全部鱼菜共生系统的建设最快需要 天.
9.如图,直线l:与 反 比 例 函 数的 图 象 交 于 点A, 与 x 轴交于点B, 将 线 段 绕 点B逆时针旋转至线段,若点C恰好也在反比例函数图象上,则k的值为 ·
10.如图,在平面直角坐标系中,正方形的顶点与坐标原点重合,点分别在反比例函数与的图象上,则的值为 .
11.火力发电厂的大烟囱并不是我们所理解的排放废气的烟囱,它的专业名字叫双曲线冷却塔,从这里冒出的烟雾其实只是水蒸气,它的纵截面是如图所示的轴对称图形,是一个矩形,若以所在直线为轴,的垂直平分线为轴建立如图所示的平面直角坐标系,、分别是两个反比例函数图像的一部分,已知,,上口宽,则整个冷却塔高度为 m.
12.如图,在中,边与x轴交于点C,且,某一反比例函数的图象经过点A,若点B的坐标为,,则这个反比例函数的表达式是 .
三、解答题
13.如图,在平面直角坐标系中,一次函数与反比例函数的图象在第一象限交于点A,与x轴相交于点C.已知点A的坐标分别为.
(1)求一次函数和反比例函数的解析式;
(2)点P为反比例函数图象上的任意一点,若,求点P的坐标.
14.如图,反比例函数()的图象经过A,B两点,连接,,过点B作轴,垂足为点D,交于点E,若E为的中点,且点E坐标为.
(1)求k的值;
(2)连接,求直线的函数表达式;
(3)求的面积.
15.如图,在第一象限内,已知反比例函数的图像经过横坐标为4的点M
(1)求M点的坐标及直线的解析式;
(2)反比例函数图像上有一点P,线段上有一点Q,轴,且的面积为3,求点P坐标;
(3)在第(2)小题的前提下,求点P到直线的距离.
16.一次函数的图象与反比例函数的图象在第二象限交于A,B两点,其中点,
(1)求该反比例函数表达式.
(2)若把一次函数的图象向下平移b个单位长度,使之与反比例函数的图象只有一个交点,求b的值.
17.大约在两千四五百年前,如图1,墨子和他的学生做了世界上第1个小孔成像的实验,并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.如图2,根据小孔成像的科学原理,当像距(小孔到像的距离)和物高(蜡烛火焰高度)不变时,火焰的像高(单位:cm)是物距(小孔到蜡烛的距离)(单位:)的反比例函数.当时,.
(1)求关于的函数表达式.
(2)若物距(小孔到蜡烛的距离)为,求火焰的像高.
18.如图,在矩形中,,,点P为边上的一个动点,设,点M为射线上的一个动点,且,连接和,记的面积为,的面积为.
(1)请直接写出,分别关于x的函数表达式,并注明自变量x的取值范围;
(2)在给定的平面直角坐标系中画出函数,的图象;请分别写出函数,的一条性质;
(3)结合函数图象,直接写出时x的取值范围.(近似值保留一位小数,误差不超过)
19.如图为某公园“水上滑梯”的侧面图,建立如图所示的平面直角坐标系,其中段可看成是反比例函数图象的一段,为水面,矩形为向上攀爬的梯子,每节梯子高0.3米,宽1米,其中点A,E,D均在坐标轴上,且轴.
(1)①求k的值;
②求出口C点到的距离的长;
(2)若滑梯上有一个小球Q,要求Q到水面的距离不高于1.5米,则Q到的距离至少是多少米?
《第26章反比例函数章末精选题练习-2024-2025学年数学九年级下册人教版》参考答案
题号 1 2 3 4 5 6
答案 B C A C A C
1.B
【分析】根据三点,,都在反比例函数的图象上,得,判定函数图象在每个象限内,y随x的增大而增大,结合,得解答即可.本题考查了反比例函数图象的性质,熟练掌握性质是解题的关键.
【详解】解:三点,,都在反比例函数的图象上,
且,
∴函数图象在每个象限内,y随x的增大而增大,
根据,
∴,
故选:B.
2.C
【分析】本题考查了反比例函数的实际应用.将已知点的坐标代入到反比例函数的一般形式中即可求得其解析式;代入求得压强即可,解题的关键是根据图象建立函数关系式,并会运用函数式解答题目的问题.
【详解】解:设表达式为,
图象经过点,
,
所以表达式为;
当时,(千帕).
故选:C.
3.A
【分析】本题考查了反比例函数的图象与性质,反比例函数(k是常数,)的图象是双曲线,当,反比例函数图象的两个分支在第一、三象限;当,反比例函数图象的两个分支在第二、四象限.
【详解】解:∵比例函数的图象位于第一、三象限,
∴,
∴.
故选A.
4.C
【分析】本题考查了反比例函数图象:反比例函数()为双曲线,当时,图象分布在第一、三象限;当时,图象分布在第二、四象限.也考查了一次函数图象.根据一次函数和反比例函数的性质即可判断.
【详解】解:当时,一次函数1图象经过第一、二、三象限,反比例函数图象在第一、三象限,所以BD选项错误;C选项正确;
当时,一次函数图象经过第一、二、四象限,反比例函数图象在第二、四象限,所以A选项错误,
故选:C.
5.A
【分析】本题考查了反比例函数比例系数的几何意义,从反比例函数图象上任意一点向轴和轴作垂线,垂线与坐标轴所围成的矩形面积为;
根据反比例函数的图象关于原点中心对称得到点和点关于原点中心对称,则,得到,根据反比例函数系数的几何意义即可得到.
【详解】解:直线与双曲线交于,两点,
点和点关于原点中心对称,
,
,
,
,
;
反比例函数图象在第二、四象限,
,
,
故选:A .
6.C
【分析】本题考查了待定系数法求函数解析式,一次函数与反比例函数的交点问题,先利用待定系数法求出一次函数与反比例函数的解析式,进而求出点坐标,再结合图象解答即可求解,掌握数形结合思想是解题的关键.
【详解】解:把代入得,,
∴,
∴一次函数为,
把代入得,,
∴,
∴反比例函数为,
由,解得或,
∴,
由图象可得,当或时,,
故选:.
7.
【分析】本题主要考查了反比例函数图象的性质,
根据反比例函数的性质可知,求出解集即可.
【详解】解:∵反比例函数的图象的一支位于第二象限,
∴,
解得.
故答案为:.
8.4
【分析】本题考查了反比例函数的应用,根据图象的点在反比例函数上,求出该函数解析式为,结合该工程队每天最多建设0.5亩,得出,解得,即可作答.
【详解】解:依题意,先设该函数解析式为,
∵点在反比例函数上,
∴,
解得,
∴该函数解析式为,
∵该工程队每天最多建设0.5亩,
得出,
解得,
故答案为:4
9.
【分析】设,求解,过作轴于,过作轴于,证明,可得,可得,再进一步求解即可.
【详解】解:∵直线l:与 反 比 例 函 数的 图 象 交 于 点A, 与 x 轴交于点B,
设,
当时,则,
∴,
过作轴于,过作轴于,
∴,
∴,
∴,
∵,
∴,
∴,,
∴,
∴,
∵在上,
∴,
解得:(舍去),,
∴,
∴,
故答案为:
【点睛】本题考查的是旋转的性质,全等三角形的判定与性质,反比例函数与一次函数的综合应用,一元二次方程的解法,作出合适的辅助线是解本题的关键.
10.
【分析】本题考查的是正方形的性质,全等三角形的判定与性质,反比例函数的性质,由题意设,如图,过作轴于,过作轴于,证明,可得,再进一步解答即可.
【详解】解:由题意设,
如图,过作轴于,过作轴于,
∵正方形,
∴,,
∴,
∴,
∴,,
∴,
∴,
∴,
故答案为:
11.
【分析】本题主要考查了反比例函数的应用,矩形的性质,根据题意利用待定系数法求反比例函数解析式是解题的关键.设的解析式为,根据轴垂直平分,得到,结合的长度,得到点坐标,利用待定系数法从而得到的解析式,再由的长度得到点的横坐标为8,代入解析式得到点的纵坐标,即可求得整个冷却塔高度.
【详解】解:根据题意,设的解析式为,
四边形是矩形,
,,
轴垂直平分,,
,
,
,
,
解得:,
的解析式为,
,
点的横坐标为,
,
整个冷却塔高度为.
故答案为:.
12.
【分析】本题考查待定系数法求反比例函数解析式、等腰三角形的判定与性质、坐标与图形,正确求得点A坐标是解答的关键.过A作轴于D,根据坐标与图形性质和三角形的面积公式求得,利用等腰三角形的判定与性质求得,进而求得 ,然后利用待定系数法求解即可.
【详解】解:过A作轴于D,如图,
∵点B的坐标为,
∴,
∵,
∴,
∵,,
∴,
∴,
∴,
∴,
设这个反比例函数的表达式是,
∵这个反比例函数的图象经过点A,
∴,
∴这个反比例函数的表达式是,
故答案为:.
13.(1);
(2)
【分析】本题考查利用待定系数法求函数解析式,一次函数与反比例函数综合,掌握利用待定系数法求函数解析式和数形结合的思想是解题关键.
(1)利用待定系数法求解即可;
(2)先求出点C的坐标,从而可求出,进而可求出,最后根据三角形面积公式求解即可.
【详解】(1)解:把点代入直线得,
解得:,
一次函数的解析式为;
把点代入得,
,
∴反比例函数的解析式为;
(2)解:把代入,得:,
∴点的坐标为,
.
,
,
.
,
∴点的纵坐标为,则,
解得,
点的坐标为.
14.(1)
(2)直线OB的函数表达式为
(3)的面积为18
【分析】本题主要考查了反比例函数和一次函数的综合,求一次函数和反比例函数解析式,三角形面积的计算,解题的关键是数形结合熟练掌握待定系数法.
(1)根据中点坐标求出点A的坐标,再代入反比例函数解析式求出k的值即可;
(2)根据点B在反比例函数的图象上,先求出,再由待定系数法求解函数解析式;
(3)过点A作于点N,轴于点,由于轴,则四边形是矩形,求出的面积,根据三角形中线等分面积即可求解.
【详解】(1)解:∵点为,是的中点,
∴点为,
∴
∴反比例函数解析式为:,
(2)解:设点B坐标为
∵点B在反比例函数的图象上,
∴,
∴,
∴
设直线的函数表达式为,
∵点在直线上,
∴,
∴,
∴直线的函数表达式为;
(3)解:过点A作于点N,轴于点,由于轴,则四边形是矩形,
∵点为,点为,
∴,
∵,点
∴,
∴,
∵,
∴,
∴.
15.(1),
(2)
(3)
【分析】本题考查了一次函数与反比例函数综合;
(1)把代入得;设直线的解析式为把代入即可求解;
(2)设,则,,推出,即可求解;
(3)由题意得;,设点到直线的距离为h,根据,即可求解;
【详解】(1)解:把代入得:,
∴
设直线的解析式为
把代入得:,
解得:,
∴直线的解析式为:
(2)解:∵点P在上,点Q在线段上,轴,
∴设,则,
∴,
∴
即:,
解得:或(舍去)
∴;
(3)解:∵
∴;
∴,
设点P到直线的距离为
∴,
∴;
∴点P到直线的距离为
16.(1)反比例函数解析式为:;
(2)或
【分析】本题考查了一次函数与反比例函数的交点问题,熟练掌握交点坐标满足两个函数解析式是关键.
(1)待定系数法求出反比例函数解析式即可;
(2)先求出一次函数解析式,再按照平移法则得到平移后的解析式,与反比例函数解析式联立得到一元二次方程,根据根的判别式求出b值即可.
【详解】(1)解:点,都在反比例函数图象上,
,
解得,
,,
,
反比例函数解析式为:;
(2)解:,在一次函数的图象上,
,解得,
一次函数解析式为,
把一次函数的图象向下平移b个单位长度,
平移后的直线解析式为,
令,整理得:,
平移后的直线与反比例函数的图象只有一个交点,
,
解得或
17.(1)
(2)
【分析】本题考查了反比例函数的应用;
(1)利用待定系数法进行计算,即可解答;
(2)把代入解析式中进行计算,即可解答;
【详解】(1)解:设与的函数表达式为:,
把,代入中得:,
解得:,
∴关于的函数表达式为:;
(2)解:把代入中得:,
∴火焰的像高为.
18.(1),
(2)见解析
(3)
【分析】本题主要考查了矩形的性质、三角形的面积、一次函数和反比例函数图象的性质等知识点,掌握数形结合思想是解本题的关键.
(1)根据三角形的面积公式结合矩形的性质即可解答;
(2)正确画函数的图象,再根据图象写出性质即可;
(3)根据函数图象由的图象在上边时对应的x的值即可.
【详解】(1)解:∵四边形是矩形,
∴,
∴,.
(2)解:
函数的一条性质是∶ 随x的增大而增大(答案不唯一);
函数的一条性质是: 随x的增大而减小(答案不唯一).
(3)解:由函数图象得:当时x的取值范围是:.
19.(1) 米
(2)米
【分析】(1)①先求出点的坐标,然后将其代入反比例函数解析式,得到关于的一元一次方程,解方程即可求出的值;②先求出点的纵坐标,然后将其代入反比例函数解析式,得到关于的分式方程,解方程即可求出的值,进而得出点的坐标,于是即可求出的长;
(2)当时,,解方程即可求出此时的值,由于,因而随x的增大而减小,由此可知,当时,米,进而可求出此时点到的距离.
【详解】(1)解:①由题意可得:
(米),(米),
点的坐标为,
点在反比例函数的图象上,
,
解得:;
②(米),
点的纵坐标为,
由得:反比例函数的解析式为,
当时,,
解得:,
经检验,是原分式方程的解,
点的坐标为,
(米);
(2)解:当时,,
解得:,
经检验,是原分式方程的解,
,
随x的增大而减小,
当时,(米),
(米),
点到的距离至少是米.
【点睛】本题主要考查了求反比例函数解析式,解一元一次方程,解分式方程,反比例函数的性质等知识点,熟练掌握待定系数法求反比例函数解析式及反比例函数的性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
