第五章 圆 7 切线长定理(含答案)
文档属性
| 名称 | 第五章 圆 7 切线长定理(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 489.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-01 13:25:48 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第五章 圆
7 切线长定理
轻松过关
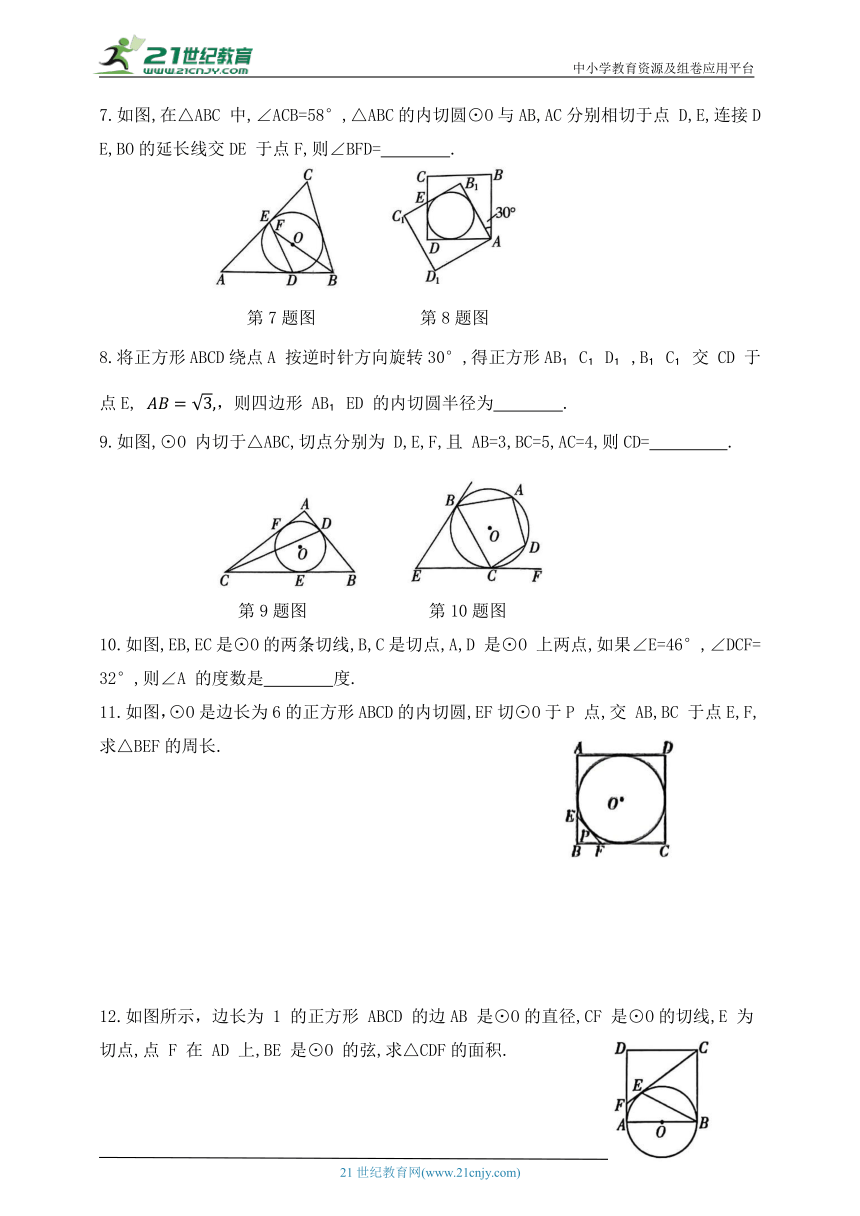
1.如图,PA,PB,CD分别与⊙O相切于点A,B,E,∠APB=54°,则∠COD= ( )
A.36° B.63° C.126° D.46°
第1题图 第2题图
2.如图,EA,ED是⊙O的切线,切点为A,D,点B,C在⊙O上,若∠BAE+∠BCD=236°,则∠E= ( )
A.56° B.60° C.68° D.70°
3.如图,直线 AB,BC,CD 分别与⊙O 相切于E,F,G,且 AB∥CD,若OB=6,OC=8,则BE+CG的长等于 ( )
A.13 B.12 C.11 D.10
第3题图 第4题图
4.如图,四边形 ABCD 外切于⊙O,且 AB=10,CD=15,则四边形ABCD的周长为( )
A.60 B.55 C.45 D.50
5.如图,在 Rt△ABC中,∠C=90°,AC=4,BC=3,以 BC上一点O 为圆心作⊙O与AB 相切于点 E,与AC相切于点C,与 BC的另一交点为点 D,则线段 BD 的长为( )
A.1 B. C. D.
6.如图,在△ABC中,∠A=60°,BC=6,它的周长为16.若⊙O与 BC,AC,AB 三边分别相切于E,F,D点,则 DF的长为 ( )
A.2 B.3 C.4 D.6
7.如图,在△ABC 中,∠ACB=58°,△ABC的内切圆⊙O与AB,AC分别相切于点 D,E,连接DE,BO的延长线交DE 于点F,则∠BFD= .
第7题图 第8题图
8.将正方形ABCD绕点A 按逆时针方向旋转30°,得正方形AB C D ,B C 交 CD 于点E, ,则四边形 AB ED 的内切圆半径为 .
9.如图,⊙O 内切于△ABC,切点分别为 D,E,F,且 AB=3,BC=5,AC=4,则CD= .
第9题图 第10题图
10.如图,EB,EC是⊙O的两条切线,B,C是切点,A,D 是⊙O 上两点,如果∠E=46°,∠DCF=32°,则∠A 的度数是 度.
11.如图,⊙O是边长为6的正方形ABCD的内切圆,EF切⊙O于P 点,交 AB,BC 于点E,F,求△BEF的周长.
12.如图所示,边长为 1 的正方形 ABCD 的边AB 是⊙O的直径,CF 是⊙O的切线,E 为切点,点 F 在 AD 上,BE 是⊙O 的弦,求△CDF的面积.
13.如图所示,AB是⊙O的直径,过⊙O外一点 P 作⊙O 的两条切线 PC,PD,切点分别为C,D,连接OP,CD.
(1)求证:OP⊥CD;
(2)连接AD,BC,若∠DAB=50°,∠CBA=70°,OA=2,求OP的长.
14.如图所示,在△ABC 中,∠C=90°,AC+BC=8,点O是斜边AB 上一点,以点O为圆心的⊙O分别与AC,BC 相切于点 D,E.当AC=2时,求⊙O的半径.
15.已知:如图,在 Rt△ABC 中,∠C=90°,⊙O与△ABC的三边分别切于点D,E,F.
(1)连接AO,BO,求∠AOB 的度数;
(2)连接BD,若 求tan∠ABD的值.
快乐拓展
16.刘徽(今山东滨州人)是魏晋时期我国伟大的数学家,中国古典数学理论的奠基者之一,被誉为“世界古代数学泰斗”.刘徽在注释《九章算术》时十分重视一题多解,其中最典型的是勾股容方和勾股容圆公式的推导,他给出了内切圆直径的多种表达形式.如图,Rt△ABC 中,∠C=90°,AB,BC,CA的长分别为c,a,b.则可以用含 c,a,b 的式子表示出△ABC 的内切圆直径d,下列表达式错误的是 ( )
17.如图,AB为⊙O直径,PA,PC分别与⊙O相切于点A,C,PQ⊥PA,PQ交OC 的延长线于点Q.
(1)求证:OQ=PQ;
(2)连接 BC并延长交 PQ于点 D,若 PA=AB,且CQ=6,求 BD的长.
参考答案
1. B 2. C 3. D 4. D 5. C 6. A
7.29° 9. 10.99
11.解:设⊙O切AB 于点M,切 BC于点N,连接OM,ON,OP,则∠OMB=∠ONB=90°,
∵四边形ABCD 是正方形,∴∠B=90°.∴四边形 MBNO是矩形,
∵ON=OM,∴四边形 MBNO是正方形.
∵⊙O是边长为6的正方形ABCD的内切圆,
6=3.
由切线长定理得 EM=EP,PF=FN,
∴△BEF的周长为BF+EF+BE=BF+PF+PE+BE= BF+FN+EM+BE=BN+BM=3+3=6.
12.解:设AF=x,
∵四边形 ABCD是正方形,∴∠DAB=∠D=∠ABC=90°.
∴DA⊥AB,BC⊥AB.∴AD,BC是⊙O的切线.
∵CF是⊙O的切线,E为切点,∴EF=AF=x,CE=BC=1.
∴FD=1-x,CF=CE+EF=1+x.
在Rt△CDF中,由勾股定理,得CF =CD +DF ,
即 解得
13.解:(1)证明:如图所示,连接OC,OD,则OC=OD.
∵PD,PC是⊙O的切线,∴PD=PC,
∴OP 垂直平分CD,∴OP⊥CD;
(2)如图所示,
∵OA=OD=OC=OB=2,∴∠ADO=∠DAO=50°,∠BCO=∠CBO=70°.
∴∠AOD = 80°,∠BOC =40°.∴∠COD=60°.
∵OD=OC,∴△COD是等边三角形.
∵OP⊥CD,∴∠DOP=∠COP=30°,在 Rt△ODP中
14.解:如图所示,连接OE,OD.在△ABC中,∠C=90°,AC+BC=8,
∵AC=2,∴BC=6.
∵以O为圆心的⊙O分别与AC,BC相切于点D,E,∴四边形OECD 是正方形, 解得 ∴圆的半径为
15.解:(1)如图1,连接DO,EO,FO,
∵AC,BC,AB均为⊙O的切线,
∴AF=AD,BF=BE,CE=CD,∠ODC=90°,∠OEC=90°.
∵∠C=90°,∴∠DOE=90°.
在△ADO与△AFO中, ∴△ADO≌△AFO(SAS).
∴∠AOF=∠AOD.同理,得∠BOF=∠BOE,
(2)过点 D 作 DM⊥AB于点M,如图2,
∴设DC=1,则 BC=4.∴CE=CD=1,BF=BE=3.
设AD=AF=x,则AC=1+x,AB=3+x,
在 Rt△ABC中, 解得x=2,
∴AD=AF=2,AB=5,
∵△ADM∽△ABC,
16. D
17.解:(1)证明:连接OP.
∵PA,PC分别与⊙O相切于点A,C,∴PA=PC,OA⊥PA,
∵OA=OC,OP=OP,∴△OPA≌△OPC(SSS),∴∠AOP=∠POC,
∵QP⊥PA,∴QP∥BA,∴∠QPO=∠AOP,
∴∠QOP=∠QPO,∴OQ=PQ;
(2)设OA=r.∴AB=PA=2r,∴PC=2r.
∵OB=OC,∴∠B=∠OCB,
∵OB∥QD,∴∠QDC=∠B,
∵∠OCB=∠QCD,∴∠QCD=∠QDC,∴QC=QD=6,
∵QO=QP,∴OC=DP=r,
∵PC是⊙O的切线,∴OC⊥PC,∴∠OCP=∠PCQ=90°,
在 Rt△PCQ中,
解得r=4或0(舍去),
∵OB=PD,OB∥PD,∴四边形OBDP 是平行四边形,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 圆
7 切线长定理
轻松过关
1.如图,PA,PB,CD分别与⊙O相切于点A,B,E,∠APB=54°,则∠COD= ( )
A.36° B.63° C.126° D.46°
第1题图 第2题图
2.如图,EA,ED是⊙O的切线,切点为A,D,点B,C在⊙O上,若∠BAE+∠BCD=236°,则∠E= ( )
A.56° B.60° C.68° D.70°
3.如图,直线 AB,BC,CD 分别与⊙O 相切于E,F,G,且 AB∥CD,若OB=6,OC=8,则BE+CG的长等于 ( )
A.13 B.12 C.11 D.10
第3题图 第4题图
4.如图,四边形 ABCD 外切于⊙O,且 AB=10,CD=15,则四边形ABCD的周长为( )
A.60 B.55 C.45 D.50
5.如图,在 Rt△ABC中,∠C=90°,AC=4,BC=3,以 BC上一点O 为圆心作⊙O与AB 相切于点 E,与AC相切于点C,与 BC的另一交点为点 D,则线段 BD 的长为( )
A.1 B. C. D.
6.如图,在△ABC中,∠A=60°,BC=6,它的周长为16.若⊙O与 BC,AC,AB 三边分别相切于E,F,D点,则 DF的长为 ( )
A.2 B.3 C.4 D.6
7.如图,在△ABC 中,∠ACB=58°,△ABC的内切圆⊙O与AB,AC分别相切于点 D,E,连接DE,BO的延长线交DE 于点F,则∠BFD= .
第7题图 第8题图
8.将正方形ABCD绕点A 按逆时针方向旋转30°,得正方形AB C D ,B C 交 CD 于点E, ,则四边形 AB ED 的内切圆半径为 .
9.如图,⊙O 内切于△ABC,切点分别为 D,E,F,且 AB=3,BC=5,AC=4,则CD= .
第9题图 第10题图
10.如图,EB,EC是⊙O的两条切线,B,C是切点,A,D 是⊙O 上两点,如果∠E=46°,∠DCF=32°,则∠A 的度数是 度.
11.如图,⊙O是边长为6的正方形ABCD的内切圆,EF切⊙O于P 点,交 AB,BC 于点E,F,求△BEF的周长.
12.如图所示,边长为 1 的正方形 ABCD 的边AB 是⊙O的直径,CF 是⊙O的切线,E 为切点,点 F 在 AD 上,BE 是⊙O 的弦,求△CDF的面积.
13.如图所示,AB是⊙O的直径,过⊙O外一点 P 作⊙O 的两条切线 PC,PD,切点分别为C,D,连接OP,CD.
(1)求证:OP⊥CD;
(2)连接AD,BC,若∠DAB=50°,∠CBA=70°,OA=2,求OP的长.
14.如图所示,在△ABC 中,∠C=90°,AC+BC=8,点O是斜边AB 上一点,以点O为圆心的⊙O分别与AC,BC 相切于点 D,E.当AC=2时,求⊙O的半径.
15.已知:如图,在 Rt△ABC 中,∠C=90°,⊙O与△ABC的三边分别切于点D,E,F.
(1)连接AO,BO,求∠AOB 的度数;
(2)连接BD,若 求tan∠ABD的值.
快乐拓展
16.刘徽(今山东滨州人)是魏晋时期我国伟大的数学家,中国古典数学理论的奠基者之一,被誉为“世界古代数学泰斗”.刘徽在注释《九章算术》时十分重视一题多解,其中最典型的是勾股容方和勾股容圆公式的推导,他给出了内切圆直径的多种表达形式.如图,Rt△ABC 中,∠C=90°,AB,BC,CA的长分别为c,a,b.则可以用含 c,a,b 的式子表示出△ABC 的内切圆直径d,下列表达式错误的是 ( )
17.如图,AB为⊙O直径,PA,PC分别与⊙O相切于点A,C,PQ⊥PA,PQ交OC 的延长线于点Q.
(1)求证:OQ=PQ;
(2)连接 BC并延长交 PQ于点 D,若 PA=AB,且CQ=6,求 BD的长.
参考答案
1. B 2. C 3. D 4. D 5. C 6. A
7.29° 9. 10.99
11.解:设⊙O切AB 于点M,切 BC于点N,连接OM,ON,OP,则∠OMB=∠ONB=90°,
∵四边形ABCD 是正方形,∴∠B=90°.∴四边形 MBNO是矩形,
∵ON=OM,∴四边形 MBNO是正方形.
∵⊙O是边长为6的正方形ABCD的内切圆,
6=3.
由切线长定理得 EM=EP,PF=FN,
∴△BEF的周长为BF+EF+BE=BF+PF+PE+BE= BF+FN+EM+BE=BN+BM=3+3=6.
12.解:设AF=x,
∵四边形 ABCD是正方形,∴∠DAB=∠D=∠ABC=90°.
∴DA⊥AB,BC⊥AB.∴AD,BC是⊙O的切线.
∵CF是⊙O的切线,E为切点,∴EF=AF=x,CE=BC=1.
∴FD=1-x,CF=CE+EF=1+x.
在Rt△CDF中,由勾股定理,得CF =CD +DF ,
即 解得
13.解:(1)证明:如图所示,连接OC,OD,则OC=OD.
∵PD,PC是⊙O的切线,∴PD=PC,
∴OP 垂直平分CD,∴OP⊥CD;
(2)如图所示,
∵OA=OD=OC=OB=2,∴∠ADO=∠DAO=50°,∠BCO=∠CBO=70°.
∴∠AOD = 80°,∠BOC =40°.∴∠COD=60°.
∵OD=OC,∴△COD是等边三角形.
∵OP⊥CD,∴∠DOP=∠COP=30°,在 Rt△ODP中
14.解:如图所示,连接OE,OD.在△ABC中,∠C=90°,AC+BC=8,
∵AC=2,∴BC=6.
∵以O为圆心的⊙O分别与AC,BC相切于点D,E,∴四边形OECD 是正方形, 解得 ∴圆的半径为
15.解:(1)如图1,连接DO,EO,FO,
∵AC,BC,AB均为⊙O的切线,
∴AF=AD,BF=BE,CE=CD,∠ODC=90°,∠OEC=90°.
∵∠C=90°,∴∠DOE=90°.
在△ADO与△AFO中, ∴△ADO≌△AFO(SAS).
∴∠AOF=∠AOD.同理,得∠BOF=∠BOE,
(2)过点 D 作 DM⊥AB于点M,如图2,
∴设DC=1,则 BC=4.∴CE=CD=1,BF=BE=3.
设AD=AF=x,则AC=1+x,AB=3+x,
在 Rt△ABC中, 解得x=2,
∴AD=AF=2,AB=5,
∵△ADM∽△ABC,
16. D
17.解:(1)证明:连接OP.
∵PA,PC分别与⊙O相切于点A,C,∴PA=PC,OA⊥PA,
∵OA=OC,OP=OP,∴△OPA≌△OPC(SSS),∴∠AOP=∠POC,
∵QP⊥PA,∴QP∥BA,∴∠QPO=∠AOP,
∴∠QOP=∠QPO,∴OQ=PQ;
(2)设OA=r.∴AB=PA=2r,∴PC=2r.
∵OB=OC,∴∠B=∠OCB,
∵OB∥QD,∴∠QDC=∠B,
∵∠OCB=∠QCD,∴∠QCD=∠QDC,∴QC=QD=6,
∵QO=QP,∴OC=DP=r,
∵PC是⊙O的切线,∴OC⊥PC,∴∠OCP=∠PCQ=90°,
在 Rt△PCQ中,
解得r=4或0(舍去),
∵OB=PD,OB∥PD,∴四边形OBDP 是平行四边形,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
