第五章 圆 8 正多边形和圆(含答案)
文档属性
| 名称 | 第五章 圆 8 正多边形和圆(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 441.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-01 13:26:10 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第五章 圆
8 正多边形和圆
轻松过关
1.下列命题:①各角相等的多边形是正多边形 ②任何正多边形都有一个外接圆和一个内切圆,并且这两个圆是同心圆 ③正六边形的外接圆半径与边长相等 ④在正多边形中,中心角与正多边形的每个外角相等.其中,真命题的个数是
( )
A.4个 B.3个 C.2个 D.1个
2.如图,正三角形和正六边形都内接于⊙O,连接OC,则 ( )
A.90° B.100° C.110° D.120°
3.如图,点P ~P 是⊙O 的八等分点.若△P P P ,四边形 P P P P 的周长分别为a,b,则下列正确的是 ( )
大小无法比较
4.如图,⊙O与正五边形ABCDE的两边AE,CD相切于A,C两点,则∠AOC的度数是 ( )
A.144° B.130° C.129° D.108°
5.已知,正六边形 ABCDEF 的面积为 6,则正六边形的边长为 ( )
A.1 B. C.2 D.4
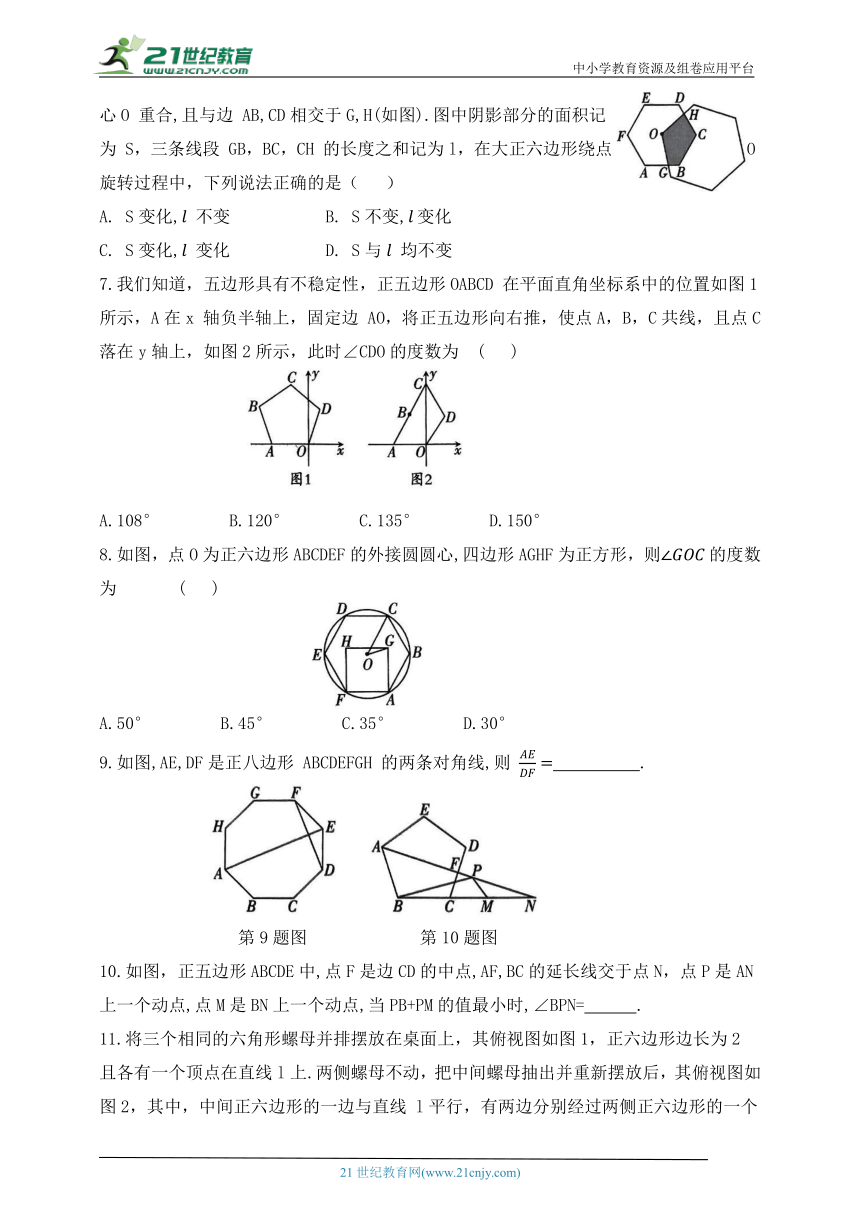
6.一个适当大的正六边形,它的一个顶点与一个边长为定值的小正六边形ABCDEF 的中心O 重合,且与边 AB,CD相交于G,H(如图).图中阴影部分的面积记为 S,三条线段 GB,BC,CH 的长度之和记为l,在大正六边形绕点O旋转过程中,下列说法正确的是( )
A. S变化, 不变 B. S不变,变化
C. S变化, 变化 D. S与 均不变
7.我们知道,五边形具有不稳定性,正五边形OABCD 在平面直角坐标系中的位置如图1所示,A在x 轴负半轴上,固定边 AO,将正五边形向右推,使点A,B,C共线,且点C落在y轴上,如图2所示,此时∠CDO的度数为 ( )
A.108° B.120° C.135° D.150°
8.如图,点O为正六边形ABCDEF的外接圆圆心,四边形AGHF为正方形,则的度数为 ( )
A.50° B.45° C.35° D.30°
9.如图,AE,DF是正八边形 ABCDEFGH 的两条对角线,则 .
第9题图 第10题图
10.如图,正五边形ABCDE中,点F是边CD的中点,AF,BC的延长线交于点N,点P是AN上一个动点,点M是BN上一个动点,当PB+PM的值最小时,∠BPN= .
11.将三个相同的六角形螺母并排摆放在桌面上,其俯视图如图1,正六边形边长为2 且各有一个顶点在直线l上.两侧螺母不动,把中间螺母抽出并重新摆放后,其俯视图如图2,其中,中间正六边形的一边与直线 l平行,有两边分别经过两侧正六边形的一个顶点.则图2中:
(1)∠α= 度;
(2)中间正六边形的中心到直线 l的距离为 .(结果保留根号)
12.若同一个圆的内接正三角形、正方形、正六边形的边心距分别为求的值.
13.如图所示,已知等边△ABC内接于⊙O,BD为⊙O内接正十二边形的一边,CD=5 cm,求⊙O的半径R.
快乐拓展
14.在一节数学实践活动课上,老师拿出三个边长都为5cm 的正方形硬纸板,他向同学们提出了这样一个问题:若将三个正方形纸板不重叠地放在桌面上,用一个圆形硬纸板将其盖住,这样的圆形硬纸板的最小直径应有多大 问题提出后,同学们经过讨论,大家觉得本题实际上就是求将三个正方形硬纸板无重叠地适当放置,圆形硬纸板能盖住时的最小直径.老师将同学们讨论过程中探索出的三种不同摆放类型的图形画在黑板上,如图所示:
(1)通过计算(结果保留根号与π).
①图1能盖住三个正方形所需的圆形硬纸板最小直径应为 cm;
②图2 能盖住三个正方形所需的圆形硬纸板最小直径为 cm;
③图3能盖住三个正方形所需的圆形硬纸板最小直径为 cm;
(2)其实上面三种放置方法所需的圆形硬纸板的直径都不是最小的,请你画出用圆形硬纸板盖住三个正方形时直径最小的放置方法(只要画出示意图,不要求说明理由),并求出此时圆形硬纸板的直径.
参考答案
1. B 2. D 3. A 4. A 5. C 6. D 7. B
8. B 解析:如图,连接OA,OD,OF,OH,
∵六边形ABCDEF是⊙O的内接正六边形,
OC=OD.
∴△AOF,△COD是正三角形.∴∠OAF=∠OFA=60°.
∵四边形 AFHG是正方形,∴AF=HF=AG,∠AFH=∠FAG=90°.
∴∠FOH=∠FHO=∠AGO=∠AOG=
由对称性可知, 45°.
9. 10.108° 11.(1)30 (2)2
12.解:设圆的半径为R,
则
13.解:如图所示,连接OB,OC,OD.
∵等边△ABC内接于⊙O,BD 为内接正十二边形的一边,
∴∠COD=∠BOC-∠BOD=90°.
∵OC=OD,∴∠OCD=45°,
即⊙O的半径R 为 5cm .
14.解:(1)①如图1,连接 BD,
∵AD=3×5=15(cm),AB=5cm,
故答案为:
②如图2,
∵三个正方形的边长均为5cm ,
∴A,B,C三点在以O为圆心,以OA为半径的圆上.
∴能盖住三个正方形所需的圆形硬纸板最小直径为10 cm;
故答案为:10
③如图3,
∴AD是过A,B,D三点的圆的直径.
∵OA=OB=OD,∴O为圆心.
∴⊙O的半径为OA,
∴能盖住三个正方形所需的圆形硬纸板最小直径为
故答案为:10
(2)如图4为盖住三个正方形时直径最小的放置方法,
连接OB,ON,延长OH 交 AB 于点 P,则OP⊥AB,P为AB中点,设OG=x,则OP=10-x,
则有 解得
则 ∴直径为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 圆
8 正多边形和圆
轻松过关
1.下列命题:①各角相等的多边形是正多边形 ②任何正多边形都有一个外接圆和一个内切圆,并且这两个圆是同心圆 ③正六边形的外接圆半径与边长相等 ④在正多边形中,中心角与正多边形的每个外角相等.其中,真命题的个数是
( )
A.4个 B.3个 C.2个 D.1个
2.如图,正三角形和正六边形都内接于⊙O,连接OC,则 ( )
A.90° B.100° C.110° D.120°
3.如图,点P ~P 是⊙O 的八等分点.若△P P P ,四边形 P P P P 的周长分别为a,b,则下列正确的是 ( )
大小无法比较
4.如图,⊙O与正五边形ABCDE的两边AE,CD相切于A,C两点,则∠AOC的度数是 ( )
A.144° B.130° C.129° D.108°
5.已知,正六边形 ABCDEF 的面积为 6,则正六边形的边长为 ( )
A.1 B. C.2 D.4
6.一个适当大的正六边形,它的一个顶点与一个边长为定值的小正六边形ABCDEF 的中心O 重合,且与边 AB,CD相交于G,H(如图).图中阴影部分的面积记为 S,三条线段 GB,BC,CH 的长度之和记为l,在大正六边形绕点O旋转过程中,下列说法正确的是( )
A. S变化, 不变 B. S不变,变化
C. S变化, 变化 D. S与 均不变
7.我们知道,五边形具有不稳定性,正五边形OABCD 在平面直角坐标系中的位置如图1所示,A在x 轴负半轴上,固定边 AO,将正五边形向右推,使点A,B,C共线,且点C落在y轴上,如图2所示,此时∠CDO的度数为 ( )
A.108° B.120° C.135° D.150°
8.如图,点O为正六边形ABCDEF的外接圆圆心,四边形AGHF为正方形,则的度数为 ( )
A.50° B.45° C.35° D.30°
9.如图,AE,DF是正八边形 ABCDEFGH 的两条对角线,则 .
第9题图 第10题图
10.如图,正五边形ABCDE中,点F是边CD的中点,AF,BC的延长线交于点N,点P是AN上一个动点,点M是BN上一个动点,当PB+PM的值最小时,∠BPN= .
11.将三个相同的六角形螺母并排摆放在桌面上,其俯视图如图1,正六边形边长为2 且各有一个顶点在直线l上.两侧螺母不动,把中间螺母抽出并重新摆放后,其俯视图如图2,其中,中间正六边形的一边与直线 l平行,有两边分别经过两侧正六边形的一个顶点.则图2中:
(1)∠α= 度;
(2)中间正六边形的中心到直线 l的距离为 .(结果保留根号)
12.若同一个圆的内接正三角形、正方形、正六边形的边心距分别为求的值.
13.如图所示,已知等边△ABC内接于⊙O,BD为⊙O内接正十二边形的一边,CD=5 cm,求⊙O的半径R.
快乐拓展
14.在一节数学实践活动课上,老师拿出三个边长都为5cm 的正方形硬纸板,他向同学们提出了这样一个问题:若将三个正方形纸板不重叠地放在桌面上,用一个圆形硬纸板将其盖住,这样的圆形硬纸板的最小直径应有多大 问题提出后,同学们经过讨论,大家觉得本题实际上就是求将三个正方形硬纸板无重叠地适当放置,圆形硬纸板能盖住时的最小直径.老师将同学们讨论过程中探索出的三种不同摆放类型的图形画在黑板上,如图所示:
(1)通过计算(结果保留根号与π).
①图1能盖住三个正方形所需的圆形硬纸板最小直径应为 cm;
②图2 能盖住三个正方形所需的圆形硬纸板最小直径为 cm;
③图3能盖住三个正方形所需的圆形硬纸板最小直径为 cm;
(2)其实上面三种放置方法所需的圆形硬纸板的直径都不是最小的,请你画出用圆形硬纸板盖住三个正方形时直径最小的放置方法(只要画出示意图,不要求说明理由),并求出此时圆形硬纸板的直径.
参考答案
1. B 2. D 3. A 4. A 5. C 6. D 7. B
8. B 解析:如图,连接OA,OD,OF,OH,
∵六边形ABCDEF是⊙O的内接正六边形,
OC=OD.
∴△AOF,△COD是正三角形.∴∠OAF=∠OFA=60°.
∵四边形 AFHG是正方形,∴AF=HF=AG,∠AFH=∠FAG=90°.
∴∠FOH=∠FHO=∠AGO=∠AOG=
由对称性可知, 45°.
9. 10.108° 11.(1)30 (2)2
12.解:设圆的半径为R,
则
13.解:如图所示,连接OB,OC,OD.
∵等边△ABC内接于⊙O,BD 为内接正十二边形的一边,
∴∠COD=∠BOC-∠BOD=90°.
∵OC=OD,∴∠OCD=45°,
即⊙O的半径R 为 5cm .
14.解:(1)①如图1,连接 BD,
∵AD=3×5=15(cm),AB=5cm,
故答案为:
②如图2,
∵三个正方形的边长均为5cm ,
∴A,B,C三点在以O为圆心,以OA为半径的圆上.
∴能盖住三个正方形所需的圆形硬纸板最小直径为10 cm;
故答案为:10
③如图3,
∴AD是过A,B,D三点的圆的直径.
∵OA=OB=OD,∴O为圆心.
∴⊙O的半径为OA,
∴能盖住三个正方形所需的圆形硬纸板最小直径为
故答案为:10
(2)如图4为盖住三个正方形时直径最小的放置方法,
连接OB,ON,延长OH 交 AB 于点 P,则OP⊥AB,P为AB中点,设OG=x,则OP=10-x,
则有 解得
则 ∴直径为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
