第五章 圆 阶段性检测(第7、8节)(含答案)
文档属性
| 名称 | 第五章 圆 阶段性检测(第7、8节)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 414.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-01 13:32:16 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第五章 圆
阶段性检测(第7、8节)
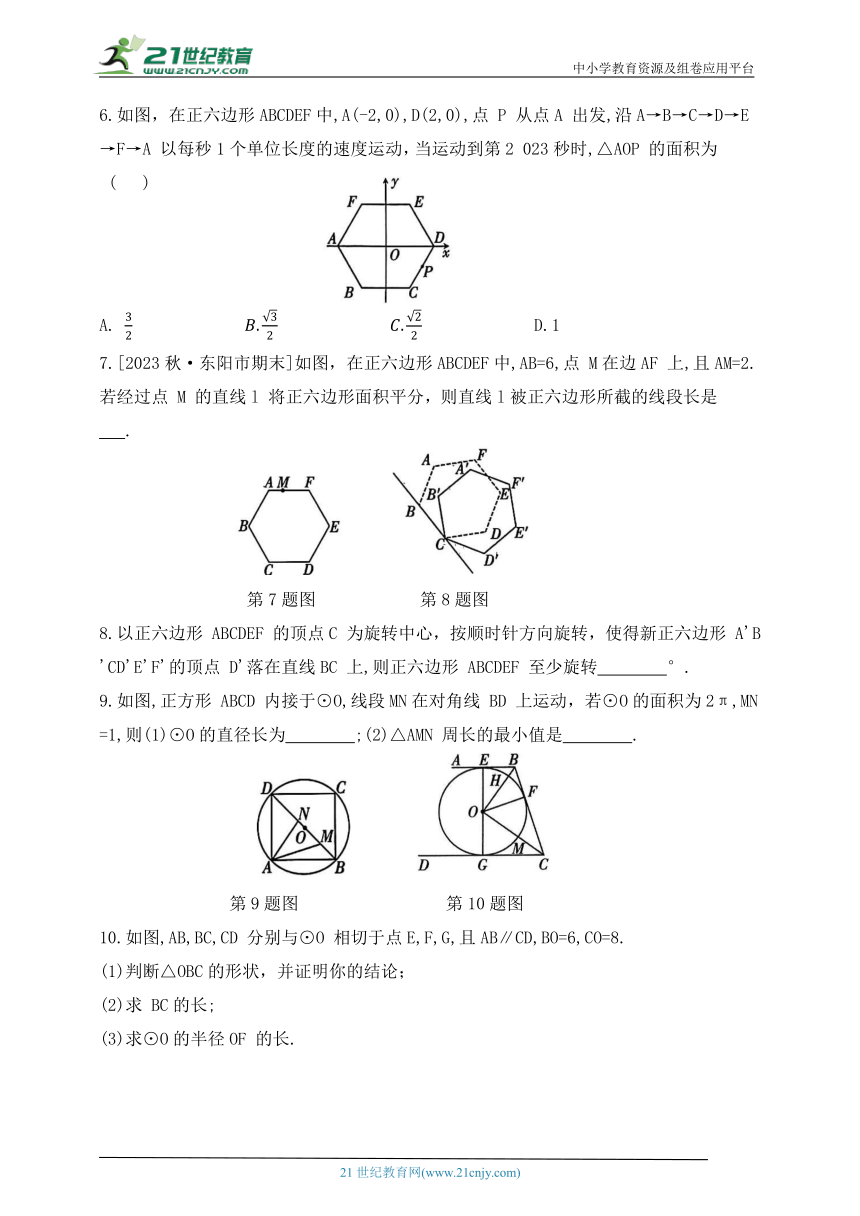
1.如图,AB,AC,BD是⊙O的切线,切点分别是 P,C,D.若 AB=5,AC=3,则 BD 的长是 ( )
A.4 B.3 C.2 D.1
第1题图 第2题图
2.如图,在矩形 ABCD中,AB=3,BC=2,以BC为直径在矩形内作半圆,自点 A 作半圆的切线AE,则sin∠CBE= ( )
B. C.
3.如图所示,已知 PA,PB 是⊙O的两条切线,A,B 为切点,线段 OP 交⊙O于点M.给出下列四种说法:
①PA= PB ②OP⊥AB ③四边形OAPB有外接圆 ④M是△AOP 外接圆的圆心.其中正确说法的个数是 ( )
A.1个 B.2个 C.3个 D.4个
第3题图 第4题图
4.如图,正六边形ABCDEF的顶点A,F分别在正方形BMGH的边BH,GH 上.若正方形的边长为6,则正六边形的边长为 ( )
A.2 B.4 C.4.5 D.5
5.第29届自贡国际恐龙灯会“辉煌新时代”主题灯组上有一幅不完整的正多边形图案,小华量得图中一边与对角线的夹角∠ACB=15°,算出这个正多边形的
边数是( )
A. 9 B. 10 C. 11 D. 12
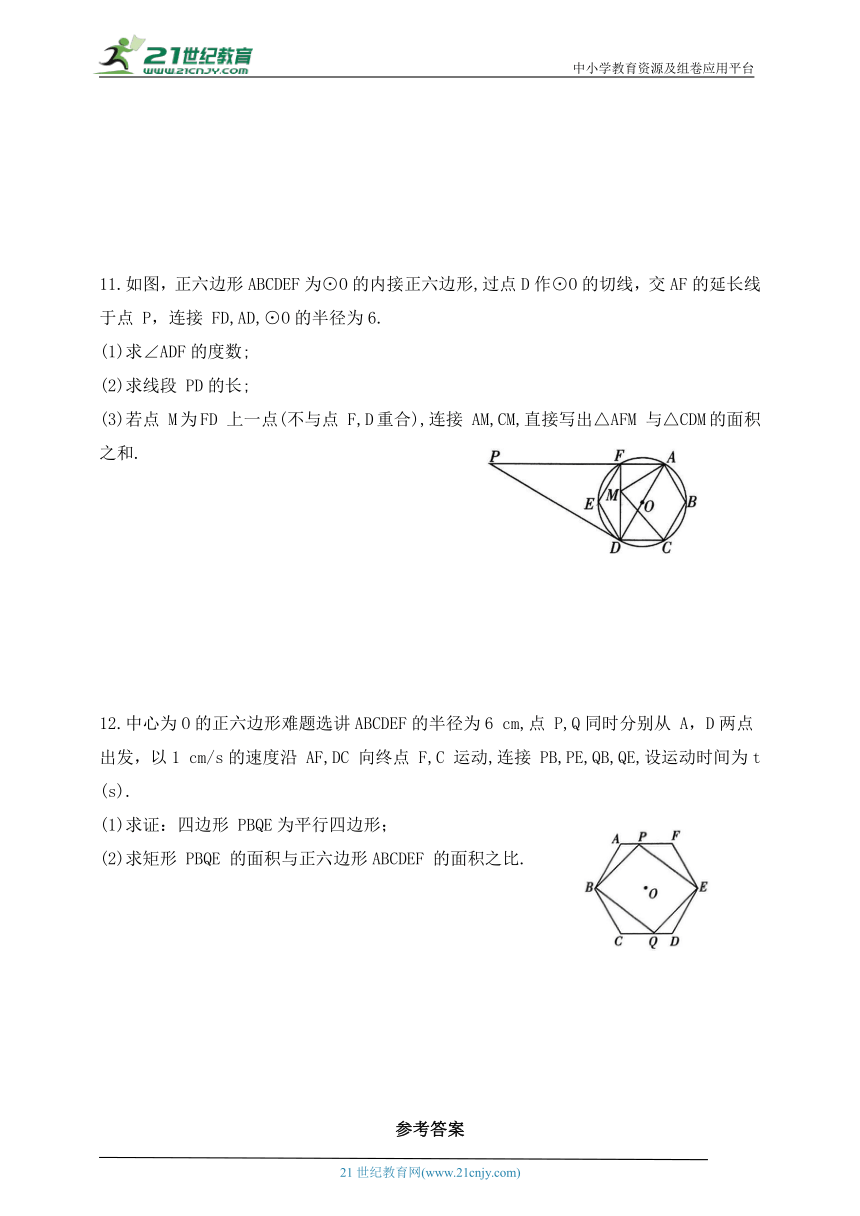
6.如图,在正六边形ABCDEF中,A(-2,0),D(2,0),点 P 从点A 出发,沿A→B→C→D→E→F→A 以每秒1个单位长度的速度运动,当运动到第2 023秒时,△AOP 的面积为 ( )
A. D.1
7.[2023秋·东阳市期末]如图,在正六边形ABCDEF中,AB=6,点 M在边AF 上,且AM=2.若经过点 M 的直线l 将正六边形面积平分,则直线l被正六边形所截的线段长是 .
第7题图 第8题图
8.以正六边形 ABCDEF 的顶点C 为旋转中心,按顺时针方向旋转,使得新正六边形 A'B'CD'E'F'的顶点 D'落在直线BC 上,则正六边形 ABCDEF 至少旋转 °.
9.如图,正方形 ABCD 内接于⊙O,线段MN在对角线 BD 上运动,若⊙O的面积为2π,MN=1,则(1)⊙O的直径长为 ;(2)△AMN 周长的最小值是 .
第9题图 第10题图
10.如图,AB,BC,CD 分别与⊙O 相切于点E,F,G,且AB∥CD,BO=6,CO=8.
(1)判断△OBC的形状,并证明你的结论;
(2)求 BC的长;
(3)求⊙O的半径OF 的长.
11.如图,正六边形ABCDEF为⊙O的内接正六边形,过点D作⊙O的切线,交AF的延长线于点 P,连接 FD,AD,⊙O的半径为6.
(1)求∠ADF的度数;
(2)求线段 PD的长;
(3)若点 M为FD 上一点(不与点 F,D重合),连接 AM,CM,直接写出△AFM 与△CDM的面积之和.
12.中心为O的正六边形难题选讲ABCDEF的半径为6 cm,点 P,Q同时分别从 A,D两点出发,以1 cm/s的速度沿 AF,DC 向终点 F,C 运动,连接 PB,PE,QB,QE,设运动时间为t(s).
(1)求证:四边形 PBQE为平行四边形;
(2)求矩形 PBQE 的面积与正六边形ABCDEF 的面积之比.
参考答案
1. C 2. D 3. C 4. B 5. D 6. B 7.4 8. 60
9.(1)2 (2)4
解析:(1)∵⊙O的面积为2π,∴圆的半径为
(2)由正方形的性质,知点C是点A 关于BD的对称点,
过点C作CA'∥BD,且使CA'=1,
连接 AA'交 BD 于点 N,取 NM=1,连接AM,CM,则点 M,N为所求点,
∵A'C∥MN,且A'C=MN,∴四边形 MCA'N 为平行四边形.
∴A'N=CM=AM.
故△AMN的周长=AM+AN+MN=AA'+1为最小,
∴△AMN 的周长的最小值为3+1=4.
10.解:(1)△OBC是直角三角形.
证明:∵AB,BC分别与⊙O相切于点E,F,∴∠OEB=∠OFB=90°,EB=FB,
又∵OB=OB,∴Rt△OEB≌Rt△OFB(HL),
同理得
∵AB∥CD,∴∠EBF+∠GCF=180°.∴∠OBF+∠OCF=90°.
∴△OBC是直角三角形;
(2)∵在 Rt△BOC中,BO=6,CO=8,
(3)∵AB,BC,CD分别与⊙O相切于点 E,F,G,∴OF⊥BC.
11.解:(1)如图,连接FO,
∵正六边形 ABCDEF为⊙O的内接正六边形,
∴AD为⊙O的直径,∠AFD=90°,∠AOF=60°.
(2)∵PD与⊙O相切,AD为⊙O的直径,
∵正六边形ABCDEF为⊙O的内接正六边形,∴∠PAD=60°,
在 Rt△PAD中,AD=12,
S△AFD,
在 Rt△AFD中,AF=AD·cos∠FAD=12×cos60°=6,
DF=AD·sin∠FAD=12×sin60°=6
12.解:(1)证明:连接AO,∵六边形 ABCDEF是正六边形,半径为6 cm,
∴AB=BC=CD=DE=EF=FA=AO=6cm,∠BAF =∠ABC =∠BCD =∠CDE =∠DEF=∠EFA,
∵点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC 向终点F,C运动,
∴AP=DQ=t cm,PF=QC=(6-t) cm,
在△ABP和△DEQ中,
∴△ABP≌△DEQ(SAS),∴BP=EQ.
同理可证 PE=QB,∴四边形 PEQB 为平行四边形;
(2)连接BE,AE,BD,BF,CE,则 BE=2OA=12 cm.
①当t=0时,点 P 与A 重合,Q与 D 重合,四边形PBQE 即为四边形ABDE,如
图所示:
则∠EAF=∠AEF=30°.
∴此时平行四边形 PBQE 是矩形;
②当t=6时,点 P与F重合,Q与C重合,四边形 PBQE 即为四边形 FBCE,如图所示:同理可知∠BFE=90°,此时平行四边形PBQE是矩形.
综上所述,t=0s或6s时,四边形PBQE是矩形,
∴矩形 PBQE 的面积=矩形 ABDE 的面积
∵正六边形 ABCDEF 的面积
∴矩形 PBQE 的面积:正六边形ABCDEF的面积
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 圆
阶段性检测(第7、8节)
1.如图,AB,AC,BD是⊙O的切线,切点分别是 P,C,D.若 AB=5,AC=3,则 BD 的长是 ( )
A.4 B.3 C.2 D.1
第1题图 第2题图
2.如图,在矩形 ABCD中,AB=3,BC=2,以BC为直径在矩形内作半圆,自点 A 作半圆的切线AE,则sin∠CBE= ( )
B. C.
3.如图所示,已知 PA,PB 是⊙O的两条切线,A,B 为切点,线段 OP 交⊙O于点M.给出下列四种说法:
①PA= PB ②OP⊥AB ③四边形OAPB有外接圆 ④M是△AOP 外接圆的圆心.其中正确说法的个数是 ( )
A.1个 B.2个 C.3个 D.4个
第3题图 第4题图
4.如图,正六边形ABCDEF的顶点A,F分别在正方形BMGH的边BH,GH 上.若正方形的边长为6,则正六边形的边长为 ( )
A.2 B.4 C.4.5 D.5
5.第29届自贡国际恐龙灯会“辉煌新时代”主题灯组上有一幅不完整的正多边形图案,小华量得图中一边与对角线的夹角∠ACB=15°,算出这个正多边形的
边数是( )
A. 9 B. 10 C. 11 D. 12
6.如图,在正六边形ABCDEF中,A(-2,0),D(2,0),点 P 从点A 出发,沿A→B→C→D→E→F→A 以每秒1个单位长度的速度运动,当运动到第2 023秒时,△AOP 的面积为 ( )
A. D.1
7.[2023秋·东阳市期末]如图,在正六边形ABCDEF中,AB=6,点 M在边AF 上,且AM=2.若经过点 M 的直线l 将正六边形面积平分,则直线l被正六边形所截的线段长是 .
第7题图 第8题图
8.以正六边形 ABCDEF 的顶点C 为旋转中心,按顺时针方向旋转,使得新正六边形 A'B'CD'E'F'的顶点 D'落在直线BC 上,则正六边形 ABCDEF 至少旋转 °.
9.如图,正方形 ABCD 内接于⊙O,线段MN在对角线 BD 上运动,若⊙O的面积为2π,MN=1,则(1)⊙O的直径长为 ;(2)△AMN 周长的最小值是 .
第9题图 第10题图
10.如图,AB,BC,CD 分别与⊙O 相切于点E,F,G,且AB∥CD,BO=6,CO=8.
(1)判断△OBC的形状,并证明你的结论;
(2)求 BC的长;
(3)求⊙O的半径OF 的长.
11.如图,正六边形ABCDEF为⊙O的内接正六边形,过点D作⊙O的切线,交AF的延长线于点 P,连接 FD,AD,⊙O的半径为6.
(1)求∠ADF的度数;
(2)求线段 PD的长;
(3)若点 M为FD 上一点(不与点 F,D重合),连接 AM,CM,直接写出△AFM 与△CDM的面积之和.
12.中心为O的正六边形难题选讲ABCDEF的半径为6 cm,点 P,Q同时分别从 A,D两点出发,以1 cm/s的速度沿 AF,DC 向终点 F,C 运动,连接 PB,PE,QB,QE,设运动时间为t(s).
(1)求证:四边形 PBQE为平行四边形;
(2)求矩形 PBQE 的面积与正六边形ABCDEF 的面积之比.
参考答案
1. C 2. D 3. C 4. B 5. D 6. B 7.4 8. 60
9.(1)2 (2)4
解析:(1)∵⊙O的面积为2π,∴圆的半径为
(2)由正方形的性质,知点C是点A 关于BD的对称点,
过点C作CA'∥BD,且使CA'=1,
连接 AA'交 BD 于点 N,取 NM=1,连接AM,CM,则点 M,N为所求点,
∵A'C∥MN,且A'C=MN,∴四边形 MCA'N 为平行四边形.
∴A'N=CM=AM.
故△AMN的周长=AM+AN+MN=AA'+1为最小,
∴△AMN 的周长的最小值为3+1=4.
10.解:(1)△OBC是直角三角形.
证明:∵AB,BC分别与⊙O相切于点E,F,∴∠OEB=∠OFB=90°,EB=FB,
又∵OB=OB,∴Rt△OEB≌Rt△OFB(HL),
同理得
∵AB∥CD,∴∠EBF+∠GCF=180°.∴∠OBF+∠OCF=90°.
∴△OBC是直角三角形;
(2)∵在 Rt△BOC中,BO=6,CO=8,
(3)∵AB,BC,CD分别与⊙O相切于点 E,F,G,∴OF⊥BC.
11.解:(1)如图,连接FO,
∵正六边形 ABCDEF为⊙O的内接正六边形,
∴AD为⊙O的直径,∠AFD=90°,∠AOF=60°.
(2)∵PD与⊙O相切,AD为⊙O的直径,
∵正六边形ABCDEF为⊙O的内接正六边形,∴∠PAD=60°,
在 Rt△PAD中,AD=12,
S△AFD,
在 Rt△AFD中,AF=AD·cos∠FAD=12×cos60°=6,
DF=AD·sin∠FAD=12×sin60°=6
12.解:(1)证明:连接AO,∵六边形 ABCDEF是正六边形,半径为6 cm,
∴AB=BC=CD=DE=EF=FA=AO=6cm,∠BAF =∠ABC =∠BCD =∠CDE =∠DEF=∠EFA,
∵点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC 向终点F,C运动,
∴AP=DQ=t cm,PF=QC=(6-t) cm,
在△ABP和△DEQ中,
∴△ABP≌△DEQ(SAS),∴BP=EQ.
同理可证 PE=QB,∴四边形 PEQB 为平行四边形;
(2)连接BE,AE,BD,BF,CE,则 BE=2OA=12 cm.
①当t=0时,点 P 与A 重合,Q与 D 重合,四边形PBQE 即为四边形ABDE,如
图所示:
则∠EAF=∠AEF=30°.
∴此时平行四边形 PBQE 是矩形;
②当t=6时,点 P与F重合,Q与C重合,四边形 PBQE 即为四边形 FBCE,如图所示:同理可知∠BFE=90°,此时平行四边形PBQE是矩形.
综上所述,t=0s或6s时,四边形PBQE是矩形,
∴矩形 PBQE 的面积=矩形 ABDE 的面积
∵正六边形 ABCDEF 的面积
∴矩形 PBQE 的面积:正六边形ABCDEF的面积
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
