第五章 圆 专项训练 圆中常用的辅助线(含答案)
文档属性
| 名称 | 第五章 圆 专项训练 圆中常用的辅助线(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 512.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-01 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第五章 圆
专项训练 圆中常用的辅助线
类型一 连半径,构造等腰三角形
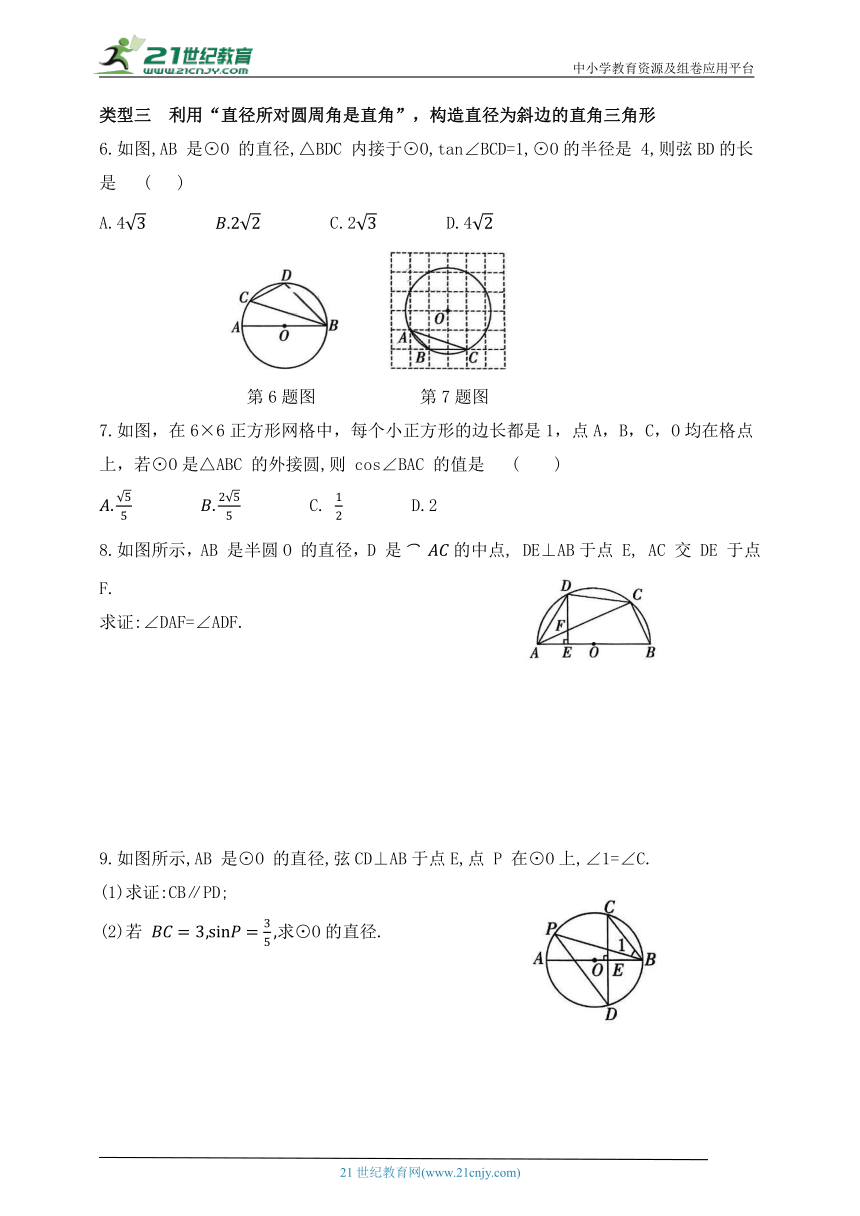
1.已知⊙O中半径OC=3,∠BAC=45°,则弦BC的长度为 ( )
A.3 B. C. D.
第1题图 第2题图
2.如图,圆O的半径是4,BC是弦,∠B=30°且A是BC的中点,则弦AB的长为( )
C.4 D.6
3.如图,在⊙O中,∠A=30°,劣弧的度数是 ( )
A.30° B.60° C.90° D.120°
类型二 作与弦垂直的半径(或弦心距)构造直角三角形
4.如图,把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,若EF=CD=4,则截面⊙O的半径等于 ( )
A. B. C. D.
第4题图 第5题图
5.如图,⊙O 的弦AB 垂直于CD,点 E 为垂足,连接OE.若 AE=1,AB=CD=6,则OE的值是 ( )
A.2 B.3 C.4
类型三 利用“直径所对圆周角是直角”,构造直径为斜边的直角三角形
6.如图,AB 是⊙O 的直径,△BDC 内接于⊙O,tan∠BCD=1,⊙O的半径是 4,则弦BD的长是 ( )
A.4 C.2 D.4
第6题图 第7题图
7.如图,在6×6正方形网格中,每个小正方形的边长都是1,点A,B,C,O均在格点上,若⊙O是△ABC 的外接圆,则 cos∠BAC 的值是 ( )
C. D.2
8.如图所示,AB 是半圆O 的直径,D 是 的中点, DE⊥AB于点 E, AC 交 DE 于点F.
求证:∠DAF=∠ADF.
9.如图所示,AB 是⊙O 的直径,弦CD⊥AB于点E,点 P 在⊙O上,∠1=∠C.
(1)求证:CB∥PD;
(2)若 求⊙O的直径.
10.已知△ABC,以 AB 为直径的⊙O分别交AC 于点 D,交 BC 于点 E,连接 ED,若ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=2求CD的长.
类型四 构造同弧或等弧所对的圆周角
11.如图,AB是⊙O的弦,C为⊙O上一点,过点 C作AB 的垂线与AB 的延长线交于点D,连接 BO并延长,与⊙O交于点E,连接EC,∠ABE=2∠E.
(1)求证:CD是⊙O的切线;
(2)若 求AB的长.
12.在学习《圆》这一单元时,我们学习了圆周角定理及其推论:同弧或(等弧)所对的圆周角相等,直径所对的圆周角是直角.
【观察发现】如图1,AB 为⊙O的直径,点C在弦AB 所对的弧上,根据圆周角定理,我们知道∠ACB 的度数 (填“变”或“不变”);因此,我们可以得到当∠ACB=∠ADB时,点 C,D在以 AB为弦的同弧上;
【探索应用】如图 2,在△ABC 中,∠A=60°,BC=4,求△ABC面积的最大值.
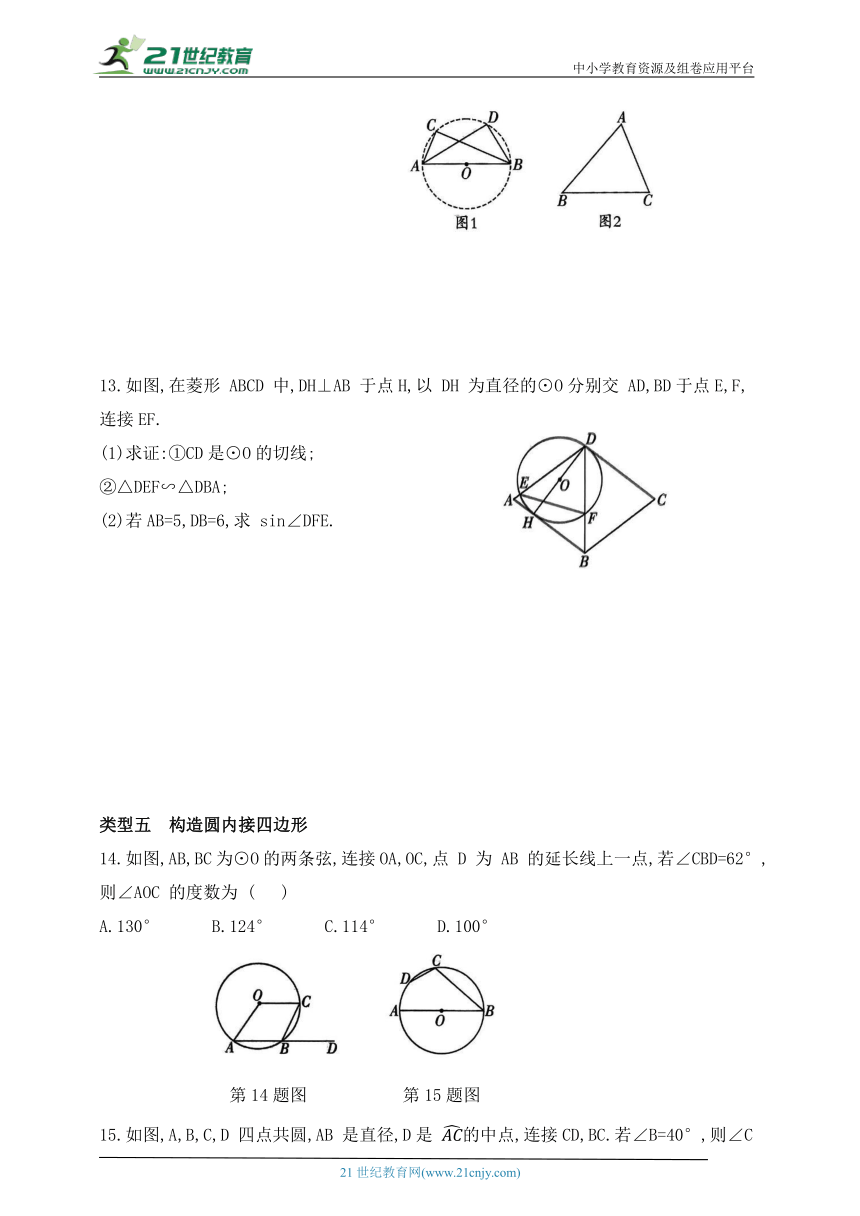
13.如图,在菱形 ABCD 中,DH⊥AB 于点H,以 DH 为直径的⊙O分别交 AD,BD于点E,F,连接EF.
(1)求证:①CD是⊙O的切线;
②△DEF∽△DBA;
(2)若AB=5,DB=6,求 sin∠DFE.
类型五 构造圆内接四边形
14.如图,AB,BC为⊙O的两条弦,连接OA,OC,点 D 为 AB 的延长线上一点,若∠CBD=62°,则∠AOC 的度数为 ( )
A.130° B.124° C.114° D.100°
第14题图 第15题图
15.如图,A,B,C,D 四点共圆,AB 是直径,D是 的中点,连接CD,BC.若∠B=40°,则∠C的大小为 ( )
A.90° B.100° C.110° D.120°
类型六 与切线有关的问题添加过切点的半径(或直径)
16.如图,四边形 ABCD的两边AD,CD与⊙O相切于A,C 两点,点 B 在⊙O 上,若∠D=50°,则∠B 的度数为 ( )
A.130° B.65° C.60° D.50°
17.如图,AB 是⊙O 的切线,B 为切点,连接 AO交⊙O于点C,延长 AO交⊙O 于点 D,连接 BD.若∠A=∠D,且AC=3,则AB的长度是 ( )
A.3 B.4 C.3
第17题图 第18题图
18.如图,在⊙O中,AB切⊙O于点 A,连接OB 交⊙O于点 C,过点 A作 AD∥OB 交⊙O 于点 D,连接 CD. 若∠ABO=40°,则∠OCD为 ( )
A.15° B.20° C.25° D.30°
19.如 图, 在 Rt△ABC中,∠C=90°,E为AB 边上一点,以 AE 为直径的半圆O 与BC 相切于点 D,连接 AD,BE=3,BD=3 P 是AB 边上的动点,当△ADP 为等腰三角形时,AP 的长为 .
参考答案
1. C 2. C 3. D 4. C 5. A 6. D 7. B
8.证明:连接BD.
∵D为AC的中点,∴∠ABD=∠DAC,
∵AB为半圆O的直径,DE⊥AB,∴∠DEA=∠ADB=90°,
∴∠ADF+∠DAE=∠DAE+∠ABD=90°,∴∠ADF=∠ABD,
∴∠DAF=∠ADF.
9.解:(1)证明:∵∠C=∠P,∠1=∠C,∴∠1=∠P.∴CB∥PD;
(2)如图所示,连接AC.
∵AB为⊙O的直径,∴∠ACB=90°.
又∵CD⊥AB,∴BC=BD.∴∠A=∠P.
即
又∵BC=3,∴AB=5.∴⊙O的直径为5.
10.解:(1)证明:∵ED=EC,∴∠EDC=∠C.
∵∠EDC=∠B,∴∠B=∠C.∴AB=AC;
(2)方法一:
如图1所示,连接AE.
∵AB为⊙O的直径,∴AE⊥BC.
由(1)知AB=AC=4,
∵∠EDC=∠B,∠C=∠C,∴△CDE∽△CBA.
方法二:
如图2所示,连接BD.
∵AB为⊙O的直径,∴BD⊥AC.
设CD=a,由(1)知AC=AB=4,则AD=4-a,
在 Rt△BCD中,由勾股定理,得
在 Rt△ABD中,由勾股定理,得.
∴解得 即
11.解:(1)证明:连接OC,则∠BOC=2∠E.
∵∠ABE=2∠E,∴∠ABE=∠BOC.∴AB∥OC.
∵AB⊥CD,∴OC⊥CD.
∵OC是⊙O的半径,∴CD是⊙O的切线;
(2)连接AC,BC,
∵BE 是⊙O的直径,∴∠BCE=90°.∴∠OCE+∠OCB=90°.
∵∠OCB+∠BCD=90°,∴∠BCD=∠OCE.∴∠BCD=∠E.
∴CD=3,AD=9.∴AB=8.
12.解:【观察发现】根据圆周角定理,我们知道∠ACB的度数不变,故答案为:不变;
【探索应用】如图,作出△ABC 的外接圆⊙O,连接OB,OC,当△ABC的 BC 边上的高经过点 O 时,点A 与 BC 距离最大,△ABC面积最大,
∵OB=OC,∴点O在BC 的垂直平分线上,∠OBC=∠OCB.
∵∠BOC=2∠BAC=120°,∴∠OBC=∠OCB=30°.
又∵OE垂直平分BC, OE.
∴△ABC的最大的面积为 4
13.解:(1)证明:①∵四边形 ABCD是菱形,∴AB∥CD.
∵DH⊥AB,∴∠CDH=∠DHA=90°.∴CD⊥OD.
∵OD为⊙O的半径,∴CD 是⊙O的切线;
②连接HF,∴∠DEF=∠DHF.
∵DH为⊙O直径,∴∠DFH=90°.
∵∠DHB=90°, ∴∠DHF=∠DBA=∠DEF.
∵∠EDF=∠BDA,∴△DEF∽△DBA;
(2)连接AC交BD 于点G.
∵四边形 ABCD为菱形,BD=6,∴AC⊥BD,AG=GC,DG=GB=3.
在Rt△AGB中, ∴AC=2AG=8.
∵△DEF∽△DBA,∴∠DFE=∠DAH,
14. B 15. C 16. B 17. C 18. C
或6
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 圆
专项训练 圆中常用的辅助线
类型一 连半径,构造等腰三角形
1.已知⊙O中半径OC=3,∠BAC=45°,则弦BC的长度为 ( )
A.3 B. C. D.
第1题图 第2题图
2.如图,圆O的半径是4,BC是弦,∠B=30°且A是BC的中点,则弦AB的长为( )
C.4 D.6
3.如图,在⊙O中,∠A=30°,劣弧的度数是 ( )
A.30° B.60° C.90° D.120°
类型二 作与弦垂直的半径(或弦心距)构造直角三角形
4.如图,把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,若EF=CD=4,则截面⊙O的半径等于 ( )
A. B. C. D.
第4题图 第5题图
5.如图,⊙O 的弦AB 垂直于CD,点 E 为垂足,连接OE.若 AE=1,AB=CD=6,则OE的值是 ( )
A.2 B.3 C.4
类型三 利用“直径所对圆周角是直角”,构造直径为斜边的直角三角形
6.如图,AB 是⊙O 的直径,△BDC 内接于⊙O,tan∠BCD=1,⊙O的半径是 4,则弦BD的长是 ( )
A.4 C.2 D.4
第6题图 第7题图
7.如图,在6×6正方形网格中,每个小正方形的边长都是1,点A,B,C,O均在格点上,若⊙O是△ABC 的外接圆,则 cos∠BAC 的值是 ( )
C. D.2
8.如图所示,AB 是半圆O 的直径,D 是 的中点, DE⊥AB于点 E, AC 交 DE 于点F.
求证:∠DAF=∠ADF.
9.如图所示,AB 是⊙O 的直径,弦CD⊥AB于点E,点 P 在⊙O上,∠1=∠C.
(1)求证:CB∥PD;
(2)若 求⊙O的直径.
10.已知△ABC,以 AB 为直径的⊙O分别交AC 于点 D,交 BC 于点 E,连接 ED,若ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=2求CD的长.
类型四 构造同弧或等弧所对的圆周角
11.如图,AB是⊙O的弦,C为⊙O上一点,过点 C作AB 的垂线与AB 的延长线交于点D,连接 BO并延长,与⊙O交于点E,连接EC,∠ABE=2∠E.
(1)求证:CD是⊙O的切线;
(2)若 求AB的长.
12.在学习《圆》这一单元时,我们学习了圆周角定理及其推论:同弧或(等弧)所对的圆周角相等,直径所对的圆周角是直角.
【观察发现】如图1,AB 为⊙O的直径,点C在弦AB 所对的弧上,根据圆周角定理,我们知道∠ACB 的度数 (填“变”或“不变”);因此,我们可以得到当∠ACB=∠ADB时,点 C,D在以 AB为弦的同弧上;
【探索应用】如图 2,在△ABC 中,∠A=60°,BC=4,求△ABC面积的最大值.
13.如图,在菱形 ABCD 中,DH⊥AB 于点H,以 DH 为直径的⊙O分别交 AD,BD于点E,F,连接EF.
(1)求证:①CD是⊙O的切线;
②△DEF∽△DBA;
(2)若AB=5,DB=6,求 sin∠DFE.
类型五 构造圆内接四边形
14.如图,AB,BC为⊙O的两条弦,连接OA,OC,点 D 为 AB 的延长线上一点,若∠CBD=62°,则∠AOC 的度数为 ( )
A.130° B.124° C.114° D.100°
第14题图 第15题图
15.如图,A,B,C,D 四点共圆,AB 是直径,D是 的中点,连接CD,BC.若∠B=40°,则∠C的大小为 ( )
A.90° B.100° C.110° D.120°
类型六 与切线有关的问题添加过切点的半径(或直径)
16.如图,四边形 ABCD的两边AD,CD与⊙O相切于A,C 两点,点 B 在⊙O 上,若∠D=50°,则∠B 的度数为 ( )
A.130° B.65° C.60° D.50°
17.如图,AB 是⊙O 的切线,B 为切点,连接 AO交⊙O于点C,延长 AO交⊙O 于点 D,连接 BD.若∠A=∠D,且AC=3,则AB的长度是 ( )
A.3 B.4 C.3
第17题图 第18题图
18.如图,在⊙O中,AB切⊙O于点 A,连接OB 交⊙O于点 C,过点 A作 AD∥OB 交⊙O 于点 D,连接 CD. 若∠ABO=40°,则∠OCD为 ( )
A.15° B.20° C.25° D.30°
19.如 图, 在 Rt△ABC中,∠C=90°,E为AB 边上一点,以 AE 为直径的半圆O 与BC 相切于点 D,连接 AD,BE=3,BD=3 P 是AB 边上的动点,当△ADP 为等腰三角形时,AP 的长为 .
参考答案
1. C 2. C 3. D 4. C 5. A 6. D 7. B
8.证明:连接BD.
∵D为AC的中点,∴∠ABD=∠DAC,
∵AB为半圆O的直径,DE⊥AB,∴∠DEA=∠ADB=90°,
∴∠ADF+∠DAE=∠DAE+∠ABD=90°,∴∠ADF=∠ABD,
∴∠DAF=∠ADF.
9.解:(1)证明:∵∠C=∠P,∠1=∠C,∴∠1=∠P.∴CB∥PD;
(2)如图所示,连接AC.
∵AB为⊙O的直径,∴∠ACB=90°.
又∵CD⊥AB,∴BC=BD.∴∠A=∠P.
即
又∵BC=3,∴AB=5.∴⊙O的直径为5.
10.解:(1)证明:∵ED=EC,∴∠EDC=∠C.
∵∠EDC=∠B,∴∠B=∠C.∴AB=AC;
(2)方法一:
如图1所示,连接AE.
∵AB为⊙O的直径,∴AE⊥BC.
由(1)知AB=AC=4,
∵∠EDC=∠B,∠C=∠C,∴△CDE∽△CBA.
方法二:
如图2所示,连接BD.
∵AB为⊙O的直径,∴BD⊥AC.
设CD=a,由(1)知AC=AB=4,则AD=4-a,
在 Rt△BCD中,由勾股定理,得
在 Rt△ABD中,由勾股定理,得.
∴解得 即
11.解:(1)证明:连接OC,则∠BOC=2∠E.
∵∠ABE=2∠E,∴∠ABE=∠BOC.∴AB∥OC.
∵AB⊥CD,∴OC⊥CD.
∵OC是⊙O的半径,∴CD是⊙O的切线;
(2)连接AC,BC,
∵BE 是⊙O的直径,∴∠BCE=90°.∴∠OCE+∠OCB=90°.
∵∠OCB+∠BCD=90°,∴∠BCD=∠OCE.∴∠BCD=∠E.
∴CD=3,AD=9.∴AB=8.
12.解:【观察发现】根据圆周角定理,我们知道∠ACB的度数不变,故答案为:不变;
【探索应用】如图,作出△ABC 的外接圆⊙O,连接OB,OC,当△ABC的 BC 边上的高经过点 O 时,点A 与 BC 距离最大,△ABC面积最大,
∵OB=OC,∴点O在BC 的垂直平分线上,∠OBC=∠OCB.
∵∠BOC=2∠BAC=120°,∴∠OBC=∠OCB=30°.
又∵OE垂直平分BC, OE.
∴△ABC的最大的面积为 4
13.解:(1)证明:①∵四边形 ABCD是菱形,∴AB∥CD.
∵DH⊥AB,∴∠CDH=∠DHA=90°.∴CD⊥OD.
∵OD为⊙O的半径,∴CD 是⊙O的切线;
②连接HF,∴∠DEF=∠DHF.
∵DH为⊙O直径,∴∠DFH=90°.
∵∠DHB=90°, ∴∠DHF=∠DBA=∠DEF.
∵∠EDF=∠BDA,∴△DEF∽△DBA;
(2)连接AC交BD 于点G.
∵四边形 ABCD为菱形,BD=6,∴AC⊥BD,AG=GC,DG=GB=3.
在Rt△AGB中, ∴AC=2AG=8.
∵△DEF∽△DBA,∴∠DFE=∠DAH,
14. B 15. C 16. B 17. C 18. C
或6
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
