2025年九年级数学中考三轮冲刺练习四边形压轴题综合训练(含答案)
文档属性
| 名称 | 2025年九年级数学中考三轮冲刺练习四边形压轴题综合训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-01 15:07:20 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2025年九年级数学中考三轮冲刺练习四边形压轴题综合训练
一、选择题
1.如图,在 ABCD中,AC,BD相交于点O,AC=2,.过点A作AE⊥BC的垂线交BC于点E,记BE长为x,BC长为y.当x,y的值发生变化时,下列代数式的值不变的是( )
A.x+y B.x﹣y C.xy D.x2+y2
2.如图,在Rt△ABC中,∠C=90°,AC=12,BC=5,点P是边AB上任意一点,过点P作PD⊥AC,PE⊥BC,垂足分别为点D,E,连接DE,则DE的最小值是( )
A. B. C. D.
3.如图,矩形ABCD中,AB,BC=1,动点E,F分别从点A,C同时出发,以每秒1个单位长度的速度沿AB,CD向终点B,D运动,过点E,F作直线l,过点A作直线l的垂线,垂足为G,则AG的最大值为( )
A. B. C.2 D.1
4.如图,在边长为4的正方形ABCD中,点E是BC上一点,点F是CD延长线上一点,连接AE,AF,AM平分∠EAF交CD于点M.若BE=DF=1,则DM的长度为( )
A.2 B. C. D.
5.如图,在正方形ABCD中,点H在AD边上(不与点A、D重合),∠BHF=90°,HF交正方形外角的平分线DF于点F,连接AC交BH于点M,连接BF交AC于点G,交CD于点N,连接BD.则下列结论:
①∠HBF=45°;②点G是BF的中点;③若点H是AD的中点,则sin∠NBC;④BNBM;⑤若AHHD,则S△BNDS△AHM.其中正确的结论是( )
A.①②③④ B.①③⑤ C.①②④⑤ D.①②③④⑤
二、填空题
6.如图,在边长为10的菱形ABCD中,对角线AC,BD相交于点O,点E在BC延长线上,OE与CD相交于点F.若∠ACD=2∠OEC,,则菱形ABCD的面积为 .
7.如图,正方形ABCD的边长为1,M、N是边BC、CD上的动点.若∠MAN=45°,则MN的最小值为 .
8.如图,正方形ABCD的边长为,对角线AC,BD相交于点O,点E在CA的延长线上,OE=5,连接DE.
(Ⅰ)线段AE的长为 ;
(Ⅱ)若F为DE的中点,则线段AF的长为 .
9.如图,在边长为3的正方形ABCD的外侧,作等腰三角形ADE,EA=ED.
(1)△ADE的面积为 ;
(2)若F为BE的中点,连接AF并延长,与CD相交于点G,则AG的长为 .
10.出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建.“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一,如图,在矩形ABCD中,AB=5,AD=12,对角线AC与BD交于点O,点E为BC边上的一个动点,EF⊥AC,EG⊥BD,垂足分别为点F,G,则EF+EG= .
三、解答题
11.如图,在四边形ABCD中,E是AB的中点,DB,CE交于点F,DF=FB,AF∥DC.
(1)求证:四边形AFCD为平行四边形;
(2)若∠EFB=90°,tan∠FEB=3,EF=1,求BC的长.
12.如图,在菱形ABCD中,AB=10cm,∠ABC=60°,E为对角线AC上一动点,以DE为一边作∠DEF=60°,EF交射线BC于点F,连接BE,DF.点E从点C出发,沿CA方向以每秒2cm的速度运动至点A处停止.设△BEF的面积为y cm2,点E的运动时间为x秒.
(1)求证:BE=EF;
(2)求y与x的函数表达式,并写出自变量x的取值范围;
(3)求x为何值时,线段DF的长度最短.
13.如图,在菱形ABCD中,对角线AC,BD相交于点O,点P,Q分别是边BC,线段OD上的点,连接AP,QP,AP与OB相交于点E.
(1)如图1,连接QA.当QA=QP时,试判断点Q是否在线段PC的垂直平分线上,并说明理由;
(2)如图2,若∠APB=90°,且∠BAP=∠ADB,
①求证:AE=2EP;
②当OQ=OE时,设EP=a,求PQ的长(用含a的代数式表示).
14.如图,在正方形ABCD中,线段CD绕点C逆时针旋转到CE处,旋转角为α,点F在直线DE上,且AD=AF,连接BF.
(1)如图1,当0°<α<90°时,
①求∠BAF的大小(用含α的式子表示).
②求证:EFBF.
(2)如图2,取线段EF的中点G,连接AG,已知AB=2,请直接写出在线段CE旋转过程中(0°<α<360°)△ADG面积的最大值.
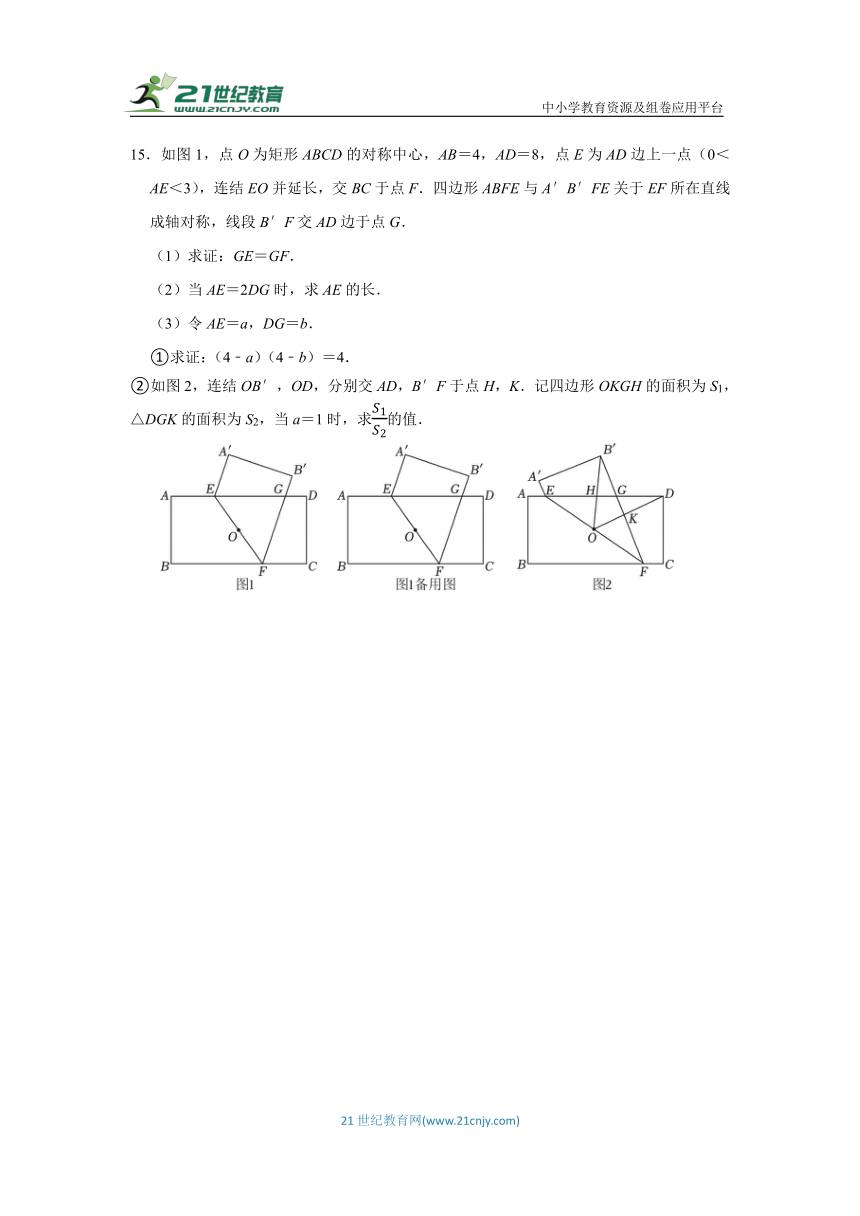
15.如图1,点O为矩形ABCD的对称中心,AB=4,AD=8,点E为AD边上一点(0<AE<3),连结EO并延长,交BC于点F.四边形ABFE与A′B′FE关于EF所在直线成轴对称,线段B′F交AD边于点G.
(1)求证:GE=GF.
(2)当AE=2DG时,求AE的长.
(3)令AE=a,DG=b.
①求证:(4﹣a)(4﹣b)=4.
②如图2,连结OB′,OD,分别交AD,B′F于点H,K.记四边形OKGH的面积为S1,△DGK的面积为S2,当a=1时,求的值.
参考答案
一、选择题
题号 1 2 3 4 5
答案 C B D D A
二、填空题
6.【解答】解:作OH∥BC交CD于点H,则△DOH∽△DBC,
∵四边形ABCD是边长为10的菱形,对角线AC,BD相交于点O,
∴BC=10,OD=OBBD,OA=OC,AC⊥BD,
∴,∠BOC=90°,
∴OHBC=5,
∵OH∥EC,,
∴△OFH∽△EFC,
∴,
∴ECOH5=6,
∵BC=DC,AC⊥BD,∠ACD=2∠OEC,
∴∠ACB=∠ACD=2∠OEC=∠COE+∠OEC,
∴∠OEC=∠COE,
∴OC=EC=6,
∴OB8,
∴BD=2OB=16,AC=2OC=12,
∴S菱形ABCDBD AC16×12=96,
故答案为:96.
7.【解答】解:方法一:如图,延长CD到点G,使DG=BM.
∵四边形ABCD为正方形,
∴AD=BC=AB,∠BAD=∠ADC=90°,
∴∠ADG=∠ADN=90°=∠ABM,
又∵BM=DG,AD=AB,
∴△ABM≌△ADG(SAS),
∴∠BAM=∠DAG,AM=AG,
∵∠MAN=45°,
∴∠BAM+∠DAN=45°,
∴∠DAG+∠DAN=45°,即∠GAN=45°,
在△GAN和△MAN中,
,
∴△GAN≌△MAN(SAS),
∴GN=MN.
设BM=x,MN=y,则GN=y,DG=x.
∵BC=CD=1,
∴CM=1﹣x,CN=x﹣y+1,
在Rt△CMN中,由勾股定理得:MN2=CM2+CN2,
即y2=(1﹣x)2+(x﹣y+1)2,
整理可得:yx+12,
∵x+122,
∴y≥22,
当x1时,y最小值为22.
方法二:如图,延长CD到点G,使DG=BM.
∵四边形ABCD为正方形,
∴AD=BC=AB,∠BAD=∠ADC=90°,
∴∠ADG=∠ADN=90°=∠ABM,
又∵BM=DG,AD=AB,
∴△ABM≌△ADG(SAS),
∴∠BAM=∠DAG,AM=AG,
∵∠MAN=45°,
∴∠BAM+∠DAN=45°,
∴∠DAG+∠DAN=45°,即∠GAN=45°,
在△GAN和△MAN中,
,
∴△GAN≌△MAN(SAS),
∴GN=MN.
作△GAN的外接圆,圆心为O,
∵∠GAN=45°,
∴∠GON=90°,
过O作OH⊥GN于点H,则GH=NH,
设GH=NH=a,则GN=2a,OH=a,
在Rt△GON中,OG=ONa,
∴OAa,
∵OA+OH≥AD,
∴a+a≥1,
∴a1,
当A、O、H三点共线时取等,
此时GN=2a=2,
∴MN=2;
故MN的最小值为:22.
8.【解答】解:(Ⅰ)∵四边形ABCD是正方形,
∴OA=OC=OD=OB,∠DOC=90°,
∴在Rt△DOC中,OD2+OC2=DC2,
∵DC=3,
∴OA=OD=OC=OB=3,
∵OE=5,
∴AE=OE﹣OA=2;
故答案为:2.
(Ⅱ)延长DA到点G,使AG=AD,连接EG,过E作EH⊥AG于H,
∵F为DE中点,A为DG中点,
∴AF为△DGE中位线,
∴AFEG,
在Rt△EAH中,∠EAH=∠DAC=45°,
∴AH=EH,
∵AH2+EH2=AE2,
∴AH=EH,
∴GH=AG﹣AH=32,
在Rt△EGH中,EG2=EH2+GH2=10,
∴EG,
∴AFEG.
故答案为:.
9.【解答】解:(1)过E作EM⊥AD于M,
∵EA=ED.AD=3,
∴AM=DMAD,
∴EM2,
∴△ADE的面积为3×2=3;
故答案为:3;
(2)过E作AD的垂线交AD于M,AG于N,BC于P,
∵四边形ABCD是正方形,
∴BC∥AD,
∴EP⊥BC,
∴四边形ABPM是矩形,
∴PM=AB=3,AB∥EP,
∴EP=5,∠ABF=∠NEF,
∵F为BE的中点,
∴BF=EF,
在△ABF与△NEF中,
,
∴△ABF≌△NEF(ASA),
∴EN=AB=3,
∴MN=1,
∵PM∥CD,
∴AN=NG,
∴GD=2MN=2,
∴AG,
故答案为:.
10.【解答】解:连接OE,
∵四边形ABCD是矩形,
∴∠ABC=90°,BC=AD=12,AO=CO=BO=DO,
∵AB=5,BC=12,
∴AC13,
∴OB=OC,
∴S△BOC=S△BOE+S△COEOB EGOC EFS△ABC15,
∴,
∴EG+EF,
故答案为:.
【点评】此题考查了矩形的性质、勾股定理.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.
三、解答题
11.如图,在四边形ABCD中,E是AB的中点,DB,CE交于点F,DF=FB,AF∥DC.
(1)求证:四边形AFCD为平行四边形;
(2)若∠EFB=90°,tan∠FEB=3,EF=1,求BC的长.
【分析】(1)根据三角形中位线定理得到EF∥AD,根据平行四边形的判定定理得到结论;
(2)根据三角形中位线定理求得AD=2EF=2,根据三角函数的定义得到BF=3EF=3,求得DF=BF=3,根据勾股定理得到AF,根据平行四边形的性质得到CD=AF,根据线段垂直平分线的性质得到结论.
【解答】(1)证明:∵E是AB的中点,
∴AE=BE,
∵DF=BF,
∴EF是△ABD的中位线,
∴EF∥AD,
∴CF∥AD,
∵AF∥CD,
∴四边形AFCD为平行四边形;
(2)解:由(1)知,EF是△ABD的中位线,
∴AD=2EF=2,
∵∠EFB=90°,tan∠FEB=3,
∴BF=3EF=3,
∵DF=FB,
∴DF=BF=3,
∵AD∥CE,
∴∠ADF=∠EFB=90°,
∴AF,
∵四边形AFCD为平行四边形,
∴CD=AF,
∵DF=BF,CE⊥BD,
∴BC=CD.
12.如图,在菱形ABCD中,AB=10cm,∠ABC=60°,E为对角线AC上一动点,以DE为一边作∠DEF=60°,EF交射线BC于点F,连接BE,DF.点E从点C出发,沿CA方向以每秒2cm的速度运动至点A处停止.设△BEF的面积为y cm2,点E的运动时间为x秒.
(1)求证:BE=EF;
(2)求y与x的函数表达式,并写出自变量x的取值范围;
(3)求x为何值时,线段DF的长度最短.
【分析】(1)设CD与EF相交于点M,证明△BCE≌△DCE(SAS),可得∠CBE=∠CDE,BE=DE,利用三角形外角性质可得∠CDE=∠CFE,即得∠CBE=∠CFE,即可求证;
(2)过点E作EN⊥BC于N,解直角三角形得到EN=CE sin60°,CN=CE cos60°,可得BN=BC﹣CN,由等腰三角形三线合一可得BF,即可由三角形面积公式得到y与x的函数表达式,最后由0<2x≤10,可得自变量x的取值范围;
(3)证明△DEF为等边三角形,可得BE=DF,可知线段DF的长度最短,即BE的长度最短,当BE⊥AC时,BE取最短,又由菱形的性质可得△ABC为等边三角形,利用三线合一求出CE即可求解;
【解答】(1)证明:设CD与EF相交于点M,
∵四边形ABCD为菱形,∴BC﹣=DC,∠BCE=∠DCE,AB∥CD,
∵∠ABC=60°,
∴∠DCF=60°,
在△BCE和△DCE中,
,
∴△BCE≌△DCE(SAS),
∴∠CBE=∠CDE,BE=DE,
∵∠DMF=∠DEF+∠CDE=∠DCF+∠CFE,
又∵∠DEF=∠DCF=60°,
∴∠CDE=∠CFE,
∴∠CBE=∠CFE,
∴BE=EF;
(2)解:过点E作EN⊥BC于N,
则∠ENC=90°,
∵BE=EF,
∴BF=2BN,
∵四边形ABCD为菱形,∠ABC=60°,
∴BC=AB=10cm,∠ACB=∠BCD=60°,即∠ECN=60°,
∵CE=2x cm,
∴EN=CE sin60°=2x x(cm),CN=CE cos60°=2x x(cm),
∴BN=BC﹣CN=10﹣x(cm),
∴BF=2(10﹣x)cm,
∴yBF EN2(10﹣x)xx2+10x,
∵0<2x≤10,
∴0<x≤5,
∴yx2+10x(0<x≤5);
(3)解:∵BE=DE,BE=EF,
∴DE=EF,
∵∠DEF=60°,
∴△DEF为等边三角形,
∴DE=DF﹣EF,
∴BE=DF,
∴线段DF的长度最短,即BE的长度最短,当BE⊥AC时,BE取最短,如图,
∵四边形ABCD是菱形,
∴AD=BC,
∵∠ABC=60°,
∴△ABC为等边三角形,
∴AE=AB=AC=10cm,
∵BE⊥AC,
∴CEAC=5cm,
∴x,
∴当x时,线段DF的长度最短.
13.如图,在菱形ABCD中,对角线AC,BD相交于点O,点P,Q分别是边BC,线段OD上的点,连接AP,QP,AP与OB相交于点E.
(1)如图1,连接QA.当QA=QP时,试判断点Q是否在线段PC的垂直平分线上,并说明理由;
(2)如图2,若∠APB=90°,且∠BAP=∠ADB,
①求证:AE=2EP;
②当OQ=OE时,设EP=a,求PQ的长(用含a的代数式表示).
【分析】(1)根据菱形的性质及垂直平分线的判定证明即可;
(2)①根据菱形的性质得出AB=BC=CD=DA,再由各角之间的关系得出∠BAP=∠ABD=∠CBD=30°,由含30度角的直角三角形的性质求解即可;
②连接QC.利用等边三角形的判定和性质得出AE=2a,AP=3a,再由正切函数及全等三角形的判定和性质及勾股定理求解即可.
【解答】(1)解:结论:点Q在线段PC的垂直平分线上.
理由:连接QC.∵四边形ABCD是菱形,对角线AC,BD相交于点O,
∴BD⊥AC,OA=OC,
∴QA=QC,
∵QA=QP,
∴QC=QP,
∴点Q在线段PC的垂直平分线上;
(2)①证明:如图,∵四边形ABCD是菱形,
∴AB=BC=CD=DA,
∴∠ABD=∠ADB,∠CBD=∠CDB,
∵BD⊥AC,∴∠ADO=∠CDO,
∴∠ABD=∠CBD=∠ADO.
∵∠BAP=∠ADB,
∴∠BAP=∠ABD=∠CBD.
∴AE=BE,∠APB=90°,∠BAP+∠ABP=90°,∠BAP=∠ABD=∠CBD=30°
在 Rt△BPE 中,∠EPB=90°,∠PBE=30°,
∴EPBE,
∵AE=BE,
∴,
∴AE=2EP;
②如图,连接QC.
∵AB=BC,∠ABC=60°,
∴△ABC 是等边三角形.∠APB=90°,
∴BP=CP,EP=a,
∴AE=2a,AP=3a,
在Rt△APB中,∠APB=90°,
∵,
∴,
∴,
∵AO=CO,∠AOE=∠COQ,OE=OQ,
△AOE≌△COQ(SAS),
∴AE=CQ=2a,∠EAO=∠QCO,
∴AE∥CQ,
∵∠APB=90°,
∴∠QCP=90°,
在Rt△PCQ中,∠QCP=90°,
由勾股定理得 PQ2=PC2+CQ2,
∴PQ2=PC2+CQ2,
∴PQa.
14.如图,在正方形ABCD中,线段CD绕点C逆时针旋转到CE处,旋转角为α,点F在直线DE上,且AD=AF,连接BF.
(1)如图1,当0°<α<90°时,
①求∠BAF的大小(用含α的式子表示).
②求证:EFBF.
(2)如图2,取线段EF的中点G,连接AG,已知AB=2,请直接写出在线段CE旋转过程中(0°<α<360°)△ADG面积的最大值.
【分析】(1)①利用等腰三角形的性质,三角形内角和定理计算得到∠FAD=180°﹣α,据此求解即可;
②连接BE,计算得到∠BCE=90°﹣α=∠BAF,利用SAS证明△BCE≌△BAF,推出△EBF是等腰直角三角形,据此即可证明EFBF;
(2)过点G作AD的垂直,交直线AD于点H,连接AC,BD相交于点,连接OG,利用直角三角形的性质推出点G在以点O为圆心,OB为半径的一段弧上,得到当点H、O、G在同一直线上时,GH有最大值,则△ADG面积的最大值,据此求解即可.
【解答】(1)解:①∵四边形ABCD是正方形,
∴AB=BC=CD=DA.∠ADC=∠BCD=∠DAB=90°,
由题意得CD=CE,∠DCE=α:
∴∠CDE=∠CED(180°﹣α)=90°α.
∴∠ADF=90°﹣∠CDE=90°﹣(90°α)α,
∵AD=AF,
∴∠ADF=∠AFDα,
∴∠FAD=180°﹣∠ADF﹣∠AFD=180°﹣α,
∴∠BAF=∠FAD﹣∠BAD=180°﹣α﹣90°=90°﹣α;
②连接BE.
∵∠DCE=α,
∴∠BCE﹣90°﹣α=∠BAF,
∵CD=CE=AD=AF=BC,
∴△BCE≌△BAF(SAS),
∴BF=BE,∠ABF=∠CBE.
∵∠ABC=90°,
∴∠EBF=90°
∴△EBF是等腰直角三角形,
∴EFBF;
(2)解:过点G作AD的垂线,交直线AD于点H,连接AC,BD相交于点,O,连接OG,
由(1)得△EBF是等腰直角三角形,又点G为斜边EF的中点,
∴BG⊥EF,即∠BGD=90°,
∵四边形ABCD是正方形,
∴OB=OD.
∴OB=OD=OG,
∴点G在以点O为圆心,OB为半径的一段弧上,
当点H、O、G在同一直线上时,GH有最大值,则△ADG面积的最大值,
∴GHAB+OGABBD221.
∴△ADG面积的最大值为AD×GH=1.
15.如图1,点O为矩形ABCD的对称中心,AB=4,AD=8,点E为AD边上一点(0<AE<3),连结EO并延长,交BC于点F.四边形ABFE与A′B′FE关于EF所在直线成轴对称,线段B′F交AD边于点G.
(1)求证:GE=GF.
(2)当AE=2DG时,求AE的长.
(3)令AE=a,DG=b.
①求证:(4﹣a)(4﹣b)=4.
②如图2,连结OB′,OD,分别交AD,B′F于点H,K.记四边形OKGH的面积为S1,△DGK的面积为S2,当a=1时,求的值.
【分析】(1)由四边形ABCD是矩形,可得∠GEF=∠BFE,而四边形ABFE与A′B′FE关于EF所在直线成轴对称,有∠BFE=∠GFE,故∠GEF=∠GFE,GE=GF;
(2)过G作GH⊥BC于H,设DG=x,可知AE=2x,GE=AD﹣AE﹣DG=8﹣3x=GF,根据点O为矩形ABCD的对称中心,可得CF=AE=2x,故FH=CF﹣CH=x,在Rt△GFH中,x2+42=(8﹣3x)2,解得x的值从而可得AE的长为6﹣2;
(3)①过O作OQ⊥AD于Q,连接OA,OD,OG,由点O为矩形ABCD的对称中心,EF过点O,可得O为EF中点,OA=OD,OQAB=2,证明△GOQ∽△OEQ,得,即GQ EQ=OQ2,故GQ EQ=4,即可得(4﹣a)(4﹣b)=4;
②连接B'D,OG,OB,证明B'F=DE,OD=OB=OB',可得△DOG≌△B'OG(SSS),∠ODG=∠OB'G,从而△DGK≌△B'GH(ASA),DK=B'H,GK=GH,即可证△OGK≌△OGH(SSS),得S△OGK=S△OGH,有,而∠EGF=∠DGB',GE=GF,GD=GB',知EF∥B'D,可得△OKF∽△DKB',△EGF∽△DGB',得,,又△EGF∽△DGB',有,当a=1时,b,即AE=1,DG,即可得.
【解答】(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠GEF=∠BFE,
∵四边形ABFE与A′B′FE关于EF所在直线成轴对称,
∴∠BFE=∠GFE,
∴∠GEF=∠GFE,
∴GE=GF;
(2)解:过G作GH⊥BC于H,如图:
设DG=x,则AE=2x,
∴GE=AD﹣AE﹣DG=8﹣3x=GF,
∵∠GHC=∠C=∠D=90°,
∴四边形GHCD是矩形,
∴GH=CD=AB=4,CH=DG=x,
∵点O为矩形ABCD的对称中心,
∴CF=AE=2x,
∴FH=CF﹣CH=x,
在Rt△GFH中,FH2+GH2=GF2,
∴x2+42=(8﹣3x)2,
解得x=3(此时AE大于AD,舍去)或x=3,
∴AE=2x=6﹣2;
∴AE的长为6﹣2;
(3)①证明:过O作OQ⊥AD于Q,连接OA,OD,OG,如图:
∵点O为矩形ABCD的对称中心,EF过点O,
∴O为EF中点,OA=OD,OQAB=2,
∵GE=GF,
∴OG⊥EF,
∴∠GOQ=90°﹣∠EOQ=∠QEO,
∵∠GQO=90°=∠OQE,
∴△GOQ∽△OEQ,
∴,即GQ EQ=OQ2,
∴GQ EQ=4,
∵OA=OD,OQ⊥AD,
∴AQ=DQAD=4,
∴EQ=AQ﹣AE=4﹣a,GQ=DQ﹣GD=4﹣b,
∴(4﹣a)(4﹣b)=4;
②解:连接B'D,OG,OB,如图:
∵四边形ABFE与A′B′FE关于EF所在直线成轴对称,
∴BF=B'F,
∵点O为矩形ABCD的对称中心,
∴BF=DE,
∴B'F=DE,
同理OD=OB=OB',
由(1)知GF=GE,
∴B'F﹣GF=DE﹣GE,即B'G=DG,
∵OG=OG,
∴△DOG≌△B'OG(SSS),
∴∠ODG=∠OB'G,
∵DG=B'G,∠DGK=∠B'GH,
∴△DGK≌△B'GH(ASA),
∴DK=B'H,GK=GH,
∴OD﹣DK=OB'﹣B'H,即OK=OH,
∵OG=OG,
∴△OGK≌△OGH(SSS),
∴S△OGK=S△OGH,
∴S1=2S△OGK,
∴,
∵∠EGF=∠DGB',GE=GF,GD=GB',
∴∠GEF=∠GFE=∠GDB'=∠GB'D,
∴EF∥B'D,
∴△OKF∽△DKB',△EGF∽△DGB',
∴,
∵,
∴,
∵△EGF∽△DGB',
∴,
当a=1时,由①知(4﹣1)×(4﹣b)=4,
∴b,
∴AE=1,DG,
∴GE=AD﹣AE﹣DG,
∴,
∴的值为.
21世纪教育网(www.21cnjy.com)
2025年九年级数学中考三轮冲刺练习四边形压轴题综合训练
一、选择题
1.如图,在 ABCD中,AC,BD相交于点O,AC=2,.过点A作AE⊥BC的垂线交BC于点E,记BE长为x,BC长为y.当x,y的值发生变化时,下列代数式的值不变的是( )
A.x+y B.x﹣y C.xy D.x2+y2
2.如图,在Rt△ABC中,∠C=90°,AC=12,BC=5,点P是边AB上任意一点,过点P作PD⊥AC,PE⊥BC,垂足分别为点D,E,连接DE,则DE的最小值是( )
A. B. C. D.
3.如图,矩形ABCD中,AB,BC=1,动点E,F分别从点A,C同时出发,以每秒1个单位长度的速度沿AB,CD向终点B,D运动,过点E,F作直线l,过点A作直线l的垂线,垂足为G,则AG的最大值为( )
A. B. C.2 D.1
4.如图,在边长为4的正方形ABCD中,点E是BC上一点,点F是CD延长线上一点,连接AE,AF,AM平分∠EAF交CD于点M.若BE=DF=1,则DM的长度为( )
A.2 B. C. D.
5.如图,在正方形ABCD中,点H在AD边上(不与点A、D重合),∠BHF=90°,HF交正方形外角的平分线DF于点F,连接AC交BH于点M,连接BF交AC于点G,交CD于点N,连接BD.则下列结论:
①∠HBF=45°;②点G是BF的中点;③若点H是AD的中点,则sin∠NBC;④BNBM;⑤若AHHD,则S△BNDS△AHM.其中正确的结论是( )
A.①②③④ B.①③⑤ C.①②④⑤ D.①②③④⑤
二、填空题
6.如图,在边长为10的菱形ABCD中,对角线AC,BD相交于点O,点E在BC延长线上,OE与CD相交于点F.若∠ACD=2∠OEC,,则菱形ABCD的面积为 .
7.如图,正方形ABCD的边长为1,M、N是边BC、CD上的动点.若∠MAN=45°,则MN的最小值为 .
8.如图,正方形ABCD的边长为,对角线AC,BD相交于点O,点E在CA的延长线上,OE=5,连接DE.
(Ⅰ)线段AE的长为 ;
(Ⅱ)若F为DE的中点,则线段AF的长为 .
9.如图,在边长为3的正方形ABCD的外侧,作等腰三角形ADE,EA=ED.
(1)△ADE的面积为 ;
(2)若F为BE的中点,连接AF并延长,与CD相交于点G,则AG的长为 .
10.出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建.“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一,如图,在矩形ABCD中,AB=5,AD=12,对角线AC与BD交于点O,点E为BC边上的一个动点,EF⊥AC,EG⊥BD,垂足分别为点F,G,则EF+EG= .
三、解答题
11.如图,在四边形ABCD中,E是AB的中点,DB,CE交于点F,DF=FB,AF∥DC.
(1)求证:四边形AFCD为平行四边形;
(2)若∠EFB=90°,tan∠FEB=3,EF=1,求BC的长.
12.如图,在菱形ABCD中,AB=10cm,∠ABC=60°,E为对角线AC上一动点,以DE为一边作∠DEF=60°,EF交射线BC于点F,连接BE,DF.点E从点C出发,沿CA方向以每秒2cm的速度运动至点A处停止.设△BEF的面积为y cm2,点E的运动时间为x秒.
(1)求证:BE=EF;
(2)求y与x的函数表达式,并写出自变量x的取值范围;
(3)求x为何值时,线段DF的长度最短.
13.如图,在菱形ABCD中,对角线AC,BD相交于点O,点P,Q分别是边BC,线段OD上的点,连接AP,QP,AP与OB相交于点E.
(1)如图1,连接QA.当QA=QP时,试判断点Q是否在线段PC的垂直平分线上,并说明理由;
(2)如图2,若∠APB=90°,且∠BAP=∠ADB,
①求证:AE=2EP;
②当OQ=OE时,设EP=a,求PQ的长(用含a的代数式表示).
14.如图,在正方形ABCD中,线段CD绕点C逆时针旋转到CE处,旋转角为α,点F在直线DE上,且AD=AF,连接BF.
(1)如图1,当0°<α<90°时,
①求∠BAF的大小(用含α的式子表示).
②求证:EFBF.
(2)如图2,取线段EF的中点G,连接AG,已知AB=2,请直接写出在线段CE旋转过程中(0°<α<360°)△ADG面积的最大值.
15.如图1,点O为矩形ABCD的对称中心,AB=4,AD=8,点E为AD边上一点(0<AE<3),连结EO并延长,交BC于点F.四边形ABFE与A′B′FE关于EF所在直线成轴对称,线段B′F交AD边于点G.
(1)求证:GE=GF.
(2)当AE=2DG时,求AE的长.
(3)令AE=a,DG=b.
①求证:(4﹣a)(4﹣b)=4.
②如图2,连结OB′,OD,分别交AD,B′F于点H,K.记四边形OKGH的面积为S1,△DGK的面积为S2,当a=1时,求的值.
参考答案
一、选择题
题号 1 2 3 4 5
答案 C B D D A
二、填空题
6.【解答】解:作OH∥BC交CD于点H,则△DOH∽△DBC,
∵四边形ABCD是边长为10的菱形,对角线AC,BD相交于点O,
∴BC=10,OD=OBBD,OA=OC,AC⊥BD,
∴,∠BOC=90°,
∴OHBC=5,
∵OH∥EC,,
∴△OFH∽△EFC,
∴,
∴ECOH5=6,
∵BC=DC,AC⊥BD,∠ACD=2∠OEC,
∴∠ACB=∠ACD=2∠OEC=∠COE+∠OEC,
∴∠OEC=∠COE,
∴OC=EC=6,
∴OB8,
∴BD=2OB=16,AC=2OC=12,
∴S菱形ABCDBD AC16×12=96,
故答案为:96.
7.【解答】解:方法一:如图,延长CD到点G,使DG=BM.
∵四边形ABCD为正方形,
∴AD=BC=AB,∠BAD=∠ADC=90°,
∴∠ADG=∠ADN=90°=∠ABM,
又∵BM=DG,AD=AB,
∴△ABM≌△ADG(SAS),
∴∠BAM=∠DAG,AM=AG,
∵∠MAN=45°,
∴∠BAM+∠DAN=45°,
∴∠DAG+∠DAN=45°,即∠GAN=45°,
在△GAN和△MAN中,
,
∴△GAN≌△MAN(SAS),
∴GN=MN.
设BM=x,MN=y,则GN=y,DG=x.
∵BC=CD=1,
∴CM=1﹣x,CN=x﹣y+1,
在Rt△CMN中,由勾股定理得:MN2=CM2+CN2,
即y2=(1﹣x)2+(x﹣y+1)2,
整理可得:yx+12,
∵x+122,
∴y≥22,
当x1时,y最小值为22.
方法二:如图,延长CD到点G,使DG=BM.
∵四边形ABCD为正方形,
∴AD=BC=AB,∠BAD=∠ADC=90°,
∴∠ADG=∠ADN=90°=∠ABM,
又∵BM=DG,AD=AB,
∴△ABM≌△ADG(SAS),
∴∠BAM=∠DAG,AM=AG,
∵∠MAN=45°,
∴∠BAM+∠DAN=45°,
∴∠DAG+∠DAN=45°,即∠GAN=45°,
在△GAN和△MAN中,
,
∴△GAN≌△MAN(SAS),
∴GN=MN.
作△GAN的外接圆,圆心为O,
∵∠GAN=45°,
∴∠GON=90°,
过O作OH⊥GN于点H,则GH=NH,
设GH=NH=a,则GN=2a,OH=a,
在Rt△GON中,OG=ONa,
∴OAa,
∵OA+OH≥AD,
∴a+a≥1,
∴a1,
当A、O、H三点共线时取等,
此时GN=2a=2,
∴MN=2;
故MN的最小值为:22.
8.【解答】解:(Ⅰ)∵四边形ABCD是正方形,
∴OA=OC=OD=OB,∠DOC=90°,
∴在Rt△DOC中,OD2+OC2=DC2,
∵DC=3,
∴OA=OD=OC=OB=3,
∵OE=5,
∴AE=OE﹣OA=2;
故答案为:2.
(Ⅱ)延长DA到点G,使AG=AD,连接EG,过E作EH⊥AG于H,
∵F为DE中点,A为DG中点,
∴AF为△DGE中位线,
∴AFEG,
在Rt△EAH中,∠EAH=∠DAC=45°,
∴AH=EH,
∵AH2+EH2=AE2,
∴AH=EH,
∴GH=AG﹣AH=32,
在Rt△EGH中,EG2=EH2+GH2=10,
∴EG,
∴AFEG.
故答案为:.
9.【解答】解:(1)过E作EM⊥AD于M,
∵EA=ED.AD=3,
∴AM=DMAD,
∴EM2,
∴△ADE的面积为3×2=3;
故答案为:3;
(2)过E作AD的垂线交AD于M,AG于N,BC于P,
∵四边形ABCD是正方形,
∴BC∥AD,
∴EP⊥BC,
∴四边形ABPM是矩形,
∴PM=AB=3,AB∥EP,
∴EP=5,∠ABF=∠NEF,
∵F为BE的中点,
∴BF=EF,
在△ABF与△NEF中,
,
∴△ABF≌△NEF(ASA),
∴EN=AB=3,
∴MN=1,
∵PM∥CD,
∴AN=NG,
∴GD=2MN=2,
∴AG,
故答案为:.
10.【解答】解:连接OE,
∵四边形ABCD是矩形,
∴∠ABC=90°,BC=AD=12,AO=CO=BO=DO,
∵AB=5,BC=12,
∴AC13,
∴OB=OC,
∴S△BOC=S△BOE+S△COEOB EGOC EFS△ABC15,
∴,
∴EG+EF,
故答案为:.
【点评】此题考查了矩形的性质、勾股定理.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.
三、解答题
11.如图,在四边形ABCD中,E是AB的中点,DB,CE交于点F,DF=FB,AF∥DC.
(1)求证:四边形AFCD为平行四边形;
(2)若∠EFB=90°,tan∠FEB=3,EF=1,求BC的长.
【分析】(1)根据三角形中位线定理得到EF∥AD,根据平行四边形的判定定理得到结论;
(2)根据三角形中位线定理求得AD=2EF=2,根据三角函数的定义得到BF=3EF=3,求得DF=BF=3,根据勾股定理得到AF,根据平行四边形的性质得到CD=AF,根据线段垂直平分线的性质得到结论.
【解答】(1)证明:∵E是AB的中点,
∴AE=BE,
∵DF=BF,
∴EF是△ABD的中位线,
∴EF∥AD,
∴CF∥AD,
∵AF∥CD,
∴四边形AFCD为平行四边形;
(2)解:由(1)知,EF是△ABD的中位线,
∴AD=2EF=2,
∵∠EFB=90°,tan∠FEB=3,
∴BF=3EF=3,
∵DF=FB,
∴DF=BF=3,
∵AD∥CE,
∴∠ADF=∠EFB=90°,
∴AF,
∵四边形AFCD为平行四边形,
∴CD=AF,
∵DF=BF,CE⊥BD,
∴BC=CD.
12.如图,在菱形ABCD中,AB=10cm,∠ABC=60°,E为对角线AC上一动点,以DE为一边作∠DEF=60°,EF交射线BC于点F,连接BE,DF.点E从点C出发,沿CA方向以每秒2cm的速度运动至点A处停止.设△BEF的面积为y cm2,点E的运动时间为x秒.
(1)求证:BE=EF;
(2)求y与x的函数表达式,并写出自变量x的取值范围;
(3)求x为何值时,线段DF的长度最短.
【分析】(1)设CD与EF相交于点M,证明△BCE≌△DCE(SAS),可得∠CBE=∠CDE,BE=DE,利用三角形外角性质可得∠CDE=∠CFE,即得∠CBE=∠CFE,即可求证;
(2)过点E作EN⊥BC于N,解直角三角形得到EN=CE sin60°,CN=CE cos60°,可得BN=BC﹣CN,由等腰三角形三线合一可得BF,即可由三角形面积公式得到y与x的函数表达式,最后由0<2x≤10,可得自变量x的取值范围;
(3)证明△DEF为等边三角形,可得BE=DF,可知线段DF的长度最短,即BE的长度最短,当BE⊥AC时,BE取最短,又由菱形的性质可得△ABC为等边三角形,利用三线合一求出CE即可求解;
【解答】(1)证明:设CD与EF相交于点M,
∵四边形ABCD为菱形,∴BC﹣=DC,∠BCE=∠DCE,AB∥CD,
∵∠ABC=60°,
∴∠DCF=60°,
在△BCE和△DCE中,
,
∴△BCE≌△DCE(SAS),
∴∠CBE=∠CDE,BE=DE,
∵∠DMF=∠DEF+∠CDE=∠DCF+∠CFE,
又∵∠DEF=∠DCF=60°,
∴∠CDE=∠CFE,
∴∠CBE=∠CFE,
∴BE=EF;
(2)解:过点E作EN⊥BC于N,
则∠ENC=90°,
∵BE=EF,
∴BF=2BN,
∵四边形ABCD为菱形,∠ABC=60°,
∴BC=AB=10cm,∠ACB=∠BCD=60°,即∠ECN=60°,
∵CE=2x cm,
∴EN=CE sin60°=2x x(cm),CN=CE cos60°=2x x(cm),
∴BN=BC﹣CN=10﹣x(cm),
∴BF=2(10﹣x)cm,
∴yBF EN2(10﹣x)xx2+10x,
∵0<2x≤10,
∴0<x≤5,
∴yx2+10x(0<x≤5);
(3)解:∵BE=DE,BE=EF,
∴DE=EF,
∵∠DEF=60°,
∴△DEF为等边三角形,
∴DE=DF﹣EF,
∴BE=DF,
∴线段DF的长度最短,即BE的长度最短,当BE⊥AC时,BE取最短,如图,
∵四边形ABCD是菱形,
∴AD=BC,
∵∠ABC=60°,
∴△ABC为等边三角形,
∴AE=AB=AC=10cm,
∵BE⊥AC,
∴CEAC=5cm,
∴x,
∴当x时,线段DF的长度最短.
13.如图,在菱形ABCD中,对角线AC,BD相交于点O,点P,Q分别是边BC,线段OD上的点,连接AP,QP,AP与OB相交于点E.
(1)如图1,连接QA.当QA=QP时,试判断点Q是否在线段PC的垂直平分线上,并说明理由;
(2)如图2,若∠APB=90°,且∠BAP=∠ADB,
①求证:AE=2EP;
②当OQ=OE时,设EP=a,求PQ的长(用含a的代数式表示).
【分析】(1)根据菱形的性质及垂直平分线的判定证明即可;
(2)①根据菱形的性质得出AB=BC=CD=DA,再由各角之间的关系得出∠BAP=∠ABD=∠CBD=30°,由含30度角的直角三角形的性质求解即可;
②连接QC.利用等边三角形的判定和性质得出AE=2a,AP=3a,再由正切函数及全等三角形的判定和性质及勾股定理求解即可.
【解答】(1)解:结论:点Q在线段PC的垂直平分线上.
理由:连接QC.∵四边形ABCD是菱形,对角线AC,BD相交于点O,
∴BD⊥AC,OA=OC,
∴QA=QC,
∵QA=QP,
∴QC=QP,
∴点Q在线段PC的垂直平分线上;
(2)①证明:如图,∵四边形ABCD是菱形,
∴AB=BC=CD=DA,
∴∠ABD=∠ADB,∠CBD=∠CDB,
∵BD⊥AC,∴∠ADO=∠CDO,
∴∠ABD=∠CBD=∠ADO.
∵∠BAP=∠ADB,
∴∠BAP=∠ABD=∠CBD.
∴AE=BE,∠APB=90°,∠BAP+∠ABP=90°,∠BAP=∠ABD=∠CBD=30°
在 Rt△BPE 中,∠EPB=90°,∠PBE=30°,
∴EPBE,
∵AE=BE,
∴,
∴AE=2EP;
②如图,连接QC.
∵AB=BC,∠ABC=60°,
∴△ABC 是等边三角形.∠APB=90°,
∴BP=CP,EP=a,
∴AE=2a,AP=3a,
在Rt△APB中,∠APB=90°,
∵,
∴,
∴,
∵AO=CO,∠AOE=∠COQ,OE=OQ,
△AOE≌△COQ(SAS),
∴AE=CQ=2a,∠EAO=∠QCO,
∴AE∥CQ,
∵∠APB=90°,
∴∠QCP=90°,
在Rt△PCQ中,∠QCP=90°,
由勾股定理得 PQ2=PC2+CQ2,
∴PQ2=PC2+CQ2,
∴PQa.
14.如图,在正方形ABCD中,线段CD绕点C逆时针旋转到CE处,旋转角为α,点F在直线DE上,且AD=AF,连接BF.
(1)如图1,当0°<α<90°时,
①求∠BAF的大小(用含α的式子表示).
②求证:EFBF.
(2)如图2,取线段EF的中点G,连接AG,已知AB=2,请直接写出在线段CE旋转过程中(0°<α<360°)△ADG面积的最大值.
【分析】(1)①利用等腰三角形的性质,三角形内角和定理计算得到∠FAD=180°﹣α,据此求解即可;
②连接BE,计算得到∠BCE=90°﹣α=∠BAF,利用SAS证明△BCE≌△BAF,推出△EBF是等腰直角三角形,据此即可证明EFBF;
(2)过点G作AD的垂直,交直线AD于点H,连接AC,BD相交于点,连接OG,利用直角三角形的性质推出点G在以点O为圆心,OB为半径的一段弧上,得到当点H、O、G在同一直线上时,GH有最大值,则△ADG面积的最大值,据此求解即可.
【解答】(1)解:①∵四边形ABCD是正方形,
∴AB=BC=CD=DA.∠ADC=∠BCD=∠DAB=90°,
由题意得CD=CE,∠DCE=α:
∴∠CDE=∠CED(180°﹣α)=90°α.
∴∠ADF=90°﹣∠CDE=90°﹣(90°α)α,
∵AD=AF,
∴∠ADF=∠AFDα,
∴∠FAD=180°﹣∠ADF﹣∠AFD=180°﹣α,
∴∠BAF=∠FAD﹣∠BAD=180°﹣α﹣90°=90°﹣α;
②连接BE.
∵∠DCE=α,
∴∠BCE﹣90°﹣α=∠BAF,
∵CD=CE=AD=AF=BC,
∴△BCE≌△BAF(SAS),
∴BF=BE,∠ABF=∠CBE.
∵∠ABC=90°,
∴∠EBF=90°
∴△EBF是等腰直角三角形,
∴EFBF;
(2)解:过点G作AD的垂线,交直线AD于点H,连接AC,BD相交于点,O,连接OG,
由(1)得△EBF是等腰直角三角形,又点G为斜边EF的中点,
∴BG⊥EF,即∠BGD=90°,
∵四边形ABCD是正方形,
∴OB=OD.
∴OB=OD=OG,
∴点G在以点O为圆心,OB为半径的一段弧上,
当点H、O、G在同一直线上时,GH有最大值,则△ADG面积的最大值,
∴GHAB+OGABBD221.
∴△ADG面积的最大值为AD×GH=1.
15.如图1,点O为矩形ABCD的对称中心,AB=4,AD=8,点E为AD边上一点(0<AE<3),连结EO并延长,交BC于点F.四边形ABFE与A′B′FE关于EF所在直线成轴对称,线段B′F交AD边于点G.
(1)求证:GE=GF.
(2)当AE=2DG时,求AE的长.
(3)令AE=a,DG=b.
①求证:(4﹣a)(4﹣b)=4.
②如图2,连结OB′,OD,分别交AD,B′F于点H,K.记四边形OKGH的面积为S1,△DGK的面积为S2,当a=1时,求的值.
【分析】(1)由四边形ABCD是矩形,可得∠GEF=∠BFE,而四边形ABFE与A′B′FE关于EF所在直线成轴对称,有∠BFE=∠GFE,故∠GEF=∠GFE,GE=GF;
(2)过G作GH⊥BC于H,设DG=x,可知AE=2x,GE=AD﹣AE﹣DG=8﹣3x=GF,根据点O为矩形ABCD的对称中心,可得CF=AE=2x,故FH=CF﹣CH=x,在Rt△GFH中,x2+42=(8﹣3x)2,解得x的值从而可得AE的长为6﹣2;
(3)①过O作OQ⊥AD于Q,连接OA,OD,OG,由点O为矩形ABCD的对称中心,EF过点O,可得O为EF中点,OA=OD,OQAB=2,证明△GOQ∽△OEQ,得,即GQ EQ=OQ2,故GQ EQ=4,即可得(4﹣a)(4﹣b)=4;
②连接B'D,OG,OB,证明B'F=DE,OD=OB=OB',可得△DOG≌△B'OG(SSS),∠ODG=∠OB'G,从而△DGK≌△B'GH(ASA),DK=B'H,GK=GH,即可证△OGK≌△OGH(SSS),得S△OGK=S△OGH,有,而∠EGF=∠DGB',GE=GF,GD=GB',知EF∥B'D,可得△OKF∽△DKB',△EGF∽△DGB',得,,又△EGF∽△DGB',有,当a=1时,b,即AE=1,DG,即可得.
【解答】(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠GEF=∠BFE,
∵四边形ABFE与A′B′FE关于EF所在直线成轴对称,
∴∠BFE=∠GFE,
∴∠GEF=∠GFE,
∴GE=GF;
(2)解:过G作GH⊥BC于H,如图:
设DG=x,则AE=2x,
∴GE=AD﹣AE﹣DG=8﹣3x=GF,
∵∠GHC=∠C=∠D=90°,
∴四边形GHCD是矩形,
∴GH=CD=AB=4,CH=DG=x,
∵点O为矩形ABCD的对称中心,
∴CF=AE=2x,
∴FH=CF﹣CH=x,
在Rt△GFH中,FH2+GH2=GF2,
∴x2+42=(8﹣3x)2,
解得x=3(此时AE大于AD,舍去)或x=3,
∴AE=2x=6﹣2;
∴AE的长为6﹣2;
(3)①证明:过O作OQ⊥AD于Q,连接OA,OD,OG,如图:
∵点O为矩形ABCD的对称中心,EF过点O,
∴O为EF中点,OA=OD,OQAB=2,
∵GE=GF,
∴OG⊥EF,
∴∠GOQ=90°﹣∠EOQ=∠QEO,
∵∠GQO=90°=∠OQE,
∴△GOQ∽△OEQ,
∴,即GQ EQ=OQ2,
∴GQ EQ=4,
∵OA=OD,OQ⊥AD,
∴AQ=DQAD=4,
∴EQ=AQ﹣AE=4﹣a,GQ=DQ﹣GD=4﹣b,
∴(4﹣a)(4﹣b)=4;
②解:连接B'D,OG,OB,如图:
∵四边形ABFE与A′B′FE关于EF所在直线成轴对称,
∴BF=B'F,
∵点O为矩形ABCD的对称中心,
∴BF=DE,
∴B'F=DE,
同理OD=OB=OB',
由(1)知GF=GE,
∴B'F﹣GF=DE﹣GE,即B'G=DG,
∵OG=OG,
∴△DOG≌△B'OG(SSS),
∴∠ODG=∠OB'G,
∵DG=B'G,∠DGK=∠B'GH,
∴△DGK≌△B'GH(ASA),
∴DK=B'H,GK=GH,
∴OD﹣DK=OB'﹣B'H,即OK=OH,
∵OG=OG,
∴△OGK≌△OGH(SSS),
∴S△OGK=S△OGH,
∴S1=2S△OGK,
∴,
∵∠EGF=∠DGB',GE=GF,GD=GB',
∴∠GEF=∠GFE=∠GDB'=∠GB'D,
∴EF∥B'D,
∴△OKF∽△DKB',△EGF∽△DGB',
∴,
∵,
∴,
∵△EGF∽△DGB',
∴,
当a=1时,由①知(4﹣1)×(4﹣b)=4,
∴b,
∴AE=1,DG,
∴GE=AD﹣AE﹣DG,
∴,
∴的值为.
21世纪教育网(www.21cnjy.com)
同课章节目录
