第一章三角形的证明单元测试北师大版2024—2025学年八年级下册(含答案)
文档属性
| 名称 | 第一章三角形的证明单元测试北师大版2024—2025学年八年级下册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 518.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-01 15:31:40 | ||
图片预览


文档简介
第一章三角形的证明单元测试北师大版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.下列各组数中不能作为直角三角形的三边长的是( )
A.6,8,10 B.7,24,25 C.1.5,2,3 D.9,12,15
2.下列条件不能判断△ABC是等边三角形的是( )
A.∠A=∠B=∠C B.AB=BC,AC=BC
C.AB=BC,∠B=60° D.AB=BC,∠A=∠C
3.若等腰三角形的一边长为3cm,周长为15cm,则此等腰三角形的底边长是( )
A.3cm或9cm B.9cm C.3cm D.3cm或6cm
4.如图,∠A=36°,∠DBC=36°,∠C=72°,则图中等腰三角形有( )
A.0个 B.1个 C.2个 D.3个
5.如图,在△ABC中,DE,FG分别是线段AB,BC的垂直平分线,若∠ABC=100°,则∠DBF的度数是( )
A.20° B.30° C.40° D.50°
6.如图,OP平分∠AOB,PC⊥OA于点C,点D在OB上,若PC=3,OD=6,则△POD的面积为( )
A.3 B.6 C.9 D.18
7.如果直角三角形的两条边长分别是3和4,则第三边的长是( )
A.7 B.5 C. D.5或
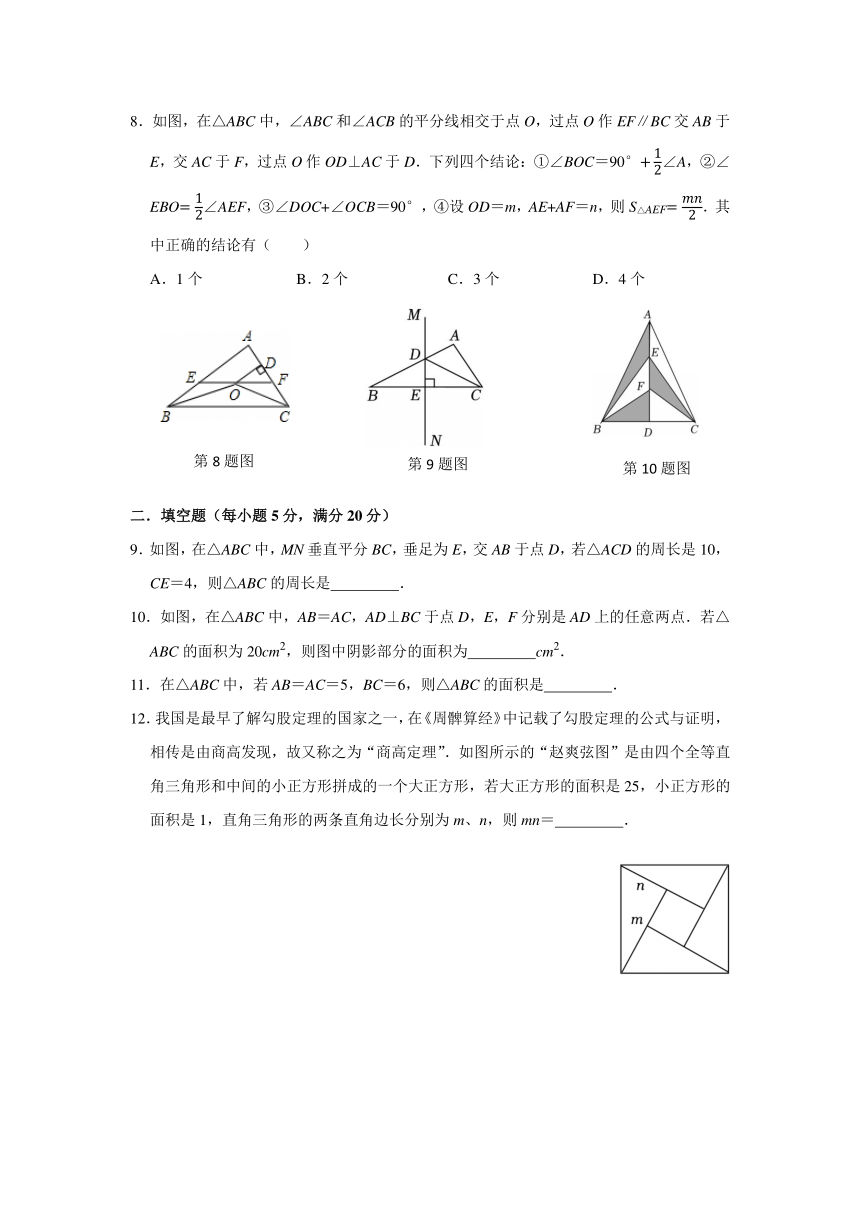
8.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:①∠BOC=90°∠A,②∠EBO∠AEF,③∠DOC+∠OCB=90°,④设OD=m,AE+AF=n,则S△AEF.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(每小题5分,满分20分)
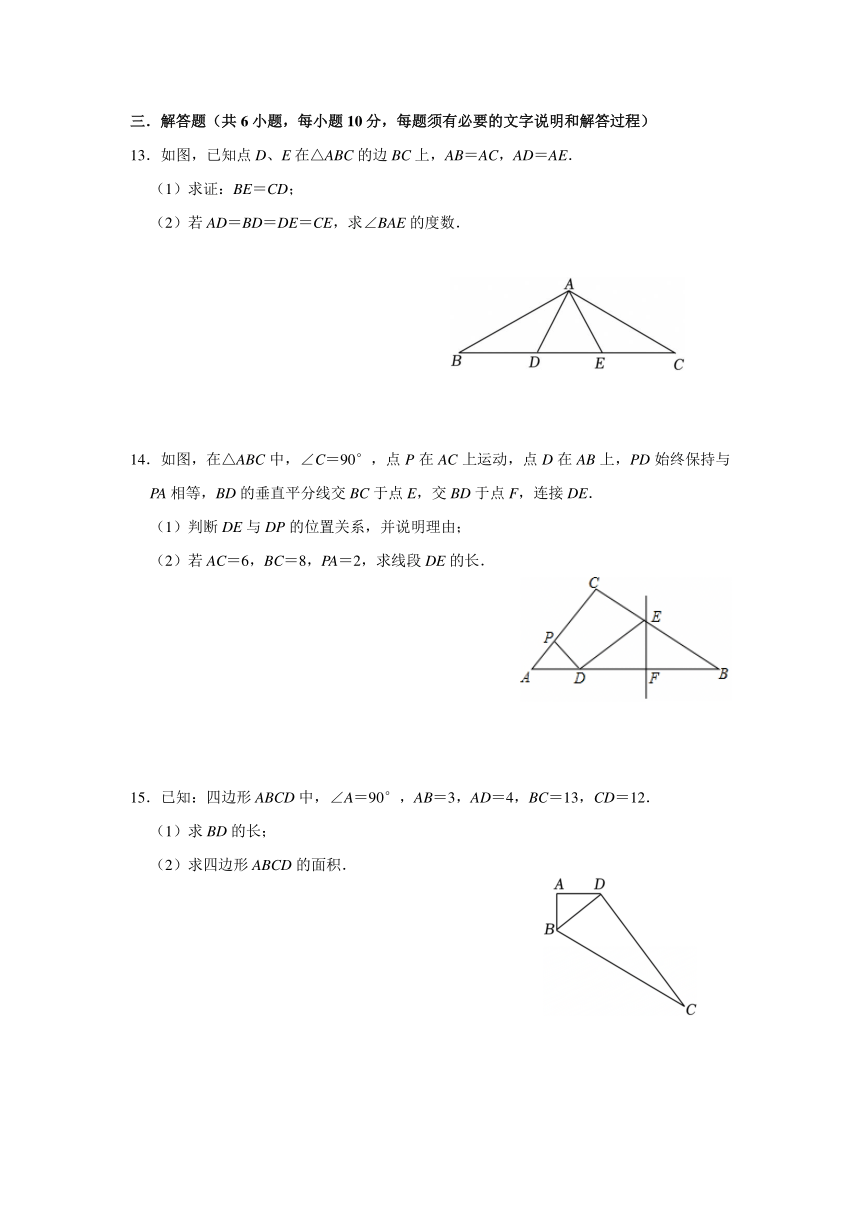
9.如图,在△ABC中,MN垂直平分BC,垂足为E,交AB于点D,若△ACD的周长是10,CE=4,则△ABC的周长是 .
10.如图,在△ABC中,AB=AC,AD⊥BC于点D,E,F分别是AD上的任意两点.若△ABC的面积为20cm2,则图中阴影部分的面积为 cm2.
11.在△ABC中,若AB=AC=5,BC=6,则△ABC的面积是 .
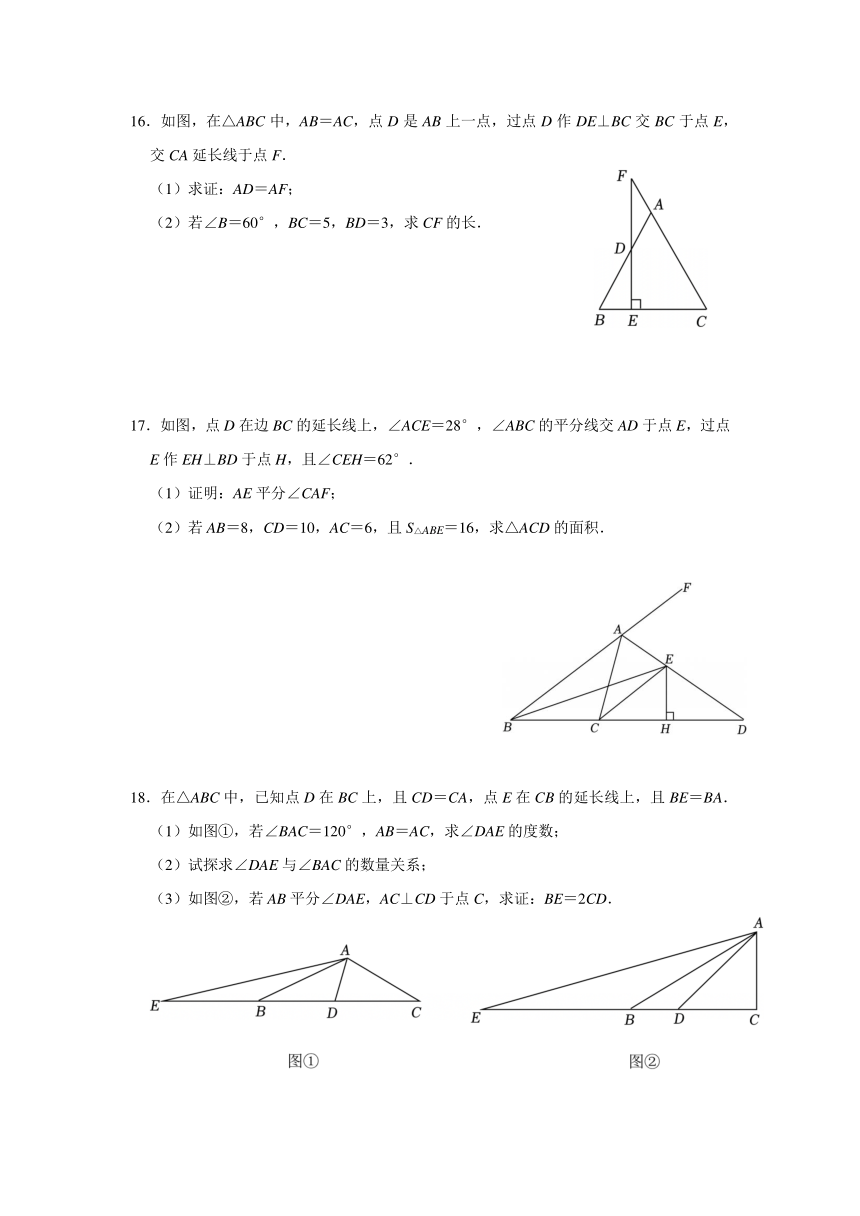
12.我国是最早了解勾股定理的国家之一,在《周髀算经》中记载了勾股定理的公式与证明,相传是由商高发现,故又称之为“商高定理”.如图所示的“赵爽弦图”是由四个全等直角三角形和中间的小正方形拼成的一个大正方形,若大正方形的面积是25,小正方形的面积是1,直角三角形的两条直角边长分别为m、n,则mn= .
三.解答题(共6小题,每小题10分,每题须有必要的文字说明和解答过程)
13.如图,已知点D、E在△ABC的边BC上,AB=AC,AD=AE.
(1)求证:BE=CD;
(2)若AD=BD=DE=CE,求∠BAE的度数.
14.如图,在△ABC中,∠C=90°,点P在AC上运动,点D在AB上,PD始终保持与PA相等,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)判断DE与DP的位置关系,并说明理由;
(2)若AC=6,BC=8,PA=2,求线段DE的长.
15.已知:四边形ABCD中,∠A=90°,AB=3,AD=4,BC=13,CD=12.
(1)求BD的长;
(2)求四边形ABCD的面积.
16.如图,在△ABC中,AB=AC,点D是AB上一点,过点D作DE⊥BC交BC于点E,交CA延长线于点F.
(1)求证:AD=AF;
(2)若∠B=60°,BC=5,BD=3,求CF的长.
17.如图,点D在边BC的延长线上,∠ACE=28°,∠ABC的平分线交AD于点E,过点E作EH⊥BD于点H,且∠CEH=62°.
(1)证明:AE平分∠CAF;
(2)若AB=8,CD=10,AC=6,且S△ABE=16,求△ACD的面积.
18.在△ABC中,已知点D在BC上,且CD=CA,点E在CB的延长线上,且BE=BA.
(1)如图①,若∠BAC=120°,AB=AC,求∠DAE的度数;
(2)试探求∠DAE与∠BAC的数量关系;
(3)如图②,若AB平分∠DAE,AC⊥CD于点C,求证:BE=2CD.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8
答案 C D C D A C D D
二、填空题
9.【解答】解:∵MN垂直平分BC,CE=4,
∴DB=DC,BC=2CE=8,
∵△ACD的周长是10,
∴AC+AD+DC=10,
∴AC+AD+DB=AC+AB=10,
∴△ABC的周长=AC+AB+BC=10+8=18,
故答案为:18.
10.【解答】解:∵在△ABC中,AB=AC,AD⊥BC于点D,
∴BD=CD,
∴S△BEF=S△CEF,
∵,
∴阴影部分面积为,
故答案为:10.
11.【解答】解:取BC的中点D,连接AD,
∵AB=AC=5,
∴AD⊥BC,BD=3,
∴AD4,
∴△ABC的面积6×4=12,
故答案为:12.
12.【解答】解:根据题意,大正方形的面积是25,
∴根据勾股定理可得,m2+n2=25,
∵小正方形的面积是1,即(m﹣n)2=1,
∴m2﹣2mn+n2=1,
∴25﹣2mn=1,
∴2mn=24,
解得mn=12,
所以mn的长为12,
故答案为:12.
三、解答题
13.【解答】(1)证明:如图,过点A作AF⊥BC于F,
由条件可知BF=CF,
∵AD=AE,AF⊥BC,
∴DF=EF,
∴BF+EF=CF+DF,
即BE=CD;
(2)解:由条件可知△ADE是等边三角形,
∴∠DAE=∠ADE=60°,
∵AD=BD,
∴∠DAB=∠DBA,
又∠DAB+∠DBA=∠ADE=60°,
∴,
∴∠BAE=∠BAD+∠DAE=30°+60°=90°.
14.【解答】解:(1)DE⊥DP,
理由如下:∵PD=PA,
∴∠A=∠PDA,
∵EF是BD的垂直平分线,
∴EB=ED,
∴∠B=∠EDB,
∵∠C=90°,
∴∠A+∠B=90°,
∴∠PDA+∠EDB=90°,
∴∠PDE=180°﹣90°=90°,
∴DE⊥DP;
(2)连接PE,设DE=x,则EB=ED=x,CE=8﹣x,
∵∠C=∠PDE=90°,
∴PC2+CE2=PE2=PD2+DE2,
∴42+(8﹣x)2=22+x2,
解得:x=4.75,
则DE=4.75.
15.【解答】解:(1)在△ABD中,∠A=90°,AB=3,DA=4,
根据勾股定理得,BD5;
(2)在△BCD中,BC=13,CD=12,BD=5,
∴CD2+BD2=122+52=132=BC2,
∴△BCD为直角三角形,且∠BDC=90°,
∴S四边形ABCD=S△ABD+S△BCD
AB ADCD BD
3×412×5
=36.
16.【解答】(1)证明:∵AB=AC,
∴∠B=∠C,
∵DE⊥BC,
∴∠BDE+∠B=90°,∠F+∠C=90°,
∴∠F=∠BDE,
∵∠BDE=∠FDA,
∴∠F=∠FDA,
∴AF=AD;
(2)解:∵∠B=60°,DE⊥BC,
∴∠BDE=30°,
∵BD=3,
∴,
∴,
∵∠B=60°,AB=AC,
∴△ABC是等边三角形,
∴∠C=60°,
∵DE⊥BC,
∴∠F=90﹣∠C=90°﹣60°=30°,
∴CF=2CE=27.
17.【解答】(1)证明:过E点作EM⊥BF于M,EN⊥AC与N,
∵BE平分∠ABC,
∴EM=EH,
∵∠ACE=28°,∠CEH=62°,
∴∠HCE=90°﹣∠CEH=90°﹣62°=28°=∠ACE,
∴EN=EH,
∴EM=EN,
∴AE平分∠CAF;
(2)∵AB=8,CD=10,AC=6,且S△ABE=16,
∴,
∴EM=4,
∴EN=EH=EM=4,
∴S△ACD=S△ACE+S△CED
=32,
∴△ACD的面积为32.
18.【解答】(1)解:∵∠BAC=120°,AB=AC,
∴∠C=∠ABC(180°﹣∠BAC)=30°,
∵CD=CA,
∴∠CAD=∠CDA(180°﹣∠C)=75°,
∴∠BAD=∠BAC﹣∠CAD=45°,
∵BE=BA,
∴∠E=∠BAE,
∵∠ABC=∠E+∠BAE=2∠BAE,
∴2∠BAE=30°,
∴∠BAE=15°,
∴∠DAE=∠BAE+∠BAD=15°+45°=60°;
(2)解:∠DAE与∠BAC的数量关系是:∠BAC=2∠DAE,理由如下:
∵CD=CA,
∴设∠CAD=∠CDA=α,
∵BE=BA,
设∠E=∠BAE=β,
∴∠ABD=∠E+∠BAE=2β,
∵∠CDA=∠ABD+∠DAB,
∴∠DAB=∠CDA﹣∠ABD=α﹣2β,
∴∠BAC=∠DAB+∠CAD=α﹣2β+α=2(α﹣β),
又∵∠DAE=∠BAE+∠DAB=β+α﹣2β=α﹣β,
∴∠BAC=2∠DAE;
(3)证明:∵AB平分∠DAE,
∴设∠BAE=∠BAD=θ,
∵BE=BA,
∴∠E=∠BAE=θ,
∴∠ABD=∠E+∠BAE=2θ,
∵CD=CA,AC⊥CD,
∴△CAD是等腰直角三角形,
∴∠ACD=45°,
又∵∠ACD=∠ABD+∠BAD=3θ,
∴3θ=45°,
∴θ=15°,
∴∠ABD=2θ=30°,
在Rt△ABC中,∠ABD=30°,
∴BA=2CA,
∵CD=CA,BE=BA,
∴BE=2CD.
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.下列各组数中不能作为直角三角形的三边长的是( )
A.6,8,10 B.7,24,25 C.1.5,2,3 D.9,12,15
2.下列条件不能判断△ABC是等边三角形的是( )
A.∠A=∠B=∠C B.AB=BC,AC=BC
C.AB=BC,∠B=60° D.AB=BC,∠A=∠C
3.若等腰三角形的一边长为3cm,周长为15cm,则此等腰三角形的底边长是( )
A.3cm或9cm B.9cm C.3cm D.3cm或6cm
4.如图,∠A=36°,∠DBC=36°,∠C=72°,则图中等腰三角形有( )
A.0个 B.1个 C.2个 D.3个
5.如图,在△ABC中,DE,FG分别是线段AB,BC的垂直平分线,若∠ABC=100°,则∠DBF的度数是( )
A.20° B.30° C.40° D.50°
6.如图,OP平分∠AOB,PC⊥OA于点C,点D在OB上,若PC=3,OD=6,则△POD的面积为( )
A.3 B.6 C.9 D.18
7.如果直角三角形的两条边长分别是3和4,则第三边的长是( )
A.7 B.5 C. D.5或
8.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:①∠BOC=90°∠A,②∠EBO∠AEF,③∠DOC+∠OCB=90°,④设OD=m,AE+AF=n,则S△AEF.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(每小题5分,满分20分)
9.如图,在△ABC中,MN垂直平分BC,垂足为E,交AB于点D,若△ACD的周长是10,CE=4,则△ABC的周长是 .
10.如图,在△ABC中,AB=AC,AD⊥BC于点D,E,F分别是AD上的任意两点.若△ABC的面积为20cm2,则图中阴影部分的面积为 cm2.
11.在△ABC中,若AB=AC=5,BC=6,则△ABC的面积是 .
12.我国是最早了解勾股定理的国家之一,在《周髀算经》中记载了勾股定理的公式与证明,相传是由商高发现,故又称之为“商高定理”.如图所示的“赵爽弦图”是由四个全等直角三角形和中间的小正方形拼成的一个大正方形,若大正方形的面积是25,小正方形的面积是1,直角三角形的两条直角边长分别为m、n,则mn= .
三.解答题(共6小题,每小题10分,每题须有必要的文字说明和解答过程)
13.如图,已知点D、E在△ABC的边BC上,AB=AC,AD=AE.
(1)求证:BE=CD;
(2)若AD=BD=DE=CE,求∠BAE的度数.
14.如图,在△ABC中,∠C=90°,点P在AC上运动,点D在AB上,PD始终保持与PA相等,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)判断DE与DP的位置关系,并说明理由;
(2)若AC=6,BC=8,PA=2,求线段DE的长.
15.已知:四边形ABCD中,∠A=90°,AB=3,AD=4,BC=13,CD=12.
(1)求BD的长;
(2)求四边形ABCD的面积.
16.如图,在△ABC中,AB=AC,点D是AB上一点,过点D作DE⊥BC交BC于点E,交CA延长线于点F.
(1)求证:AD=AF;
(2)若∠B=60°,BC=5,BD=3,求CF的长.
17.如图,点D在边BC的延长线上,∠ACE=28°,∠ABC的平分线交AD于点E,过点E作EH⊥BD于点H,且∠CEH=62°.
(1)证明:AE平分∠CAF;
(2)若AB=8,CD=10,AC=6,且S△ABE=16,求△ACD的面积.
18.在△ABC中,已知点D在BC上,且CD=CA,点E在CB的延长线上,且BE=BA.
(1)如图①,若∠BAC=120°,AB=AC,求∠DAE的度数;
(2)试探求∠DAE与∠BAC的数量关系;
(3)如图②,若AB平分∠DAE,AC⊥CD于点C,求证:BE=2CD.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8
答案 C D C D A C D D
二、填空题
9.【解答】解:∵MN垂直平分BC,CE=4,
∴DB=DC,BC=2CE=8,
∵△ACD的周长是10,
∴AC+AD+DC=10,
∴AC+AD+DB=AC+AB=10,
∴△ABC的周长=AC+AB+BC=10+8=18,
故答案为:18.
10.【解答】解:∵在△ABC中,AB=AC,AD⊥BC于点D,
∴BD=CD,
∴S△BEF=S△CEF,
∵,
∴阴影部分面积为,
故答案为:10.
11.【解答】解:取BC的中点D,连接AD,
∵AB=AC=5,
∴AD⊥BC,BD=3,
∴AD4,
∴△ABC的面积6×4=12,
故答案为:12.
12.【解答】解:根据题意,大正方形的面积是25,
∴根据勾股定理可得,m2+n2=25,
∵小正方形的面积是1,即(m﹣n)2=1,
∴m2﹣2mn+n2=1,
∴25﹣2mn=1,
∴2mn=24,
解得mn=12,
所以mn的长为12,
故答案为:12.
三、解答题
13.【解答】(1)证明:如图,过点A作AF⊥BC于F,
由条件可知BF=CF,
∵AD=AE,AF⊥BC,
∴DF=EF,
∴BF+EF=CF+DF,
即BE=CD;
(2)解:由条件可知△ADE是等边三角形,
∴∠DAE=∠ADE=60°,
∵AD=BD,
∴∠DAB=∠DBA,
又∠DAB+∠DBA=∠ADE=60°,
∴,
∴∠BAE=∠BAD+∠DAE=30°+60°=90°.
14.【解答】解:(1)DE⊥DP,
理由如下:∵PD=PA,
∴∠A=∠PDA,
∵EF是BD的垂直平分线,
∴EB=ED,
∴∠B=∠EDB,
∵∠C=90°,
∴∠A+∠B=90°,
∴∠PDA+∠EDB=90°,
∴∠PDE=180°﹣90°=90°,
∴DE⊥DP;
(2)连接PE,设DE=x,则EB=ED=x,CE=8﹣x,
∵∠C=∠PDE=90°,
∴PC2+CE2=PE2=PD2+DE2,
∴42+(8﹣x)2=22+x2,
解得:x=4.75,
则DE=4.75.
15.【解答】解:(1)在△ABD中,∠A=90°,AB=3,DA=4,
根据勾股定理得,BD5;
(2)在△BCD中,BC=13,CD=12,BD=5,
∴CD2+BD2=122+52=132=BC2,
∴△BCD为直角三角形,且∠BDC=90°,
∴S四边形ABCD=S△ABD+S△BCD
AB ADCD BD
3×412×5
=36.
16.【解答】(1)证明:∵AB=AC,
∴∠B=∠C,
∵DE⊥BC,
∴∠BDE+∠B=90°,∠F+∠C=90°,
∴∠F=∠BDE,
∵∠BDE=∠FDA,
∴∠F=∠FDA,
∴AF=AD;
(2)解:∵∠B=60°,DE⊥BC,
∴∠BDE=30°,
∵BD=3,
∴,
∴,
∵∠B=60°,AB=AC,
∴△ABC是等边三角形,
∴∠C=60°,
∵DE⊥BC,
∴∠F=90﹣∠C=90°﹣60°=30°,
∴CF=2CE=27.
17.【解答】(1)证明:过E点作EM⊥BF于M,EN⊥AC与N,
∵BE平分∠ABC,
∴EM=EH,
∵∠ACE=28°,∠CEH=62°,
∴∠HCE=90°﹣∠CEH=90°﹣62°=28°=∠ACE,
∴EN=EH,
∴EM=EN,
∴AE平分∠CAF;
(2)∵AB=8,CD=10,AC=6,且S△ABE=16,
∴,
∴EM=4,
∴EN=EH=EM=4,
∴S△ACD=S△ACE+S△CED
=32,
∴△ACD的面积为32.
18.【解答】(1)解:∵∠BAC=120°,AB=AC,
∴∠C=∠ABC(180°﹣∠BAC)=30°,
∵CD=CA,
∴∠CAD=∠CDA(180°﹣∠C)=75°,
∴∠BAD=∠BAC﹣∠CAD=45°,
∵BE=BA,
∴∠E=∠BAE,
∵∠ABC=∠E+∠BAE=2∠BAE,
∴2∠BAE=30°,
∴∠BAE=15°,
∴∠DAE=∠BAE+∠BAD=15°+45°=60°;
(2)解:∠DAE与∠BAC的数量关系是:∠BAC=2∠DAE,理由如下:
∵CD=CA,
∴设∠CAD=∠CDA=α,
∵BE=BA,
设∠E=∠BAE=β,
∴∠ABD=∠E+∠BAE=2β,
∵∠CDA=∠ABD+∠DAB,
∴∠DAB=∠CDA﹣∠ABD=α﹣2β,
∴∠BAC=∠DAB+∠CAD=α﹣2β+α=2(α﹣β),
又∵∠DAE=∠BAE+∠DAB=β+α﹣2β=α﹣β,
∴∠BAC=2∠DAE;
(3)证明:∵AB平分∠DAE,
∴设∠BAE=∠BAD=θ,
∵BE=BA,
∴∠E=∠BAE=θ,
∴∠ABD=∠E+∠BAE=2θ,
∵CD=CA,AC⊥CD,
∴△CAD是等腰直角三角形,
∴∠ACD=45°,
又∵∠ACD=∠ABD+∠BAD=3θ,
∴3θ=45°,
∴θ=15°,
∴∠ABD=2θ=30°,
在Rt△ABC中,∠ABD=30°,
∴BA=2CA,
∵CD=CA,BE=BA,
∴BE=2CD.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
