期中评估检测题(无答案)2024-2025学年北师大版七年级下册数学
文档属性
| 名称 | 期中评估检测题(无答案)2024-2025学年北师大版七年级下册数学 |  | |
| 格式 | docx | ||
| 文件大小 | 76.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-02 10:55:52 | ||
图片预览

文档简介
期中评估检测题
( 时间:120 分钟 总分:120 分)
1 . 选择题( 每题 3 分,共 30 分)
(1) 计算 a 2 ·a 3 的结果等于( ) .
A. a 5 B. a 9 C. a 6 D. a - 1
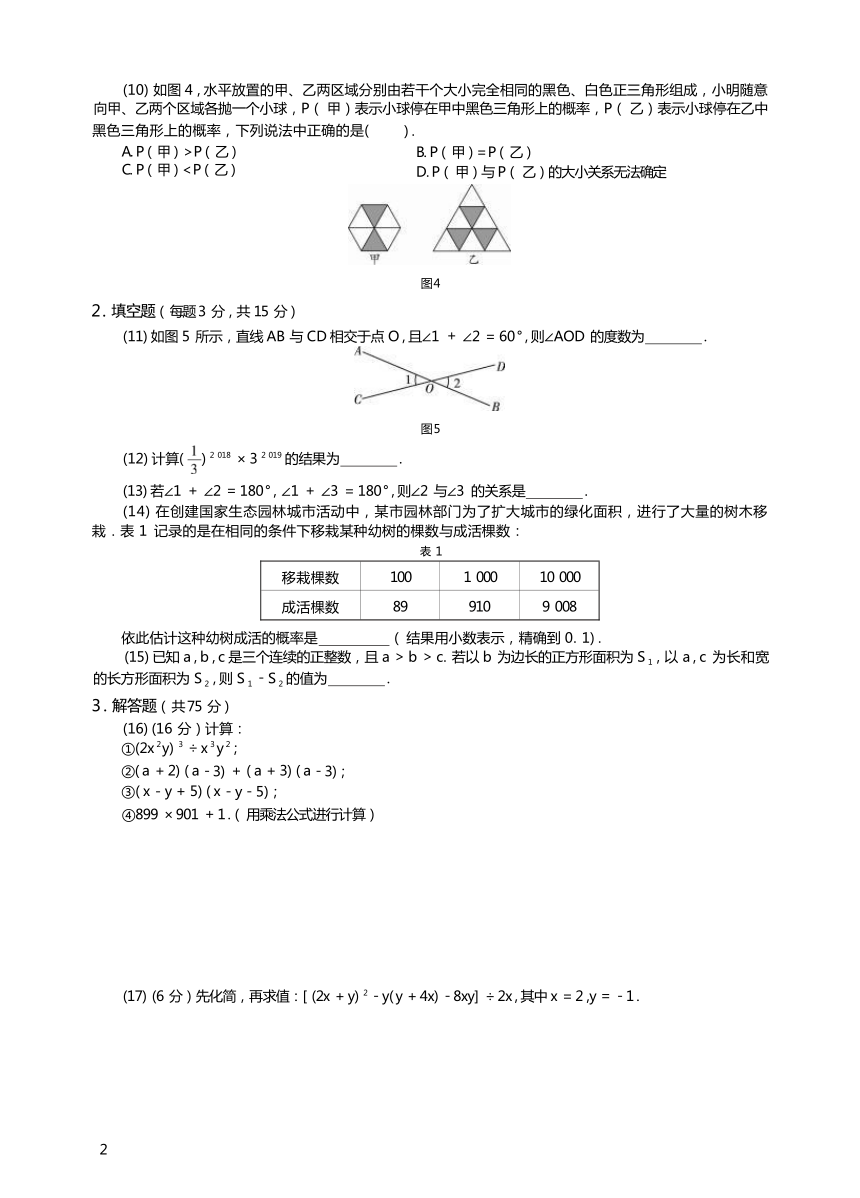
(2) 如图 1 , 点 O 是∠ABE 的边 BA 上的一点,过点 O 的直线 CD∥BE. 若∠AOC = 40 ° , 则 ∠B 的度数为 ( ) .
A. 160 ° B. 140 ° C. 60 ° D. 50 °
(3) 下列计算正确的是( ) .
A. a 3 + a 2 = a 5 B. ( - a 3 b 2 ) 2 = a 6 b 4
C. 2x 2 ÷ 2x 2 = 0 D. - 3 = 8
(4) 用 3D 打印技术打印出的高精密游标卡尺,其误差只有 ± 0. 000 063 米,将 0. 000 063 用科学记数法 表示为( ) .
A. 6. 3 × 10 5 B. 6. 3 × 10 - 6
C. 6. 3 × 10 - 5 D. 0. 63 × 10 5
(5) 已知点 C 在∠AOB 的边 OB 上,用尺规过点 C 作 CN∥OA , 作图痕迹如图 2 所示.下列对弧 FG 的描 述,正确的是( ) .
A. 以点 C 为圆心,OD 的长为半径的弧 B. 以点 C 为圆心,OM 的长为半径的弧 C. 以点E 为圆心,DM 的长为半径的弧 D. 以点E 为圆心,CE 的长为半径的弧
图 1 图 2
(6) 下列各式能用平方差公式运算的是( ) .
(
A.
(
x
+ a)
(
x
+ a)
B.
( a
+ x)
( a
- b)
)C. ( - x - b) ( x + b) D. ( - a + b) ( - a - b)
(7) 从 n 个苹果和 3 个雪梨中任选 1 个,若选中苹果的概率是,则 n 的值是( ) .
A. 6 B. 3 C. 2 D. 1
(8) 下列各式,计算结果为 3 - 2 的是( ) .
(
(9) 如图 3 ,
点 F
,
E 分别在线段
AB
和 CD 上,下列条件能判定
AB∥CD
的是( ) .
)A. 3 4 ÷ 3 6 B. 3 6 ÷ 3 4 C. 3 3 ÷ 3 6 D. ( - 3) × ( - 3)
图3
A. ∠1 = ∠2 B. ∠1 = ∠4
C. ∠4 = ∠2 D. ∠3 = ∠4
1
(10) 如图 4 , 水平放置的甲、乙两区域分别由若干个大小完全相同的黑色、白色正三角形组成,小明随意 向甲、乙两个区域各抛一个小球,P( 甲)表示小球停在甲中黑色三角形上的概率,P( 乙)表示小球停在乙中
2
黑色三角形上的概率,下列说法中正确的是(
A. P( 甲)>P( 乙) C. P( 甲)< P( 乙)
) .
B. P( 甲)= P( 乙)
D. P( 甲)与 P( 乙)的大小关系无法确定
图4
2 . 填空题( 每题 3 分,共 15 分)
(11) 如图 5 所示,直线 AB 与 CD 相交于点 O , 且∠1 + ∠2 = 60 ° , 则∠AOD 的度数为 .
图5
(12) 计算( ) 2 018 × 3 2 019 的结果为 .
(13) 若∠1 + ∠2 = 180 ° , ∠1 + ∠3 = 180 ° , 则∠2 与∠3 的关系是 .
(14) 在创建国家生态园林城市活动中,某市园林部门为了扩大城市的绿化面积,进行了大量的树木移 栽.表 1 记录的是在相同的条件下移栽某种幼树的棵数与成活棵数:
表 1
移栽棵数 100 1 000 10 000
成活棵数 89 910 9 008
依此估计这种幼树成活的概率是 ( 结果用小数表示,精确到 0. 1) .
(15) 已知 a , b , c 是三个连续的正整数,且 a > b > c. 若以 b 为边长的正方形面积为 S 1 , 以 a , c 为长和宽
的长方形面积为 S 2 , 则 S 1 - S 2 的值为 .
3 . 解答题( 共 75 分)
(16) (16 分)计算:
①(2x 2 y) 3 ÷ x 3 y 2 ;
(
③(
x
- y + 5) (
x
-
y
-
5)
;
)②( a + 2) ( a - 3) + ( a + 3) ( a - 3) ;
(
④899
×
901
+
1
.( 用乘法公式进行计算)
)
(17) (6 分)先化简,再求值:[ (2x + y) 2 - y( y + 4x) - 8xy] ÷ 2x , 其中 x = 2 ,y = - 1 .
(18) (6 分)已知:∠α , ∠β. 求作:∠AOB , 使得∠AOB = ∠α + ∠β.( 要求:用尺规作图,不写作法,保留
作图痕迹)
图6
(19) (8 分)如图 7 , 已知直线 AB∥CD , 直线 EF 分别与 AB , CD 相交于点 O , M , 射线 OP 在∠AOE 的内 部,且 OP⊥EF , 垂足为 O. 若∠AOP = 30 ° , 求∠EMD 的度数 .
图7
(20) (8 分)某批足球的质量检测结果如表 2 所示:
表2
抽取足球数 n 100 200 400 600 800 1 000
合格的数量 m 93 192 384 564 759 950
合格的频率 0. 93 0. 96 0. 96 0. 94
图8
①填写表中的空格( 结果保留 0. 01) ;
②画出合格的频率的折线统计图;
③从这批足球中任意抽取一个足球是合格品的概率估计值是多少?并说明理由;
④若某工厂计划生产 10 000 个足球,试估计生产出的足球中合格的数量有 个.
(21) (10 分)如图 9 , 某校有一块长为(3a + b) m , 宽为(2a + b) m 的长方形空地,中间是边长为( a + b) m 的正方形草坪,其余为活动场地,学校计划将活动场地( 阴影部分)进行硬化 .
①用含 a , b 的代数式表示需要硬化的面积并化简;
3
②当 a = 5 , b = 2 时,求需要硬化的面积.
图9
(22)(10 分)学习整式的乘法时可以发现:用两种不同的方法表示同一个图形的面积可以得到一个等 式,进而可以利用得到的等式解决问题.
图 10 图 11
①如图 10 , 是由边长分别为 a , b 的正方形和长为 a、宽为 b 的长方形拼成的大长方形,由图 10 可得等 式:(a + 2b)(a + b) = ;
②A. 如图 11 , 是由几个小正方形和小长方形拼成的一个边长为( a + b + c) 的大正方形,用不同的方法 表示这个大正方形的面积,得到的等式为 ;
B. 已知 a + b + c = 11 , ab + bc + ac = 38 , 利用题 A 中所得等式,求代数式 a 2 + b 2 + c 2 的值 .
(23)( 11 分)下图是明明设计的智力拼图玩具的一部分,现在明明遇到了两个问题,请你帮助解决:
①如图 12 , ∠D = 32 ° , ∠ACD = 60 ° , 为保证 AB∥DE , 则∠A 等于多少度?
②如图 13 , ∠G , ∠GFH , ∠H 之间有什么样的关系时,GP∥HQ
4
( 时间:120 分钟 总分:120 分)
1 . 选择题( 每题 3 分,共 30 分)
(1) 计算 a 2 ·a 3 的结果等于( ) .
A. a 5 B. a 9 C. a 6 D. a - 1
(2) 如图 1 , 点 O 是∠ABE 的边 BA 上的一点,过点 O 的直线 CD∥BE. 若∠AOC = 40 ° , 则 ∠B 的度数为 ( ) .
A. 160 ° B. 140 ° C. 60 ° D. 50 °
(3) 下列计算正确的是( ) .
A. a 3 + a 2 = a 5 B. ( - a 3 b 2 ) 2 = a 6 b 4
C. 2x 2 ÷ 2x 2 = 0 D. - 3 = 8
(4) 用 3D 打印技术打印出的高精密游标卡尺,其误差只有 ± 0. 000 063 米,将 0. 000 063 用科学记数法 表示为( ) .
A. 6. 3 × 10 5 B. 6. 3 × 10 - 6
C. 6. 3 × 10 - 5 D. 0. 63 × 10 5
(5) 已知点 C 在∠AOB 的边 OB 上,用尺规过点 C 作 CN∥OA , 作图痕迹如图 2 所示.下列对弧 FG 的描 述,正确的是( ) .
A. 以点 C 为圆心,OD 的长为半径的弧 B. 以点 C 为圆心,OM 的长为半径的弧 C. 以点E 为圆心,DM 的长为半径的弧 D. 以点E 为圆心,CE 的长为半径的弧
图 1 图 2
(6) 下列各式能用平方差公式运算的是( ) .
(
A.
(
x
+ a)
(
x
+ a)
B.
( a
+ x)
( a
- b)
)C. ( - x - b) ( x + b) D. ( - a + b) ( - a - b)
(7) 从 n 个苹果和 3 个雪梨中任选 1 个,若选中苹果的概率是,则 n 的值是( ) .
A. 6 B. 3 C. 2 D. 1
(8) 下列各式,计算结果为 3 - 2 的是( ) .
(
(9) 如图 3 ,
点 F
,
E 分别在线段
AB
和 CD 上,下列条件能判定
AB∥CD
的是( ) .
)A. 3 4 ÷ 3 6 B. 3 6 ÷ 3 4 C. 3 3 ÷ 3 6 D. ( - 3) × ( - 3)
图3
A. ∠1 = ∠2 B. ∠1 = ∠4
C. ∠4 = ∠2 D. ∠3 = ∠4
1
(10) 如图 4 , 水平放置的甲、乙两区域分别由若干个大小完全相同的黑色、白色正三角形组成,小明随意 向甲、乙两个区域各抛一个小球,P( 甲)表示小球停在甲中黑色三角形上的概率,P( 乙)表示小球停在乙中
2
黑色三角形上的概率,下列说法中正确的是(
A. P( 甲)>P( 乙) C. P( 甲)< P( 乙)
) .
B. P( 甲)= P( 乙)
D. P( 甲)与 P( 乙)的大小关系无法确定
图4
2 . 填空题( 每题 3 分,共 15 分)
(11) 如图 5 所示,直线 AB 与 CD 相交于点 O , 且∠1 + ∠2 = 60 ° , 则∠AOD 的度数为 .
图5
(12) 计算( ) 2 018 × 3 2 019 的结果为 .
(13) 若∠1 + ∠2 = 180 ° , ∠1 + ∠3 = 180 ° , 则∠2 与∠3 的关系是 .
(14) 在创建国家生态园林城市活动中,某市园林部门为了扩大城市的绿化面积,进行了大量的树木移 栽.表 1 记录的是在相同的条件下移栽某种幼树的棵数与成活棵数:
表 1
移栽棵数 100 1 000 10 000
成活棵数 89 910 9 008
依此估计这种幼树成活的概率是 ( 结果用小数表示,精确到 0. 1) .
(15) 已知 a , b , c 是三个连续的正整数,且 a > b > c. 若以 b 为边长的正方形面积为 S 1 , 以 a , c 为长和宽
的长方形面积为 S 2 , 则 S 1 - S 2 的值为 .
3 . 解答题( 共 75 分)
(16) (16 分)计算:
①(2x 2 y) 3 ÷ x 3 y 2 ;
(
③(
x
- y + 5) (
x
-
y
-
5)
;
)②( a + 2) ( a - 3) + ( a + 3) ( a - 3) ;
(
④899
×
901
+
1
.( 用乘法公式进行计算)
)
(17) (6 分)先化简,再求值:[ (2x + y) 2 - y( y + 4x) - 8xy] ÷ 2x , 其中 x = 2 ,y = - 1 .
(18) (6 分)已知:∠α , ∠β. 求作:∠AOB , 使得∠AOB = ∠α + ∠β.( 要求:用尺规作图,不写作法,保留
作图痕迹)
图6
(19) (8 分)如图 7 , 已知直线 AB∥CD , 直线 EF 分别与 AB , CD 相交于点 O , M , 射线 OP 在∠AOE 的内 部,且 OP⊥EF , 垂足为 O. 若∠AOP = 30 ° , 求∠EMD 的度数 .
图7
(20) (8 分)某批足球的质量检测结果如表 2 所示:
表2
抽取足球数 n 100 200 400 600 800 1 000
合格的数量 m 93 192 384 564 759 950
合格的频率 0. 93 0. 96 0. 96 0. 94
图8
①填写表中的空格( 结果保留 0. 01) ;
②画出合格的频率的折线统计图;
③从这批足球中任意抽取一个足球是合格品的概率估计值是多少?并说明理由;
④若某工厂计划生产 10 000 个足球,试估计生产出的足球中合格的数量有 个.
(21) (10 分)如图 9 , 某校有一块长为(3a + b) m , 宽为(2a + b) m 的长方形空地,中间是边长为( a + b) m 的正方形草坪,其余为活动场地,学校计划将活动场地( 阴影部分)进行硬化 .
①用含 a , b 的代数式表示需要硬化的面积并化简;
3
②当 a = 5 , b = 2 时,求需要硬化的面积.
图9
(22)(10 分)学习整式的乘法时可以发现:用两种不同的方法表示同一个图形的面积可以得到一个等 式,进而可以利用得到的等式解决问题.
图 10 图 11
①如图 10 , 是由边长分别为 a , b 的正方形和长为 a、宽为 b 的长方形拼成的大长方形,由图 10 可得等 式:(a + 2b)(a + b) = ;
②A. 如图 11 , 是由几个小正方形和小长方形拼成的一个边长为( a + b + c) 的大正方形,用不同的方法 表示这个大正方形的面积,得到的等式为 ;
B. 已知 a + b + c = 11 , ab + bc + ac = 38 , 利用题 A 中所得等式,求代数式 a 2 + b 2 + c 2 的值 .
(23)( 11 分)下图是明明设计的智力拼图玩具的一部分,现在明明遇到了两个问题,请你帮助解决:
①如图 12 , ∠D = 32 ° , ∠ACD = 60 ° , 为保证 AB∥DE , 则∠A 等于多少度?
②如图 13 , ∠G , ∠GFH , ∠H 之间有什么样的关系时,GP∥HQ
4
同课章节目录
