2025年中考数学一轮复习 4 二次根式 小测验(含详解)
文档属性
| 名称 | 2025年中考数学一轮复习 4 二次根式 小测验(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 878.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-02 16:59:04 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
4 二次根式
分值:50分 时间30分钟
选择题(15分)
1.(2024·云南·中考真题)式子在实数范围内有意义,则的取值范围是( )
A. B. C. D.
2.(2024·重庆·中考真题)估计的值应在( )
A.8和9之间 B.9和10之间 C.10和11之间 D.11和12之间
3.(2024·山东济宁·中考真题)下列运算正确的是( )
A. B.
C. D.
4.(2024·四川德阳·中考真题)将一组数,按以下方式进行排列:
则第八行左起第1个数是( )
A. B. C. D.
5.(2024·四川南充·中考真题)如图,已知线段,按以下步骤作图:①过点B作,使,连接;②以点C为圆心,以长为半径画弧,交于点D;③以点A为圆心,以长为半径画弧,交于点E.若,则m的值为( )
A. B. C. D.
填空题(15分)
6.(2024·河北·模拟预测)若a的倒数是,则的值为 .
7.(2024·吉林·模拟预测)比较大小: 6.(填“>”或“<”)
8.(2024·吉林长春·二模)与最简二次根式是同类二次根式,则m的值为 .
9.(2024·广东·模拟预测)若恒有式子,则实数的取值范围是 .
10.(2024·四川宜宾·中考真题)如图,正方形的边长为1,M、N是边、上的动点.若,则的最小值为 .
简单题(20分)
11.(2024·甘肃·中考真题)计算:.
12. (2024深圳)先化简,再求值: ,其中
13.(2024·广东·模拟预测)【代数推理】代数推理指从一定条件出发,依据代数的定义、公式、运算法则、等式的性质、不等式的性质等证明已知结果或结论.
【发现问题】小明在计算时发现:对于任意两个连续的正整数m、n,它们的乘积 与较大数的和一定为较大数的平方.
(1)举例验证:当 则
(2)推理证明:小明同学做了如下的证明:
设, m、n是连续的正整数,
∴; ∵, ∴.
∴一定是正数n的平方数.
【类比猜想】小红同学提出:任意两个连续正整数的乘积与较小数的差是较小数的平方.
请你举例验证及推理证明;
【深入思考】若 (m, n为两个连续奇数, 求证:p一定是偶数.
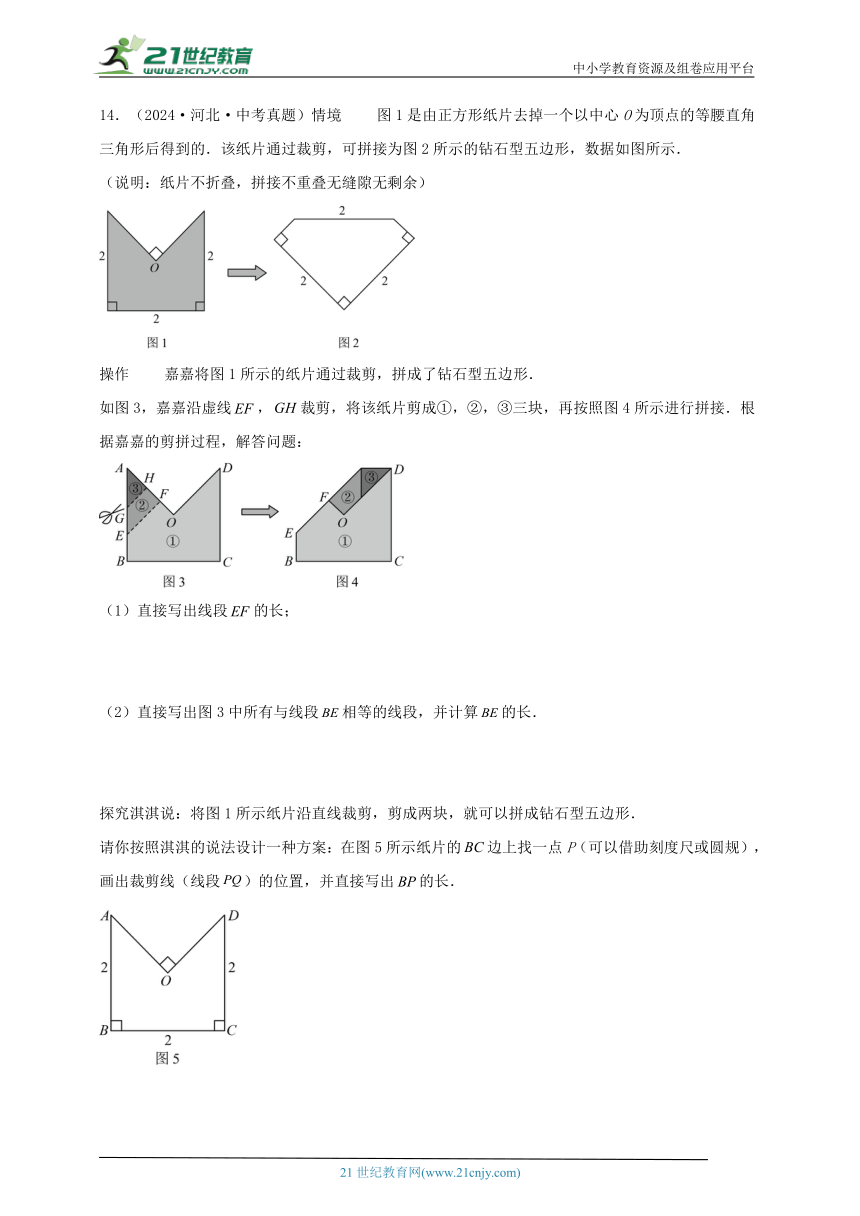
14.(2024·河北·中考真题)情境 图1是由正方形纸片去掉一个以中心O为顶点的等腰直角三角形后得到的.该纸片通过裁剪,可拼接为图2所示的钻石型五边形,数据如图所示.
(说明:纸片不折叠,拼接不重叠无缝隙无剩余)
操作 嘉嘉将图1所示的纸片通过裁剪,拼成了钻石型五边形.
如图3,嘉嘉沿虚线,裁剪,将该纸片剪成①,②,③三块,再按照图4所示进行拼接.根据嘉嘉的剪拼过程,解答问题:
(1)直接写出线段的长;
(2)直接写出图3中所有与线段相等的线段,并计算的长.
探究淇淇说:将图1所示纸片沿直线裁剪,剪成两块,就可以拼成钻石型五边形.
请你按照淇淇的说法设计一种方案:在图5所示纸片的边上找一点P(可以借助刻度尺或圆规),画出裁剪线(线段)的位置,并直接写出的长.
答案:
一、选择题(15分)
1.(2024·云南·中考真题)式子在实数范围内有意义,则的取值范围是( )
A. B. C. D.
【答案】B
【详解】解:∵式子在实数范围内有意义,
∴的取值范围是.
2.(2024·重庆·中考真题)估计的值应在( )
A.8和9之间 B.9和10之间 C.10和11之间 D.11和12之间
【答案】C
【详解】解:∵,
而,
∴,
3.(2024·山东济宁·中考真题)下列运算正确的是( )
A. B.
C. D.
【答案】B
【详解】A. 不能合并,所以A选项错误;
B. ,所以B选项正确;
C. ,所以C选项错误;
D. ,所以D选项错误.
故选:B.
4.(2024·四川德阳·中考真题)将一组数,按以下方式进行排列:
则第八行左起第1个数是( )
A. B. C. D.
【答案】C
【详解】解:由图可知,第一行共有1个数,第二行共有2个数,第三行共有3个数,
归纳类推得:第七行共有个数,
则第八行左起第1个数是,
5.(2024·四川南充·中考真题)如图,已知线段,按以下步骤作图:①过点B作,使,连接;②以点C为圆心,以长为半径画弧,交于点D;③以点A为圆心,以长为半径画弧,交于点E.若,则m的值为( )
A. B. C. D.
【答案】A
【详解】解:∵,
∴,
∵,设
∴,
∴,
由题意得:,
∴,
∵,
∴,
二、填空题(15分)
6.(2024·河北·模拟预测)若a的倒数是,则的值为 .
【答案】
【详解】解:∵a的倒数是,
∴,
∴;
7.(2024·吉林·模拟预测)比较大小: 6.(填“>”或“<”)
【答案】<
【详解】解:,,
,
.
8.(2024·吉林长春·二模)与最简二次根式是同类二次根式,则m的值为 .
【答案】3
【详解】∵与最简二次根式是同类二次根式,
∴,
解得.
9.(2024·广东·模拟预测)若恒有式子,则实数的取值范围是 .
【答案】
【详解】解:,
,
解得:,
故答案为:.
10.(2024·四川宜宾·中考真题)如图,正方形的边长为1,M、N是边、上的动点.若,则的最小值为 .
【答案】/
【详解】解:∵正方形的边长为1,
∴,,
将顺时针旋转得到,则,
∴,,,,
∴点P、B、M、C共线,
∵,
∴,
∵,,,
∴,
∴,
∴,
设,,则,,
∴,
∵,
∴,即,
整理得:,
∴
,
当且仅当,即,也即时,取最小值,
故答案为:.
三、简单题(20分)
11.(2024·甘肃·中考真题)计算:.
【答案】0
【详解】.
12. (2024深圳)先化简,再求值: ,其中
【答案】,
【详解】解:
=
=
=,
当时,原式=.
13.(2024·广东·模拟预测)【代数推理】代数推理指从一定条件出发,依据代数的定义、公式、运算法则、等式的性质、不等式的性质等证明已知结果或结论.
【发现问题】小明在计算时发现:对于任意两个连续的正整数m、n,它们的乘积 与较大数的和一定为较大数的平方.
(1)举例验证:当 则
(2)推理证明:小明同学做了如下的证明:
设, m、n是连续的正整数,
∴; ∵, ∴.
∴一定是正数n的平方数.
【类比猜想】小红同学提出:任意两个连续正整数的乘积与较小数的差是较小数的平方.
请你举例验证及推理证明;
【深入思考】若 (m, n为两个连续奇数, 求证:p一定是偶数.
【详解】解:类比猜想:(1)举例验证:当 则
(2)推理证明:小明同学做了如下的证明:
设, m、n是连续的正整数,
∴;
∵,
∴.
∴一定是正数的平方数.
深入思考:∵m, n为两个连续奇数,,
∴,
∴,
∴,
∴p一定是偶数.
14.(2024·河北·中考真题)情境 图1是由正方形纸片去掉一个以中心O为顶点的等腰直角三角形后得到的.
该纸片通过裁剪,可拼接为图2所示的钻石型五边形,数据如图所示.
(说明:纸片不折叠,拼接不重叠无缝隙无剩余)
操作 嘉嘉将图1所示的纸片通过裁剪,拼成了钻石型五边形.
如图3,嘉嘉沿虚线,裁剪,将该纸片剪成①,②,③三块,再按照图4所示进行拼接.根据嘉嘉的剪拼过程,解答问题:
(1)直接写出线段的长;
(2)直接写出图3中所有与线段相等的线段,并计算的长.
探究淇淇说:将图1所示纸片沿直线裁剪,剪成两块,就可以拼成钻石型五边形.
请你按照淇淇的说法设计一种方案:在图5所示纸片的边上找一点P(可以借助刻度尺或圆规),画出裁剪线(线段)的位置,并直接写出的长.
【答案】(1);(2),;的长为或.
【详解】解:如图,过作于,
结合题意可得:四边形为矩形,
∴,
由拼接可得:,
由正方形的性质可得:,
∴,,为等腰直角三角形,
∴为等腰直角三角形,
设,
∴,
∴,,
∵正方形的边长为,
∴对角线的长,
∴,
∴,
解得:,
∴;
(2)∵为等腰直角三角形,;
∴,
∴,
∵,
,
∴;
如图,以为圆心,为半径画弧交于,交于,则直线为分割线,
此时,,符合要求,
或以圆心,为半径画弧,交于,交于,则直线为分割线,
此时,,
∴,
综上:的长为或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
4 二次根式
分值:50分 时间30分钟
选择题(15分)
1.(2024·云南·中考真题)式子在实数范围内有意义,则的取值范围是( )
A. B. C. D.
2.(2024·重庆·中考真题)估计的值应在( )
A.8和9之间 B.9和10之间 C.10和11之间 D.11和12之间
3.(2024·山东济宁·中考真题)下列运算正确的是( )
A. B.
C. D.
4.(2024·四川德阳·中考真题)将一组数,按以下方式进行排列:
则第八行左起第1个数是( )
A. B. C. D.
5.(2024·四川南充·中考真题)如图,已知线段,按以下步骤作图:①过点B作,使,连接;②以点C为圆心,以长为半径画弧,交于点D;③以点A为圆心,以长为半径画弧,交于点E.若,则m的值为( )
A. B. C. D.
填空题(15分)
6.(2024·河北·模拟预测)若a的倒数是,则的值为 .
7.(2024·吉林·模拟预测)比较大小: 6.(填“>”或“<”)
8.(2024·吉林长春·二模)与最简二次根式是同类二次根式,则m的值为 .
9.(2024·广东·模拟预测)若恒有式子,则实数的取值范围是 .
10.(2024·四川宜宾·中考真题)如图,正方形的边长为1,M、N是边、上的动点.若,则的最小值为 .
简单题(20分)
11.(2024·甘肃·中考真题)计算:.
12. (2024深圳)先化简,再求值: ,其中
13.(2024·广东·模拟预测)【代数推理】代数推理指从一定条件出发,依据代数的定义、公式、运算法则、等式的性质、不等式的性质等证明已知结果或结论.
【发现问题】小明在计算时发现:对于任意两个连续的正整数m、n,它们的乘积 与较大数的和一定为较大数的平方.
(1)举例验证:当 则
(2)推理证明:小明同学做了如下的证明:
设, m、n是连续的正整数,
∴; ∵, ∴.
∴一定是正数n的平方数.
【类比猜想】小红同学提出:任意两个连续正整数的乘积与较小数的差是较小数的平方.
请你举例验证及推理证明;
【深入思考】若 (m, n为两个连续奇数, 求证:p一定是偶数.
14.(2024·河北·中考真题)情境 图1是由正方形纸片去掉一个以中心O为顶点的等腰直角三角形后得到的.该纸片通过裁剪,可拼接为图2所示的钻石型五边形,数据如图所示.
(说明:纸片不折叠,拼接不重叠无缝隙无剩余)
操作 嘉嘉将图1所示的纸片通过裁剪,拼成了钻石型五边形.
如图3,嘉嘉沿虚线,裁剪,将该纸片剪成①,②,③三块,再按照图4所示进行拼接.根据嘉嘉的剪拼过程,解答问题:
(1)直接写出线段的长;
(2)直接写出图3中所有与线段相等的线段,并计算的长.
探究淇淇说:将图1所示纸片沿直线裁剪,剪成两块,就可以拼成钻石型五边形.
请你按照淇淇的说法设计一种方案:在图5所示纸片的边上找一点P(可以借助刻度尺或圆规),画出裁剪线(线段)的位置,并直接写出的长.
答案:
一、选择题(15分)
1.(2024·云南·中考真题)式子在实数范围内有意义,则的取值范围是( )
A. B. C. D.
【答案】B
【详解】解:∵式子在实数范围内有意义,
∴的取值范围是.
2.(2024·重庆·中考真题)估计的值应在( )
A.8和9之间 B.9和10之间 C.10和11之间 D.11和12之间
【答案】C
【详解】解:∵,
而,
∴,
3.(2024·山东济宁·中考真题)下列运算正确的是( )
A. B.
C. D.
【答案】B
【详解】A. 不能合并,所以A选项错误;
B. ,所以B选项正确;
C. ,所以C选项错误;
D. ,所以D选项错误.
故选:B.
4.(2024·四川德阳·中考真题)将一组数,按以下方式进行排列:
则第八行左起第1个数是( )
A. B. C. D.
【答案】C
【详解】解:由图可知,第一行共有1个数,第二行共有2个数,第三行共有3个数,
归纳类推得:第七行共有个数,
则第八行左起第1个数是,
5.(2024·四川南充·中考真题)如图,已知线段,按以下步骤作图:①过点B作,使,连接;②以点C为圆心,以长为半径画弧,交于点D;③以点A为圆心,以长为半径画弧,交于点E.若,则m的值为( )
A. B. C. D.
【答案】A
【详解】解:∵,
∴,
∵,设
∴,
∴,
由题意得:,
∴,
∵,
∴,
二、填空题(15分)
6.(2024·河北·模拟预测)若a的倒数是,则的值为 .
【答案】
【详解】解:∵a的倒数是,
∴,
∴;
7.(2024·吉林·模拟预测)比较大小: 6.(填“>”或“<”)
【答案】<
【详解】解:,,
,
.
8.(2024·吉林长春·二模)与最简二次根式是同类二次根式,则m的值为 .
【答案】3
【详解】∵与最简二次根式是同类二次根式,
∴,
解得.
9.(2024·广东·模拟预测)若恒有式子,则实数的取值范围是 .
【答案】
【详解】解:,
,
解得:,
故答案为:.
10.(2024·四川宜宾·中考真题)如图,正方形的边长为1,M、N是边、上的动点.若,则的最小值为 .
【答案】/
【详解】解:∵正方形的边长为1,
∴,,
将顺时针旋转得到,则,
∴,,,,
∴点P、B、M、C共线,
∵,
∴,
∵,,,
∴,
∴,
∴,
设,,则,,
∴,
∵,
∴,即,
整理得:,
∴
,
当且仅当,即,也即时,取最小值,
故答案为:.
三、简单题(20分)
11.(2024·甘肃·中考真题)计算:.
【答案】0
【详解】.
12. (2024深圳)先化简,再求值: ,其中
【答案】,
【详解】解:
=
=
=,
当时,原式=.
13.(2024·广东·模拟预测)【代数推理】代数推理指从一定条件出发,依据代数的定义、公式、运算法则、等式的性质、不等式的性质等证明已知结果或结论.
【发现问题】小明在计算时发现:对于任意两个连续的正整数m、n,它们的乘积 与较大数的和一定为较大数的平方.
(1)举例验证:当 则
(2)推理证明:小明同学做了如下的证明:
设, m、n是连续的正整数,
∴; ∵, ∴.
∴一定是正数n的平方数.
【类比猜想】小红同学提出:任意两个连续正整数的乘积与较小数的差是较小数的平方.
请你举例验证及推理证明;
【深入思考】若 (m, n为两个连续奇数, 求证:p一定是偶数.
【详解】解:类比猜想:(1)举例验证:当 则
(2)推理证明:小明同学做了如下的证明:
设, m、n是连续的正整数,
∴;
∵,
∴.
∴一定是正数的平方数.
深入思考:∵m, n为两个连续奇数,,
∴,
∴,
∴,
∴p一定是偶数.
14.(2024·河北·中考真题)情境 图1是由正方形纸片去掉一个以中心O为顶点的等腰直角三角形后得到的.
该纸片通过裁剪,可拼接为图2所示的钻石型五边形,数据如图所示.
(说明:纸片不折叠,拼接不重叠无缝隙无剩余)
操作 嘉嘉将图1所示的纸片通过裁剪,拼成了钻石型五边形.
如图3,嘉嘉沿虚线,裁剪,将该纸片剪成①,②,③三块,再按照图4所示进行拼接.根据嘉嘉的剪拼过程,解答问题:
(1)直接写出线段的长;
(2)直接写出图3中所有与线段相等的线段,并计算的长.
探究淇淇说:将图1所示纸片沿直线裁剪,剪成两块,就可以拼成钻石型五边形.
请你按照淇淇的说法设计一种方案:在图5所示纸片的边上找一点P(可以借助刻度尺或圆规),画出裁剪线(线段)的位置,并直接写出的长.
【答案】(1);(2),;的长为或.
【详解】解:如图,过作于,
结合题意可得:四边形为矩形,
∴,
由拼接可得:,
由正方形的性质可得:,
∴,,为等腰直角三角形,
∴为等腰直角三角形,
设,
∴,
∴,,
∵正方形的边长为,
∴对角线的长,
∴,
∴,
解得:,
∴;
(2)∵为等腰直角三角形,;
∴,
∴,
∵,
,
∴;
如图,以为圆心,为半径画弧交于,交于,则直线为分割线,
此时,,符合要求,
或以圆心,为半径画弧,交于,交于,则直线为分割线,
此时,,
∴,
综上:的长为或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
