北师大版九年级数学下册试题 3.9弧长及扇形的面积 同步练习(含解析)
文档属性
| 名称 | 北师大版九年级数学下册试题 3.9弧长及扇形的面积 同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-02 00:00:00 | ||
图片预览



文档简介
3.9弧长及扇形的面积
一.选择题
1.如图,,是以为直径的半圆周的三等分点,,则阴影部分的面积是
A. B. C. D.
2.道路施工部门在铺设如图所示的管道时,需要先按照其中心线计算长度后再备料.图中的管道中心线的长为(单位:
A. B. C. D.
3.已知圆的半径为6,的圆心角所对的弧长是
A. B. C. D.
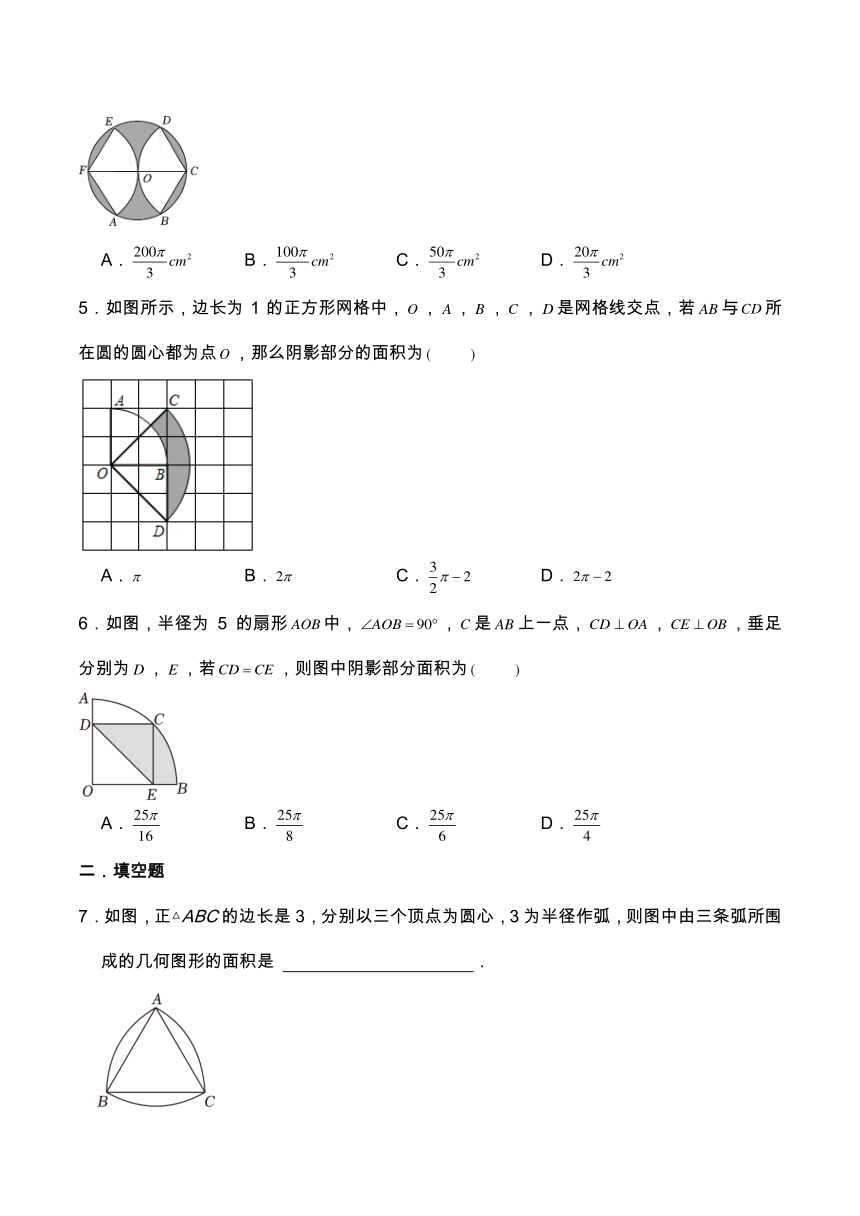
4.如图,在圆形纸板上裁剪两个扇面.具体操作如下:作的任意一条直径,以点为圆心、长为半径作圆,与相交于点、;以点为圆心、长为半径作圆,与相交于点、;连结、、、,得到两个扇形,并裁剪下来.若的半径为,则剩余纸板(图中阴影部分图形)的面积为
A. B. C. D.
5.如图所示,边长为1的正方形网格中,,,,,是网格线交点,若与所在圆的圆心都为点,那么阴影部分的面积为
A. B. C. D.
6.如图,半径为5的扇形中,,是上一点,,,垂足分别为,,若,则图中阴影部分面积为
A. B. C. D.
二.填空题
7.如图,正△ABC的边长是3,分别以三个顶点为圆心,3为半径作弧,则图中由三条弧所围成的几何图形的面积是 .
8.如图.在边长为2的正方形中,对角线、交于点,分别以点、、、为圆心,为半径画弧,弧分别与边、、、交于点、、、,则阴影部分的面积为 .
9.如图①,,表示某游乐场摩天轮上的两个轿厢.图②是其示意图,点是圆心,半径为,点,是圆上的两点,圆心角,则的长为 .(结果保留
10.如图,扇形的圆心角为,,过点作于点,以为圆心,的长为半径画弧交于点,则图中阴影部分的面积是 .
11.如图,已知等边中,,以的中点为圆心,为半径画弧,分别与、交于点、点,再以点为圆心,为半径画弧,则图中阴影部分的面积为 .
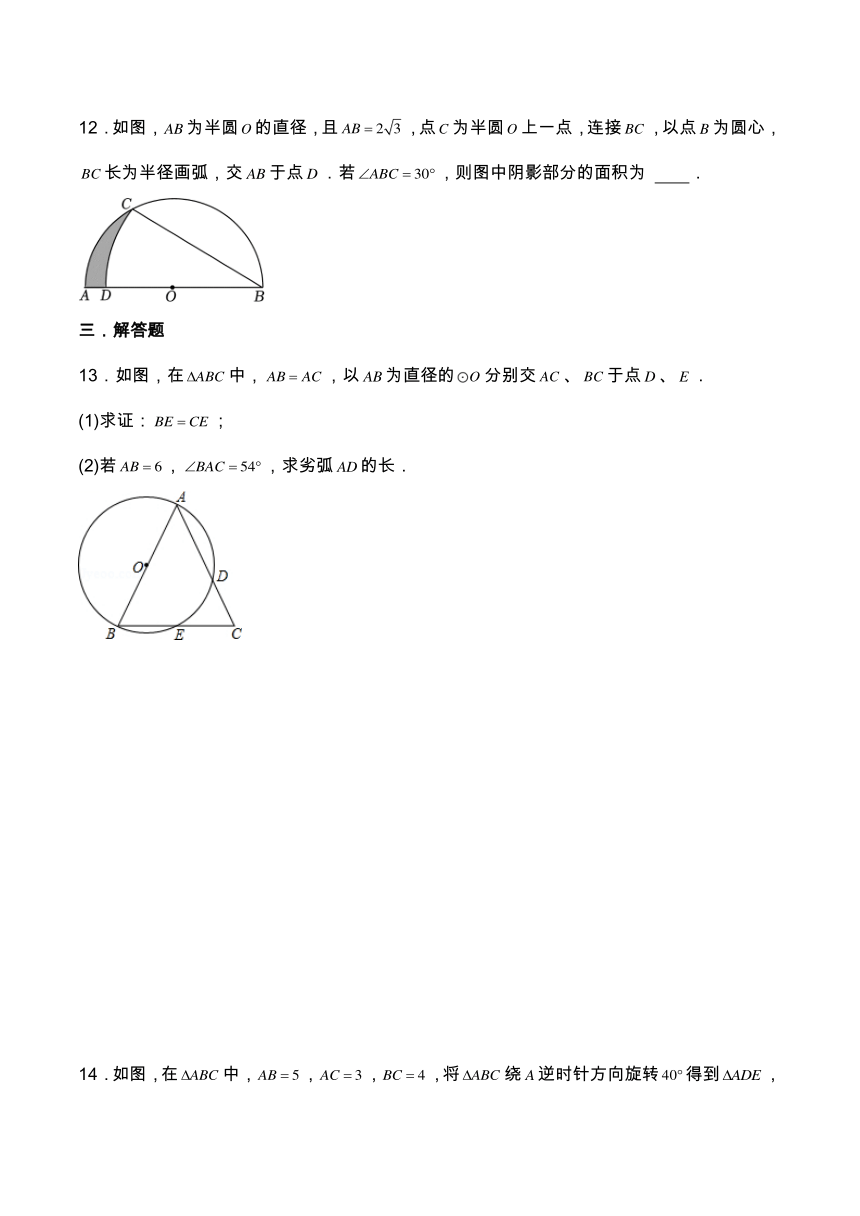
12.如图,为半圆的直径,且,点为半圆上一点,连接,以点为圆心,长为半径画弧,交于点.若,则图中阴影部分的面积为 .
三.解答题
13.如图,在中,,以为直径的分别交、于点、.
(1)求证:;
(2)若,,求劣弧的长.
14.如图,在中,,,,将绕逆时针方向旋转得到,点经过的路径为弧,求图中阴影部分的面积.
15.如图,已知是的直径,点是弧上的一点,于,点是弧的中点,交于点,交于点.
(1)判断的形状,并证明;
(2)若,.
①求的长;
②求阴影部分的面积.
16.如图,是的直径,将弦绕点顺时针旋转得到,此时点的对应点落在上,延长,交于点.
(1)证明:;
(2)若,求图中阴影部分的面积.
17.如图,在中,,以为直径的分别交、于点、.
(1)求证:;
(2)若,,求的长.
18.如图,将含角的直角三角板放入半圆中,,,三点恰好在半圆上,点是的中点,连结并延长交圆于点.
(1)求证:;
(2)若,求阴影部分的面积.
19.如图,是的直径,点是上一点,点是弧的中点,连接、、、交于点.
(1)若,求的大小;
(2)若,,求的弧长.
20.如图是由小正方形组成的网格,每个小正方形的顶点叫做格点.(画图过程用虚线,画图结果用实线).
(1)仅用无刻度的直尺,在上找三点、、(逆时针方向),使得四边形为菱形;
(2)设每个小正方形的边长为1,直接写出扇形的面积.
21.(1)问题初探,如图1,在研究圆的面积时,将圆等分成若干个扇形再拼起来,可以发现把圆等分的份数越多,拼成的图形就越接近于一个长方形,这个长方形的面积就越接近于圆的面积,其中这个长方形的长是圆周长的一半,宽等于圆的半径,故由长方形的面积推导出圆的面积,这个过程体现了“无限逼近”的数学思想.
小明在数学活动中,把一个圆等分成若干个扇形,然后拼成了一个近似的长方形,并测量出这个长方形的长是9.42厘米,那么这个圆的面积是多少平方厘米?取
(2)类比分析,生活中的易拉罐、圆形笔筒等都是一种叫做圆柱的立体图形(如图,它的上底面、下底面是两个大小相等的圆,侧面展开后是一个长方形,上、下底面之间的距离叫做圆柱的高.小明在学习了圆的面积后,也想用类似的方法研究圆柱的体积,他将一个圆柱等分成若干份,拼成了一个近似的长方体(如图,他发现把圆柱等分的份数越多,拼成的图形就越接近于一个长方体,这个长方体的体积就越接近于圆柱的体积,故由长方体的体积推导出圆柱的体积.
小明将一个半径为3分米,高为8分米的圆柱等分成若干份拼成一个近似的长方体,长方体表面积比圆柱表面积增加多少平方分米?
(3)学以致用,如图3,清雪车的前端装有滚筒,在滚筒上装有致密的刷毛,使得滚筒成为一把可以旋转的大扫帚,利用刷毛将粘结在路面上的积雪卷起,以达到除雪的目的.清雪车前端的滚筒是一个圆柱,滚筒体积为1.57立方米,滚筒横截面半径是0.5米,如果滚筒每分钟转5周.如果这次清雪要完成32970平方米的清雪任务,5辆相同的清雪车同时工作,需要多少小时完成?取
22.【问题提出】:比较代数式与的大小.
【问题探究】:要比较代数式与的大小,只要求出它们的差,若,则;若,则;若,则,反之亦然.
【问题解决】:
(1)如图,有、两种型号的钢板,型钢板的面积比型钢板大,制作某产品有两种用料方案,方案1:用4块型钢板,8块型钢板;方案2:用3块型钢板,9块型钢板.从省料角度考虑,应选哪种方案?请说明理由;
(2)有、两块长方形菜地,菜地的长为米,宽为米,菜地的长为米,宽为米,试比较两块长方形菜地周长的大小;
(3)如图,正方形的边长为,以为圆心,为半径作圆弧.以为圆心,为半径作圆弧.若图中阴影部分的面积分别为、,请你比较与的大小.
答案
一.选择题
1.
【分析】连接、,根据,是以为直径的半圆周的三等分点,可得,是等边三角形,将阴影部分的面积转化为扇形的面积求解即可.
【解答】解:如图,连接、.
,是以为直径的半圆周的三等分点,
,
又,
是等边三角形,
,,
,
,
.
故选:.
2.
【分析】根据弧长公式求出答案即可.
【解答】解:图中的管道中心线的长为,
故选:.
3.
【分析】根据弧长公式求出答案即可.
【解答】解:半径为6,圆心角为所对的弧长为.
故选:.
4.
【分析】连接,,将图中阴影部分面积拼补为扇形与扇形面积之和,进一步利用扇形的面积公式从而求出阴影部分的面积,即可求解.
【解答】解:连接,,
,的面积与弓形,的面积相等,弓形,的面积与弓形,的面积相等,
图中阴影部分的面积,
,
、是正三角形,
阴影部分的面积.
故选:.
5.
【分析】根据图形得出、、都是等腰直角三角形,根据勾股定理求出,再分别求出扇形,扇形,扇形和的面积即可.
【解答】解:,,
,
同理,,
由勾股定理得:,
阴影部分的面积
,
故选:.
6.
【分析】先连接,然后根据正方形的性质和图形,可以得到阴影部分的面积等于扇形的面积,然后代入数据计算即可.
【解答】解:连接,如图所示,
,,,
,
四边形是矩形,
,
四边形是正方形,
,和全等,
,
故选:.
二.填空题
7.
【分析】过A作AD⊥BC于D,根据等边三角形的性质得出∠ABC=∠ACB=∠BAC=60°,AB=BC=AC=3,求出BD=CD=,AD=,根据图形得出图中由三条弧所围成的几何图形的面积=3S扇形ABC﹣2S△ABC,再求出答案即可.
【解答】解:过A作AD⊥BC于D,
∵正△ABC的边长是3,
∴∠ABC=∠ACB=∠BAC=60°,AB=BC=AC=3,
∵AD⊥BC,
∴BD=CD=1cm,
∴AD===,
∴△ABC的面积=BC AD=×3×=,
∴图中由三条弧所围成的几何图形的面积是3(S扇形ABC﹣S△ABC)+S△ABC=3S扇形ABC﹣2S△ABC=3×﹣2×=π﹣,
故答案为:π﹣.
8.
【分析】根据正方形的性质得到相应条件,利用勾股定理求出,再利用计算结果即可.
【解答】解:在正方形中,
,,,
,
阴影部分的面积为:
,
故答案为:.
9.
【分析】由弧长公式:是弧长,是扇形圆心角的度数,是扇形的半径长),由此即可计算.
【解答】解:,半径为,
的长.
故答案为:.
10.
【分析】根据阴影部分的面积等于的面积减去扇形面积求即可.
【解答】解:在中,,,
,
,
,
阴影部分的面积为.
故答案为:.
11.
【分析】根据等边三角形的性质可得出,,可得,进而得出,求出弓形的面积即可.
【解答】解:如图,连接、、,
是等边三角形,
,
又,,
,
,
故答案为:.
12.
【分析】过点作于点,连接,由,得,又,得,则,故,,代入即可求得.
【解答】解:过点作于点,连接,如解图所示,
,
,
,
,
,
,
,
.
故答案为:.
三.解答题
13.(1)证明:如图,连接.
是圆的直径,
,
即.
又,
是边上的中线,
;
(2)解:,
.
又,,
,
的长为:.
14.解:将绕逆时针方向旋转得到,
,,
,,
,
.
15.(1)是等腰三角形,证明过程如下:
证明:是的直径,
,
,
,
,
为的中点,
,
,
,
,
,
是等腰三角形;
(2)解:①,
,
,
,
,
,
;
②如图,连接,
,,
是等边三角形,
,,
,
,
,
.
16.(1)证明:连接,
由旋转知,,
,,
是的直径,
,
,
,
,
;
(2)解:,
为等腰直角三角形,
,
,
.
17.(1)证明:如图,连接.
是圆的直径,
,即.
又,
是边上的中线,
;
(2)解:连接,
,
.
又,,
,
,
的长为:.
18.(1)证明:是的直径,
,
点是的中点,
,
,
,
,
;
(2)解:连接,
在中,,,
,,,
,
阴影部分的面积.
19.解:(1),
的度数为:,
的度数为:.
点是弧的中点,
的度数为:,
;
(2)连接,
是的直径,
,
,
,
,
在中,,,
,
的弧长.
20.解:(1)如图,在点的下边3格找格点,在的左方和右方分别找格点矩形和格点矩形,通过连接格点正方形的对角线即可得到其中心点,连接格点矩形的对角线即可得到其中心点,通过点,作直线,即可判断出的线段的垂直平分线,直线交于点,,依次连接,,,,则四边形是菱形.
(2)垂直平分,
,
,
,
是等边三角形,
,
扇形的面积为.
21.解:(1)根据题意得:(厘米),
(平方厘米),
答:这个圆的面积是28.26平方厘米;
(2)根据题意得:
(平方分米),
答:长方体表面积比圆柱表面积增加48平方分米;
(3)(米,
(小时),
答:需要3.5小时完成.
22.解:(1)设,两种型号的钢板的面积分别是,,
由题意,
根据方案1:用4块型钢板,8块型钢板;
则,
根据方案2:用3块型钢板,9块型钢板;
则,
,
方案2更加省料,应选方案2;
(2)根据题意得出、长方形菜地的周长分别为:,,
,
若,则,的周长大;
若,则,,的周长一样大;
若,则,的周长大;
(3)如图:
,,,
根据图形可知:,
,
,
.
一.选择题
1.如图,,是以为直径的半圆周的三等分点,,则阴影部分的面积是
A. B. C. D.
2.道路施工部门在铺设如图所示的管道时,需要先按照其中心线计算长度后再备料.图中的管道中心线的长为(单位:
A. B. C. D.
3.已知圆的半径为6,的圆心角所对的弧长是
A. B. C. D.
4.如图,在圆形纸板上裁剪两个扇面.具体操作如下:作的任意一条直径,以点为圆心、长为半径作圆,与相交于点、;以点为圆心、长为半径作圆,与相交于点、;连结、、、,得到两个扇形,并裁剪下来.若的半径为,则剩余纸板(图中阴影部分图形)的面积为
A. B. C. D.
5.如图所示,边长为1的正方形网格中,,,,,是网格线交点,若与所在圆的圆心都为点,那么阴影部分的面积为
A. B. C. D.
6.如图,半径为5的扇形中,,是上一点,,,垂足分别为,,若,则图中阴影部分面积为
A. B. C. D.
二.填空题
7.如图,正△ABC的边长是3,分别以三个顶点为圆心,3为半径作弧,则图中由三条弧所围成的几何图形的面积是 .
8.如图.在边长为2的正方形中,对角线、交于点,分别以点、、、为圆心,为半径画弧,弧分别与边、、、交于点、、、,则阴影部分的面积为 .
9.如图①,,表示某游乐场摩天轮上的两个轿厢.图②是其示意图,点是圆心,半径为,点,是圆上的两点,圆心角,则的长为 .(结果保留
10.如图,扇形的圆心角为,,过点作于点,以为圆心,的长为半径画弧交于点,则图中阴影部分的面积是 .
11.如图,已知等边中,,以的中点为圆心,为半径画弧,分别与、交于点、点,再以点为圆心,为半径画弧,则图中阴影部分的面积为 .
12.如图,为半圆的直径,且,点为半圆上一点,连接,以点为圆心,长为半径画弧,交于点.若,则图中阴影部分的面积为 .
三.解答题
13.如图,在中,,以为直径的分别交、于点、.
(1)求证:;
(2)若,,求劣弧的长.
14.如图,在中,,,,将绕逆时针方向旋转得到,点经过的路径为弧,求图中阴影部分的面积.
15.如图,已知是的直径,点是弧上的一点,于,点是弧的中点,交于点,交于点.
(1)判断的形状,并证明;
(2)若,.
①求的长;
②求阴影部分的面积.
16.如图,是的直径,将弦绕点顺时针旋转得到,此时点的对应点落在上,延长,交于点.
(1)证明:;
(2)若,求图中阴影部分的面积.
17.如图,在中,,以为直径的分别交、于点、.
(1)求证:;
(2)若,,求的长.
18.如图,将含角的直角三角板放入半圆中,,,三点恰好在半圆上,点是的中点,连结并延长交圆于点.
(1)求证:;
(2)若,求阴影部分的面积.
19.如图,是的直径,点是上一点,点是弧的中点,连接、、、交于点.
(1)若,求的大小;
(2)若,,求的弧长.
20.如图是由小正方形组成的网格,每个小正方形的顶点叫做格点.(画图过程用虚线,画图结果用实线).
(1)仅用无刻度的直尺,在上找三点、、(逆时针方向),使得四边形为菱形;
(2)设每个小正方形的边长为1,直接写出扇形的面积.
21.(1)问题初探,如图1,在研究圆的面积时,将圆等分成若干个扇形再拼起来,可以发现把圆等分的份数越多,拼成的图形就越接近于一个长方形,这个长方形的面积就越接近于圆的面积,其中这个长方形的长是圆周长的一半,宽等于圆的半径,故由长方形的面积推导出圆的面积,这个过程体现了“无限逼近”的数学思想.
小明在数学活动中,把一个圆等分成若干个扇形,然后拼成了一个近似的长方形,并测量出这个长方形的长是9.42厘米,那么这个圆的面积是多少平方厘米?取
(2)类比分析,生活中的易拉罐、圆形笔筒等都是一种叫做圆柱的立体图形(如图,它的上底面、下底面是两个大小相等的圆,侧面展开后是一个长方形,上、下底面之间的距离叫做圆柱的高.小明在学习了圆的面积后,也想用类似的方法研究圆柱的体积,他将一个圆柱等分成若干份,拼成了一个近似的长方体(如图,他发现把圆柱等分的份数越多,拼成的图形就越接近于一个长方体,这个长方体的体积就越接近于圆柱的体积,故由长方体的体积推导出圆柱的体积.
小明将一个半径为3分米,高为8分米的圆柱等分成若干份拼成一个近似的长方体,长方体表面积比圆柱表面积增加多少平方分米?
(3)学以致用,如图3,清雪车的前端装有滚筒,在滚筒上装有致密的刷毛,使得滚筒成为一把可以旋转的大扫帚,利用刷毛将粘结在路面上的积雪卷起,以达到除雪的目的.清雪车前端的滚筒是一个圆柱,滚筒体积为1.57立方米,滚筒横截面半径是0.5米,如果滚筒每分钟转5周.如果这次清雪要完成32970平方米的清雪任务,5辆相同的清雪车同时工作,需要多少小时完成?取
22.【问题提出】:比较代数式与的大小.
【问题探究】:要比较代数式与的大小,只要求出它们的差,若,则;若,则;若,则,反之亦然.
【问题解决】:
(1)如图,有、两种型号的钢板,型钢板的面积比型钢板大,制作某产品有两种用料方案,方案1:用4块型钢板,8块型钢板;方案2:用3块型钢板,9块型钢板.从省料角度考虑,应选哪种方案?请说明理由;
(2)有、两块长方形菜地,菜地的长为米,宽为米,菜地的长为米,宽为米,试比较两块长方形菜地周长的大小;
(3)如图,正方形的边长为,以为圆心,为半径作圆弧.以为圆心,为半径作圆弧.若图中阴影部分的面积分别为、,请你比较与的大小.
答案
一.选择题
1.
【分析】连接、,根据,是以为直径的半圆周的三等分点,可得,是等边三角形,将阴影部分的面积转化为扇形的面积求解即可.
【解答】解:如图,连接、.
,是以为直径的半圆周的三等分点,
,
又,
是等边三角形,
,,
,
,
.
故选:.
2.
【分析】根据弧长公式求出答案即可.
【解答】解:图中的管道中心线的长为,
故选:.
3.
【分析】根据弧长公式求出答案即可.
【解答】解:半径为6,圆心角为所对的弧长为.
故选:.
4.
【分析】连接,,将图中阴影部分面积拼补为扇形与扇形面积之和,进一步利用扇形的面积公式从而求出阴影部分的面积,即可求解.
【解答】解:连接,,
,的面积与弓形,的面积相等,弓形,的面积与弓形,的面积相等,
图中阴影部分的面积,
,
、是正三角形,
阴影部分的面积.
故选:.
5.
【分析】根据图形得出、、都是等腰直角三角形,根据勾股定理求出,再分别求出扇形,扇形,扇形和的面积即可.
【解答】解:,,
,
同理,,
由勾股定理得:,
阴影部分的面积
,
故选:.
6.
【分析】先连接,然后根据正方形的性质和图形,可以得到阴影部分的面积等于扇形的面积,然后代入数据计算即可.
【解答】解:连接,如图所示,
,,,
,
四边形是矩形,
,
四边形是正方形,
,和全等,
,
故选:.
二.填空题
7.
【分析】过A作AD⊥BC于D,根据等边三角形的性质得出∠ABC=∠ACB=∠BAC=60°,AB=BC=AC=3,求出BD=CD=,AD=,根据图形得出图中由三条弧所围成的几何图形的面积=3S扇形ABC﹣2S△ABC,再求出答案即可.
【解答】解:过A作AD⊥BC于D,
∵正△ABC的边长是3,
∴∠ABC=∠ACB=∠BAC=60°,AB=BC=AC=3,
∵AD⊥BC,
∴BD=CD=1cm,
∴AD===,
∴△ABC的面积=BC AD=×3×=,
∴图中由三条弧所围成的几何图形的面积是3(S扇形ABC﹣S△ABC)+S△ABC=3S扇形ABC﹣2S△ABC=3×﹣2×=π﹣,
故答案为:π﹣.
8.
【分析】根据正方形的性质得到相应条件,利用勾股定理求出,再利用计算结果即可.
【解答】解:在正方形中,
,,,
,
阴影部分的面积为:
,
故答案为:.
9.
【分析】由弧长公式:是弧长,是扇形圆心角的度数,是扇形的半径长),由此即可计算.
【解答】解:,半径为,
的长.
故答案为:.
10.
【分析】根据阴影部分的面积等于的面积减去扇形面积求即可.
【解答】解:在中,,,
,
,
,
阴影部分的面积为.
故答案为:.
11.
【分析】根据等边三角形的性质可得出,,可得,进而得出,求出弓形的面积即可.
【解答】解:如图,连接、、,
是等边三角形,
,
又,,
,
,
故答案为:.
12.
【分析】过点作于点,连接,由,得,又,得,则,故,,代入即可求得.
【解答】解:过点作于点,连接,如解图所示,
,
,
,
,
,
,
,
.
故答案为:.
三.解答题
13.(1)证明:如图,连接.
是圆的直径,
,
即.
又,
是边上的中线,
;
(2)解:,
.
又,,
,
的长为:.
14.解:将绕逆时针方向旋转得到,
,,
,,
,
.
15.(1)是等腰三角形,证明过程如下:
证明:是的直径,
,
,
,
,
为的中点,
,
,
,
,
,
是等腰三角形;
(2)解:①,
,
,
,
,
,
;
②如图,连接,
,,
是等边三角形,
,,
,
,
,
.
16.(1)证明:连接,
由旋转知,,
,,
是的直径,
,
,
,
,
;
(2)解:,
为等腰直角三角形,
,
,
.
17.(1)证明:如图,连接.
是圆的直径,
,即.
又,
是边上的中线,
;
(2)解:连接,
,
.
又,,
,
,
的长为:.
18.(1)证明:是的直径,
,
点是的中点,
,
,
,
,
;
(2)解:连接,
在中,,,
,,,
,
阴影部分的面积.
19.解:(1),
的度数为:,
的度数为:.
点是弧的中点,
的度数为:,
;
(2)连接,
是的直径,
,
,
,
,
在中,,,
,
的弧长.
20.解:(1)如图,在点的下边3格找格点,在的左方和右方分别找格点矩形和格点矩形,通过连接格点正方形的对角线即可得到其中心点,连接格点矩形的对角线即可得到其中心点,通过点,作直线,即可判断出的线段的垂直平分线,直线交于点,,依次连接,,,,则四边形是菱形.
(2)垂直平分,
,
,
,
是等边三角形,
,
扇形的面积为.
21.解:(1)根据题意得:(厘米),
(平方厘米),
答:这个圆的面积是28.26平方厘米;
(2)根据题意得:
(平方分米),
答:长方体表面积比圆柱表面积增加48平方分米;
(3)(米,
(小时),
答:需要3.5小时完成.
22.解:(1)设,两种型号的钢板的面积分别是,,
由题意,
根据方案1:用4块型钢板,8块型钢板;
则,
根据方案2:用3块型钢板,9块型钢板;
则,
,
方案2更加省料,应选方案2;
(2)根据题意得出、长方形菜地的周长分别为:,,
,
若,则,的周长大;
若,则,,的周长一样大;
若,则,的周长大;
(3)如图:
,,,
根据图形可知:,
,
,
.
