10.3 平行线的性质 分层训练(含答案)2024-2025学年数学沪科版七年级下册
文档属性
| 名称 | 10.3 平行线的性质 分层训练(含答案)2024-2025学年数学沪科版七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 93.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-02 14:18:54 | ||
图片预览

文档简介
10.3 平行线的性质
【基础达标】
1.如图,直线a∥b,∠1=108°,则∠2的度数是 ( )
A.72° B.82° C.92° D.108°
2.如图,把一块含有45°角的直角三角形的两个顶点放在直尺的对边上,如果∠1=20°,那么∠2的度数是 ( )
A.15° B.20° C.25° D.30°
3.如图,请分别根据已知条件进行推理,得出结论,并在括号内注明理由.
(1)如果AB∥EF,那么∠2= ,理由是 ;
(2)如果AB∥DC,那么∠3= ,理由是 ;
(3)如果AF∥BE,那么∠1+∠2= ,理由是 ;
(4)如果AF∥BE,∠4=120°,那么∠5= ,理由是 .
4.如图,∠B+∠DAB=180°,AC平分∠DAB,若∠C=50°,求∠B的度数.
【能力巩固】
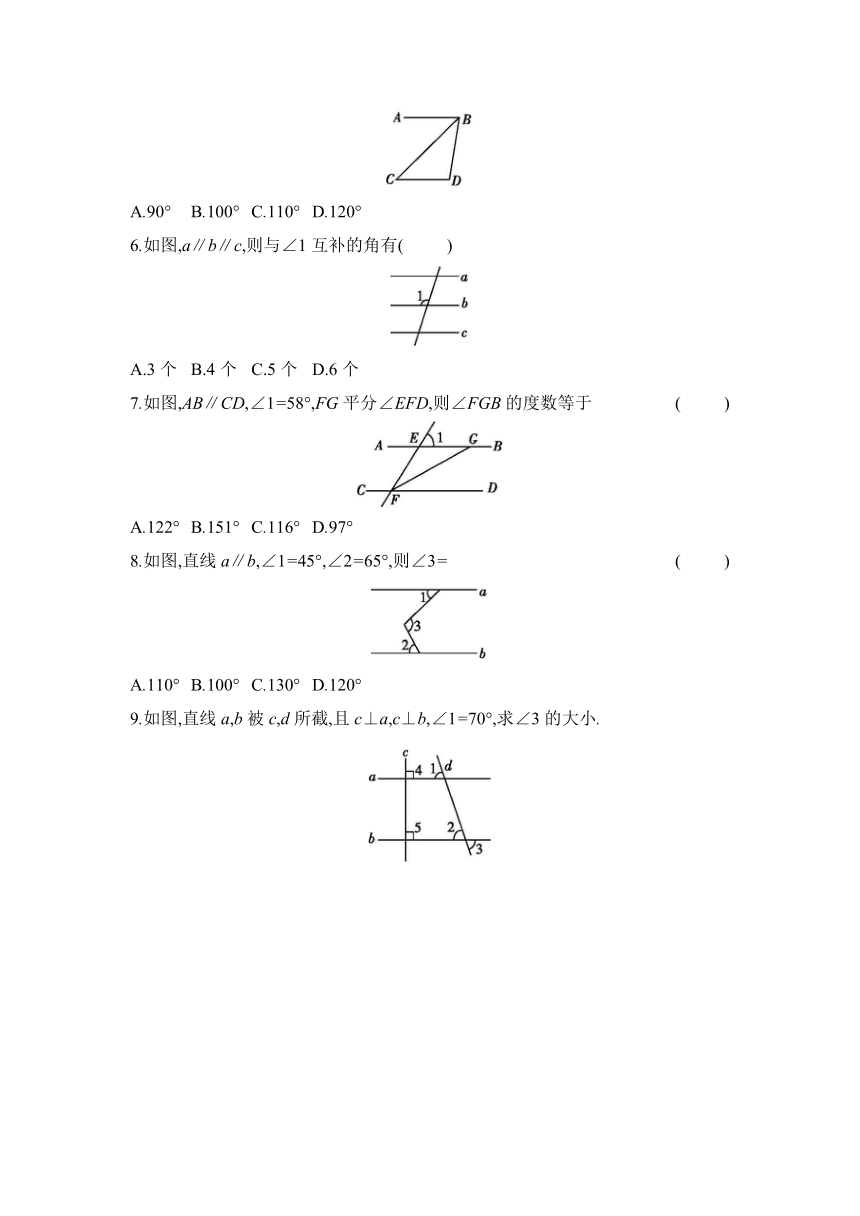
5.如图,AB∥CD,CB平分∠ABD,若∠C=40°,则∠D的度数为 ( )
A.90° B.100° C.110° D.120°
6.如图,a∥b∥c,则与∠1互补的角有( )
A.3个 B.4个 C.5个 D.6个
7.如图,AB∥CD,∠1=58°,FG平分∠EFD,则∠FGB的度数等于 ( )
A.122° B.151° C.116° D.97°
8.如图,直线a∥b,∠1=45°,∠2=65°,则∠3= ( )
A.110° B.100° C.130° D.120°
9.如图,直线a,b被c,d所截,且c⊥a,c⊥b,∠1=70°,求∠3的大小.
【素养拓展】
10.(学科融合)光线在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中是平行的光线,在空气中也是平行的.如图,∠1+∠2=103°,则∠3-∠4= .
11.【感知】如图1,点E在AB上,且CE平分∠ACD,∠1=∠2.试说明:AB∥CD.
将下列过程补充完整.
解:因为CE平分∠ACD(已知),
所以∠2=∠ (角平分线的定义).
因为∠1=∠2(已知),
所以∠1=∠ (等量代换),
所以AB∥CD( ).
【探究】如图2,点E在AB上,且CE平分∠ACD,AB∥CD.试说明:∠1=∠2.
【应用】如图3,BE平分∠DBC,A是BD上一点,过点A作AE∥BC交BE于点E,∠ABC∶∠BAE=4∶5,直接写出∠E的度数.
参考答案
基础达标作业
1.A 2.C
3.(1)∠5 两直线平行,内错角相等
(2)∠1 两平线平行,同位角相等
(3)180° 两直线平行,同旁内角互补
(4)120° 两直线平行,同位角相等
4.解:因为∠B+∠DAB=180°,所以AD∥BC,所以∠C=∠DAC=50°.
因为AC平分∠DAB,所以∠DAB=2∠DAC=100°.
因为∠B+∠DAB=180°,所以∠B=80°.
能力巩固作业
5.B 6.D 7.B 8.A
9.解:因为c⊥a,c⊥b,
所以∠4=∠5=90°,所以a∥b.
因为∠1=70°,所以∠1=∠2=70°,
所以∠3=∠2=70°.
素养拓展作业
10.77°
11.解:【感知】DCE;DCE;内错角相等,两直线平行.
【探究】因为CE平分∠ACD,所以∠2=∠DCE.
因为AB∥CD,所以∠1=∠DCE,所以∠1=∠2.
【应用】因为BE平分∠DBC,所以∠ABE=∠CBE.
因为AE∥BC,所以∠ABC+∠BAE=180°,∠E=∠CBE.
因为∠ABC∶∠BAE=4∶5,所以∠ABC=80°,
所以∠CBE=40°,所以∠E=∠CBE=40°.
【基础达标】
1.如图,直线a∥b,∠1=108°,则∠2的度数是 ( )
A.72° B.82° C.92° D.108°
2.如图,把一块含有45°角的直角三角形的两个顶点放在直尺的对边上,如果∠1=20°,那么∠2的度数是 ( )
A.15° B.20° C.25° D.30°
3.如图,请分别根据已知条件进行推理,得出结论,并在括号内注明理由.
(1)如果AB∥EF,那么∠2= ,理由是 ;
(2)如果AB∥DC,那么∠3= ,理由是 ;
(3)如果AF∥BE,那么∠1+∠2= ,理由是 ;
(4)如果AF∥BE,∠4=120°,那么∠5= ,理由是 .
4.如图,∠B+∠DAB=180°,AC平分∠DAB,若∠C=50°,求∠B的度数.
【能力巩固】
5.如图,AB∥CD,CB平分∠ABD,若∠C=40°,则∠D的度数为 ( )
A.90° B.100° C.110° D.120°
6.如图,a∥b∥c,则与∠1互补的角有( )
A.3个 B.4个 C.5个 D.6个
7.如图,AB∥CD,∠1=58°,FG平分∠EFD,则∠FGB的度数等于 ( )
A.122° B.151° C.116° D.97°
8.如图,直线a∥b,∠1=45°,∠2=65°,则∠3= ( )
A.110° B.100° C.130° D.120°
9.如图,直线a,b被c,d所截,且c⊥a,c⊥b,∠1=70°,求∠3的大小.
【素养拓展】
10.(学科融合)光线在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中是平行的光线,在空气中也是平行的.如图,∠1+∠2=103°,则∠3-∠4= .
11.【感知】如图1,点E在AB上,且CE平分∠ACD,∠1=∠2.试说明:AB∥CD.
将下列过程补充完整.
解:因为CE平分∠ACD(已知),
所以∠2=∠ (角平分线的定义).
因为∠1=∠2(已知),
所以∠1=∠ (等量代换),
所以AB∥CD( ).
【探究】如图2,点E在AB上,且CE平分∠ACD,AB∥CD.试说明:∠1=∠2.
【应用】如图3,BE平分∠DBC,A是BD上一点,过点A作AE∥BC交BE于点E,∠ABC∶∠BAE=4∶5,直接写出∠E的度数.
参考答案
基础达标作业
1.A 2.C
3.(1)∠5 两直线平行,内错角相等
(2)∠1 两平线平行,同位角相等
(3)180° 两直线平行,同旁内角互补
(4)120° 两直线平行,同位角相等
4.解:因为∠B+∠DAB=180°,所以AD∥BC,所以∠C=∠DAC=50°.
因为AC平分∠DAB,所以∠DAB=2∠DAC=100°.
因为∠B+∠DAB=180°,所以∠B=80°.
能力巩固作业
5.B 6.D 7.B 8.A
9.解:因为c⊥a,c⊥b,
所以∠4=∠5=90°,所以a∥b.
因为∠1=70°,所以∠1=∠2=70°,
所以∠3=∠2=70°.
素养拓展作业
10.77°
11.解:【感知】DCE;DCE;内错角相等,两直线平行.
【探究】因为CE平分∠ACD,所以∠2=∠DCE.
因为AB∥CD,所以∠1=∠DCE,所以∠1=∠2.
【应用】因为BE平分∠DBC,所以∠ABE=∠CBE.
因为AE∥BC,所以∠ABC+∠BAE=180°,∠E=∠CBE.
因为∠ABC∶∠BAE=4∶5,所以∠ABC=80°,
所以∠CBE=40°,所以∠E=∠CBE=40°.
