5.7 切线长定理(学案,含答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
第五章 圆
7 切线长定理
列清单·划重点
知识点1 尺规作图:过圆外一点 P,作⊙O的切线.
已知:⊙O和⊙O外一点 P;
求作:过点 P 作⊙O 的切线.
作法:①连接OP;
②作线段 OP 的垂直平分线MN,垂足为点C;
③以点 C 为圆心,CO为半径画圆,交⊙O于点A,B;
④作直线 PA,PB,则直线 PA,PB 即为所求作.
知识点2 切线长
过圆外一点作圆的切线,这点和切点之间的线段长叫做这点到圆的 .
知识点3 切线长定理
1.从圆外一点引圆的两条切线,它们的 相等.
2.数学符号语言:
∵PA,PB 是⊙O的两条切线,A,B 为切点,∴PA=PB.
注意
(1)切线是直线,没有长度,不能度量.定理中的切线长相等,是指这点与两切点之间的线段长相等;
(2)利用切线长定理可以证明线段相等、角相等、弧相等以及垂直关系.如图所示,还可得AD=BD,∠APO=∠BPO,AC=BC,△PAB为等腰三角形等.
明考点·识方法
考点1 切线长定理的应用
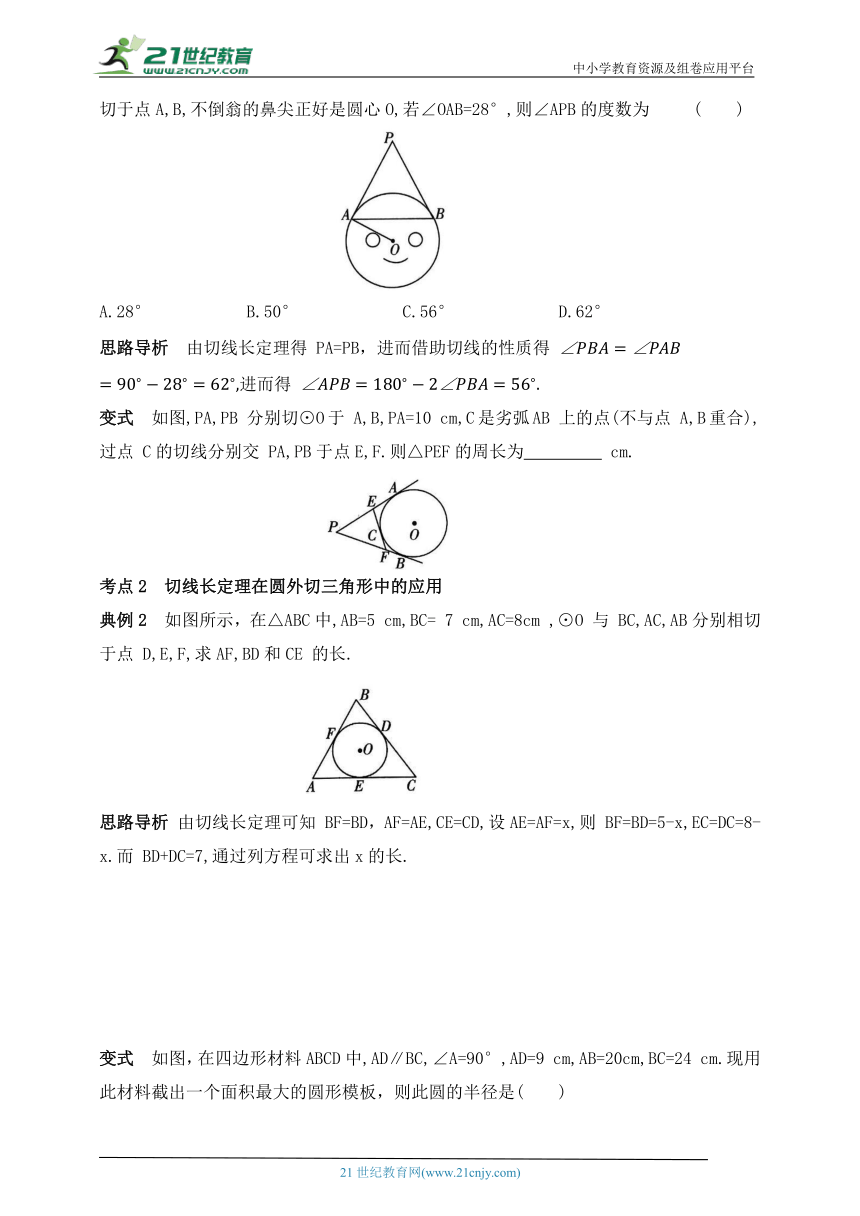
典例1 如图是不倒翁的主视图,不倒翁的圆形 脸 恰 好 与 帽子 边沿PA,PB分别相切于点A,B,不倒翁的鼻尖正好是圆心O,若∠OAB=28°,则∠APB的度数为 ( )
A.28° B.50° C.56° D.62°
思路导析 由切线长定理得 PA=PB,进而借助切线的性质得
进而得
变式 如图,PA,PB 分别切⊙O于 A,B,PA=10 cm,C是劣弧AB 上的点(不与点 A,B重合),过点 C的切线分别交 PA,PB于点E,F.则△PEF的周长为 cm.
考点2 切线长定理在圆外切三角形中的应用
典例2 如图所示,在△ABC中,AB=5 cm,BC= 7 cm,AC=8cm ,⊙O 与 BC,AC,AB分别相切于点 D,E,F,求AF,BD和CE 的长.
思路导析 由切线长定理可知 BF=BD,AF=AE,CE=CD,设AE=AF=x,则 BF=BD=5-x,EC=DC=8-x.而 BD+DC=7,通过列方程可求出x的长.
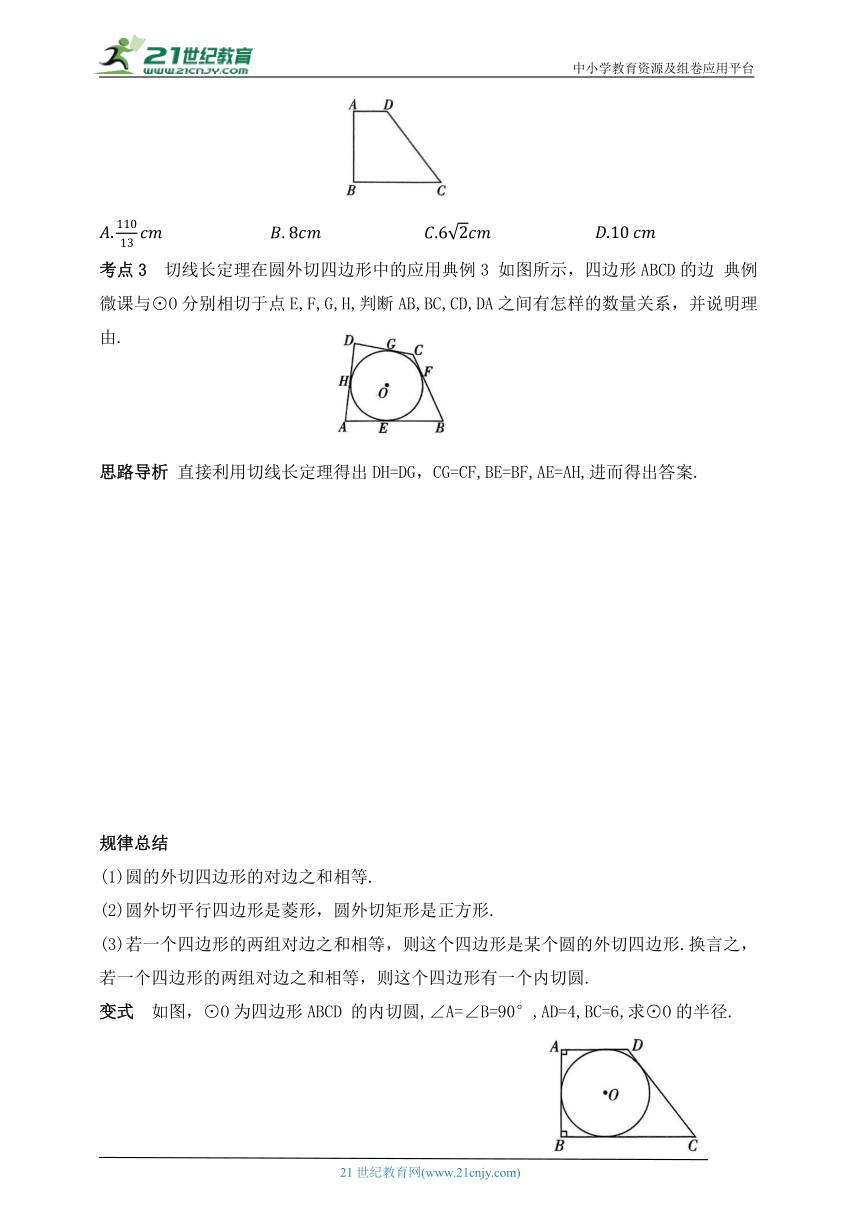
变式 如图,在四边形材料ABCD中,AD∥BC,∠A=90°,AD=9 cm,AB=20cm,BC=24 cm.现用此材料截出一个面积最大的圆形模板,则此圆的半径是( )
考点3 切线长定理在圆外切四边形中的应用典例3 如图所示,四边形ABCD的边 典例微课与⊙O分别相切于点E,F,G,H,判断AB,BC,CD,DA之间有怎样的数量关系,并说明理由.
思路导析 直接利用切线长定理得出DH=DG,CG=CF,BE=BF,AE=AH,进而得出答案.
规律总结
(1)圆的外切四边形的对边之和相等.
(2)圆外切平行四边形是菱形,圆外切矩形是正方形.
(3)若一个四边形的两组对边之和相等,则这个四边形是某个圆的外切四边形.换言之,若一个四边形的两组对边之和相等,则这个四边形有一个内切圆.
变式 如图,⊙O为四边形ABCD 的内切圆,∠A=∠B=90°,AD=4,BC=6,求⊙O的半径.
当堂测·夯基础
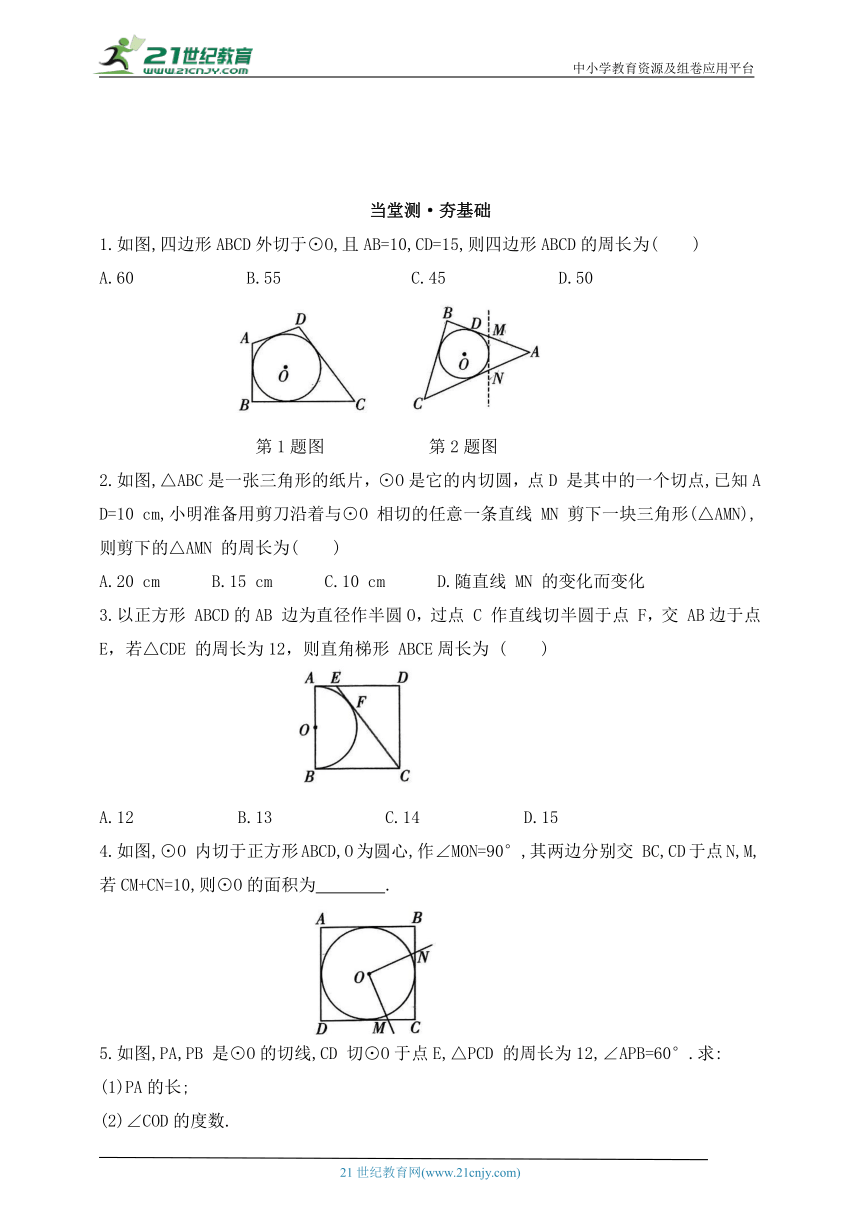
1.如图,四边形ABCD外切于⊙O,且AB=10,CD=15,则四边形ABCD的周长为( )
A.60 B.55 C.45 D.50
第1题图 第2题图
2.如图,△ABC是一张三角形的纸片,⊙O是它的内切圆,点D 是其中的一个切点,已知AD=10 cm,小明准备用剪刀沿着与⊙O 相切的任意一条直线 MN 剪下一块三角形(△AMN),则剪下的△AMN 的周长为( )
A.20 cm B.15 cm C.10 cm D.随直线 MN 的变化而变化
3.以正方形 ABCD的AB 边为直径作半圆O,过点 C 作直线切半圆于点 F,交 AB边于点E,若△CDE 的周长为12,则直角梯形 ABCE周长为 ( )
A.12 B.13 C.14 D.15
4.如图,⊙O 内切于正方形ABCD,O为圆心,作∠MON=90°,其两边分别交 BC,CD于点N,M,若CM+CN=10,则⊙O的面积为 .
5.如图,PA,PB 是⊙O的切线,CD 切⊙O于点E,△PCD 的周长为12,∠APB=60°.求:
(1)PA的长;
(2)∠COD的度数.
参考答案
【列清单·划重点】
知识点 2 切线长
知识点 3 1.切线长
【明考点·识方法】
典例1 C 解析:∵PA,PB分别切⊙O于点A,B,∴PA=PB,OA⊥PA,
变式 20
典例2 解:∵⊙O 与 BC,AC,AB 分别相切于点D,E,F,
∴AE=AF,BF=BD,EC=DC.
设AE=AF=x cm,则 BF=BD=(5-x) cm,CE=DC=(8-x) cm,
∴BD+DC=(5-x)+(8-x)=7.解得x=3,即AF=3cm,
∴BD=BF=5-3=2(cm),CE=AC-AE=8-3=5(cm).
变式 B 解析:如图所示,延长 BA 交CD延长线于点 E,当这个圆为△BCE 的内切圆时,此圆的面积最大,
∵AD∥BC,∠BAD=90°,∴△EAD∽△EBC,∠ABC=90°,
即 解得 EA=12,∴EB=32cm,
.
设这个圆的圆心为点 O,与EB,BC,EC分别相切于点F,G,H,连接OF,OG,OH,OE,OB,OC,∴OF=OG=OH,
S△EOC,
∴24×32=(24+32+40)·OF,∴OF=8cm,
∴此圆的半径为 8cm .
典例3 解:AD+BC=CD+AB,理由:
∵四边形ABCD的边与⊙O分别相切于点E,F,G,H,
∴DH=DG,CG=CF,BE=BF,AE=AH.
∴AH+DH+CF+BF=DG+GC+AE+BE,即AD+BC=CD+AB.
变式 解:过点D作DG⊥BC于点G,设AD与圆的切点为H,DC与圆的切点为F,BC与圆的切点为E,AB与圆的切点为M,连接OM,OE,OH,如图,则OH⊥AD,OE⊥BC,OM⊥AB,OH=OE=OM,
∵∠A=∠B=90°,∴四边形 AMOH,四边形 BMOE 都是正方形,
∴∠HOM=∠MOE=90°,∴∠EOH=180°,∴点 E,O,H三点共线,
∴四边形 HEGD 是矩形,∴BG=AD=4,CG=BC-BG=6-4=2,
∵点 E,F,H 是切点,∴DF=DH,CF=CE,
设⊙O 半径为R,则 BE=AH=OM=R,DG=HE=2R,∴CE=CF=6-R,DF=DH=4-R,
解得
所以⊙O的半径为
【当堂测·夯基础】
1. D 2. A 3. C
4.25π 解析:设⊙O与正方形ABCD 的边CD 相切于点E,与 BC相切于点F,连接OE,OF,则四边形OECF 是正方形,∴CF=CE=OE=OF,∠OEM=∠OFN=
∵∠MON=90°,∴∠EOM=∠FON,∴△OEM≌△OFN(ASA),
∴EM=NF,∴CM+CN=CE+CF=10,∴OE=5,
∴⊙O 的面积为 25π.
5.解:(1)∵CA,CE都是圆O的切线,∴CA=CE,
同理DE=DB,PA=PB,
∴三角形 PCD 的周长 = PD+CD+PC=PD+PC+CA+BD=PA+PB=2PA=12,
即 PA 的长为6;
(2)∵∠P=60°,∴∠PCE+∠PDE=120°,
∵CA,CE是圆O的切线,
同理:∠CDB)=120°,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 圆
7 切线长定理
列清单·划重点
知识点1 尺规作图:过圆外一点 P,作⊙O的切线.
已知:⊙O和⊙O外一点 P;
求作:过点 P 作⊙O 的切线.
作法:①连接OP;
②作线段 OP 的垂直平分线MN,垂足为点C;
③以点 C 为圆心,CO为半径画圆,交⊙O于点A,B;
④作直线 PA,PB,则直线 PA,PB 即为所求作.
知识点2 切线长
过圆外一点作圆的切线,这点和切点之间的线段长叫做这点到圆的 .
知识点3 切线长定理
1.从圆外一点引圆的两条切线,它们的 相等.
2.数学符号语言:
∵PA,PB 是⊙O的两条切线,A,B 为切点,∴PA=PB.
注意
(1)切线是直线,没有长度,不能度量.定理中的切线长相等,是指这点与两切点之间的线段长相等;
(2)利用切线长定理可以证明线段相等、角相等、弧相等以及垂直关系.如图所示,还可得AD=BD,∠APO=∠BPO,AC=BC,△PAB为等腰三角形等.
明考点·识方法
考点1 切线长定理的应用
典例1 如图是不倒翁的主视图,不倒翁的圆形 脸 恰 好 与 帽子 边沿PA,PB分别相切于点A,B,不倒翁的鼻尖正好是圆心O,若∠OAB=28°,则∠APB的度数为 ( )
A.28° B.50° C.56° D.62°
思路导析 由切线长定理得 PA=PB,进而借助切线的性质得
进而得
变式 如图,PA,PB 分别切⊙O于 A,B,PA=10 cm,C是劣弧AB 上的点(不与点 A,B重合),过点 C的切线分别交 PA,PB于点E,F.则△PEF的周长为 cm.
考点2 切线长定理在圆外切三角形中的应用
典例2 如图所示,在△ABC中,AB=5 cm,BC= 7 cm,AC=8cm ,⊙O 与 BC,AC,AB分别相切于点 D,E,F,求AF,BD和CE 的长.
思路导析 由切线长定理可知 BF=BD,AF=AE,CE=CD,设AE=AF=x,则 BF=BD=5-x,EC=DC=8-x.而 BD+DC=7,通过列方程可求出x的长.
变式 如图,在四边形材料ABCD中,AD∥BC,∠A=90°,AD=9 cm,AB=20cm,BC=24 cm.现用此材料截出一个面积最大的圆形模板,则此圆的半径是( )
考点3 切线长定理在圆外切四边形中的应用典例3 如图所示,四边形ABCD的边 典例微课与⊙O分别相切于点E,F,G,H,判断AB,BC,CD,DA之间有怎样的数量关系,并说明理由.
思路导析 直接利用切线长定理得出DH=DG,CG=CF,BE=BF,AE=AH,进而得出答案.
规律总结
(1)圆的外切四边形的对边之和相等.
(2)圆外切平行四边形是菱形,圆外切矩形是正方形.
(3)若一个四边形的两组对边之和相等,则这个四边形是某个圆的外切四边形.换言之,若一个四边形的两组对边之和相等,则这个四边形有一个内切圆.
变式 如图,⊙O为四边形ABCD 的内切圆,∠A=∠B=90°,AD=4,BC=6,求⊙O的半径.
当堂测·夯基础
1.如图,四边形ABCD外切于⊙O,且AB=10,CD=15,则四边形ABCD的周长为( )
A.60 B.55 C.45 D.50
第1题图 第2题图
2.如图,△ABC是一张三角形的纸片,⊙O是它的内切圆,点D 是其中的一个切点,已知AD=10 cm,小明准备用剪刀沿着与⊙O 相切的任意一条直线 MN 剪下一块三角形(△AMN),则剪下的△AMN 的周长为( )
A.20 cm B.15 cm C.10 cm D.随直线 MN 的变化而变化
3.以正方形 ABCD的AB 边为直径作半圆O,过点 C 作直线切半圆于点 F,交 AB边于点E,若△CDE 的周长为12,则直角梯形 ABCE周长为 ( )
A.12 B.13 C.14 D.15
4.如图,⊙O 内切于正方形ABCD,O为圆心,作∠MON=90°,其两边分别交 BC,CD于点N,M,若CM+CN=10,则⊙O的面积为 .
5.如图,PA,PB 是⊙O的切线,CD 切⊙O于点E,△PCD 的周长为12,∠APB=60°.求:
(1)PA的长;
(2)∠COD的度数.
参考答案
【列清单·划重点】
知识点 2 切线长
知识点 3 1.切线长
【明考点·识方法】
典例1 C 解析:∵PA,PB分别切⊙O于点A,B,∴PA=PB,OA⊥PA,
变式 20
典例2 解:∵⊙O 与 BC,AC,AB 分别相切于点D,E,F,
∴AE=AF,BF=BD,EC=DC.
设AE=AF=x cm,则 BF=BD=(5-x) cm,CE=DC=(8-x) cm,
∴BD+DC=(5-x)+(8-x)=7.解得x=3,即AF=3cm,
∴BD=BF=5-3=2(cm),CE=AC-AE=8-3=5(cm).
变式 B 解析:如图所示,延长 BA 交CD延长线于点 E,当这个圆为△BCE 的内切圆时,此圆的面积最大,
∵AD∥BC,∠BAD=90°,∴△EAD∽△EBC,∠ABC=90°,
即 解得 EA=12,∴EB=32cm,
.
设这个圆的圆心为点 O,与EB,BC,EC分别相切于点F,G,H,连接OF,OG,OH,OE,OB,OC,∴OF=OG=OH,
S△EOC,
∴24×32=(24+32+40)·OF,∴OF=8cm,
∴此圆的半径为 8cm .
典例3 解:AD+BC=CD+AB,理由:
∵四边形ABCD的边与⊙O分别相切于点E,F,G,H,
∴DH=DG,CG=CF,BE=BF,AE=AH.
∴AH+DH+CF+BF=DG+GC+AE+BE,即AD+BC=CD+AB.
变式 解:过点D作DG⊥BC于点G,设AD与圆的切点为H,DC与圆的切点为F,BC与圆的切点为E,AB与圆的切点为M,连接OM,OE,OH,如图,则OH⊥AD,OE⊥BC,OM⊥AB,OH=OE=OM,
∵∠A=∠B=90°,∴四边形 AMOH,四边形 BMOE 都是正方形,
∴∠HOM=∠MOE=90°,∴∠EOH=180°,∴点 E,O,H三点共线,
∴四边形 HEGD 是矩形,∴BG=AD=4,CG=BC-BG=6-4=2,
∵点 E,F,H 是切点,∴DF=DH,CF=CE,
设⊙O 半径为R,则 BE=AH=OM=R,DG=HE=2R,∴CE=CF=6-R,DF=DH=4-R,
解得
所以⊙O的半径为
【当堂测·夯基础】
1. D 2. A 3. C
4.25π 解析:设⊙O与正方形ABCD 的边CD 相切于点E,与 BC相切于点F,连接OE,OF,则四边形OECF 是正方形,∴CF=CE=OE=OF,∠OEM=∠OFN=
∵∠MON=90°,∴∠EOM=∠FON,∴△OEM≌△OFN(ASA),
∴EM=NF,∴CM+CN=CE+CF=10,∴OE=5,
∴⊙O 的面积为 25π.
5.解:(1)∵CA,CE都是圆O的切线,∴CA=CE,
同理DE=DB,PA=PB,
∴三角形 PCD 的周长 = PD+CD+PC=PD+PC+CA+BD=PA+PB=2PA=12,
即 PA 的长为6;
(2)∵∠P=60°,∴∠PCE+∠PDE=120°,
∵CA,CE是圆O的切线,
同理:∠CDB)=120°,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
