5.8 正多边形和圆(学案,含答案)
文档属性
| 名称 | 5.8 正多边形和圆(学案,含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 485.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-02 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第五章 圆
8 正多边形和圆
列清单·划重点
知识点1 圆的内接正n边形
把⊙O分成n等份,顺次连接这 n个等分点,便得到了一个⊙O的内接 .
知识点2 正多边形的有关概念
1.正多边形的中心:一个正 n边形一共有n条对称轴,正多边形的对称轴相交于一点,这个点到正多边形各边的距离都相等,到正多边形各顶点的距离也都相等,这个点叫做 .
2.正多边形的外接圆:以正多边形的中心为圆心,以中心到一个顶点的距离为半径作圆,便得到这个正多边形的 .正多边形的外接圆的 叫做正多边形的半径.
3.正多边形的内切圆:以正多边形的中心为圆心,以中心到一条边的距离为半径作圆,便得到这个正多边形的 .正多边形的内切圆的半径叫做正多边形的 .
4.正多边形的中心角:正多边形每一条边所对外接圆的圆心角叫做正多边形的 .
知识点3 与正多边形有关的计算
计算正多边形的边长、半径、边心距、中心角、周长和面积之间的关系的问题时,通常归结为解三角形的问题.
如图所示,设正 n边形的半径为R,边心距为r,边长为a,半中心角为θ,周长为p,面积为S,则
(1)正n边形的中心角与它的每个外角相等,都等于
知识点4 用尺规作正多边形
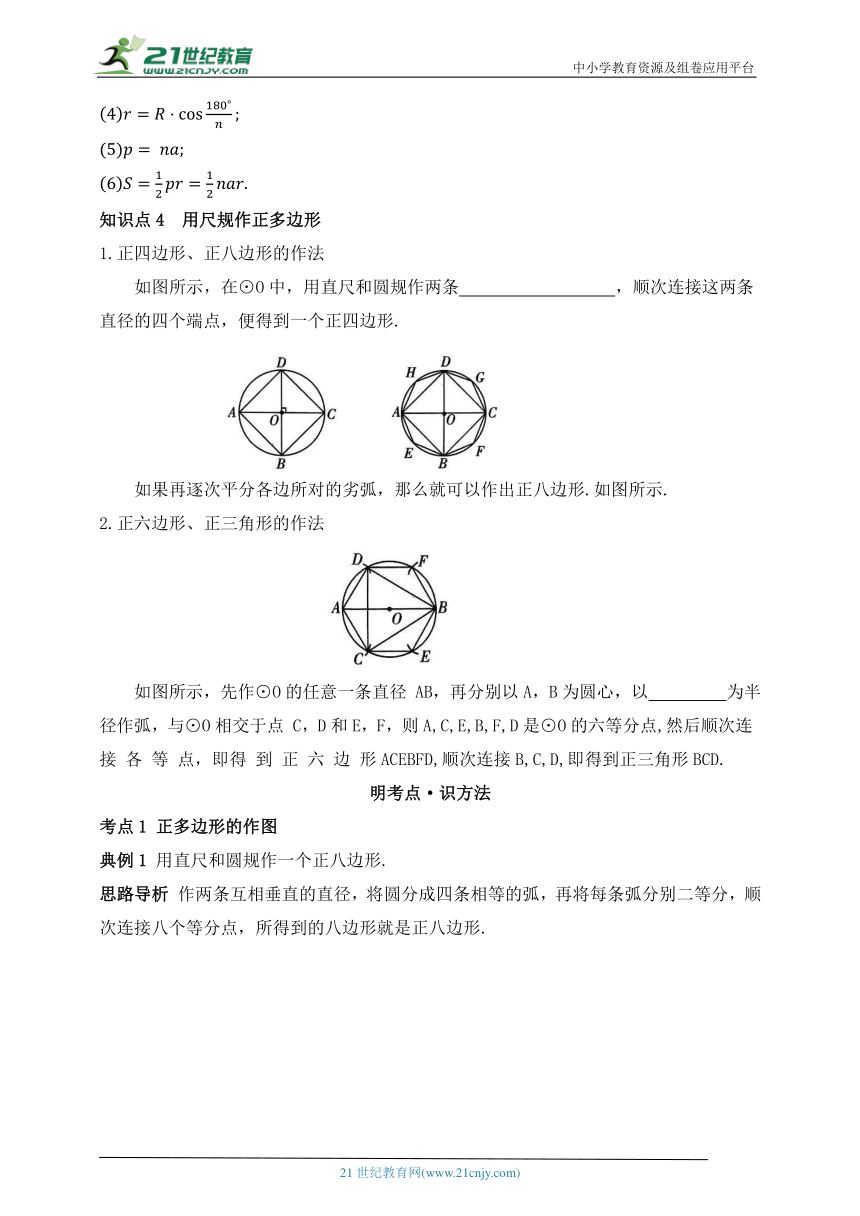
1.正四边形、正八边形的作法
如图所示,在⊙O中,用直尺和圆规作两条 ,顺次连接这两条直径的四个端点,便得到一个正四边形.
如果再逐次平分各边所对的劣弧,那么就可以作出正八边形.如图所示.
2.正六边形、正三角形的作法
如图所示,先作⊙O的任意一条直径 AB,再分别以A,B为圆心,以 为半径作弧,与⊙O相交于点 C,D和E,F,则A,C,E,B,F,D是⊙O的六等分点,然后顺次连 接 各 等 点,即得 到 正 六 边 形ACEBFD,顺次连接B,C,D,即得到正三角形BCD.
明考点·识方法
考点1 正多边形的作图
典例1 用直尺和圆规作一个正八边形.
思路导析 作两条互相垂直的直径,将圆分成四条相等的弧,再将每条弧分别二等分,顺次连接八个等分点,所得到的八边形就是正八边形.
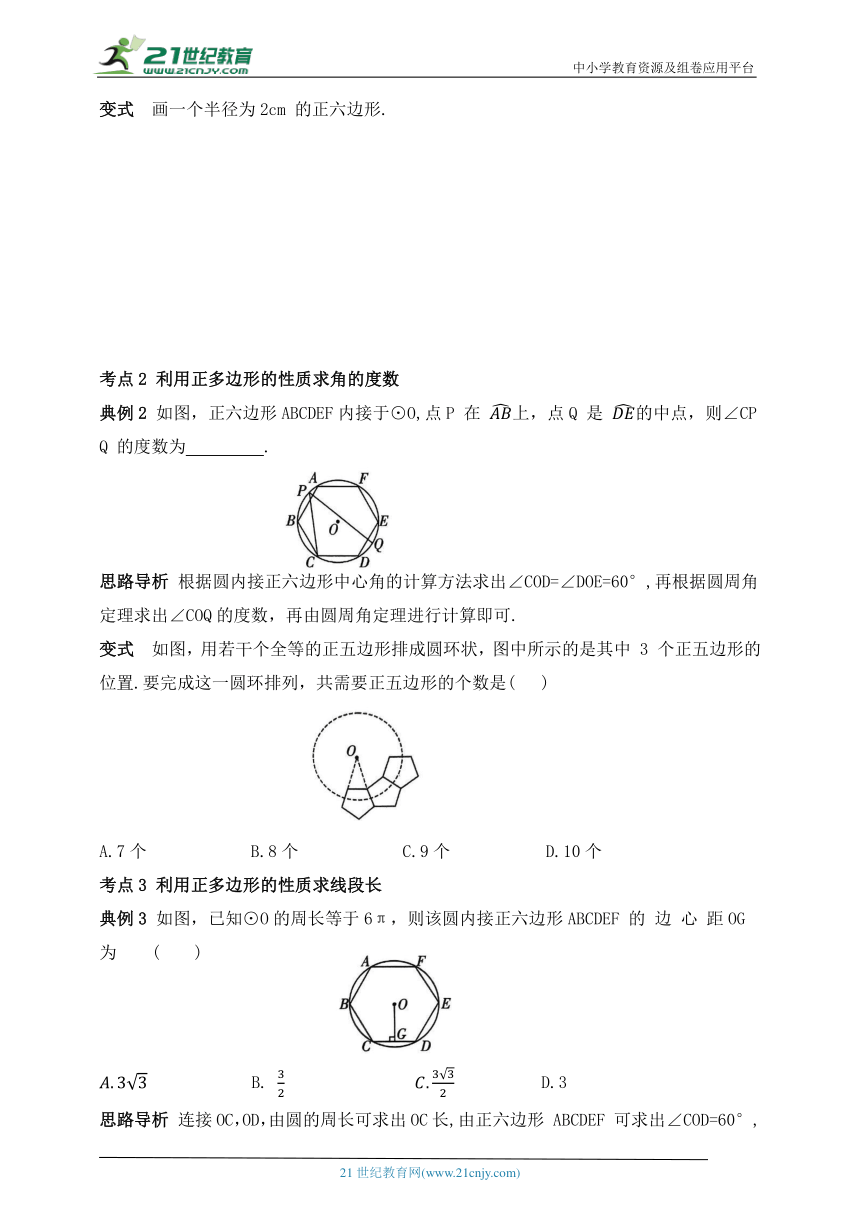
变式 画一个半径为2cm 的正六边形.
考点2 利用正多边形的性质求角的度数
典例2 如图,正六边形ABCDEF内接于⊙O,点P 在 上,点Q 是 的中点,则∠CPQ 的度数为 .
思路导析 根据圆内接正六边形中心角的计算方法求出∠COD=∠DOE=60°,再根据圆周角定理求出∠COQ的度数,再由圆周角定理进行计算即可.
变式 如图,用若干个全等的正五边形排成圆环状,图中所示的是其中 3 个正五边形的位置.要完成这一圆环排列,共需要正五边形的个数是( )
A.7个 B.8个 C.9个 D.10个
考点3 利用正多边形的性质求线段长
典例3 如图,已知⊙O的周长等于6π,则该圆内接正六边形ABCDEF 的 边 心 距OG 为 ( )
B. D.3
思路导析 连接OC,OD,由圆的周长可求出OC长,由正六边形 ABCDEF 可求出∠COD=60°,进而可求出∠COG=30°,根据30°角的锐角三角函数值即可求出边心距OG的长.
规律总结
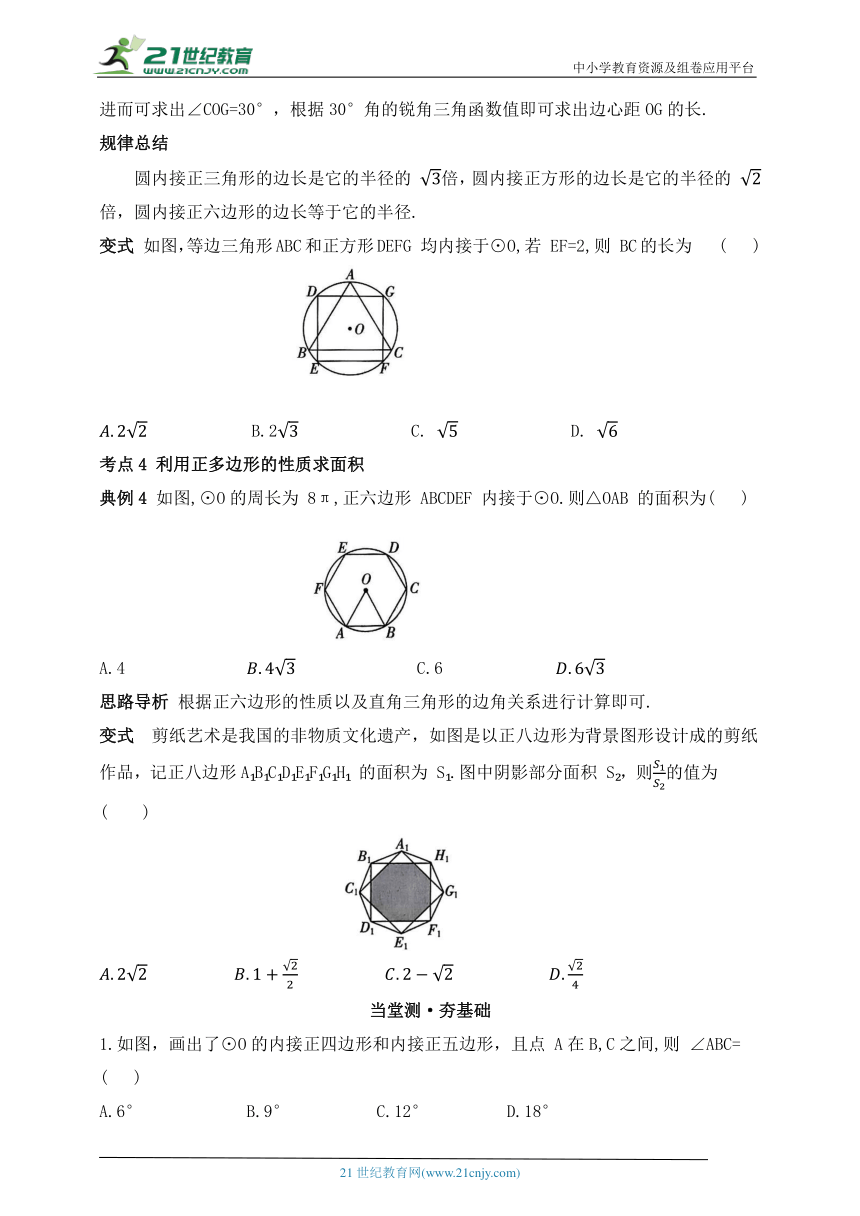
圆内接正三角形的边长是它的半径的 倍,圆内接正方形的边长是它的半径的 倍,圆内接正六边形的边长等于它的半径.
变式 如图,等边三角形ABC和正方形DEFG 均内接于⊙O,若 EF=2,则 BC的长为 ( )
B.2 C. D.
考点4 利用正多边形的性质求面积
典例4 如图,⊙O的周长为 8π,正六边形 ABCDEF 内接于⊙O.则△OAB 的面积为( )
A.4 C.6
思路导析 根据正六边形的性质以及直角三角形的边角关系进行计算即可.
变式 剪纸艺术是我国的非物质文化遗产,如图是以正八边形为背景图形设计成的剪纸作品,记正八边形A B C D E F G H 的面积为 S .图中阴影部分面积 S ,则的值为 ( )
当堂测·夯基础
1.如图,画出了⊙O的内接正四边形和内接正五边形,且点 A在B,C之间,则 ∠ABC= ( )
A.6° B.9° C.12° D.18°
第1题图 第2题图
2.如图,电子屏幕上有边长为1 的正六边形 ABCDEF,红色光点和蓝色光点会按规则在六个顶点上闪亮.规则为:红点按顺时针方向每秒一个顶点依次闪亮(例如,经过1 秒由点A 亮变为点 F 亮),蓝点按逆时针方向每秒隔1个顶点闪亮(例如,经过1 秒由点A亮变为点 C 亮).若一开始,红点在 A处,蓝点在 B 处同时开始闪亮,则经过751秒后,两个闪亮的顶点之间的距离是( )
A.0 B.1 C. D.2
3.如图,正方形ABCD内接于⊙O,等边△AEF的顶点E,F分别在BC,CD上,EF交BC,CD于点G,H,则 的值等于( )
A. B. C. D.2
4.苯(分子式为C H )的环状结构是由德国化学家凯库勒提出的.随着研究的不断深入,发现苯分子中的6个碳原子组成了一个完美的正六边形(如图1),图2 是其平面示意图,点O为正六边形ABCDEF 的中心,则∠CBF-∠COD 的度数为 ( )
A.30° B.45° C.60° D.90°
5.某厂家要设计一个装彩铅的纸盒,已知每支笔形状、大小相同,底面均为正六边形,六边形的边长为1 cm,目前厂家提供了圆形和等边三角形两种作为底面的设计方案,我们以6支彩铅为例,可以设计如图收纳方案一和收纳方案二,你认为底面积更小的是 ,两种方案底面积差为 (结果保留根号).
参考答案
【列清单·划重点】
知识点1 正n边形
知识点2 1.正多边形的中心 2.外接圆半径 3.内切圆 边心距 4.中心角
知识点4 1.相互垂直的直径 2. OA
【明考点·识方法】
典例1 解:步骤如下:
(1)任意作一个圆,记作⊙O;
(2)用直尺作⊙O的一条直径AE;
(3)用直尺和圆规作 AE 的垂直平分线与⊙O交于C,G两点;
(4)用圆规将 AC,CE,EG,GA分别二等分,顺次连接上述八个等分点(如图所示).那么八边形ABCDEFGH 就是所要求作的正八边形.
变式 解:如图所示,作半径是2cm 的圆,作出直径CF,再分别以 F,C为圆心,以OF 为半径作弧,与⊙O相交于点A,E 和B,D,则A,B,C,D,E,F 是⊙O 的六等分点,顺次连接各个等分点即可.
正六边形 ABCDEF 即为所求作.
典例2 45° 解析:如图,连接OC,OD,OE,OQ,
∵正六边形 ABCDEF是⊙O的内接正六边形,
∴ ∠COD = ∠DOE =
∵点Q是DE的中点,∴∠DOQ = ∠EOQ =
∴∠COQ=∠COD+∠DOQ=60°+30°=90°,
变式 D
典例3 C
变式 D
典例4 B
变式 B
【当堂测·夯基础】
1. B 2. C
3. C 解析:如图,连接AC,交 EF 于点 M,则AC所在的直线是正三角形,正方形及圆的对称轴,
∴AC⊥EF,设半径为 r,则 EF=
在 Rt △AEM 中, ∠AEM=60°,
在 Rt△CMG中,∠MCG=45°,
同理 ∴GH=2CM=r,
4. A
5.方案二
解析:如图1中,圆的半径为3cm,∴底面积为9πcm .
如图2中,连接OA,OD.
∵OD=2 cm,∠OAD=30°,∠ADO=90°,∴OA=2OD=4 cm,
∴等边三角形的边长
∴底面积
∴等边三角形作为底面时,面积比较小,底面积为
两种方案底面积差为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 圆
8 正多边形和圆
列清单·划重点
知识点1 圆的内接正n边形
把⊙O分成n等份,顺次连接这 n个等分点,便得到了一个⊙O的内接 .
知识点2 正多边形的有关概念
1.正多边形的中心:一个正 n边形一共有n条对称轴,正多边形的对称轴相交于一点,这个点到正多边形各边的距离都相等,到正多边形各顶点的距离也都相等,这个点叫做 .
2.正多边形的外接圆:以正多边形的中心为圆心,以中心到一个顶点的距离为半径作圆,便得到这个正多边形的 .正多边形的外接圆的 叫做正多边形的半径.
3.正多边形的内切圆:以正多边形的中心为圆心,以中心到一条边的距离为半径作圆,便得到这个正多边形的 .正多边形的内切圆的半径叫做正多边形的 .
4.正多边形的中心角:正多边形每一条边所对外接圆的圆心角叫做正多边形的 .
知识点3 与正多边形有关的计算
计算正多边形的边长、半径、边心距、中心角、周长和面积之间的关系的问题时,通常归结为解三角形的问题.
如图所示,设正 n边形的半径为R,边心距为r,边长为a,半中心角为θ,周长为p,面积为S,则
(1)正n边形的中心角与它的每个外角相等,都等于
知识点4 用尺规作正多边形
1.正四边形、正八边形的作法
如图所示,在⊙O中,用直尺和圆规作两条 ,顺次连接这两条直径的四个端点,便得到一个正四边形.
如果再逐次平分各边所对的劣弧,那么就可以作出正八边形.如图所示.
2.正六边形、正三角形的作法
如图所示,先作⊙O的任意一条直径 AB,再分别以A,B为圆心,以 为半径作弧,与⊙O相交于点 C,D和E,F,则A,C,E,B,F,D是⊙O的六等分点,然后顺次连 接 各 等 点,即得 到 正 六 边 形ACEBFD,顺次连接B,C,D,即得到正三角形BCD.
明考点·识方法
考点1 正多边形的作图
典例1 用直尺和圆规作一个正八边形.
思路导析 作两条互相垂直的直径,将圆分成四条相等的弧,再将每条弧分别二等分,顺次连接八个等分点,所得到的八边形就是正八边形.
变式 画一个半径为2cm 的正六边形.
考点2 利用正多边形的性质求角的度数
典例2 如图,正六边形ABCDEF内接于⊙O,点P 在 上,点Q 是 的中点,则∠CPQ 的度数为 .
思路导析 根据圆内接正六边形中心角的计算方法求出∠COD=∠DOE=60°,再根据圆周角定理求出∠COQ的度数,再由圆周角定理进行计算即可.
变式 如图,用若干个全等的正五边形排成圆环状,图中所示的是其中 3 个正五边形的位置.要完成这一圆环排列,共需要正五边形的个数是( )
A.7个 B.8个 C.9个 D.10个
考点3 利用正多边形的性质求线段长
典例3 如图,已知⊙O的周长等于6π,则该圆内接正六边形ABCDEF 的 边 心 距OG 为 ( )
B. D.3
思路导析 连接OC,OD,由圆的周长可求出OC长,由正六边形 ABCDEF 可求出∠COD=60°,进而可求出∠COG=30°,根据30°角的锐角三角函数值即可求出边心距OG的长.
规律总结
圆内接正三角形的边长是它的半径的 倍,圆内接正方形的边长是它的半径的 倍,圆内接正六边形的边长等于它的半径.
变式 如图,等边三角形ABC和正方形DEFG 均内接于⊙O,若 EF=2,则 BC的长为 ( )
B.2 C. D.
考点4 利用正多边形的性质求面积
典例4 如图,⊙O的周长为 8π,正六边形 ABCDEF 内接于⊙O.则△OAB 的面积为( )
A.4 C.6
思路导析 根据正六边形的性质以及直角三角形的边角关系进行计算即可.
变式 剪纸艺术是我国的非物质文化遗产,如图是以正八边形为背景图形设计成的剪纸作品,记正八边形A B C D E F G H 的面积为 S .图中阴影部分面积 S ,则的值为 ( )
当堂测·夯基础
1.如图,画出了⊙O的内接正四边形和内接正五边形,且点 A在B,C之间,则 ∠ABC= ( )
A.6° B.9° C.12° D.18°
第1题图 第2题图
2.如图,电子屏幕上有边长为1 的正六边形 ABCDEF,红色光点和蓝色光点会按规则在六个顶点上闪亮.规则为:红点按顺时针方向每秒一个顶点依次闪亮(例如,经过1 秒由点A 亮变为点 F 亮),蓝点按逆时针方向每秒隔1个顶点闪亮(例如,经过1 秒由点A亮变为点 C 亮).若一开始,红点在 A处,蓝点在 B 处同时开始闪亮,则经过751秒后,两个闪亮的顶点之间的距离是( )
A.0 B.1 C. D.2
3.如图,正方形ABCD内接于⊙O,等边△AEF的顶点E,F分别在BC,CD上,EF交BC,CD于点G,H,则 的值等于( )
A. B. C. D.2
4.苯(分子式为C H )的环状结构是由德国化学家凯库勒提出的.随着研究的不断深入,发现苯分子中的6个碳原子组成了一个完美的正六边形(如图1),图2 是其平面示意图,点O为正六边形ABCDEF 的中心,则∠CBF-∠COD 的度数为 ( )
A.30° B.45° C.60° D.90°
5.某厂家要设计一个装彩铅的纸盒,已知每支笔形状、大小相同,底面均为正六边形,六边形的边长为1 cm,目前厂家提供了圆形和等边三角形两种作为底面的设计方案,我们以6支彩铅为例,可以设计如图收纳方案一和收纳方案二,你认为底面积更小的是 ,两种方案底面积差为 (结果保留根号).
参考答案
【列清单·划重点】
知识点1 正n边形
知识点2 1.正多边形的中心 2.外接圆半径 3.内切圆 边心距 4.中心角
知识点4 1.相互垂直的直径 2. OA
【明考点·识方法】
典例1 解:步骤如下:
(1)任意作一个圆,记作⊙O;
(2)用直尺作⊙O的一条直径AE;
(3)用直尺和圆规作 AE 的垂直平分线与⊙O交于C,G两点;
(4)用圆规将 AC,CE,EG,GA分别二等分,顺次连接上述八个等分点(如图所示).那么八边形ABCDEFGH 就是所要求作的正八边形.
变式 解:如图所示,作半径是2cm 的圆,作出直径CF,再分别以 F,C为圆心,以OF 为半径作弧,与⊙O相交于点A,E 和B,D,则A,B,C,D,E,F 是⊙O 的六等分点,顺次连接各个等分点即可.
正六边形 ABCDEF 即为所求作.
典例2 45° 解析:如图,连接OC,OD,OE,OQ,
∵正六边形 ABCDEF是⊙O的内接正六边形,
∴ ∠COD = ∠DOE =
∵点Q是DE的中点,∴∠DOQ = ∠EOQ =
∴∠COQ=∠COD+∠DOQ=60°+30°=90°,
变式 D
典例3 C
变式 D
典例4 B
变式 B
【当堂测·夯基础】
1. B 2. C
3. C 解析:如图,连接AC,交 EF 于点 M,则AC所在的直线是正三角形,正方形及圆的对称轴,
∴AC⊥EF,设半径为 r,则 EF=
在 Rt △AEM 中, ∠AEM=60°,
在 Rt△CMG中,∠MCG=45°,
同理 ∴GH=2CM=r,
4. A
5.方案二
解析:如图1中,圆的半径为3cm,∴底面积为9πcm .
如图2中,连接OA,OD.
∵OD=2 cm,∠OAD=30°,∠ADO=90°,∴OA=2OD=4 cm,
∴等边三角形的边长
∴底面积
∴等边三角形作为底面时,面积比较小,底面积为
两种方案底面积差为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
