人教版高中物理 选择性必修第三册 4.5 粒子的波动性(共27张PPT)
文档属性
| 名称 | 人教版高中物理 选择性必修第三册 4.5 粒子的波动性(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-03-02 18:18:40 | ||
图片预览





文档简介
(共27张PPT)
第四章 原子结构和波粒二象性
第 5节 粒子的波动性
学习目标
1. 知道一切实物粒子和光子一样都具有波粒二象性。
2. 知道德布罗意关系,会计算德布罗意波的波长
3.光的波动性是光子的固有属性
4.光波是一种概率波,德布罗意波也是概率波。
5. 了解不确定关系的概念。
6. 了解物理模型与物理现象。
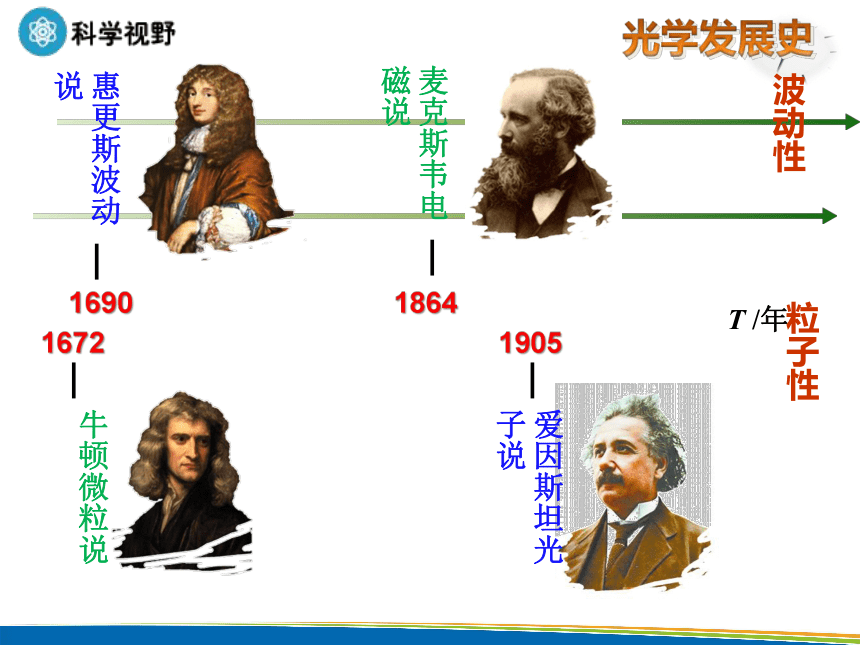
光学发展史
T /年
波动性
粒子性
1690
惠更斯波动说
1672
牛顿微粒说
1905
爱因斯坦光子说
1864
麦克斯韦电磁说
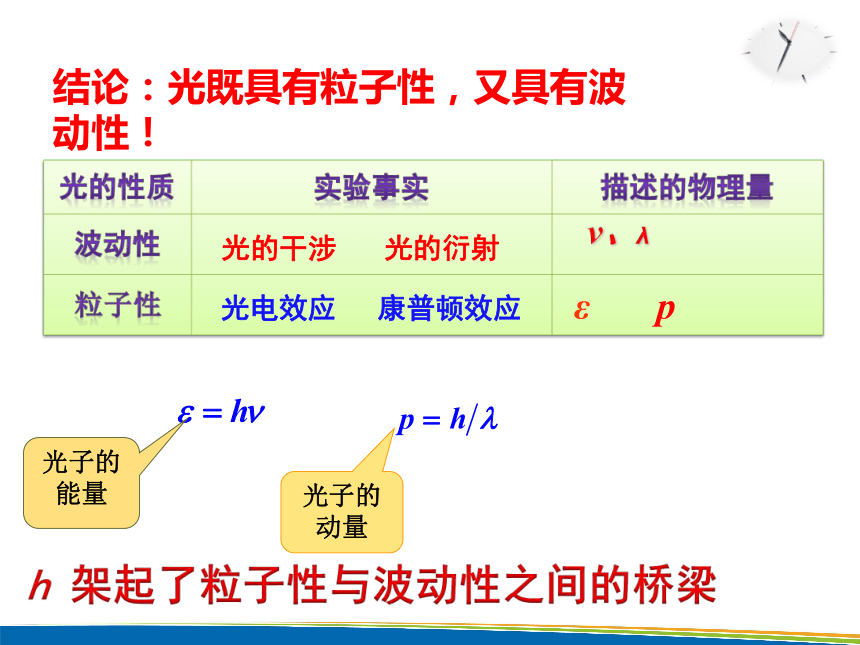
结论:光既具有粒子性,又具有波动性!
光的性质 实验事实 描述的物理量
波动性
粒子性
光的干涉
光的衍射
光电效应
康普顿效应
ν、λ
光子的能量
光子的动量
h 架起了粒子性与波动性之间的桥梁
ε p
学习提纲
1.1924年,法国物理学家德布罗意受到( )和( )理论的启发,大胆把光的波粒二象性推到实物粒子。
2.德布罗意类比的方法是:
3.德布罗意根据类比的方法提出假设( )
4德布罗意波长公式
5.德布罗意波的概念
普朗克能量子
爱因斯坦光子
在光学上与波动方面的研究相比,忽视了粒子方面研究,而在实物粒子的研究上,是否发生了相反的错误呢?我们是不是把粒子方面的图象想得太多而忽视了波的现象?”
实物粒子也具有波动性
这种和实物粒子相联系的波称为德布罗意波 ( 物质波),其波长 称为德布罗意波长。
电子动能 Ek = 100 eV.子弹动量 p = 6.63×106kg·m·s-1, 求德布罗意波长。h=6.63×10-34J.S
解:
如果你是德布罗意,将如何验证自己的观点
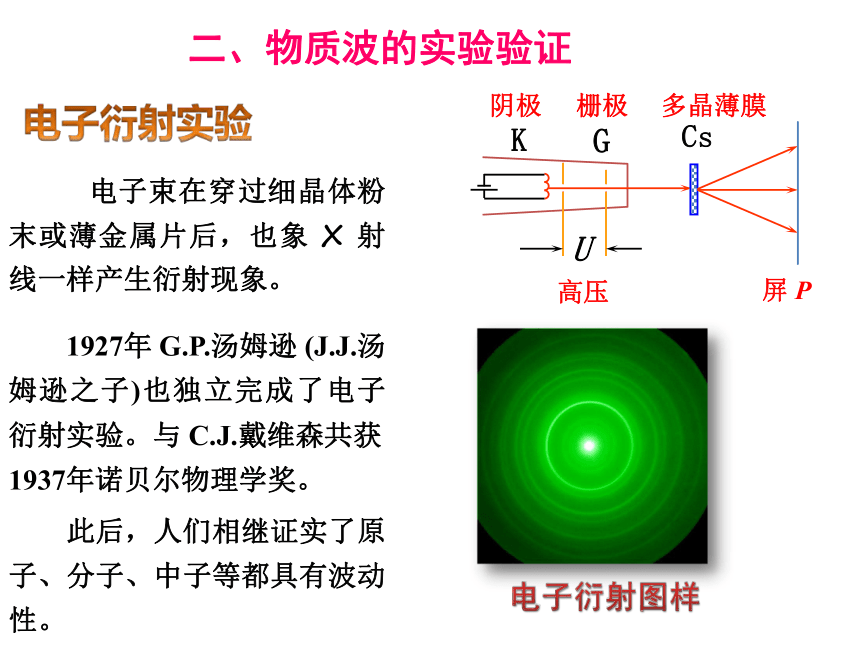
1927年 G.P.汤姆逊 (J.J.汤姆逊之子)也独立完成了电子衍射实验。与 C.J.戴维森共获 1937年诺贝尔物理学奖。
屏 P
多晶薄膜
高压
栅极
阴极
电子衍射实验
电子束在穿过细晶体粉末或薄金属片后,也象 X 射线一样产生衍射现象。
此后,人们相继证实了原子、分子、中子等都具有波动性。
电子衍射图样
二、物质波的实验验证
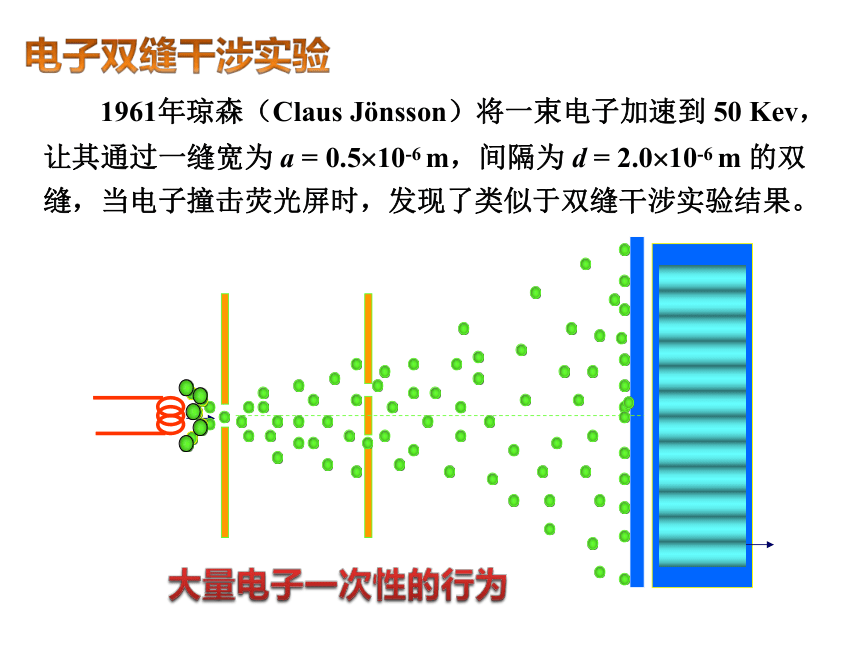
电子双缝干涉实验
1961年琼森(Claus J nsson)将一束电子加速到 50 Kev,让其通过一缝宽为 a = 0.5 10-6 m,间隔为 d = 2.0 10-6 m 的双缝,当电子撞击荧光屏时,发现了类似于双缝干涉实验结果。
大量电子一次性的行为
把光的波粒二象性的思想推广到微观粒子和任何运动着的物体上去,得出物质波(德布罗意波)的概念:任何一个运动着的物体都有一种波与它对应,该波的波长 λ = h/p
结论:
练习巩固
1.如果一个电子的德布罗意波长和一个中子的相等,则它们的( )也相等。
A。速度 B。动能 C。动量 D。总能量
2.电子束经实验得出了其衍射图样,从而证实了电子具有( )
C
波动性
第 4 节:概 率 波
第十七章:波粒二象性
经典的粒子经典的波(经典物理学关于粒子和波的概念)
经典的粒子:
具有空间大小、质量、电量等,遵从牛顿第二定律,任意
时刻有确定的位置和速度,以及确定的运动轨迹。
经典的波:
某种物理量呈时空周期性的分布 ( 确定的点处具有时间周期性,确定的方向上具有空间周期性),特征是具有频率和波长。
在经典物理学中,物质要么具有粒子性,要么具有波动性 .为什么微观粒子能够具这两种属性于一身呢
一、概率波
按照波动理论明纹处的光的强度大。按照光子理论明纹处到达的光子数多.
这是否可以认为,是光子之间的相互作用使它表现出了波动性,而不是光子本身就具有的属性呢?
光的双缝干涉实验
用非常弱的光子束进行双缝干涉
调弱光源的强度,让前一个光子到达屏幕后才发射第二个光子。开始光子打在屏幕上的位置是任意的,不可预知的。
随着时间推移,光子数目的增多光子出现稳定的分布
出现清晰干涉条纹和强光子束在短时间形成的一样
实验结论
光的波动性不是光子之间的相互作用引起的,而是光子自身固有的性质。
学习提纲
1.能不能准确预测单个光子的落点呢?为什么?
2.什么规律决定光子在空间分布的概率。
3.大量粒子( )导致确定的宏观结果
4.德国物理学家波恩的观点是什么?
5.光波是一种( )
德布罗意波也是一种 ( )
光子打在哪点是随机的,不确定的。没有固定的位置和轨道。
波动的规律
概率的分布
光子落在各点的概率是不一样的。光子落在明处的概率大,落在暗处的概率小
概率波
概率波
二.结论
光子在空间出现的概率可以通过波动的规律确定,所以从光子的概念上看,光波是一种概率波。德布罗意波也是概率波
2.下列关于光的波粒二象性的说法中,正确的是
( )
A. 有的光是波,有的光是粒子
B. 光子与电子是同样的一种粒子
C. 光的波长越长,其波动性越显著;波长越短,其粒子性越显著
D. 大量光子产生的效果往往显示粒子性
1.下列说法不正确的是 ( )
A. 光是一种电磁波
B. 光是一种概率波
C. 光子相当于高速运动的质点
D. 光的直线传播只是宏观近似规律
C
C
第 5 节:不确定性关系
第十七章:波粒二象性
根据经典物理学,如果我们已知一物体的初始位置和初始速度,就可以准确地确定以后任意时刻的位置和速度。
但是在微观世界中,由于微观粒子具有波动性,其坐标和动量不能同时确定。我们不能用经典的方法来描述它的粒子性,本节课我们就一起来学习。
光的单缝衍射
激光束
像屏
由于衍射,落点会超出单缝投影的范围,其它粒子也一样,说明微观粒子的运动已经不遵守牛顿运动定律,不能同时用粒子的位置和动量来描述粒子的运动了。
光的单缝衍射
讨 论
1. 在挡板左侧位置完全不确定
2. 在缝处位置不确定范围是缝宽 a = Δx
若减小缝宽:位置的不确定范围减小,但中央亮纹变宽,所以 x 方向动量的不确定量( Δpx )变大
入射粒子
x
y
O
a
θ
Δpx
3. 在缝后x方向有动量,也是不确定的
一、海森伯不确定关系
1927 年海森伯提出:粒子在某方向上的坐标不确定量与该方向上的动量不确定量的乘积必不小于普朗克常数。
1.微观粒子的坐标测得愈准确 ( x 0 ) ,动量就愈不准确 ( px ) ;
2.微观粒子的动量测得愈准确 ( px 0 ) ,坐标就愈不准确 ( x ) 。
但这里要注意,不确定关系
不是说微观粒子的坐标测不准;
也不是说微观粒子的动量测不准;
而是说微观粒子的坐标和动量不能同时测准。
不确定关系是物质的波粒二象性引起的。
对于微观粒子,我们不能用经典的物理学来描述。
海森伯的不确定关系说明
宏观物体 微观粒子
具有确定的坐标和动量,可用牛顿力学描述 没有确定的坐标和动量,需用量子力学描述
有连续可测的运动轨道,可追踪各个物体的运动轨迹 有概率分布特性,不可能分辨出各个粒子的轨迹
体系能量可以为任意的、连续变化的数值 能量量子化
二.物理模型和物理现象
练习
从衍射的规律可以知道,狭缝越窄,屏上中央亮条纹就越宽,有不确定性关系式 判断下列说法正确的是( )
A.入射的粒子有确定动量,射到屏上粒子就有准确的位置.
B.狭缝的宽度变小了,因此粒子的不确定性也变小了.
C.更窄的狭缝可以更准确地测得粒子的位置.但粒子动量的不确定性却更大了.
D.可以同时确定粒子的位置和动量
C
3.光的波动性是光子的固有属性
4.光波是一种概率波,德布罗意波也是概率波。
1.德布罗意的物质波,会计算德布罗意波的波长
2.知道一切实物粒子和光子一样都具有波粒二象性。
6. 了解物理模型与物理现象。
5. 海森伯不确定关系:
第四章 原子结构和波粒二象性
第 5节 粒子的波动性
学习目标
1. 知道一切实物粒子和光子一样都具有波粒二象性。
2. 知道德布罗意关系,会计算德布罗意波的波长
3.光的波动性是光子的固有属性
4.光波是一种概率波,德布罗意波也是概率波。
5. 了解不确定关系的概念。
6. 了解物理模型与物理现象。
光学发展史
T /年
波动性
粒子性
1690
惠更斯波动说
1672
牛顿微粒说
1905
爱因斯坦光子说
1864
麦克斯韦电磁说
结论:光既具有粒子性,又具有波动性!
光的性质 实验事实 描述的物理量
波动性
粒子性
光的干涉
光的衍射
光电效应
康普顿效应
ν、λ
光子的能量
光子的动量
h 架起了粒子性与波动性之间的桥梁
ε p
学习提纲
1.1924年,法国物理学家德布罗意受到( )和( )理论的启发,大胆把光的波粒二象性推到实物粒子。
2.德布罗意类比的方法是:
3.德布罗意根据类比的方法提出假设( )
4德布罗意波长公式
5.德布罗意波的概念
普朗克能量子
爱因斯坦光子
在光学上与波动方面的研究相比,忽视了粒子方面研究,而在实物粒子的研究上,是否发生了相反的错误呢?我们是不是把粒子方面的图象想得太多而忽视了波的现象?”
实物粒子也具有波动性
这种和实物粒子相联系的波称为德布罗意波 ( 物质波),其波长 称为德布罗意波长。
电子动能 Ek = 100 eV.子弹动量 p = 6.63×106kg·m·s-1, 求德布罗意波长。h=6.63×10-34J.S
解:
如果你是德布罗意,将如何验证自己的观点
1927年 G.P.汤姆逊 (J.J.汤姆逊之子)也独立完成了电子衍射实验。与 C.J.戴维森共获 1937年诺贝尔物理学奖。
屏 P
多晶薄膜
高压
栅极
阴极
电子衍射实验
电子束在穿过细晶体粉末或薄金属片后,也象 X 射线一样产生衍射现象。
此后,人们相继证实了原子、分子、中子等都具有波动性。
电子衍射图样
二、物质波的实验验证
电子双缝干涉实验
1961年琼森(Claus J nsson)将一束电子加速到 50 Kev,让其通过一缝宽为 a = 0.5 10-6 m,间隔为 d = 2.0 10-6 m 的双缝,当电子撞击荧光屏时,发现了类似于双缝干涉实验结果。
大量电子一次性的行为
把光的波粒二象性的思想推广到微观粒子和任何运动着的物体上去,得出物质波(德布罗意波)的概念:任何一个运动着的物体都有一种波与它对应,该波的波长 λ = h/p
结论:
练习巩固
1.如果一个电子的德布罗意波长和一个中子的相等,则它们的( )也相等。
A。速度 B。动能 C。动量 D。总能量
2.电子束经实验得出了其衍射图样,从而证实了电子具有( )
C
波动性
第 4 节:概 率 波
第十七章:波粒二象性
经典的粒子经典的波(经典物理学关于粒子和波的概念)
经典的粒子:
具有空间大小、质量、电量等,遵从牛顿第二定律,任意
时刻有确定的位置和速度,以及确定的运动轨迹。
经典的波:
某种物理量呈时空周期性的分布 ( 确定的点处具有时间周期性,确定的方向上具有空间周期性),特征是具有频率和波长。
在经典物理学中,物质要么具有粒子性,要么具有波动性 .为什么微观粒子能够具这两种属性于一身呢
一、概率波
按照波动理论明纹处的光的强度大。按照光子理论明纹处到达的光子数多.
这是否可以认为,是光子之间的相互作用使它表现出了波动性,而不是光子本身就具有的属性呢?
光的双缝干涉实验
用非常弱的光子束进行双缝干涉
调弱光源的强度,让前一个光子到达屏幕后才发射第二个光子。开始光子打在屏幕上的位置是任意的,不可预知的。
随着时间推移,光子数目的增多光子出现稳定的分布
出现清晰干涉条纹和强光子束在短时间形成的一样
实验结论
光的波动性不是光子之间的相互作用引起的,而是光子自身固有的性质。
学习提纲
1.能不能准确预测单个光子的落点呢?为什么?
2.什么规律决定光子在空间分布的概率。
3.大量粒子( )导致确定的宏观结果
4.德国物理学家波恩的观点是什么?
5.光波是一种( )
德布罗意波也是一种 ( )
光子打在哪点是随机的,不确定的。没有固定的位置和轨道。
波动的规律
概率的分布
光子落在各点的概率是不一样的。光子落在明处的概率大,落在暗处的概率小
概率波
概率波
二.结论
光子在空间出现的概率可以通过波动的规律确定,所以从光子的概念上看,光波是一种概率波。德布罗意波也是概率波
2.下列关于光的波粒二象性的说法中,正确的是
( )
A. 有的光是波,有的光是粒子
B. 光子与电子是同样的一种粒子
C. 光的波长越长,其波动性越显著;波长越短,其粒子性越显著
D. 大量光子产生的效果往往显示粒子性
1.下列说法不正确的是 ( )
A. 光是一种电磁波
B. 光是一种概率波
C. 光子相当于高速运动的质点
D. 光的直线传播只是宏观近似规律
C
C
第 5 节:不确定性关系
第十七章:波粒二象性
根据经典物理学,如果我们已知一物体的初始位置和初始速度,就可以准确地确定以后任意时刻的位置和速度。
但是在微观世界中,由于微观粒子具有波动性,其坐标和动量不能同时确定。我们不能用经典的方法来描述它的粒子性,本节课我们就一起来学习。
光的单缝衍射
激光束
像屏
由于衍射,落点会超出单缝投影的范围,其它粒子也一样,说明微观粒子的运动已经不遵守牛顿运动定律,不能同时用粒子的位置和动量来描述粒子的运动了。
光的单缝衍射
讨 论
1. 在挡板左侧位置完全不确定
2. 在缝处位置不确定范围是缝宽 a = Δx
若减小缝宽:位置的不确定范围减小,但中央亮纹变宽,所以 x 方向动量的不确定量( Δpx )变大
入射粒子
x
y
O
a
θ
Δpx
3. 在缝后x方向有动量,也是不确定的
一、海森伯不确定关系
1927 年海森伯提出:粒子在某方向上的坐标不确定量与该方向上的动量不确定量的乘积必不小于普朗克常数。
1.微观粒子的坐标测得愈准确 ( x 0 ) ,动量就愈不准确 ( px ) ;
2.微观粒子的动量测得愈准确 ( px 0 ) ,坐标就愈不准确 ( x ) 。
但这里要注意,不确定关系
不是说微观粒子的坐标测不准;
也不是说微观粒子的动量测不准;
而是说微观粒子的坐标和动量不能同时测准。
不确定关系是物质的波粒二象性引起的。
对于微观粒子,我们不能用经典的物理学来描述。
海森伯的不确定关系说明
宏观物体 微观粒子
具有确定的坐标和动量,可用牛顿力学描述 没有确定的坐标和动量,需用量子力学描述
有连续可测的运动轨道,可追踪各个物体的运动轨迹 有概率分布特性,不可能分辨出各个粒子的轨迹
体系能量可以为任意的、连续变化的数值 能量量子化
二.物理模型和物理现象
练习
从衍射的规律可以知道,狭缝越窄,屏上中央亮条纹就越宽,有不确定性关系式 判断下列说法正确的是( )
A.入射的粒子有确定动量,射到屏上粒子就有准确的位置.
B.狭缝的宽度变小了,因此粒子的不确定性也变小了.
C.更窄的狭缝可以更准确地测得粒子的位置.但粒子动量的不确定性却更大了.
D.可以同时确定粒子的位置和动量
C
3.光的波动性是光子的固有属性
4.光波是一种概率波,德布罗意波也是概率波。
1.德布罗意的物质波,会计算德布罗意波的波长
2.知道一切实物粒子和光子一样都具有波粒二象性。
6. 了解物理模型与物理现象。
5. 海森伯不确定关系:
同课章节目录
- 第一章 分子动理论
- 1 分子动理论的基本内容
- 2 实验:用油膜法估测油酸分子的大小
- 3 分子运动速率分布规律
- 4 分子动能和分子势能
- 第二章 气体、固体和液体
- 1 温度和温标
- 2 气体的等温变化
- 3 气体的等压变化和等容变化
- 4 固体
- 5 液体
- 第三章 热力学定律
- 1 功、热和内能的改变
- 2 热力学第一定律
- 3 能量守恒定律
- 4 热力学第二定律
- 第四章 原子结构和波粒二象性
- 1 普朗克黑体辐射理论
- 2 光电效应
- 3 原子的核式结构模型
- 4 氢原子光谱和玻尔的原子模型
- 5 粒子的波动性和量子力学的建立
- 第五章 原子核
- 1 原子核的组成
- 2 放射性元素的衰变
- 3 核力与结合能
- 4 核裂变与核聚变
- 5 “基本”粒子
