圆的确定课件
图片预览







文档简介
课件23张PPT。27.1 圆的确定 九年级数学(下)问题:
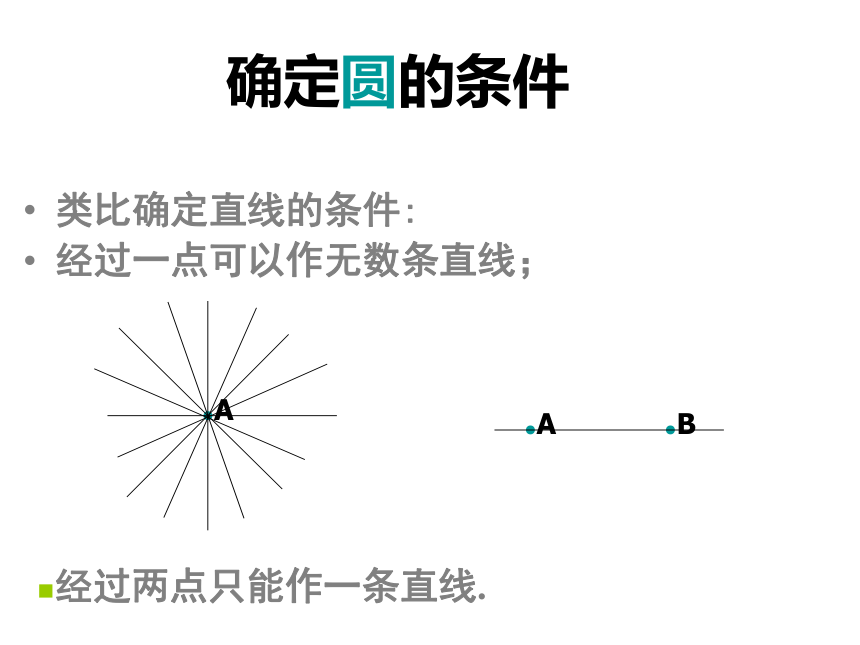
车间工人要将一个如图所示的破损的圆盘复原,你有办法吗?生活生产中的启示 想一想你能解决吗?确定圆的条件类比确定直线的条件:经过一点可以作无数条直线;经过两点只能作一条直线.●A●A●B确定圆的条件想一想,经过一点可以作几个圆?经过两点,三点,…,呢?1.作圆,使它过已知点A.你能作出几个这样的圆?●A2.作圆,使它过已知点A,B.你能作出几个这样的圆?●A●B确定圆的条件2. 过已知点A,B作圆,可以作无数个圆.经过两点A,B的圆的圆心在线段AB的垂直平分线上.
以线段AB的垂直平分线上的任意一点为圆心,这点到A或B的距离为半径作圆.你准备如何(确定圆心,半径)作圆?其圆心的分布有什么特点?与线段AB有什么关系?●A●B确定圆的条件3.作圆,使它过已知点A,B,C(A,B,C三点不在同一条直线上),你能作出几个这样的圆?老师提示:
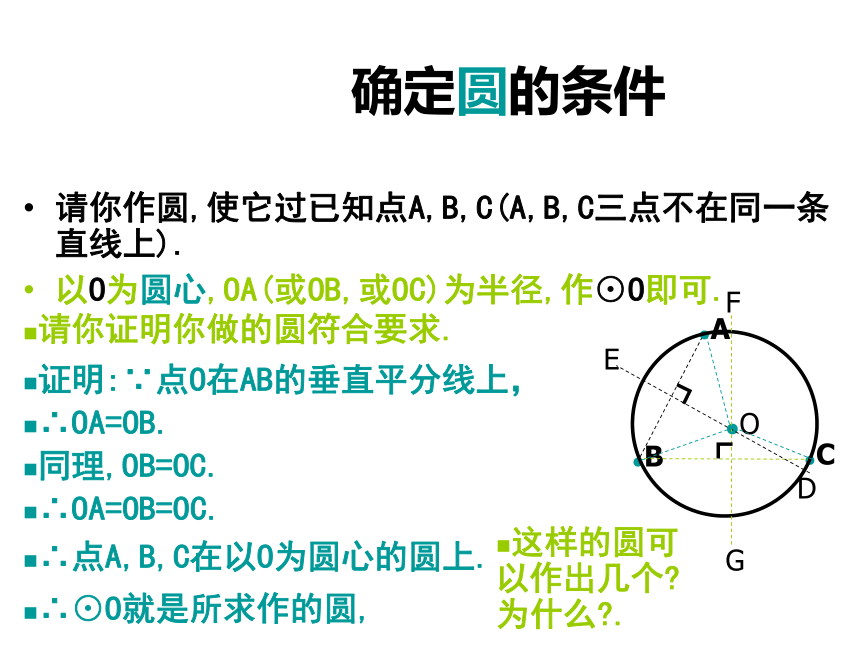
能否转化为2的情况:经过两点A,B的圆的圆心在线段AB的垂直平分线上. 你准备如何(确定圆心,半径)作圆?其圆心的位置有什么特点?与A,B,C有什么关系?●B●C经过两点B,C的圆的圆心在线段BC的垂直平分线上.●A经过三点A,B,C的圆的圆心应该在这两条垂直平分线的交点O的位置.●O确定圆的条件请你作圆,使它过已知点A,B,C(A,B,C三点不在同一条直线上).以O为圆心,OA(或OB,或OC)为半径,作⊙O即可.请你证明你做的圆符合要求.●B●C●A●O证明:∵点O在AB的垂直平分线上,∴⊙O就是所求作的圆,∴OA=OB.同理,OB=OC.∴OA=OB=OC.∴点A,B,C在以O为圆心的圆上.这样的圆可以作出几个?为什么?.三点定圆定理 不在一条直线上的三个点确定一个圆.在上面的作图过程中.老师期望:
将这个结论及其证明作为一种模型对待.∵直线DE和FG只有一个交点O,并且点O到A,B,C三个点的距离相等,∴经过点A,B,C三点可以作一个圆,并且只能作一个圆.三角形与圆的位置关系因此,三角形的三个顶点确定一个圆,这圆叫做三角形的外接圆.这个三角形叫做圆的内接三角形.外接圆的圆心是三角形三边垂直平分线的的交点,叫做三角形的外心.老师提示:
多边形的顶点与圆的位置关系称为接.三角形与圆的位置关系分别作出锐角三角形,直角三角形,钝角三角形的外接圆,并说明与它们外心的位置情况锐角三角形的外心位于三角形内,直角三角形的外心位于直角三角形斜边中点,钝角三角形的外心位于三角形外.老师期望:
作三角形的外接圆是必备基本技能,定要熟练掌握. 现在你知道了怎样要将一个如图所示的破损的圆盘复原了吗?小故事: 中国古代有一个叫《路边苦李》的故事:王戎7岁时,与小伙伴们外出游玩,看到路边的李树上结满了果子.小伙伴们纷纷去摘取果子,只有王戎站在原地不动.有人问王戎为什么?王戎回答说:“树在道边而多子,此必苦李.”
小伙伴摘取一个尝了一下果然是苦李. 王戎是怎样知道李子是苦的吗?他运用了怎样的推理方法?反证法先假设命题不成立,
从这样的假设出发,经过推理得出和已知条件矛盾,或者与定义,公理,定理等矛盾,
从而得出假设命题不成立,是错误的,
即所求证的命题正确.在证明一个命题时,人们有时反证法定义:这种证明方法叫做反证法.试一试∴∠1=∠2 (两直线平行,同位角相等)这与已知的∠1≠∠2矛盾∴假设不成立证明:假设结论不成立,则a∥b例:求证:在同一平面内,如果一条直线和两条平行直线中的一条相交,那么和另一条也相交.已知:直线l1,l2,l3在同一平面内,且l1∥l2,l3与l1相交于点P.求证:l3与l2相交.证明:假设____________,那么_________.因为已知_________,这与“_______________________ _____________”矛盾.所以假设不成立,即求证的命题正确.l3与l2 不相交.l3∥l2l1∥l2 经过直线外一点,有且只有一条直线平行于已知直线所以过直线l2外一点P,有两条直线和l2平行,练一练 用反证法证明(填空):在三角形的内角中,至少有一个角大于或等于60°.这与________________________________相矛盾.所以______不成立,所求证的结论成立. 已知: ∠A,∠B,∠C是△ABC的内角. 求证: ∠A,∠B,∠C中至少有一个角大 于
或等于60°.证明: 假设所求证的结论不成立,即
∠A ___ 60° ,∠B ___ 60° ,∠C ___60°
则∠A+∠B+∠C < 180°.<<<三角形三个内角的和等于180°假设合作学习:求证:在同一平面内,如果两条直线都和第三条直线平行,那么这两条直线也互相平行.(1)你首先会选择哪一种证明方法?(2)如果选择反证法,先怎样假设?结果和什么产生矛盾?定理已知:如图,l1∥l2 ,l 2 ∥l 3求证: l1∥l3 ∵l1∥l2 , l2∥l3, 则过点p就有两条直线l1、 l3都与l2平行,这与“经过直线外一点,有且只有一条直线平行于已知直线”矛盾.证明:假设l1不平行l3,则l1与l3相交,设交点为p.p所以假设不成立,所求证的结论成立,即 l1∥l3 合作学习:求证:在同一平面内,如果两条直线都和第三条直线平行,那么这两条直线也互相平行.定理(3)不用反证法证明已知:如图,l1∥l2 ,l 2 ∥l 3求证: l1∥l3 lp∵l1∥l2 ,l 2∥l 3
∴直线l必定与直线l2,l3相交(在同一平面内,
如果一条直线和两条平行直线中的一条相
交,那么和另一条直线也相交)证明:作直线l交直线l2于点p,∴∠2 =∠1=∠3(两直线平行,同位角相等)∴ l1∥l3 (同位角相等,两直线平行)已知:如图,直线l与l1,l2,l3都相交,且 l1∥l3,l2∥l3,
求证:∠1=∠2练一练l1l2l3l⌒⌒12证明: ∵l1∥l3,l2∥l3(已知)
∴l1∥l2
(在同一平面内,如果两条直线
都和第三条直线平行,那么这
两条直线也互相平行)
∴∠1=∠2(两直线平行,同位角相等)[能力测试]写出下列各结论的反面:
(1)a//b;
(2)a≥0;
(3)b是正数;
(4)a⊥ba<0b是0或负数a不垂直于b变式训练1、“a<b”的反面应是( )
(A)a≠>b (B)a >b
(C)a=b (D)a=b或a >b2、用反证法证明命题“三角形中最多有一个是直角”时,应如何假设?
___________________________________D假设三角形中有两个或三个角是直角总结回顾:2、反证法的一般步骤:从假设出发1、反证法的概念;假设命题不成立引出矛盾假设不成立求证的命题正确得出结论假设归谬结论结束寄语盛年不重来,一日难再晨,及时宜自勉,岁月不待人.再见
车间工人要将一个如图所示的破损的圆盘复原,你有办法吗?生活生产中的启示 想一想你能解决吗?确定圆的条件类比确定直线的条件:经过一点可以作无数条直线;经过两点只能作一条直线.●A●A●B确定圆的条件想一想,经过一点可以作几个圆?经过两点,三点,…,呢?1.作圆,使它过已知点A.你能作出几个这样的圆?●A2.作圆,使它过已知点A,B.你能作出几个这样的圆?●A●B确定圆的条件2. 过已知点A,B作圆,可以作无数个圆.经过两点A,B的圆的圆心在线段AB的垂直平分线上.
以线段AB的垂直平分线上的任意一点为圆心,这点到A或B的距离为半径作圆.你准备如何(确定圆心,半径)作圆?其圆心的分布有什么特点?与线段AB有什么关系?●A●B确定圆的条件3.作圆,使它过已知点A,B,C(A,B,C三点不在同一条直线上),你能作出几个这样的圆?老师提示:
能否转化为2的情况:经过两点A,B的圆的圆心在线段AB的垂直平分线上. 你准备如何(确定圆心,半径)作圆?其圆心的位置有什么特点?与A,B,C有什么关系?●B●C经过两点B,C的圆的圆心在线段BC的垂直平分线上.●A经过三点A,B,C的圆的圆心应该在这两条垂直平分线的交点O的位置.●O确定圆的条件请你作圆,使它过已知点A,B,C(A,B,C三点不在同一条直线上).以O为圆心,OA(或OB,或OC)为半径,作⊙O即可.请你证明你做的圆符合要求.●B●C●A●O证明:∵点O在AB的垂直平分线上,∴⊙O就是所求作的圆,∴OA=OB.同理,OB=OC.∴OA=OB=OC.∴点A,B,C在以O为圆心的圆上.这样的圆可以作出几个?为什么?.三点定圆定理 不在一条直线上的三个点确定一个圆.在上面的作图过程中.老师期望:
将这个结论及其证明作为一种模型对待.∵直线DE和FG只有一个交点O,并且点O到A,B,C三个点的距离相等,∴经过点A,B,C三点可以作一个圆,并且只能作一个圆.三角形与圆的位置关系因此,三角形的三个顶点确定一个圆,这圆叫做三角形的外接圆.这个三角形叫做圆的内接三角形.外接圆的圆心是三角形三边垂直平分线的的交点,叫做三角形的外心.老师提示:
多边形的顶点与圆的位置关系称为接.三角形与圆的位置关系分别作出锐角三角形,直角三角形,钝角三角形的外接圆,并说明与它们外心的位置情况锐角三角形的外心位于三角形内,直角三角形的外心位于直角三角形斜边中点,钝角三角形的外心位于三角形外.老师期望:
作三角形的外接圆是必备基本技能,定要熟练掌握. 现在你知道了怎样要将一个如图所示的破损的圆盘复原了吗?小故事: 中国古代有一个叫《路边苦李》的故事:王戎7岁时,与小伙伴们外出游玩,看到路边的李树上结满了果子.小伙伴们纷纷去摘取果子,只有王戎站在原地不动.有人问王戎为什么?王戎回答说:“树在道边而多子,此必苦李.”
小伙伴摘取一个尝了一下果然是苦李. 王戎是怎样知道李子是苦的吗?他运用了怎样的推理方法?反证法先假设命题不成立,
从这样的假设出发,经过推理得出和已知条件矛盾,或者与定义,公理,定理等矛盾,
从而得出假设命题不成立,是错误的,
即所求证的命题正确.在证明一个命题时,人们有时反证法定义:这种证明方法叫做反证法.试一试∴∠1=∠2 (两直线平行,同位角相等)这与已知的∠1≠∠2矛盾∴假设不成立证明:假设结论不成立,则a∥b例:求证:在同一平面内,如果一条直线和两条平行直线中的一条相交,那么和另一条也相交.已知:直线l1,l2,l3在同一平面内,且l1∥l2,l3与l1相交于点P.求证:l3与l2相交.证明:假设____________,那么_________.因为已知_________,这与“_______________________ _____________”矛盾.所以假设不成立,即求证的命题正确.l3与l2 不相交.l3∥l2l1∥l2 经过直线外一点,有且只有一条直线平行于已知直线所以过直线l2外一点P,有两条直线和l2平行,练一练 用反证法证明(填空):在三角形的内角中,至少有一个角大于或等于60°.这与________________________________相矛盾.所以______不成立,所求证的结论成立. 已知: ∠A,∠B,∠C是△ABC的内角. 求证: ∠A,∠B,∠C中至少有一个角大 于
或等于60°.证明: 假设所求证的结论不成立,即
∠A ___ 60° ,∠B ___ 60° ,∠C ___60°
则∠A+∠B+∠C < 180°.<<<三角形三个内角的和等于180°假设合作学习:求证:在同一平面内,如果两条直线都和第三条直线平行,那么这两条直线也互相平行.(1)你首先会选择哪一种证明方法?(2)如果选择反证法,先怎样假设?结果和什么产生矛盾?定理已知:如图,l1∥l2 ,l 2 ∥l 3求证: l1∥l3 ∵l1∥l2 , l2∥l3, 则过点p就有两条直线l1、 l3都与l2平行,这与“经过直线外一点,有且只有一条直线平行于已知直线”矛盾.证明:假设l1不平行l3,则l1与l3相交,设交点为p.p所以假设不成立,所求证的结论成立,即 l1∥l3 合作学习:求证:在同一平面内,如果两条直线都和第三条直线平行,那么这两条直线也互相平行.定理(3)不用反证法证明已知:如图,l1∥l2 ,l 2 ∥l 3求证: l1∥l3 lp∵l1∥l2 ,l 2∥l 3
∴直线l必定与直线l2,l3相交(在同一平面内,
如果一条直线和两条平行直线中的一条相
交,那么和另一条直线也相交)证明:作直线l交直线l2于点p,∴∠2 =∠1=∠3(两直线平行,同位角相等)∴ l1∥l3 (同位角相等,两直线平行)已知:如图,直线l与l1,l2,l3都相交,且 l1∥l3,l2∥l3,
求证:∠1=∠2练一练l1l2l3l⌒⌒12证明: ∵l1∥l3,l2∥l3(已知)
∴l1∥l2
(在同一平面内,如果两条直线
都和第三条直线平行,那么这
两条直线也互相平行)
∴∠1=∠2(两直线平行,同位角相等)[能力测试]写出下列各结论的反面:
(1)a//b;
(2)a≥0;
(3)b是正数;
(4)a⊥ba<0b是0或负数a不垂直于b变式训练1、“a<b”的反面应是( )
(A)a≠>b (B)a >b
(C)a=b (D)a=b或a >b2、用反证法证明命题“三角形中最多有一个是直角”时,应如何假设?
___________________________________D假设三角形中有两个或三个角是直角总结回顾:2、反证法的一般步骤:从假设出发1、反证法的概念;假设命题不成立引出矛盾假设不成立求证的命题正确得出结论假设归谬结论结束寄语盛年不重来,一日难再晨,及时宜自勉,岁月不待人.再见
