2025年中考数学二轮复习专题全等三角形之倍长中线法 课件(共26张PPT)
文档属性
| 名称 | 2025年中考数学二轮复习专题全等三角形之倍长中线法 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 623.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-03 05:50:32 | ||
图片预览



文档简介
(共26张PPT)
2025年中考数学二轮复习专题
全等三角形之倍长中线法
当线段出现一个中点时,特别是三角形中,常常采用“倍长中线法”添加辅助线.倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.倍长中线法:△ABC中AD是BC边中线
方式1: 延长AD到E, 使DE=AD,连接BE
倍长中线法
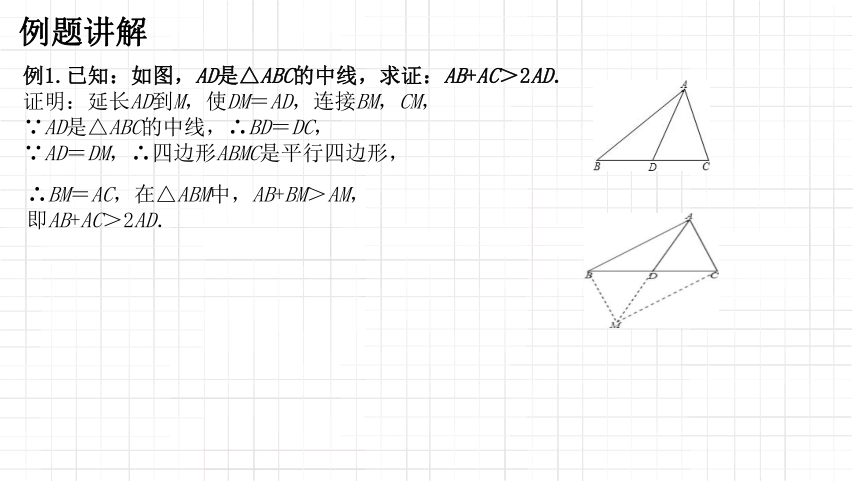
例1.已知:如图,AD是△ABC的中线,求证:AB+AC>2AD.
证明:延长AD到M,使DM=AD,连接BM,CM,
∵AD是△ABC的中线,∴BD=DC,
∵AD=DM,∴四边形ABMC是平行四边形,
∴BM=AC,在△ABM中,AB+BM>AM,
即AB+AC>2AD.
例题讲解
例2.已知,如图△ABC中,AB=5,AC=3,则中线AD的取值范围是 .
解:延长AD到点E,使AD=ED,连接CE,∵AD是△ABC的中线,
∴BD=CD,在△ABD和△ECD中
∴△ABD≌△ECD(SAS),∴AB=EC,在△AEC中,AC+EC>AE,
且EC﹣AC<AE,即AB+AC>2AD,AB﹣AC<2AD,
∴2<2AD<8,∴1<AD<4,
故答案为:1<AD<4.
例题讲解
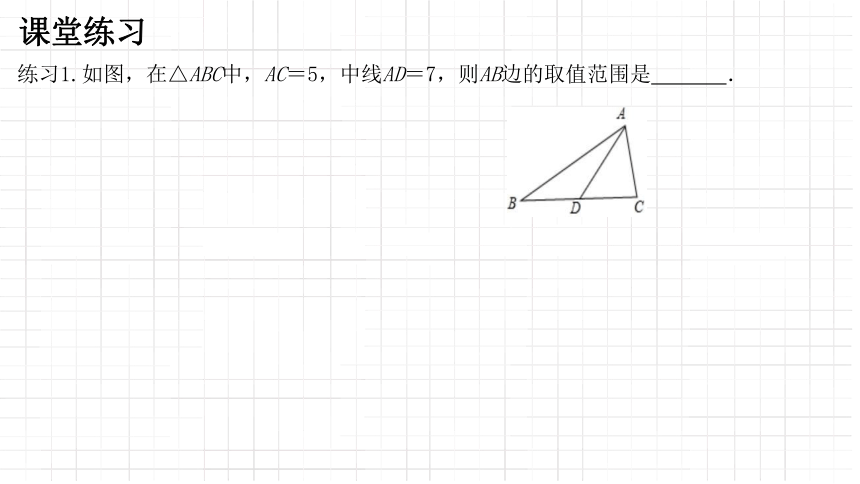
练习1.如图,在△ABC中,AC=5,中线AD=7,则AB边的取值范围是 .
课堂练习
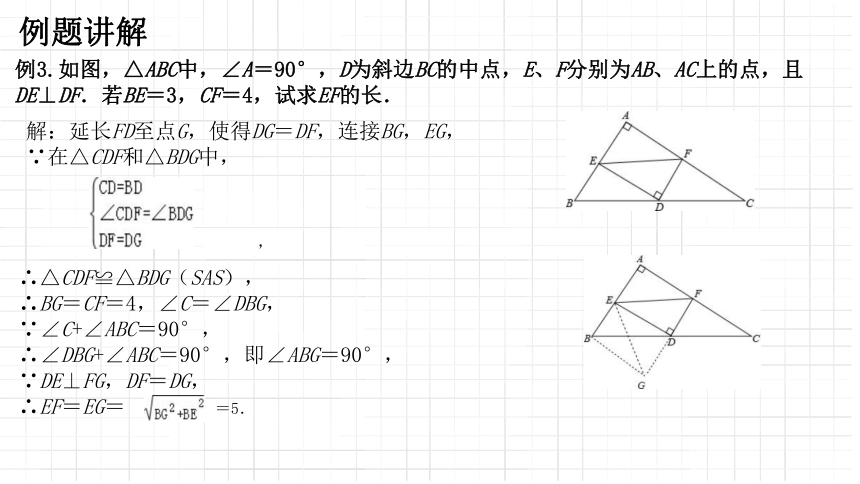
例3.如图,△ABC中,∠A=90°,D为斜边BC的中点,E、F分别为AB、AC上的点,且DE⊥DF.若BE=3,CF=4,试求EF的长.
解:延长FD至点G,使得DG=DF,连接BG,EG,
∵在△CDF和△BDG中,
,
∴△CDF≌△BDG(SAS),
∴BG=CF=4,∠C=∠DBG,
∵∠C+∠ABC=90°,
∴∠DBG+∠ABC=90°,即∠ABG=90°,
∵DE⊥FG,DF=DG,
∴EF=EG=
=5.
例题讲解
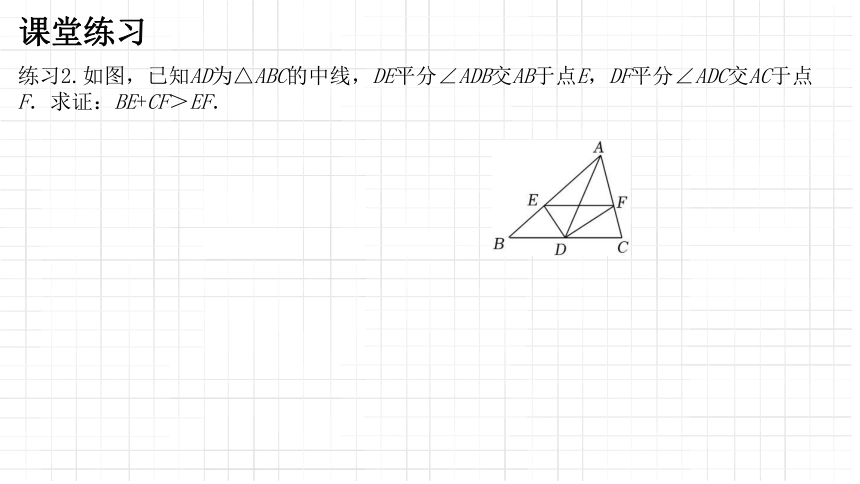
练习2.如图,已知AD为△ABC的中线,DE平分∠ADB交AB于点E,DF平分∠ADC交AC于点F.求证:BE+CF>EF.
课堂练习
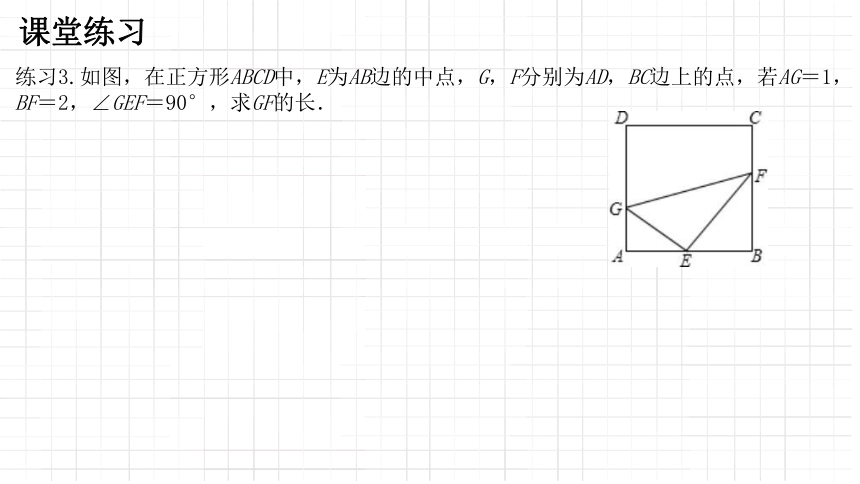
练习3.如图,在正方形ABCD中,E为AB边的中点,G,F分别为AD,BC边上的点,若AG=1,BF=2,∠GEF=90°,求GF的长.
课堂练习
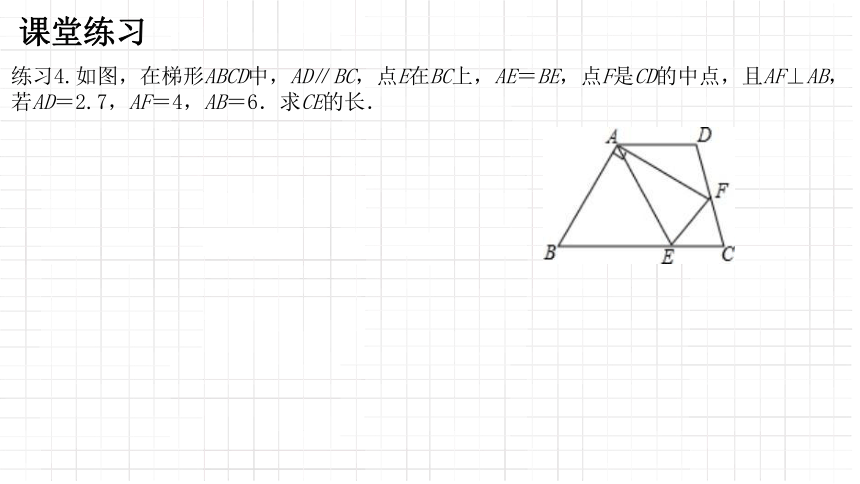
练习4.如图,在梯形ABCD中,AD∥BC,点E在BC上,AE=BE,点F是CD的中点,且AF⊥AB,若AD=2.7,AF=4,AB=6.求CE的长.
课堂练习
例4.如图,在△ABC中,AB=AC,E是AB中点,延长AB到D,使BD=BA,延长CE至F,使得EF=CE.求证:CD=2CE.
证明:∵点E为AB的中点,∴BE=AE,
在△BEF和△AEC中,
∴△BEF≌△AEC(SAS),∴BF=AC,∠EBF=∠A,
∵AB=AC=BD,∴∠ACB=∠ABC,BF=BD,
∵∠CBD=∠A+∠ACB,∠CBF=∠ABC+∠EBF,∴∠CBD=∠CBF,
在△CBD和△CBF中,
∴△CBD≌△CBF(SAS),
∴CD=CF,∵CF=CE+EF,CE=EF,∴CF=2CE,∴CD=2CE.
例题讲解
练习5.已知:如图,在△ABC中,AB=AC,延长AB到D,使BD=AB,E为AB的中点.
求证:CD=2CE
课堂练习
练习6.已知CD=AB,∠BDA=∠BAD,AE是△ABD的中线,
求证:∠C=∠BAE.
课堂练习
练习7.如图,已知D是△ABC的边BC上的一点,CD=AB,∠BDA=∠BAD,AE是△ABD的中线.求证:AD是∠EAC的平分线.
课堂练习
例5.如图,在△ABC中,AD平分∠BAC,E为BC的中点,过点E作EF∥AD交AB于点G,交CA的延长线于点F.求证:BG=CF.
证明:作CM∥AB交FE的延长线于M.∵BG∥CM,
∴∠B=∠MCE,∵E是BC中点,
∴BE=EC,在△BEG和△CEM中,
∴△BEG≌△CEM,∴BG=CM,∵AD∥EF
∴∠1=∠FGA,
∠2=∠F,∵∠1=∠2,∴∠F=∠FGA,∵AB∥CM,
∴∠FGA=∠M,∴∠F=∠M,∴CF=CM,
∴BG=CF.
例题讲解
练习8.已知:如图,△ABC(AB≠AC)中,D、E在BC上,且DE=EC,过D作DF∥BA交AE于点F,DF=AC.求证:AE平分∠BAC.
课堂练习
例6.已知在△ABC中,AD是BC边上的中线,分别以AB边、AC边为直角边各向外作等腰直角三角形,如图,求证:EF=2AD.
证明:延长AD至点G,使得AD=DG,连接BG,CG,
∵AD=DG,BD=CD,∴四边形ABGC是平行四边形,
∴AC=AF=BG,AB=AE=CG,∠BAC+∠ABG=180°,
∵∠EAF+∠BAC=180°,∴∠EAF=∠ABG,
在△EAF和△BAG中,
∴△EAF≌△BAG(SAS)
∴EF=AG,
∵AG=2AD,
∴EF=2AD.
例题讲解
练习9.如图,两个正方形ABDE和ACGF,点P为BC中点,连接PA交EF于点Q,试探究AP与EF的数量和位置关系,并证明你的结论.
课堂练习
例7.如图,△ABC中,AB=AC,点D在AB上,点E在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CE.
证明:如图,过点D作DG∥AE,交BC于点G;
则△DGF≌△ECF,
∴DG=CE;
∵AB=AC,
∴∠B=∠ACB;
∵DG∥AE,
∴∠DGB=∠ACB,
∴∠DBG=∠DGB,
∴DG=BD,
∴BD=CE.
例题讲解
练习9.如图,△ABC中,点D在AB上,E是AC延长线上一点,BD=CE,DE交BC于点F,DF=EF,DP∥AE交BC于点P,求证:AB=AC.
课堂练习
1、如图1已知:AD为△ABC的中线,易证AB+AC>2AD.
(1)如图2,在△ABC中,AC=5,AB=13,D为BC的中点,DA⊥AC.求△ABC的面积.
(2)问题2:如图3,在△ABC中,AD是三角形的中线.点F在中线AD上,且BF=AC,连接并延长BF交AC于点E.求证AE=EF.
课后练习
2.已知:如图,在四边形ABCD中,AB∥DC,E为BC边的中点,∠BAE=∠EAF,AF与DC的延长线相交于点F,试探究线段AB与AF,CF之间的数量关系,并说明理由.
课后练习
3.如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,求证:
(1)AE平分∠DAB;
(2)AB+CD=AD.
课后练习
4.在正方形ABCD的边AB上任取一点E,作EF⊥AB交BD于点F,取FD的中点G,连接EG、CG,如图(1),易证EG=CG且EG⊥CG.
(1)将△BEF绕点B逆时针旋转90°,如图(2),证明:EG=CG且EG⊥CG.
(2)如图(3)将△BEF绕点B逆时针旋转180°,证明:EG=CG且EG⊥CG.
课后练习
5.如图,△ABC中,AB=4,AC=7,M是BC的中点,AD平分∠BAC,过M作FM∥AD交AC于F,求FC的长.
课后练习
6.如图所示,∠BAC=∠DAE=90°,M是BE的中点,AB=AC,AD=AE,
求证:AM⊥CD.
课后练习
7.已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.
求证:∠DEN=∠F.
课后练习
2025年中考数学二轮复习专题
全等三角形之倍长中线法
当线段出现一个中点时,特别是三角形中,常常采用“倍长中线法”添加辅助线.倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.倍长中线法:△ABC中AD是BC边中线
方式1: 延长AD到E, 使DE=AD,连接BE
倍长中线法
例1.已知:如图,AD是△ABC的中线,求证:AB+AC>2AD.
证明:延长AD到M,使DM=AD,连接BM,CM,
∵AD是△ABC的中线,∴BD=DC,
∵AD=DM,∴四边形ABMC是平行四边形,
∴BM=AC,在△ABM中,AB+BM>AM,
即AB+AC>2AD.
例题讲解
例2.已知,如图△ABC中,AB=5,AC=3,则中线AD的取值范围是 .
解:延长AD到点E,使AD=ED,连接CE,∵AD是△ABC的中线,
∴BD=CD,在△ABD和△ECD中
∴△ABD≌△ECD(SAS),∴AB=EC,在△AEC中,AC+EC>AE,
且EC﹣AC<AE,即AB+AC>2AD,AB﹣AC<2AD,
∴2<2AD<8,∴1<AD<4,
故答案为:1<AD<4.
例题讲解
练习1.如图,在△ABC中,AC=5,中线AD=7,则AB边的取值范围是 .
课堂练习
例3.如图,△ABC中,∠A=90°,D为斜边BC的中点,E、F分别为AB、AC上的点,且DE⊥DF.若BE=3,CF=4,试求EF的长.
解:延长FD至点G,使得DG=DF,连接BG,EG,
∵在△CDF和△BDG中,
,
∴△CDF≌△BDG(SAS),
∴BG=CF=4,∠C=∠DBG,
∵∠C+∠ABC=90°,
∴∠DBG+∠ABC=90°,即∠ABG=90°,
∵DE⊥FG,DF=DG,
∴EF=EG=
=5.
例题讲解
练习2.如图,已知AD为△ABC的中线,DE平分∠ADB交AB于点E,DF平分∠ADC交AC于点F.求证:BE+CF>EF.
课堂练习
练习3.如图,在正方形ABCD中,E为AB边的中点,G,F分别为AD,BC边上的点,若AG=1,BF=2,∠GEF=90°,求GF的长.
课堂练习
练习4.如图,在梯形ABCD中,AD∥BC,点E在BC上,AE=BE,点F是CD的中点,且AF⊥AB,若AD=2.7,AF=4,AB=6.求CE的长.
课堂练习
例4.如图,在△ABC中,AB=AC,E是AB中点,延长AB到D,使BD=BA,延长CE至F,使得EF=CE.求证:CD=2CE.
证明:∵点E为AB的中点,∴BE=AE,
在△BEF和△AEC中,
∴△BEF≌△AEC(SAS),∴BF=AC,∠EBF=∠A,
∵AB=AC=BD,∴∠ACB=∠ABC,BF=BD,
∵∠CBD=∠A+∠ACB,∠CBF=∠ABC+∠EBF,∴∠CBD=∠CBF,
在△CBD和△CBF中,
∴△CBD≌△CBF(SAS),
∴CD=CF,∵CF=CE+EF,CE=EF,∴CF=2CE,∴CD=2CE.
例题讲解
练习5.已知:如图,在△ABC中,AB=AC,延长AB到D,使BD=AB,E为AB的中点.
求证:CD=2CE
课堂练习
练习6.已知CD=AB,∠BDA=∠BAD,AE是△ABD的中线,
求证:∠C=∠BAE.
课堂练习
练习7.如图,已知D是△ABC的边BC上的一点,CD=AB,∠BDA=∠BAD,AE是△ABD的中线.求证:AD是∠EAC的平分线.
课堂练习
例5.如图,在△ABC中,AD平分∠BAC,E为BC的中点,过点E作EF∥AD交AB于点G,交CA的延长线于点F.求证:BG=CF.
证明:作CM∥AB交FE的延长线于M.∵BG∥CM,
∴∠B=∠MCE,∵E是BC中点,
∴BE=EC,在△BEG和△CEM中,
∴△BEG≌△CEM,∴BG=CM,∵AD∥EF
∴∠1=∠FGA,
∠2=∠F,∵∠1=∠2,∴∠F=∠FGA,∵AB∥CM,
∴∠FGA=∠M,∴∠F=∠M,∴CF=CM,
∴BG=CF.
例题讲解
练习8.已知:如图,△ABC(AB≠AC)中,D、E在BC上,且DE=EC,过D作DF∥BA交AE于点F,DF=AC.求证:AE平分∠BAC.
课堂练习
例6.已知在△ABC中,AD是BC边上的中线,分别以AB边、AC边为直角边各向外作等腰直角三角形,如图,求证:EF=2AD.
证明:延长AD至点G,使得AD=DG,连接BG,CG,
∵AD=DG,BD=CD,∴四边形ABGC是平行四边形,
∴AC=AF=BG,AB=AE=CG,∠BAC+∠ABG=180°,
∵∠EAF+∠BAC=180°,∴∠EAF=∠ABG,
在△EAF和△BAG中,
∴△EAF≌△BAG(SAS)
∴EF=AG,
∵AG=2AD,
∴EF=2AD.
例题讲解
练习9.如图,两个正方形ABDE和ACGF,点P为BC中点,连接PA交EF于点Q,试探究AP与EF的数量和位置关系,并证明你的结论.
课堂练习
例7.如图,△ABC中,AB=AC,点D在AB上,点E在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CE.
证明:如图,过点D作DG∥AE,交BC于点G;
则△DGF≌△ECF,
∴DG=CE;
∵AB=AC,
∴∠B=∠ACB;
∵DG∥AE,
∴∠DGB=∠ACB,
∴∠DBG=∠DGB,
∴DG=BD,
∴BD=CE.
例题讲解
练习9.如图,△ABC中,点D在AB上,E是AC延长线上一点,BD=CE,DE交BC于点F,DF=EF,DP∥AE交BC于点P,求证:AB=AC.
课堂练习
1、如图1已知:AD为△ABC的中线,易证AB+AC>2AD.
(1)如图2,在△ABC中,AC=5,AB=13,D为BC的中点,DA⊥AC.求△ABC的面积.
(2)问题2:如图3,在△ABC中,AD是三角形的中线.点F在中线AD上,且BF=AC,连接并延长BF交AC于点E.求证AE=EF.
课后练习
2.已知:如图,在四边形ABCD中,AB∥DC,E为BC边的中点,∠BAE=∠EAF,AF与DC的延长线相交于点F,试探究线段AB与AF,CF之间的数量关系,并说明理由.
课后练习
3.如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,求证:
(1)AE平分∠DAB;
(2)AB+CD=AD.
课后练习
4.在正方形ABCD的边AB上任取一点E,作EF⊥AB交BD于点F,取FD的中点G,连接EG、CG,如图(1),易证EG=CG且EG⊥CG.
(1)将△BEF绕点B逆时针旋转90°,如图(2),证明:EG=CG且EG⊥CG.
(2)如图(3)将△BEF绕点B逆时针旋转180°,证明:EG=CG且EG⊥CG.
课后练习
5.如图,△ABC中,AB=4,AC=7,M是BC的中点,AD平分∠BAC,过M作FM∥AD交AC于F,求FC的长.
课后练习
6.如图所示,∠BAC=∠DAE=90°,M是BE的中点,AB=AC,AD=AE,
求证:AM⊥CD.
课后练习
7.已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.
求证:∠DEN=∠F.
课后练习
同课章节目录
