2025年中考数学二轮复习专题正方形中的半角模型 课件(共16张PPT)
文档属性
| 名称 | 2025年中考数学二轮复习专题正方形中的半角模型 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 616.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-03 05:47:14 | ||
图片预览




文档简介
(共16张PPT)
2025年中考数学二轮复习专题
正方形中的半角模型
例1.如图,已知正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45°.
求证:(1)EF=BE+DF;
(2)
证明:(1)延长CB到G,使GB=DF,连接AG(如图)
∵AB=AD,∠ABG=∠D=90°,GB=DF,
∴△ABG≌△ADF(SAS),
∴∠3=∠2,AG=AF,
∵∠BAD=90°,∠EAF=45°,
∴∠1+∠2=45°,
∴∠GAE=∠1+∠3=45°=∠EAF,
∵AE=AE,∠GAE=∠EAF,AG=AF,
∴△AGE≌△AFE(SAS),
∴GB+BE=EF,
∴DF+BE=EF;
例题讲解
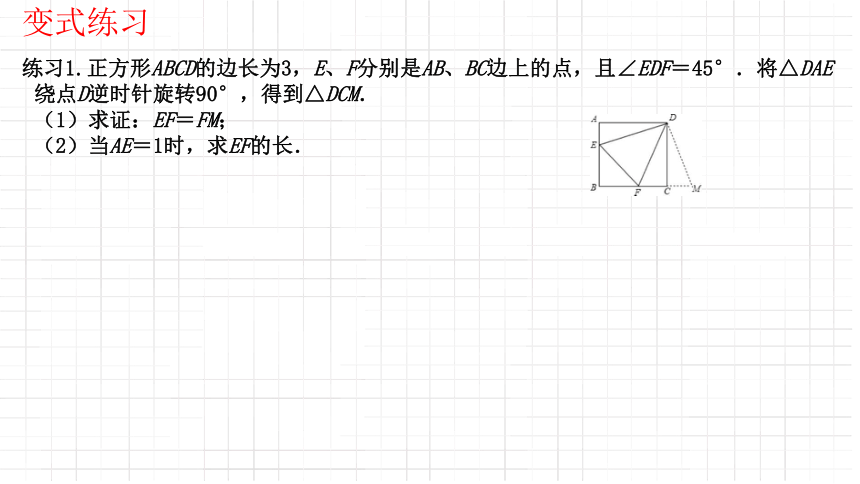
练习1.正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM;
(2)当AE=1时,求EF的长.
变式练习
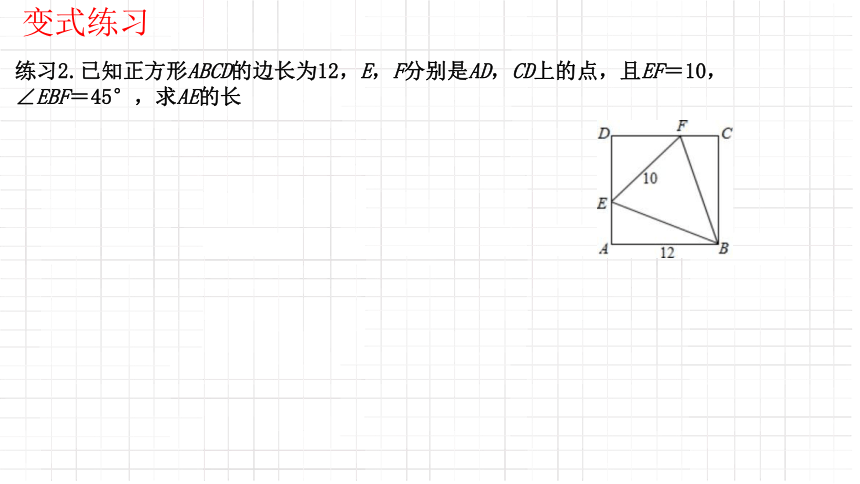
练习2.已知正方形ABCD的边长为12,E,F分别是AD,CD上的点,且EF=10,
∠EBF=45°,求AE的长
变式练习
例2.如图,已知边长为5正方形ABCD中,M、N分别为边BC、DC上的点,连接AM、AN,过N作NH⊥AM于点H,若∠ANH=45°,连接MN.
(1)证明:BM=MN﹣DN;
(2)求点A到MN的距离.
(1)证明:如图,延长CB至E,使得BE=DN,连接AE,
∵四边形ABCD是正方形,
∴AB=AD,
∠D=∠ABC=90°=∠ABE,
在△ADN和△ABE中
∴△ABE≌△ADN(SAS),
∴∠BAE=∠DAN,AE=AN,
∴∠EAN=∠BAE+∠BAN
=∠DAN+∠BAN=90°,
∵NH⊥AM于点H,若∠ANH=45°,
∴∠MAN=45°,
∴∠EAM=∠MAN=45°,
在△EAM和△NAM中,
∴△EAM≌△NAM(SAS),
∴MN=ME,
∴ME=BM+BE=BM+DN,
∴BM+DN=MN,
即BM=MN﹣DN;
(2)解:如图,过点A作AF⊥MN,
∵由(1)中△EAM≌△NAM得:
∠AMB=∠AMF,
又∵∠ABM=∠AFM=90°,AM=AM,
∴△ABM≌△AFM(AAS)
∴AB=AF=5,
即点A到MN的距离为5.
例题讲解
例3.已知正方形ABCD的边长为1,点M、N分别是边BC、CD的两点,若△CMN的周长为2,求:∠MAN的大小;
解:(1)延长CB到E,使BE=DN,连接AE,
∵四边形ABCD是正方形,
∴AD=AB,∠D=∠ABM=90°,
∴∠D=∠ABE=90°,
在△ADN和△ABE中,
∴△ADN≌△ABE(SAS),
∴AN=AE,∠DAN=∠BAE,
∵△CMN的周长为2,正方形ABCD的边长为1,
∵CM+CN+MN=2=CD+CB,
∴MN=2﹣CN﹣CM=DN+BM=ME,
在△NAM和△EAM中
∴△NAM≌△EAM(SSS),
∴∠NAM=∠EAM=∠BAM+∠EAB=
∠BAM+∠DAN=
=45°;
例题讲解
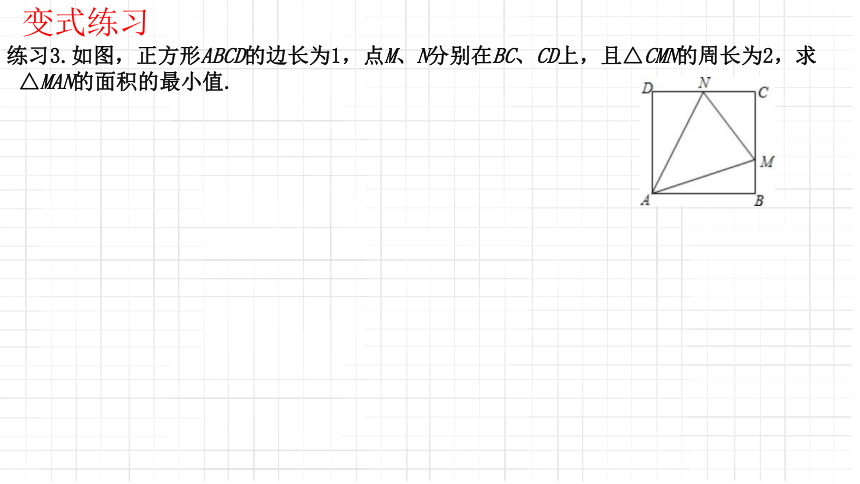
练习3.如图,正方形ABCD的边长为1,点M、N分别在BC、CD上,且△CMN的周长为2,求△MAN的面积的最小值.
变式练习
练习4.如图,已知正方形ABCD,M,N分别是BC,CD上的点,∠MAN=45°,连接BD分别交AM,AN于E,F,下面结论正确的是 .
①△CMN的周长等于正方形ABCD的边长的两倍;
②点A到MN的距离等于正方形ABCD的边长;
③EF2=BE2+DF2;
④△EMO与△FNO均为等腰直角三角形;
⑤S正方形ABCD:S△AMN=2AB:MN.
变式练习
例4.如图,已知Rt△ABC中,∠ACB=90°,AC=BC,点D、B在斜边AB上,
且∠DCE=45°,证明:DE2=BE2+AD2
证明:
如图,∵∠ACB=90°,AC=BC,
∴∠BAC=∠B=45°,
把△BCE绕点C逆时针旋转90°至△ACF,连接DF,
则△BCE≌△ACF,
∴AF=BE,∠CAF=∠B=45°,CF=CE,
∴∠DAF=∠CAF+∠BAC=90°,
在Rt△ADF中,由勾股定理得:DF2=AF2+AD2=BE2+AD2,
∴∠DCF=∠ECF﹣∠DCE=90°﹣45°=45°=∠DCE,
又∵CD=CD,
∴△CDF≌△CDE(SAS),
∴DE=DF,
∴DE2=BE2+AD2.
例题讲解
练习5.如图4.在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,若BD=1,EC=2,求DE的长.
.
变式练习
练习6.已知正方形ABCD,点E,F分别在边BC,CD上.∠EAF=∠CEF=45°,直线EF与AB,AD的延长线分别交于点M,N,求证:EF2=ME2+NF2
变式练习
例5.如图所示,过正方形ABCD的顶点A在正方形ABCD的内部作∠EAF=45°,E、F分别在BC、CD上,连接EF,作AH⊥EF于点H,求证:AH=AB.
证明:将△ADF绕点A顺时针旋转90°得到△ABG,
由旋转的性质得,DF=BG,AF=AG,∠DAF=∠BAG.
∵∠FAG=∠BAG+∠BAF=∠DAF+∠BAF=∠BAD=90°,
∠EAF=45°,
∴∠EAF=∠EAG=45°.
在△AEF和△AEG中,
∴△AEF≌△AEG(SAS),
∵AH、AB分别是△AEF和△AEG对应边上的高,
∴AH=AB.
例题讲解
例6.已知,正方形ABCD,M在CB延长线上,N在DC延长线上,∠MAN=45°.
求证:MN=DN﹣BM.
证明:如图,在DN上截取DE=MB,连接AE,
∵四边形ABCD是正方形,
∴AD=AB,∠D=∠ABM=90°,
在△ABM与△ADE中,
∴△ABM≌△ADE(SAS),
∴AM=AE,∠MAB=∠EAD,
∵∠MAN=45°=∠MAB+∠BAN,
∴∠DAE+∠BAN=45°,
∴∠EAN=90°﹣45°=45°=∠MAN,
在△AMN和△AEN中,
∴△AMN≌△AEN(SAS),
∴MN=EN,∵DN﹣DE=EN,
∴DN﹣BM=MN.
例题讲解
例7.点E,F分别是正方形ABCD中BC,CD延长线上的动点,且∠EAF=45°,
证明:BE=EF+DF;
证明:如图3,将△ADF绕点A逆时针旋转90°至△ABN,
∴AN=AF,∠NAF=90°,
∵∠EAF=45°,
∴∠NAE=45°,
∴∠NAE=∠FAE,
∵AE=AE,
∴△AFE≌△ANE(SAS),
∴EF=EN,
∴BE=BN+NE=DF+EF.
即BE=EF+DF.
例题讲解
练习7.已知:如图,在正方形ABCD中,M在CB延长线上,N在DC延长线上,∠MAN=45°,AH⊥MN,垂足为H,求证:(1)MN=DN﹣BM;
(2)AH=AB.
变式练习
练习8.在正方形ABCD中,如果点B,F分别是CB,DC延长线上的动点,
且∠EAF=45°,证明:EF=DF﹣BE;
变式练习
2025年中考数学二轮复习专题
正方形中的半角模型
例1.如图,已知正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45°.
求证:(1)EF=BE+DF;
(2)
证明:(1)延长CB到G,使GB=DF,连接AG(如图)
∵AB=AD,∠ABG=∠D=90°,GB=DF,
∴△ABG≌△ADF(SAS),
∴∠3=∠2,AG=AF,
∵∠BAD=90°,∠EAF=45°,
∴∠1+∠2=45°,
∴∠GAE=∠1+∠3=45°=∠EAF,
∵AE=AE,∠GAE=∠EAF,AG=AF,
∴△AGE≌△AFE(SAS),
∴GB+BE=EF,
∴DF+BE=EF;
例题讲解
练习1.正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM;
(2)当AE=1时,求EF的长.
变式练习
练习2.已知正方形ABCD的边长为12,E,F分别是AD,CD上的点,且EF=10,
∠EBF=45°,求AE的长
变式练习
例2.如图,已知边长为5正方形ABCD中,M、N分别为边BC、DC上的点,连接AM、AN,过N作NH⊥AM于点H,若∠ANH=45°,连接MN.
(1)证明:BM=MN﹣DN;
(2)求点A到MN的距离.
(1)证明:如图,延长CB至E,使得BE=DN,连接AE,
∵四边形ABCD是正方形,
∴AB=AD,
∠D=∠ABC=90°=∠ABE,
在△ADN和△ABE中
∴△ABE≌△ADN(SAS),
∴∠BAE=∠DAN,AE=AN,
∴∠EAN=∠BAE+∠BAN
=∠DAN+∠BAN=90°,
∵NH⊥AM于点H,若∠ANH=45°,
∴∠MAN=45°,
∴∠EAM=∠MAN=45°,
在△EAM和△NAM中,
∴△EAM≌△NAM(SAS),
∴MN=ME,
∴ME=BM+BE=BM+DN,
∴BM+DN=MN,
即BM=MN﹣DN;
(2)解:如图,过点A作AF⊥MN,
∵由(1)中△EAM≌△NAM得:
∠AMB=∠AMF,
又∵∠ABM=∠AFM=90°,AM=AM,
∴△ABM≌△AFM(AAS)
∴AB=AF=5,
即点A到MN的距离为5.
例题讲解
例3.已知正方形ABCD的边长为1,点M、N分别是边BC、CD的两点,若△CMN的周长为2,求:∠MAN的大小;
解:(1)延长CB到E,使BE=DN,连接AE,
∵四边形ABCD是正方形,
∴AD=AB,∠D=∠ABM=90°,
∴∠D=∠ABE=90°,
在△ADN和△ABE中,
∴△ADN≌△ABE(SAS),
∴AN=AE,∠DAN=∠BAE,
∵△CMN的周长为2,正方形ABCD的边长为1,
∵CM+CN+MN=2=CD+CB,
∴MN=2﹣CN﹣CM=DN+BM=ME,
在△NAM和△EAM中
∴△NAM≌△EAM(SSS),
∴∠NAM=∠EAM=∠BAM+∠EAB=
∠BAM+∠DAN=
=45°;
例题讲解
练习3.如图,正方形ABCD的边长为1,点M、N分别在BC、CD上,且△CMN的周长为2,求△MAN的面积的最小值.
变式练习
练习4.如图,已知正方形ABCD,M,N分别是BC,CD上的点,∠MAN=45°,连接BD分别交AM,AN于E,F,下面结论正确的是 .
①△CMN的周长等于正方形ABCD的边长的两倍;
②点A到MN的距离等于正方形ABCD的边长;
③EF2=BE2+DF2;
④△EMO与△FNO均为等腰直角三角形;
⑤S正方形ABCD:S△AMN=2AB:MN.
变式练习
例4.如图,已知Rt△ABC中,∠ACB=90°,AC=BC,点D、B在斜边AB上,
且∠DCE=45°,证明:DE2=BE2+AD2
证明:
如图,∵∠ACB=90°,AC=BC,
∴∠BAC=∠B=45°,
把△BCE绕点C逆时针旋转90°至△ACF,连接DF,
则△BCE≌△ACF,
∴AF=BE,∠CAF=∠B=45°,CF=CE,
∴∠DAF=∠CAF+∠BAC=90°,
在Rt△ADF中,由勾股定理得:DF2=AF2+AD2=BE2+AD2,
∴∠DCF=∠ECF﹣∠DCE=90°﹣45°=45°=∠DCE,
又∵CD=CD,
∴△CDF≌△CDE(SAS),
∴DE=DF,
∴DE2=BE2+AD2.
例题讲解
练习5.如图4.在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,若BD=1,EC=2,求DE的长.
.
变式练习
练习6.已知正方形ABCD,点E,F分别在边BC,CD上.∠EAF=∠CEF=45°,直线EF与AB,AD的延长线分别交于点M,N,求证:EF2=ME2+NF2
变式练习
例5.如图所示,过正方形ABCD的顶点A在正方形ABCD的内部作∠EAF=45°,E、F分别在BC、CD上,连接EF,作AH⊥EF于点H,求证:AH=AB.
证明:将△ADF绕点A顺时针旋转90°得到△ABG,
由旋转的性质得,DF=BG,AF=AG,∠DAF=∠BAG.
∵∠FAG=∠BAG+∠BAF=∠DAF+∠BAF=∠BAD=90°,
∠EAF=45°,
∴∠EAF=∠EAG=45°.
在△AEF和△AEG中,
∴△AEF≌△AEG(SAS),
∵AH、AB分别是△AEF和△AEG对应边上的高,
∴AH=AB.
例题讲解
例6.已知,正方形ABCD,M在CB延长线上,N在DC延长线上,∠MAN=45°.
求证:MN=DN﹣BM.
证明:如图,在DN上截取DE=MB,连接AE,
∵四边形ABCD是正方形,
∴AD=AB,∠D=∠ABM=90°,
在△ABM与△ADE中,
∴△ABM≌△ADE(SAS),
∴AM=AE,∠MAB=∠EAD,
∵∠MAN=45°=∠MAB+∠BAN,
∴∠DAE+∠BAN=45°,
∴∠EAN=90°﹣45°=45°=∠MAN,
在△AMN和△AEN中,
∴△AMN≌△AEN(SAS),
∴MN=EN,∵DN﹣DE=EN,
∴DN﹣BM=MN.
例题讲解
例7.点E,F分别是正方形ABCD中BC,CD延长线上的动点,且∠EAF=45°,
证明:BE=EF+DF;
证明:如图3,将△ADF绕点A逆时针旋转90°至△ABN,
∴AN=AF,∠NAF=90°,
∵∠EAF=45°,
∴∠NAE=45°,
∴∠NAE=∠FAE,
∵AE=AE,
∴△AFE≌△ANE(SAS),
∴EF=EN,
∴BE=BN+NE=DF+EF.
即BE=EF+DF.
例题讲解
练习7.已知:如图,在正方形ABCD中,M在CB延长线上,N在DC延长线上,∠MAN=45°,AH⊥MN,垂足为H,求证:(1)MN=DN﹣BM;
(2)AH=AB.
变式练习
练习8.在正方形ABCD中,如果点B,F分别是CB,DC延长线上的动点,
且∠EAF=45°,证明:EF=DF﹣BE;
变式练习
同课章节目录
