人教版2024—2025学年八年级上册人教版八年级上期第三次月考模拟试卷(含答案及评分标准)
文档属性
| 名称 | 人教版2024—2025学年八年级上册人教版八年级上期第三次月考模拟试卷(含答案及评分标准) |

|
|
| 格式 | docx | ||
| 文件大小 | 343.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-03 00:00:00 | ||
图片预览



文档简介
人教版2024—2025学年八年级上册人教版八年级上期第三次月考模拟试卷
考生注意:本次随堂练习共三道大题,25小题,满分120分,时量120分钟
一.选择题(本大题共10道题,每小题3分,共30分)
1.在以下节水、节能、回收、绿色食品四个标志中,是轴对称图形的是( )
A. B. C. D.
2.下列运算正确的是( )
A.2x2y+3xy=5x3y2 B.(﹣2ab2)3=﹣6a3b6
C.(3a+b)2=9a2+b2 D.(3a+b)(3a﹣b)=9a2﹣b2
3.在下列长度的三条线段中,不能组成三角形的是( )
A.2cm,3cm,4cm B.3cm,3cm,6cm
C.2cm,5cm,6cm D.5cm,6cm,7cm
化简分式的结果是( )
A. B. C. D.
5.若am=3,an=5,则am+n的值是( )
A. B. C.8 D.15
6.把多项式x2+ax+b分解因式,得(x+1)(x﹣3),则a,b的值分别是( )
A.a=﹣2,b=﹣3 B.a=2,b=3
C.a=﹣2,b=3 D.a=2,b=﹣3
7.如图,点P是∠BAC的平分线AD上一点,PE⊥AC于点E.已知PE=10,则点P到AB的距离是( )
A.15 B.12 C.5 D.10
8.如图,在△ABC和△DEF中,∠C=∠F=90°,添加下列条件,不能判定这两个三角形全等的是( )
A.∠A=∠D,∠B=∠E B.AC=DF,AB=DE
C.∠A=∠D,AB=DE D.AC=DF,CB=FE
9.如果把中的x与y都扩大为原来的5倍,那么这个代数式的值( )
A.不变 B.扩大为原来的5倍 C.缩小为原来的 D.扩大为原来的10倍
10.已知:a2﹣a﹣1=0,代数式的值( )
A.2019 B.2020 C.2021 D.2022
二、填空题(本大题共6道题,每小题3分,共18分)
11.因式分解:
12.若分式的值为0,则x= .
13.如图,在△ABC中,AB=AC,点D为BC边的中点,∠1=25°,则∠C的度数为 .
14.已知点和点关于x轴对称,则的值为 .
15.如图,在△ABC中,AB=AD=DC,∠BAD=20°,则∠C的度数为 .
16.如果代数式m2+2m=1,那么的值为 .
三、解答题(本大题共9道题,共72分)
17.(6分)计算:
18.(6分)先化简,再求值:,其中
19.(6分)如图,已知△ABC,∠C=90°,AC<BC,D为BC上一点,且到A,B两点的距离相等.
(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连接AD,若∠B=33°,则∠CAD= °.
(3)已知AB=13,的周长为17,则的周长为________.
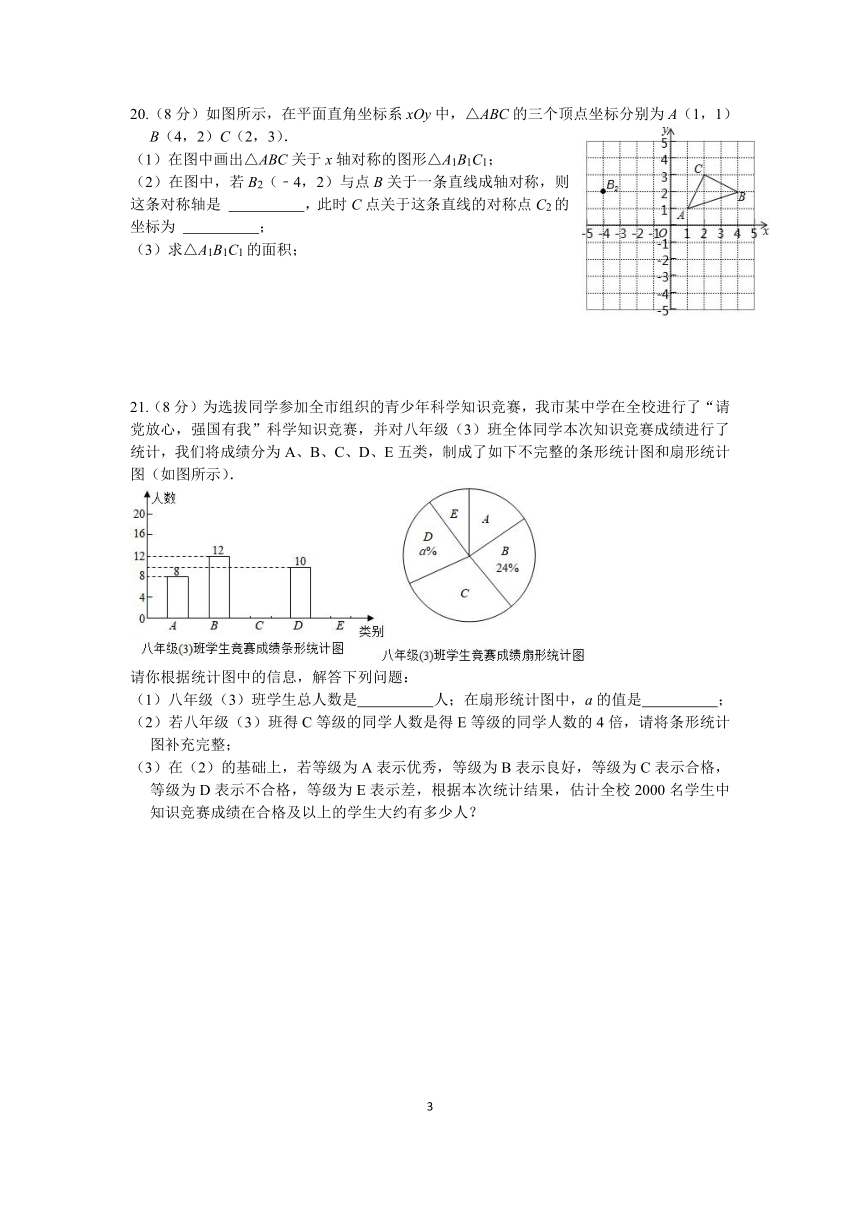
20.(8分)如图所示,在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(1,1)B(4,2)C(2,3).
(1)在图中画出△ABC关于x轴对称的图形△A1B1C1;
(2)在图中,若B2(﹣4,2)与点B关于一条直线成轴对称,则这条对称轴是 ,此时C点关于这条直线的对称点C2的坐标为 ;
(3)求△A1B1C1的面积;
21.(8分)为选拔同学参加全市组织的青少年科学知识竞赛,我市某中学在全校进行了“请党放心,强国有我”科学知识竞赛,并对八年级(3)班全体同学本次知识竞赛成绩进行了统计,我们将成绩分为A、B、C、D、E五类,制成了如下不完整的条形统计图和扇形统计图(如图所示).
请你根据统计图中的信息,解答下列问题:
(1)八年级(3)班学生总人数是 人;在扇形统计图中,a的值是 ;
(2)若八年级(3)班得C等级的同学人数是得E等级的同学人数的4倍,请将条形统计图补充完整;
(3)在(2)的基础上,若等级为A表示优秀,等级为B表示良好,等级为C表示合格,等级为D表示不合格,等级为E表示差,根据本次统计结果,估计全校2000名学生中知识竞赛成绩在合格及以上的学生大约有多少人?
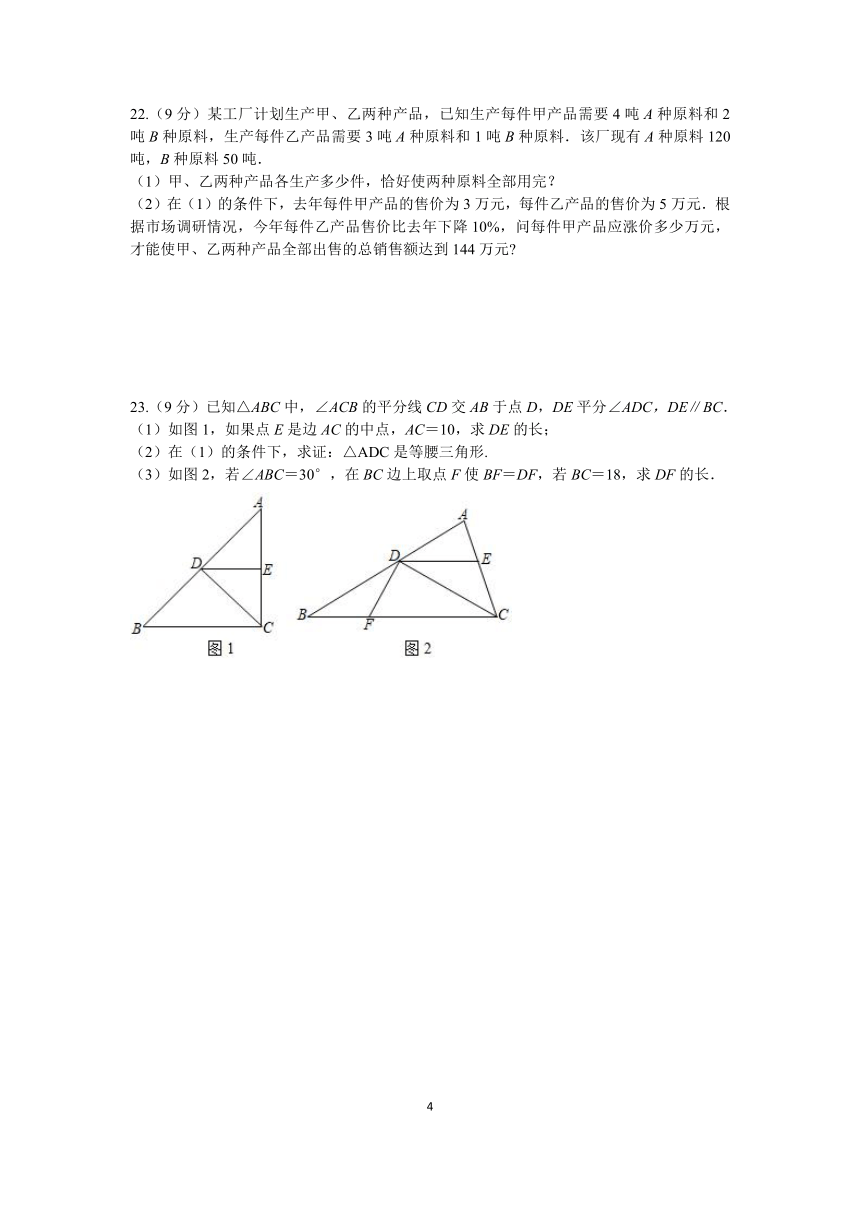
22.(9分)某工厂计划生产甲、乙两种产品,已知生产每件甲产品需要4吨A种原料和2吨B种原料,生产每件乙产品需要3吨A种原料和1吨B种原料.该厂现有A种原料120吨,B种原料50吨.
(1)甲、乙两种产品各生产多少件,恰好使两种原料全部用完?
(2)在(1)的条件下,去年每件甲产品的售价为3万元,每件乙产品的售价为5万元.根据市场调研情况,今年每件乙产品售价比去年下降10%,问每件甲产品应涨价多少万元,才能使甲、乙两种产品全部出售的总销售额达到144万元
23.(9分)已知△ABC中,∠ACB的平分线CD交AB于点D,DE平分∠ADC,DE∥BC.
(1)如图1,如果点E是边AC的中点,AC=10,求DE的长;
(2)在(1)的条件下,求证:△ADC是等腰三角形.
(3)如图2,若∠ABC=30°,在BC边上取点F使BF=DF,若BC=18,求DF的长.
24.(10分)若整式A只含有字母x,且A的次数不超过3次,令A=ax3+bx2+cx+d,其中a,b,c,d为整数,在平面直角坐标系中,我们定义:M(b+d,a+b+c+d)为整式A的阳光点,我们规定次数超过3次的整式没有中阳光点.例如,若整式A=2x2﹣5x+4,则a=0,b=2,c=﹣5,d=4,故A的阳光点为(6,1).
(1)若A=x3+x2﹣2x+4,则A的阳光点坐标为 .
(2)若整式,整式C是整式B与的乘积,求整式C的阳光点坐标。
(3)若整式D=x﹣3,整式E是只含有字母x的一次式,整式F是整式E的平方与整式D的乘积,若整式F的阳光点为(﹣3,﹣2),求整式E的表达式.
25.(10分)如图,在平面直角坐标系中,已知点A(a,0)、B(0,b)分别为x轴和y轴上一点,且a,b满足,过点B作BE⊥AC于点E,延长BE至点D,使得BD=AC,连接OC、OD.
(1) A点的坐标为 ;∠OAB的度数为 .
如图1,若点C在第四象限,试判断OC与OD的数量关系与位置关系,并说明理由.
如图2,连接CD,若点C的坐标为(4,3),CE平分∠OCD,AC与OD交于点F.
①求D点的坐标;
②试判断DE与CF的数量关系,并说明理由.
图1 图2
参考答案
一、选择题(每小题3分,共30分)
1—5:DDBBD 6—10:ADACC
二、填空题(每小题3分,共18分)
11. 12. 13. 14. 15. 16.
三、解答题
17.
19.解:(1)如图,点D即为所求;...............(2分)
(2)∵AD=BD,∠B=33°,
∴∠BAD=∠B=33°.
∵∠C=90°,
∴∠CAB=90°﹣∠B=90°﹣33°=57°,
∴∠CAD=∠CAB﹣∠BAD=57°﹣33°=24°.
故答案为:24..................................(4分)
(3)30......................(6分)
20.解:(1)略......................(3分)
(2)在图中,若B2(﹣4,2)与点B关于一条直线成轴对称,则这条对称轴是直线x=0,此时C点关于这条直线的对称点C2的坐标为(﹣2,3);
故答案为:直线x=0,(﹣2,3)..................................(5分)
(3)△A1B1C1的面积为=2×3﹣×1×2﹣×1×2﹣×1×3=,
故答案为:.................................(8分)
21.解:(1)八年级(3)班学生总人数是:12÷24%=50(人),
a%=×100%=20%,即a=20;
故答案为:50,20;...........(2分)
(2)设E等级的同学有x人,则C等级的同学人数有4x,根据题意得:
8+12+4x+10+x=50,解得:x=4,则4x=4×4=16,
则E等级的同学有4人,则C等级的同学人数有16人,
补全统计图如下:
......................(5分)
(3)2000×=1440(人),.................................(8分)
22.解:(1)设生产甲种产品x件,乙种产品y件,恰好使两种原料全部用完,
根据题意,得:,............................................(2分)
解得:,..........................................(4分)
答:生产甲种产品15件,乙种产品20件,恰好使两种原料全部用完.
(2)设每件甲种产品涨价m万元,才能使甲、乙两种产品全部出售的总销售额达到144万元,
根据题意,得:(3+m)×15+(1﹣10%)×5×20=144,..........................................(6分)
解得:m=0.6...........................................(8分)
答:每件甲产品应涨价0.6万元,才能使甲、乙两种产品全部出售的总销售额达到144万元.....................................................................................(9分)
23.解:(1)∵DC平分∠ACB,∴∠BCD=∠ACD,
∵DE∥BC,∴∠EDC=∠BCD,
∴∠EDC=∠ACD,∴ED=EC,
∵点E是边AC的中点,AC=10,∴EC=AC=5,∴DE=5;..............................(3分)
(2)
(3)∵DE∥BC,∴∠ADE=∠B,∠CDE=∠BCD,
∵DE平分∠ADC,∴∠ADE=∠CDE,∴∠B=∠BCD,∴DB=DC.
如图2,作DG⊥BC于点G,
∵DB=DC,DG⊥BC,
∴GB=BC=×18=9,
∵∠ABC=30°,BF=DF,
∴∠BDF=∠B=30°,.............................(7分)
∴∠DFG=∠B+∠BDF=60°,
∴∠FDG=30°,
∴BF=DF=2FG,
∴GF=3,
∴DF=2FG=6..............................(9分)
24.解:(1)(5,4)............................................(2分)
(2), .. 所以;......................(4分)
所以 ;
所以整式C的阳光点坐标为........................................(6分)
(3),设
所以
依题意,
化简得, ........................................(7分)
式式得:,即,
所以 因为所以..............(8分)
所以 ........................................(10分)
(1)(-6,0) ;45°........................................(2分)
OC=OD且OC⊥OD
证明:设AC、OB交于点G,由(1)知OA=OB
∵AC⊥BD,∠AOB=90°
∴∠AEB=∠AOB
而∠OGE=∠OBD+∠AEB=∠OAC+∠AOB
∴∠OBD=∠OAC
在△AOC和△BOD中,
........................................(3分)
∴△AOC≌△BOD(SAS)
∴OC=OD,∠AOC=∠BOD........................................(4分)
又∵∠AOC=∠AOB+∠BOC=∠COD+∠BOC=∠BOD
∴∠COD=∠AOB=90°
∴OC⊥OD.....................................(5分)
(3)①由(2)得OC=OD且OC⊥OD
过点D作DM⊥x轴于点M,过点C作CN⊥x轴于点N,
∵∠DOM+∠CON=90°=∠CON+∠OCN
∴∠DOM=∠OCN
在△DOM和△OCN中,
.....................................(6分)
∴△DOM≌△OCN(AAS)
∴DM=ON,OM=CN∵C点的坐标为(4,3)
∴DM=ON=4,OM=CN=3∴D(-3,4).....................................(7分)
②CF=2DE
延长CO交DB于点H,
∵CE平分∠OCD,AC⊥BD
∴∠OCF=∠DCF,∠CED=∠CEH=90°
∴∠CDH=∠CHD
∴CD=CH∴DE=EH=DH
又∵∠EFO=∠DEF+∠HDO=∠COF+∠FCO,∠DEF=∠COF=90°
∴∠HDO=∠FCO
在△DOH和△COF中,
.....................................(9分)
∴△DOH≌△COF(ASA)∴CF=DH=2DE.....................................(10分)
考生注意:本次随堂练习共三道大题,25小题,满分120分,时量120分钟
一.选择题(本大题共10道题,每小题3分,共30分)
1.在以下节水、节能、回收、绿色食品四个标志中,是轴对称图形的是( )
A. B. C. D.
2.下列运算正确的是( )
A.2x2y+3xy=5x3y2 B.(﹣2ab2)3=﹣6a3b6
C.(3a+b)2=9a2+b2 D.(3a+b)(3a﹣b)=9a2﹣b2
3.在下列长度的三条线段中,不能组成三角形的是( )
A.2cm,3cm,4cm B.3cm,3cm,6cm
C.2cm,5cm,6cm D.5cm,6cm,7cm
化简分式的结果是( )
A. B. C. D.
5.若am=3,an=5,则am+n的值是( )
A. B. C.8 D.15
6.把多项式x2+ax+b分解因式,得(x+1)(x﹣3),则a,b的值分别是( )
A.a=﹣2,b=﹣3 B.a=2,b=3
C.a=﹣2,b=3 D.a=2,b=﹣3
7.如图,点P是∠BAC的平分线AD上一点,PE⊥AC于点E.已知PE=10,则点P到AB的距离是( )
A.15 B.12 C.5 D.10
8.如图,在△ABC和△DEF中,∠C=∠F=90°,添加下列条件,不能判定这两个三角形全等的是( )
A.∠A=∠D,∠B=∠E B.AC=DF,AB=DE
C.∠A=∠D,AB=DE D.AC=DF,CB=FE
9.如果把中的x与y都扩大为原来的5倍,那么这个代数式的值( )
A.不变 B.扩大为原来的5倍 C.缩小为原来的 D.扩大为原来的10倍
10.已知:a2﹣a﹣1=0,代数式的值( )
A.2019 B.2020 C.2021 D.2022
二、填空题(本大题共6道题,每小题3分,共18分)
11.因式分解:
12.若分式的值为0,则x= .
13.如图,在△ABC中,AB=AC,点D为BC边的中点,∠1=25°,则∠C的度数为 .
14.已知点和点关于x轴对称,则的值为 .
15.如图,在△ABC中,AB=AD=DC,∠BAD=20°,则∠C的度数为 .
16.如果代数式m2+2m=1,那么的值为 .
三、解答题(本大题共9道题,共72分)
17.(6分)计算:
18.(6分)先化简,再求值:,其中
19.(6分)如图,已知△ABC,∠C=90°,AC<BC,D为BC上一点,且到A,B两点的距离相等.
(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连接AD,若∠B=33°,则∠CAD= °.
(3)已知AB=13,的周长为17,则的周长为________.
20.(8分)如图所示,在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(1,1)B(4,2)C(2,3).
(1)在图中画出△ABC关于x轴对称的图形△A1B1C1;
(2)在图中,若B2(﹣4,2)与点B关于一条直线成轴对称,则这条对称轴是 ,此时C点关于这条直线的对称点C2的坐标为 ;
(3)求△A1B1C1的面积;
21.(8分)为选拔同学参加全市组织的青少年科学知识竞赛,我市某中学在全校进行了“请党放心,强国有我”科学知识竞赛,并对八年级(3)班全体同学本次知识竞赛成绩进行了统计,我们将成绩分为A、B、C、D、E五类,制成了如下不完整的条形统计图和扇形统计图(如图所示).
请你根据统计图中的信息,解答下列问题:
(1)八年级(3)班学生总人数是 人;在扇形统计图中,a的值是 ;
(2)若八年级(3)班得C等级的同学人数是得E等级的同学人数的4倍,请将条形统计图补充完整;
(3)在(2)的基础上,若等级为A表示优秀,等级为B表示良好,等级为C表示合格,等级为D表示不合格,等级为E表示差,根据本次统计结果,估计全校2000名学生中知识竞赛成绩在合格及以上的学生大约有多少人?
22.(9分)某工厂计划生产甲、乙两种产品,已知生产每件甲产品需要4吨A种原料和2吨B种原料,生产每件乙产品需要3吨A种原料和1吨B种原料.该厂现有A种原料120吨,B种原料50吨.
(1)甲、乙两种产品各生产多少件,恰好使两种原料全部用完?
(2)在(1)的条件下,去年每件甲产品的售价为3万元,每件乙产品的售价为5万元.根据市场调研情况,今年每件乙产品售价比去年下降10%,问每件甲产品应涨价多少万元,才能使甲、乙两种产品全部出售的总销售额达到144万元
23.(9分)已知△ABC中,∠ACB的平分线CD交AB于点D,DE平分∠ADC,DE∥BC.
(1)如图1,如果点E是边AC的中点,AC=10,求DE的长;
(2)在(1)的条件下,求证:△ADC是等腰三角形.
(3)如图2,若∠ABC=30°,在BC边上取点F使BF=DF,若BC=18,求DF的长.
24.(10分)若整式A只含有字母x,且A的次数不超过3次,令A=ax3+bx2+cx+d,其中a,b,c,d为整数,在平面直角坐标系中,我们定义:M(b+d,a+b+c+d)为整式A的阳光点,我们规定次数超过3次的整式没有中阳光点.例如,若整式A=2x2﹣5x+4,则a=0,b=2,c=﹣5,d=4,故A的阳光点为(6,1).
(1)若A=x3+x2﹣2x+4,则A的阳光点坐标为 .
(2)若整式,整式C是整式B与的乘积,求整式C的阳光点坐标。
(3)若整式D=x﹣3,整式E是只含有字母x的一次式,整式F是整式E的平方与整式D的乘积,若整式F的阳光点为(﹣3,﹣2),求整式E的表达式.
25.(10分)如图,在平面直角坐标系中,已知点A(a,0)、B(0,b)分别为x轴和y轴上一点,且a,b满足,过点B作BE⊥AC于点E,延长BE至点D,使得BD=AC,连接OC、OD.
(1) A点的坐标为 ;∠OAB的度数为 .
如图1,若点C在第四象限,试判断OC与OD的数量关系与位置关系,并说明理由.
如图2,连接CD,若点C的坐标为(4,3),CE平分∠OCD,AC与OD交于点F.
①求D点的坐标;
②试判断DE与CF的数量关系,并说明理由.
图1 图2
参考答案
一、选择题(每小题3分,共30分)
1—5:DDBBD 6—10:ADACC
二、填空题(每小题3分,共18分)
11. 12. 13. 14. 15. 16.
三、解答题
17.
19.解:(1)如图,点D即为所求;...............(2分)
(2)∵AD=BD,∠B=33°,
∴∠BAD=∠B=33°.
∵∠C=90°,
∴∠CAB=90°﹣∠B=90°﹣33°=57°,
∴∠CAD=∠CAB﹣∠BAD=57°﹣33°=24°.
故答案为:24..................................(4分)
(3)30......................(6分)
20.解:(1)略......................(3分)
(2)在图中,若B2(﹣4,2)与点B关于一条直线成轴对称,则这条对称轴是直线x=0,此时C点关于这条直线的对称点C2的坐标为(﹣2,3);
故答案为:直线x=0,(﹣2,3)..................................(5分)
(3)△A1B1C1的面积为=2×3﹣×1×2﹣×1×2﹣×1×3=,
故答案为:.................................(8分)
21.解:(1)八年级(3)班学生总人数是:12÷24%=50(人),
a%=×100%=20%,即a=20;
故答案为:50,20;...........(2分)
(2)设E等级的同学有x人,则C等级的同学人数有4x,根据题意得:
8+12+4x+10+x=50,解得:x=4,则4x=4×4=16,
则E等级的同学有4人,则C等级的同学人数有16人,
补全统计图如下:
......................(5分)
(3)2000×=1440(人),.................................(8分)
22.解:(1)设生产甲种产品x件,乙种产品y件,恰好使两种原料全部用完,
根据题意,得:,............................................(2分)
解得:,..........................................(4分)
答:生产甲种产品15件,乙种产品20件,恰好使两种原料全部用完.
(2)设每件甲种产品涨价m万元,才能使甲、乙两种产品全部出售的总销售额达到144万元,
根据题意,得:(3+m)×15+(1﹣10%)×5×20=144,..........................................(6分)
解得:m=0.6...........................................(8分)
答:每件甲产品应涨价0.6万元,才能使甲、乙两种产品全部出售的总销售额达到144万元.....................................................................................(9分)
23.解:(1)∵DC平分∠ACB,∴∠BCD=∠ACD,
∵DE∥BC,∴∠EDC=∠BCD,
∴∠EDC=∠ACD,∴ED=EC,
∵点E是边AC的中点,AC=10,∴EC=AC=5,∴DE=5;..............................(3分)
(2)
(3)∵DE∥BC,∴∠ADE=∠B,∠CDE=∠BCD,
∵DE平分∠ADC,∴∠ADE=∠CDE,∴∠B=∠BCD,∴DB=DC.
如图2,作DG⊥BC于点G,
∵DB=DC,DG⊥BC,
∴GB=BC=×18=9,
∵∠ABC=30°,BF=DF,
∴∠BDF=∠B=30°,.............................(7分)
∴∠DFG=∠B+∠BDF=60°,
∴∠FDG=30°,
∴BF=DF=2FG,
∴GF=3,
∴DF=2FG=6..............................(9分)
24.解:(1)(5,4)............................................(2分)
(2), .. 所以;......................(4分)
所以 ;
所以整式C的阳光点坐标为........................................(6分)
(3),设
所以
依题意,
化简得, ........................................(7分)
式式得:,即,
所以 因为所以..............(8分)
所以 ........................................(10分)
(1)(-6,0) ;45°........................................(2分)
OC=OD且OC⊥OD
证明:设AC、OB交于点G,由(1)知OA=OB
∵AC⊥BD,∠AOB=90°
∴∠AEB=∠AOB
而∠OGE=∠OBD+∠AEB=∠OAC+∠AOB
∴∠OBD=∠OAC
在△AOC和△BOD中,
........................................(3分)
∴△AOC≌△BOD(SAS)
∴OC=OD,∠AOC=∠BOD........................................(4分)
又∵∠AOC=∠AOB+∠BOC=∠COD+∠BOC=∠BOD
∴∠COD=∠AOB=90°
∴OC⊥OD.....................................(5分)
(3)①由(2)得OC=OD且OC⊥OD
过点D作DM⊥x轴于点M,过点C作CN⊥x轴于点N,
∵∠DOM+∠CON=90°=∠CON+∠OCN
∴∠DOM=∠OCN
在△DOM和△OCN中,
.....................................(6分)
∴△DOM≌△OCN(AAS)
∴DM=ON,OM=CN∵C点的坐标为(4,3)
∴DM=ON=4,OM=CN=3∴D(-3,4).....................................(7分)
②CF=2DE
延长CO交DB于点H,
∵CE平分∠OCD,AC⊥BD
∴∠OCF=∠DCF,∠CED=∠CEH=90°
∴∠CDH=∠CHD
∴CD=CH∴DE=EH=DH
又∵∠EFO=∠DEF+∠HDO=∠COF+∠FCO,∠DEF=∠COF=90°
∴∠HDO=∠FCO
在△DOH和△COF中,
.....................................(9分)
∴△DOH≌△COF(ASA)∴CF=DH=2DE.....................................(10分)
同课章节目录
