2.3等差数列的前n项和
图片预览








文档简介
课件46张PPT。复习数列的有关概念复习回顾等差数列的概念等差数列的通项公式an=a1+(n-1)dan-an-1=d (n∈N*且 n≥2) 泰姬陵坐落于印度古都阿格,是十七世纪莫卧儿帝国皇帝沙杰罕为纪念其爱妃所建,她宏伟壮观,纯白大理石砌建而成的主体建筑叫人心醉神迷,成为世界七大奇迹之一。陵寝以宝石镶饰,图案之细致令人叫绝。
传说陵寝中有一个三角形图案,以相同大小的圆宝石镶饰而成,共有100层(见左图),奢靡之程度,可见一斑。你知道这个图案一共花了多少宝石吗?
探究发现2.3 等差数列的前n项和等差数列的前n项和 德国古代著名数学家高斯10岁的时候很快就解决了这个问题:1+2+3+…+100=?你知道高斯是怎样算出来的吗?高斯的算法计算: 1+ 2+ 3 +… + 99 + 100 高斯算法的高明之处在于他发现这100个数可以分为50组:
第一个数与最后一个数一组;
第二个数与倒数第二个数一组;
第三个数与倒数第三个数一组,……
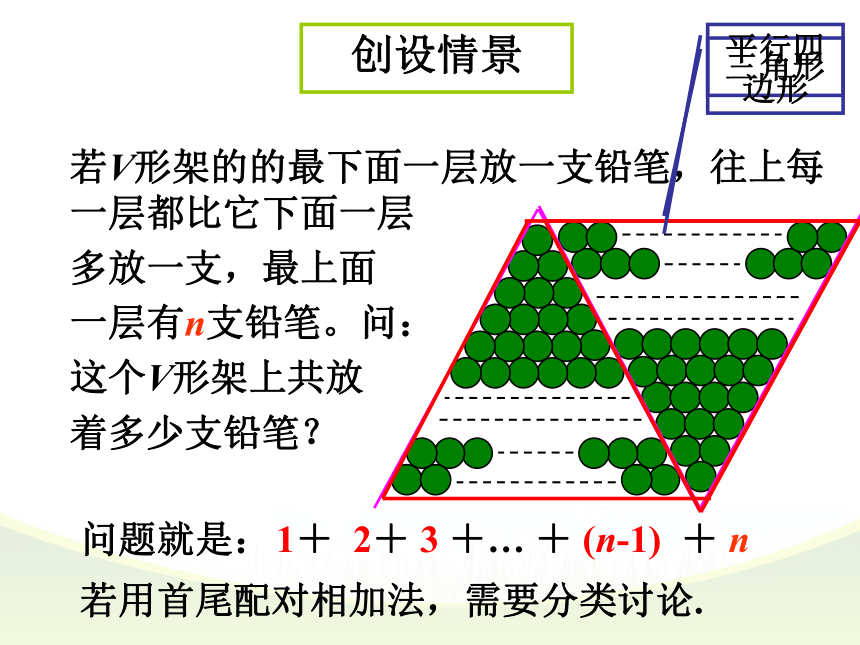
每组数的和均相等,都等于101,50个101就等于5050了。高斯算法将加法问题转化为乘法运算,迅速准确得到了结果.首尾配对相加法中间的一组数是什么呢?若V形架的的最下面一层放一支铅笔,往上每一层都比它下面一层
多放一支,最上面
一层有n支铅笔。问:
这个V形架上共放
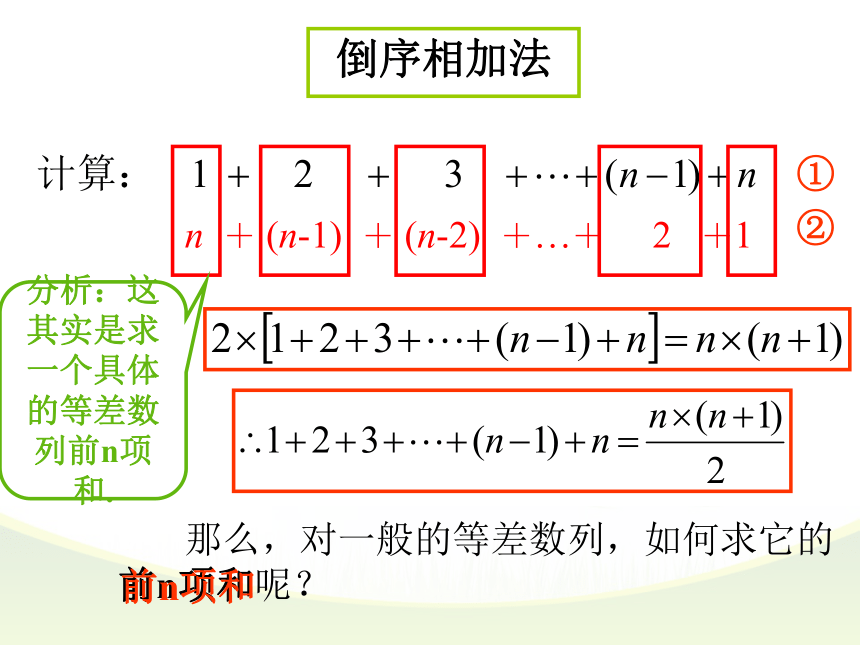
着多少支铅笔?创设情景问题就是:1+ 2+ 3 +… + (n-1) + n若用首尾配对相加法,需要分类讨论.三角形平行四边形n + (n-1) + (n-2) +…+ 2 +1倒序相加法 那么,对一般的等差数列,如何求它的
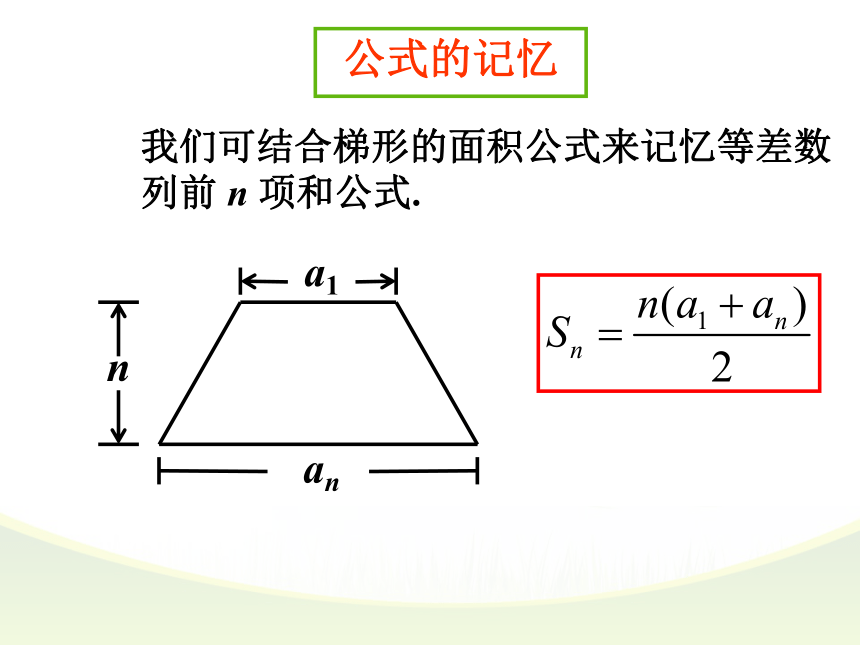
前n项和呢?前n项和分析:这其实是求一个具体的等差数列前n项和.①②问题分析已知等差数列{ an }的首项为a1,项数是n,第n项为an,求前n项和Sn .如何才能将等式的右边化简?①②已知等差数列{ an }的首项为a1,项数是n,第n项为an,求前n项和Sn .+++… + 各项组成新的等差数列①②倒序相加法求和公式等差数列的前n项和的公式:不含d可知三求一公式的记忆我们可结合梯形的面积公式来记忆等差数列前 n 项和公式.a1an(n-1)dana1公式的记忆我们可结合梯形的面积公式来记忆等差数列前 n 项和公式.a1将图形分割成一个平行四边形和一个三角形.求和公式 两个公式的共同点是需知 a1和 n,不同点是前者还需知 an,后者还需知 d,解题时需根据已知条件决定选用哪个公式。公式应用 根据下列各题中的条件,求相应的等差数列{an}的Sn :
(1)a1=5,an=95,n=10
(2)a1=100,d=-2,n=50练一练课本45页第1题例1、计算
(1) 5+6+7+…+79+80
(2) 1+3+5+…+(2n-1)
(3)1-2+3-4+5-6+…+(2n-1)-2n
-n例题讲解n23230提示:n=76法二:1.在等差数列{an},中,a1=25,b1=75,a100+b100=100,则数列的前100项的和为( )
A.0 B.100 C.1 000 D.10 000D【解析】a1+b1=100,a100+b100=100,∴S100=100×100=10 000.全优26页基础夯实2.(1)已知等差数列{an}的前5项之和为25,第8项等于15,求第21项;【解析】(1)a1+a2+…+a5=5a3=25,∴a3=5.∵a8=15,∴d=2,∴an=2n-1,∴a21=41.全优26页变式训练3.已知数列{an}中,a32+a82+2a3a8=9,且an<0,则S10为( )
A.-9 B.-11 C.-13 D.-15D【解析】(a3+a8)2=9,∵an<0,∴a3+a8=-3,全优26页基础夯实【例2】 在等差数列{an}中,(2)已知a11=-1,求S21;【解析】(2)∵a1+a21=2a11,a11=-1,∴a1+a21=-2.全优25页典例剖析4.设等差数列{an}的前n项和为Sn,若a5=5a3,9【解析】全优70页限时规范训练(二)2.若一个等差数列{an}的前3项和为34,最后3项的和为146且所有项的和为390,则这个数列有( )
A.13项 B.12项 C.11项 D.10项A【解析】a1+a2+a3+an-2+an-1+an=34+146=180,所以3(a1+an)=180,所以a1+an=60.解得n=13.全优70页限时规范训练(一)1.已知某等差数列共有10项,其奇数项之和为25,偶数项之和为50,则其公差为( )
A.6 B.5 C.4 D.3B【解析】依题意,得S偶-S奇=nd,可知其公差为5.全优70页限时规范训练(二)2.在各项均不为0的等差数列{an}中,若an+1-an2+an-1=0(n≥2),则S2n-1-4n=( )
A.-2 B.0 C.1 D.2A【解析】由an+1-an2+an-1=0(n≥2)可得2an-an2=0,解得an=2(零解舍去),故S2n-1-4n=2×(2n-1)-4n=-2. 全优70页限时规范训练(二)课本46页B组第2题1.已知等差数列{an}的前m项和为30,前2m项和为100,则数列的前3m项和为________.210解在等差数列中,Sm,S2m-Sm,S3m-S2m成等差数列.∴30,70,S3m-100成等差数列,∴2×70=30+S3m-100.∴S3m=210.全优28页变式训练例题讲解例2、已知一个等差数列的前10项的和是310,前20项的和是1220,由此可以确定求其前n项和的公式吗?解:由于S10=310,S20=1220,将它们代入公式可得所以例题讲解例2、已知一个等差数列的前10项的和是310,前20项的和是1220,由此可以确定求其前n项和的公式吗?另解: 两式相减得适用于任意数列注意:【例1】 已知数列{an}的前n项和Sn=3+2n,求an.【解析】∵Sn=3+2n,∴Sn-1=3+2n-1.∴an=Sn-Sn-1=2n-1(n≥2),而a1=S1=5,全优25页典例剖析观察例:如果等差数列的前4项和是4,前9项和是-6求前n项和的公式 。 解:令 等差数列的{an}前n项和的公式:【例1】 在等差数列{an}中,S10=100,S100=10,试求S110的值.【解析】解法一设等差数列{an}的首项为a1,公差为d.=-110.全优28页典例剖析【例1】 在等差数列{an}中,S10=100,S100=10,试求S110的值.【解析】解法二全优28页典例剖析设Sn=An2+Bn,【例1】 在等差数列{an}中,S10=100,S100=10,试求S110的值.【解析】解法三全优28页典例剖析∵S10=100,S100=10,∴S100-S10=a11+a12+…+a100∴a11+a100=-2.∴a1+a110=a11+a100=-2,说明:4.已知数列{an}的通项公式是an=2n-48,则Sn取得最小值时,n为________.23或24【解析】∵a24=0,∴a1+a2+…+a23<0,故S23=S24最小.全优26页基础夯实5.已知{an}是一个等差数列且a2=1,a5=-5.
(1)求{an}的通项an;【解析】(1)设{an}的公差为d,由已知条件,得解得a1=3,d=-2.所以an=a1+(n-1)d=-2n+5.(2)求{an}前n项和Sn的最大值.=-n2+4n=4-(n-2)2.所以当n=2时,Sn取得最大值4.全优70页限时规范训练(二)6.在等差数列{an}中,若a1=25,且S9=S17,求数列前多少项和最大.【解析】由S9=S17,得a1+a2+…+a9=a1+a2+…+a9+a10+…+a17,∴a10+a11+…+a17=0.∴4(a13+a14)=0,∴a13+a14=0.∴a13>0,a14<0,∴前13项和最大.全优29页基础夯实3.已知数列{an}中,Sn=-n2+10n,数列的每一项都有bn=|an|,求数列bn的前n项之和Tn的表达式.【解析】由Sn=-n2+10n,得an=Sn-Sn-1=11-2n,n∈N*且n≥2.验证a1=9成立.∴当n≤5时,an>0,此时Tn=Sn=-n2+10n;当n>5时,an<0,此时Tn=2S5-Sn=n2-10n+50.全优26页变式训练课本47页 4
传说陵寝中有一个三角形图案,以相同大小的圆宝石镶饰而成,共有100层(见左图),奢靡之程度,可见一斑。你知道这个图案一共花了多少宝石吗?
探究发现2.3 等差数列的前n项和等差数列的前n项和 德国古代著名数学家高斯10岁的时候很快就解决了这个问题:1+2+3+…+100=?你知道高斯是怎样算出来的吗?高斯的算法计算: 1+ 2+ 3 +… + 99 + 100 高斯算法的高明之处在于他发现这100个数可以分为50组:
第一个数与最后一个数一组;
第二个数与倒数第二个数一组;
第三个数与倒数第三个数一组,……
每组数的和均相等,都等于101,50个101就等于5050了。高斯算法将加法问题转化为乘法运算,迅速准确得到了结果.首尾配对相加法中间的一组数是什么呢?若V形架的的最下面一层放一支铅笔,往上每一层都比它下面一层
多放一支,最上面
一层有n支铅笔。问:
这个V形架上共放
着多少支铅笔?创设情景问题就是:1+ 2+ 3 +… + (n-1) + n若用首尾配对相加法,需要分类讨论.三角形平行四边形n + (n-1) + (n-2) +…+ 2 +1倒序相加法 那么,对一般的等差数列,如何求它的
前n项和呢?前n项和分析:这其实是求一个具体的等差数列前n项和.①②问题分析已知等差数列{ an }的首项为a1,项数是n,第n项为an,求前n项和Sn .如何才能将等式的右边化简?①②已知等差数列{ an }的首项为a1,项数是n,第n项为an,求前n项和Sn .+++… + 各项组成新的等差数列①②倒序相加法求和公式等差数列的前n项和的公式:不含d可知三求一公式的记忆我们可结合梯形的面积公式来记忆等差数列前 n 项和公式.a1an(n-1)dana1公式的记忆我们可结合梯形的面积公式来记忆等差数列前 n 项和公式.a1将图形分割成一个平行四边形和一个三角形.求和公式 两个公式的共同点是需知 a1和 n,不同点是前者还需知 an,后者还需知 d,解题时需根据已知条件决定选用哪个公式。公式应用 根据下列各题中的条件,求相应的等差数列{an}的Sn :
(1)a1=5,an=95,n=10
(2)a1=100,d=-2,n=50练一练课本45页第1题例1、计算
(1) 5+6+7+…+79+80
(2) 1+3+5+…+(2n-1)
(3)1-2+3-4+5-6+…+(2n-1)-2n
-n例题讲解n23230提示:n=76法二:1.在等差数列{an},中,a1=25,b1=75,a100+b100=100,则数列的前100项的和为( )
A.0 B.100 C.1 000 D.10 000D【解析】a1+b1=100,a100+b100=100,∴S100=100×100=10 000.全优26页基础夯实2.(1)已知等差数列{an}的前5项之和为25,第8项等于15,求第21项;【解析】(1)a1+a2+…+a5=5a3=25,∴a3=5.∵a8=15,∴d=2,∴an=2n-1,∴a21=41.全优26页变式训练3.已知数列{an}中,a32+a82+2a3a8=9,且an<0,则S10为( )
A.-9 B.-11 C.-13 D.-15D【解析】(a3+a8)2=9,∵an<0,∴a3+a8=-3,全优26页基础夯实【例2】 在等差数列{an}中,(2)已知a11=-1,求S21;【解析】(2)∵a1+a21=2a11,a11=-1,∴a1+a21=-2.全优25页典例剖析4.设等差数列{an}的前n项和为Sn,若a5=5a3,9【解析】全优70页限时规范训练(二)2.若一个等差数列{an}的前3项和为34,最后3项的和为146且所有项的和为390,则这个数列有( )
A.13项 B.12项 C.11项 D.10项A【解析】a1+a2+a3+an-2+an-1+an=34+146=180,所以3(a1+an)=180,所以a1+an=60.解得n=13.全优70页限时规范训练(一)1.已知某等差数列共有10项,其奇数项之和为25,偶数项之和为50,则其公差为( )
A.6 B.5 C.4 D.3B【解析】依题意,得S偶-S奇=nd,可知其公差为5.全优70页限时规范训练(二)2.在各项均不为0的等差数列{an}中,若an+1-an2+an-1=0(n≥2),则S2n-1-4n=( )
A.-2 B.0 C.1 D.2A【解析】由an+1-an2+an-1=0(n≥2)可得2an-an2=0,解得an=2(零解舍去),故S2n-1-4n=2×(2n-1)-4n=-2. 全优70页限时规范训练(二)课本46页B组第2题1.已知等差数列{an}的前m项和为30,前2m项和为100,则数列的前3m项和为________.210解在等差数列中,Sm,S2m-Sm,S3m-S2m成等差数列.∴30,70,S3m-100成等差数列,∴2×70=30+S3m-100.∴S3m=210.全优28页变式训练例题讲解例2、已知一个等差数列的前10项的和是310,前20项的和是1220,由此可以确定求其前n项和的公式吗?解:由于S10=310,S20=1220,将它们代入公式可得所以例题讲解例2、已知一个等差数列的前10项的和是310,前20项的和是1220,由此可以确定求其前n项和的公式吗?另解: 两式相减得适用于任意数列注意:【例1】 已知数列{an}的前n项和Sn=3+2n,求an.【解析】∵Sn=3+2n,∴Sn-1=3+2n-1.∴an=Sn-Sn-1=2n-1(n≥2),而a1=S1=5,全优25页典例剖析观察例:如果等差数列的前4项和是4,前9项和是-6求前n项和的公式 。 解:令 等差数列的{an}前n项和的公式:【例1】 在等差数列{an}中,S10=100,S100=10,试求S110的值.【解析】解法一设等差数列{an}的首项为a1,公差为d.=-110.全优28页典例剖析【例1】 在等差数列{an}中,S10=100,S100=10,试求S110的值.【解析】解法二全优28页典例剖析设Sn=An2+Bn,【例1】 在等差数列{an}中,S10=100,S100=10,试求S110的值.【解析】解法三全优28页典例剖析∵S10=100,S100=10,∴S100-S10=a11+a12+…+a100∴a11+a100=-2.∴a1+a110=a11+a100=-2,说明:4.已知数列{an}的通项公式是an=2n-48,则Sn取得最小值时,n为________.23或24【解析】∵a24=0,∴a1+a2+…+a23<0,故S23=S24最小.全优26页基础夯实5.已知{an}是一个等差数列且a2=1,a5=-5.
(1)求{an}的通项an;【解析】(1)设{an}的公差为d,由已知条件,得解得a1=3,d=-2.所以an=a1+(n-1)d=-2n+5.(2)求{an}前n项和Sn的最大值.=-n2+4n=4-(n-2)2.所以当n=2时,Sn取得最大值4.全优70页限时规范训练(二)6.在等差数列{an}中,若a1=25,且S9=S17,求数列前多少项和最大.【解析】由S9=S17,得a1+a2+…+a9=a1+a2+…+a9+a10+…+a17,∴a10+a11+…+a17=0.∴4(a13+a14)=0,∴a13+a14=0.∴a13>0,a14<0,∴前13项和最大.全优29页基础夯实3.已知数列{an}中,Sn=-n2+10n,数列的每一项都有bn=|an|,求数列bn的前n项之和Tn的表达式.【解析】由Sn=-n2+10n,得an=Sn-Sn-1=11-2n,n∈N*且n≥2.验证a1=9成立.∴当n≤5时,an>0,此时Tn=Sn=-n2+10n;当n>5时,an<0,此时Tn=2S5-Sn=n2-10n+50.全优26页变式训练课本47页 4
