华师大版七下(2024版)7.1.2不等式的解集
文档属性
| 名称 | 华师大版七下(2024版)7.1.2不等式的解集 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-07 00:00:00 | ||
图片预览






文档简介
(共29张PPT)
第七章 一元一次不等式
7.1.2不等式的解集
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
让学生能根据具体情境理解不等式的解与解集的意义.
01
2.让学生能在数轴上表示不等式的解集.
02
经历求不等式的解集的过程,通过尝试把不等式的解集在数轴上表示出来,引导学生体验用数轴表示不等式的解集具有直观的优越性,增强学生数形结合的意识.
03
02
新知导入
复习回顾:什么是方程的解?
使方程两边相等的未知数的值就是方程的解
与方程类似, 能使不等式成立的未知数的值叫不等式的解.
代入法是检验某个值是否是不等式的解的简单、实用的方法.
03
新知讲解
不等式 ,除了上面提到的解之外,你还可以说出它的那些解
探究
不等式的解集
解有( )个
下列各数中,那些是不等式的解?
-3, -4, -1, 0, 1.5, 2.5, -5, -6, -7
无数
03
新知讲解
实际上,小于的每一个数都是不等式的解,而不小于的每一个数都不是不等式的解。不等式的解有无数个,它们组成一个集合,称为不等式的解集。
你知道上面例题中其他不等式的解集是由哪些数组成的吗
一个不等式的所有解,组成这个不等式的解的集合,简称为这个不等式的解集(solution set).
概括
不等式的解集必须满足两个条件:
1.解集中的任何一个数值都使不等式成立;
2.解集外的任何一个数值都不能使不等式成立.
注意
03
新知讲解
研究不等式的一个重要任务,就是求出不等式的解集,求不等式的解集的过程,叫做解不等式.
03
新知探究
不等式的解和不等式的解集有什么区别和联系
03
新知探究
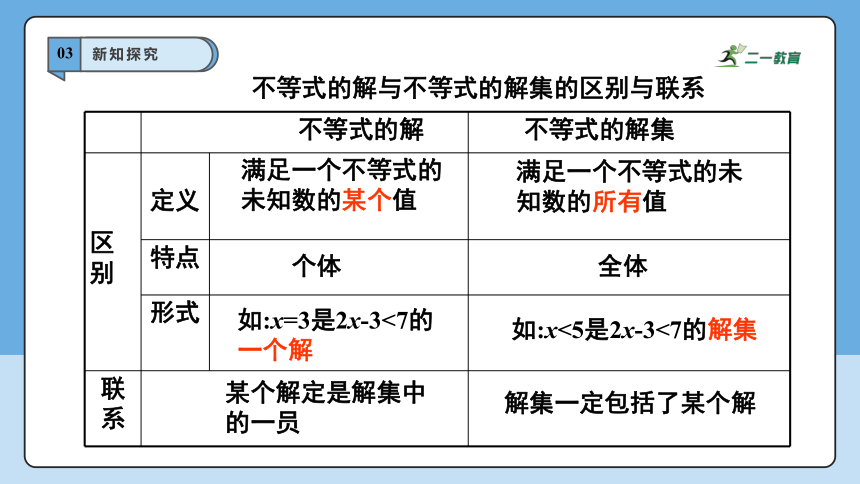
不等式的解与不等式的解集的区别与联系
不等式的解 不等式的解集
区别 定义
特点
形式
联系
满足一个不等式的未知数的某个值
满足一个不等式的未知数的所有值
个体
全体
如:x=3是2x-3<7的一个解
如:x<5是2x-3<7的解集
某个解定是解集中的一员
解集一定包括了某个解
03
新知探究
例如, 由上面的讨论可知, 不等式 的解集为 , 可以在数轴上直观地表示出来, 如图 所示.
03
新知探究
再如, 不等式 的解集, 它也可以在数轴上直观地表示出来, 如图 所示.
03
新知探究
比较图 与图 , 它们有什么区别
解集不包括,在处画___________。
解集包括,在处画___________。
空心圆圈
实心圆点
一般地,解集,表示“小于或等于”,或者说“不大于”.
类似地,解集,表示“大于或等于”,或者说“不小于”.
注意
03
新知探究
这里,出现了符号“≤”. 一般地,解集x ≤ a,表示“x小于或等于a”,或者说“x不大于a”. 类似地,解集x ≥ a,表示“x大于或等于a”,或者说“x不小于a”.在数轴上,解集x ≤ a,是指表示数 a 的点左边的部分,包括表示数 a 的点在内,这一点画成实心圆点.而解集x < a,则是指表示数 a 的点左边的部分,但不包括表示数 a 的点,这一点画成空心圆圈. 对于解集x ≥ a和x > a在数轴上的表示,与此相仿.
03
新知讲解
不等式的解集在数轴上的表示方法有以下几种:
不等式的解集 数轴表示 注意
x>a 端点用空心圆圈,方向向右
x<a 端点用空心圆圈,方向向左
x ≥ a 端点用实心圆点,方向向右
x ≤ a 端点用实心圆点,方向向左
03
新知讲解
利用数轴来表示下列不等式的解集.
; .
分析
结合不等式解集在数轴上的表示方法,可以用口诀:“大于向右,小于向左,有等实心,无等空心”确定“界点”与“方向”.
0
-1
0
1
表示-1的点
表示的点
方向向右
方向向左
空心圆表示不含此点
03
例题讲解
直接写出的解集,并在数轴上表示出来.
例
解:不等式的解集为,将解集表示在数轴上如图所示.
思考:将解集表示在数轴上需要注意哪些地方?
03
新知讲解
(1)在定方向时,要注意不要搞错方向,大于向右.小于向左.
(2)有等于号(≤,≥)画实心圆点,无等于号(<,>)画空心圆圈.
(3)在数轴上表示不等式的解集,一般分三步:画数轴,定界点,定方向.
用数轴表示不等式的解集的要点:
04
课堂练习
2.不等式的解集在数轴上表示正确的是( )
A B C D
【知识技能类作业】必做题:
1.下列的值中,能使不等式成立的是( )
A.-3 B.2 C.3 D.5
A
C
3.满足的最大整数是( )
A.1 B.2 C.3 D.4
C
04
课堂练习
【知识技能类作业】选做题:
4.如图,数轴上表示的取值范围是 .
5.请你写出满足不等式的个解: .
-1、-0.5、0、1.5、4(答案不唯一,小于8即可)
04
课堂练习
【综合拓展类作业】
6.不等式的非负整数解是 ;不等式的最大整数解是 .
05
课堂小结
不等式
一个不等式的所有解,组成这个不等式的解的集合.
不等式的解集
1、用简单的不等式表示;
不等式解集的表示
2、用数轴表示:一是确定“界点”,二是确定“方向”
06
作业布置
【知识技能类作业】必做题:
1.方程的解有 个,不等式的解有 个.
2.判断题.
(1)是不等式的一个解;( )
(2)是不等式的解集; ( )
(3)不等式的解集是; ( )
(4)不等式的解集是. ( )
1
正确
无数
错误
错误
正确
3.将下列不等式分别表示在数轴上:
(1) ; (2) ; (3); (4).
06
作业布置
【知识技能类作业】必做题:
解:(1)如图所示.
(2)如图所示.
(3)如图所示.
(4)如图所示.
06
作业布置
【知识技能类作业】选做题:
4.已知,则的取值范围在数轴上表示正确的是( )
A B C D
A
5.试写出一个不等式,使它的解集满足下列条件:
(1)不等式的正整数解只有;
(2)不等式的整数解只有.
(1)答案不唯一,如x<4,x<3.99.
(2)答案不唯一,如-3<x≤1,-2.1<x<1.1.
06
作业布置
【综合拓展类作业】
6.国际上广泛使用“身体体重指数(BMI)”作为判断人体健康状况的一个指标:这个指数B等于人体的体重G(单位:kg)除以人体的身高h(单位:m)的平方所得的商.
身体体重指数范围 身体属型
B<18 不健康瘦弱
18≤B<20 偏瘦
20≤B<25 正常
25≤B<30 超重
B≥30 不健康肥胖
06
作业布置
【综合拓展类作业】
(1)写出身体体重指数B与G、h之间的关系式.
(2)上表是国内某健康组织提供的参考标准.若林老师的体重,身高,他的身体属型属于哪一种?
解:(1)由题意可列B=
(2),
故林老师的身体属型属于超重型.
06
作业布置
【综合拓展类作业】
(3),,则,
计算得:
故赵老师的体重在时,身体属型属于正常.
(3)赵老师的身高为,那么他的体重在什么范围内时,身体属型属于正常?
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第七章 一元一次不等式
7.1.2不等式的解集
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
让学生能根据具体情境理解不等式的解与解集的意义.
01
2.让学生能在数轴上表示不等式的解集.
02
经历求不等式的解集的过程,通过尝试把不等式的解集在数轴上表示出来,引导学生体验用数轴表示不等式的解集具有直观的优越性,增强学生数形结合的意识.
03
02
新知导入
复习回顾:什么是方程的解?
使方程两边相等的未知数的值就是方程的解
与方程类似, 能使不等式成立的未知数的值叫不等式的解.
代入法是检验某个值是否是不等式的解的简单、实用的方法.
03
新知讲解
不等式 ,除了上面提到的解之外,你还可以说出它的那些解
探究
不等式的解集
解有( )个
下列各数中,那些是不等式的解?
-3, -4, -1, 0, 1.5, 2.5, -5, -6, -7
无数
03
新知讲解
实际上,小于的每一个数都是不等式的解,而不小于的每一个数都不是不等式的解。不等式的解有无数个,它们组成一个集合,称为不等式的解集。
你知道上面例题中其他不等式的解集是由哪些数组成的吗
一个不等式的所有解,组成这个不等式的解的集合,简称为这个不等式的解集(solution set).
概括
不等式的解集必须满足两个条件:
1.解集中的任何一个数值都使不等式成立;
2.解集外的任何一个数值都不能使不等式成立.
注意
03
新知讲解
研究不等式的一个重要任务,就是求出不等式的解集,求不等式的解集的过程,叫做解不等式.
03
新知探究
不等式的解和不等式的解集有什么区别和联系
03
新知探究
不等式的解与不等式的解集的区别与联系
不等式的解 不等式的解集
区别 定义
特点
形式
联系
满足一个不等式的未知数的某个值
满足一个不等式的未知数的所有值
个体
全体
如:x=3是2x-3<7的一个解
如:x<5是2x-3<7的解集
某个解定是解集中的一员
解集一定包括了某个解
03
新知探究
例如, 由上面的讨论可知, 不等式 的解集为 , 可以在数轴上直观地表示出来, 如图 所示.
03
新知探究
再如, 不等式 的解集, 它也可以在数轴上直观地表示出来, 如图 所示.
03
新知探究
比较图 与图 , 它们有什么区别
解集不包括,在处画___________。
解集包括,在处画___________。
空心圆圈
实心圆点
一般地,解集,表示“小于或等于”,或者说“不大于”.
类似地,解集,表示“大于或等于”,或者说“不小于”.
注意
03
新知探究
这里,出现了符号“≤”. 一般地,解集x ≤ a,表示“x小于或等于a”,或者说“x不大于a”. 类似地,解集x ≥ a,表示“x大于或等于a”,或者说“x不小于a”.在数轴上,解集x ≤ a,是指表示数 a 的点左边的部分,包括表示数 a 的点在内,这一点画成实心圆点.而解集x < a,则是指表示数 a 的点左边的部分,但不包括表示数 a 的点,这一点画成空心圆圈. 对于解集x ≥ a和x > a在数轴上的表示,与此相仿.
03
新知讲解
不等式的解集在数轴上的表示方法有以下几种:
不等式的解集 数轴表示 注意
x>a 端点用空心圆圈,方向向右
x<a 端点用空心圆圈,方向向左
x ≥ a 端点用实心圆点,方向向右
x ≤ a 端点用实心圆点,方向向左
03
新知讲解
利用数轴来表示下列不等式的解集.
; .
分析
结合不等式解集在数轴上的表示方法,可以用口诀:“大于向右,小于向左,有等实心,无等空心”确定“界点”与“方向”.
0
-1
0
1
表示-1的点
表示的点
方向向右
方向向左
空心圆表示不含此点
03
例题讲解
直接写出的解集,并在数轴上表示出来.
例
解:不等式的解集为,将解集表示在数轴上如图所示.
思考:将解集表示在数轴上需要注意哪些地方?
03
新知讲解
(1)在定方向时,要注意不要搞错方向,大于向右.小于向左.
(2)有等于号(≤,≥)画实心圆点,无等于号(<,>)画空心圆圈.
(3)在数轴上表示不等式的解集,一般分三步:画数轴,定界点,定方向.
用数轴表示不等式的解集的要点:
04
课堂练习
2.不等式的解集在数轴上表示正确的是( )
A B C D
【知识技能类作业】必做题:
1.下列的值中,能使不等式成立的是( )
A.-3 B.2 C.3 D.5
A
C
3.满足的最大整数是( )
A.1 B.2 C.3 D.4
C
04
课堂练习
【知识技能类作业】选做题:
4.如图,数轴上表示的取值范围是 .
5.请你写出满足不等式的个解: .
-1、-0.5、0、1.5、4(答案不唯一,小于8即可)
04
课堂练习
【综合拓展类作业】
6.不等式的非负整数解是 ;不等式的最大整数解是 .
05
课堂小结
不等式
一个不等式的所有解,组成这个不等式的解的集合.
不等式的解集
1、用简单的不等式表示;
不等式解集的表示
2、用数轴表示:一是确定“界点”,二是确定“方向”
06
作业布置
【知识技能类作业】必做题:
1.方程的解有 个,不等式的解有 个.
2.判断题.
(1)是不等式的一个解;( )
(2)是不等式的解集; ( )
(3)不等式的解集是; ( )
(4)不等式的解集是. ( )
1
正确
无数
错误
错误
正确
3.将下列不等式分别表示在数轴上:
(1) ; (2) ; (3); (4).
06
作业布置
【知识技能类作业】必做题:
解:(1)如图所示.
(2)如图所示.
(3)如图所示.
(4)如图所示.
06
作业布置
【知识技能类作业】选做题:
4.已知,则的取值范围在数轴上表示正确的是( )
A B C D
A
5.试写出一个不等式,使它的解集满足下列条件:
(1)不等式的正整数解只有;
(2)不等式的整数解只有.
(1)答案不唯一,如x<4,x<3.99.
(2)答案不唯一,如-3<x≤1,-2.1<x<1.1.
06
作业布置
【综合拓展类作业】
6.国际上广泛使用“身体体重指数(BMI)”作为判断人体健康状况的一个指标:这个指数B等于人体的体重G(单位:kg)除以人体的身高h(单位:m)的平方所得的商.
身体体重指数范围 身体属型
B<18 不健康瘦弱
18≤B<20 偏瘦
20≤B<25 正常
25≤B<30 超重
B≥30 不健康肥胖
06
作业布置
【综合拓展类作业】
(1)写出身体体重指数B与G、h之间的关系式.
(2)上表是国内某健康组织提供的参考标准.若林老师的体重,身高,他的身体属型属于哪一种?
解:(1)由题意可列B=
(2),
故林老师的身体属型属于超重型.
06
作业布置
【综合拓展类作业】
(3),,则,
计算得:
故赵老师的体重在时,身体属型属于正常.
(3)赵老师的身高为,那么他的体重在什么范围内时,身体属型属于正常?
Thanks!
https://www.21cnjy.com/recruitment/home/fine
