冀教版(2024)七年级数学下册 第七章 相交线与平行线 单元测试题(含解析)
文档属性
| 名称 | 冀教版(2024)七年级数学下册 第七章 相交线与平行线 单元测试题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 517.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-05 08:28:14 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
冀教版七年级数学下册 第七章 相交线与平行线 单元测试题(2024)
一、选择题(共10题;共30分)
1.(3分)下列命题中,假命题的是( ).
A.顺次连接对角线相等的四边形的四边中点所形成的图形是菱形;
B.各边对应成比例的两个多边形相似;
C.反比例函数的图象既是轴对轴图形,也是中心对称图形;
D.已知二次函数,当时,y随x的增大而减小.
2.(3分)如图,三角形ABC中,,于点D,若,则点C到直线AB的距离是( )
A. B.3 C.4 D.5
3.(3分)下面四个图是小明用尺规过点C作AB边的平行线所留下的作图痕迹,其中正确的是( )
A. B.
C. D.
4.(3分)如图,直线a,b被直线c所截,下列条件中,不能判定a∥b的是( )
A.∠2=∠5 B.∠1=∠3
C.∠5=∠4 D.∠1+∠5=180°
5.(3分)如图,鸿鸿同学在使用量角器时操作不规范,请你根据她的测量图估计的度数可能是( )
A. B. C. D.
6.(3分)如图,将沿射线方向移动,使点移动到点,得到,连接,若的面积为2,则的面积为( )
A.2 B.4 C.6 D.16
7.(3分)如图,,则下列结论正确的是( )
A. B. C. D.
8.(3分) 过点 作直线 的平行线, 这样的平行线( )
A.有且只有一条 B.不存在
C.不存在或只有一条 D.不存在或有无数条
9.(3分)如图,下列说法正确的是( )
A.因为∠1=∠3,所以EF∥GH B.因为∠1=∠2,所以AB∥CD
C.因为∠1=∠3,所以AB∥CD D.因为∠1=∠2,所以EF∥GH
10.(3分)如图,直线AB、CD交于点O,OT⊥AB于O,CE∥AB交CD于点C,若∠ECO=30°,则∠DOT等于( )
A.30° B.45° C.60° D.120°
二、填空题(共8题;共24分)
11.(3分)用一个a的值说明命题“若,则”是错误的,这个值可以是 .
12.(3分)如图,直线,相交于点O,,垂足为O.若,则的度数为 .
13.(3分)小戴和小魏分别到黑板上经过点A画直线m与直线n,并且使得m∥p,n∥p,则直线m与n分别必然重合,这是因为
14.(3分)如图, 直线 被第三条直线 所截. 若 , 则直线 的位置关系是
15.(3分)一杆古秤在称物时的状态如图所示,已知∠1=80°,则∠2的度数为 .
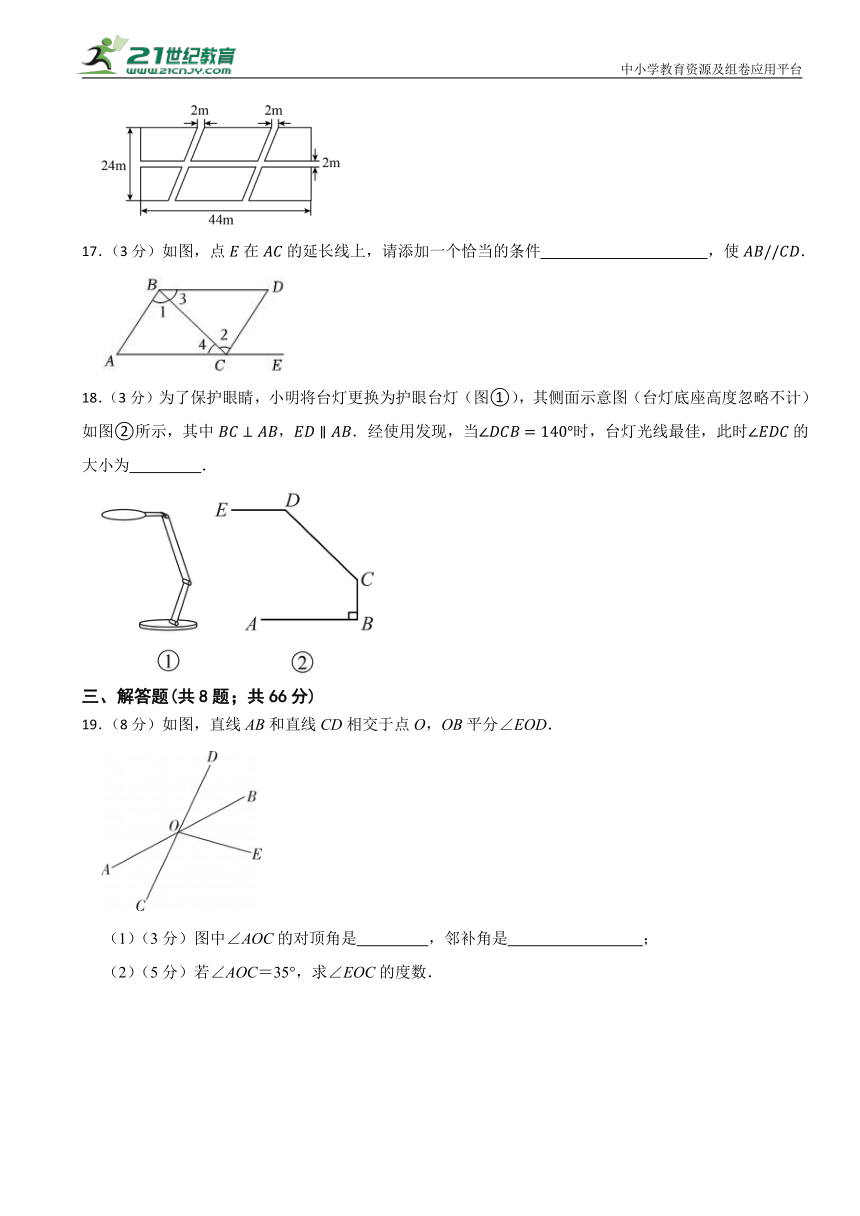
16.(3分)如图,有一块长为、宽为的长方形草坪,其中有三条直道将草坪分为六块,则六块草坪的面积和为 .
17.(3分)如图,点在的延长线上,请添加一个恰当的条件 ,使.
18.(3分)为了保护眼睛,小明将台灯更换为护眼台灯(图①),其侧面示意图(台灯底座高度忽略不计)如图②所示,其中,.经使用发现,当时,台灯光线最佳,此时的大小为 .
三、解答题(共8题;共66分)
19.(8分)如图,直线AB和直线CD相交于点O,OB平分∠EOD.
(1)(3分)图中∠AOC的对顶角是 ,邻补角是 ;
(2)(5分)若∠AOC=35°,求∠EOC的度数.
20.(8分)如图,已知1=3,2+3=180°,请说明AB与DE平行的理由.
21.(8分) 如图,,,试说明:AD∥BE.
补全下列推理过程,并在括号内填写推理依据.
∵,(已知)
∴∥________,(__________________________________)
∴________,(__________________________________)
又∵,(已知)
∴________,( _________________________________)
∴AD∥BE.(______________________________________)
22.(8分)如图,请你将△ABC平移,使得点A移动到点A′,并指出移动的距离.
23.(8分)如图, 直线 和 被 所截, 已知 , 求 的度数.
24.(8分)如图,∠AOB内有一点P:
(Ⅰ)过点P画PC∥OB交OA于C;
(Ⅱ)过点P画PD⊥OB于D;
(Ⅲ)连接OP,若OP是∠AOB的平分线,且∠AOB=60°,求∠AOP和∠CPO的度数.(直接写出答案即可)
25.(8分)如图,点E,F在分别在直线AB,CD上,∠AEF=70°,EM平分∠AEF交CD于点P,点N在直线CD上,且PN=PM,连接MN,若∠PMN=72.5°,判断直线AB与CD是否平行?并说明理由.
26.(10分)如图,在中,点D、F在边上,点E在边上,点G在边上,与的延长线交于点H,.
(1)(5分)判断和的位置关系,并说明理由;
(2)(5分)若,求的度数.
答案解析部分
1.【答案】B
【知识点】真命题与假命题
【解析】【解答】解:A、顺次连接对角线相等的四边形的四边中点所形成的图形是菱形,是真命题,不符合题意.
B、各边对应成比例的两个多边形相似;凸凹多边形各边成比例时,不是相似多边形,符合题意.
C、反比例函数的图象既是轴对轴图形,也是中心对称图形;是真命题,不符合题意.
D、已知二次函数,当时,y随x的增大而减小;是真命题,不符合题意.
故答案为:B
【分析】根据假命题的定义逐项判断即可。
2.【答案】A
【知识点】点到直线的距离
【解析】【解答】解:∵,,
∴点C到直线的距离是,
故选:A.
【分析】本题主要考查了点到直线的距离的定义,把直线外一点到直线的垂线段的长度,叫做点到直线的距离,据此定义得到点C到直线的距离即垂线段的长,即可解答.
3.【答案】A
【知识点】作图-平行线;尺规作图-作一个角等于已知角
【解析】【解答】解:根据作一个角等于已知角的步骤,结合平行线的判断定理,即可得解.
故答案为:A.
【分析】由平行线的判定定理,同位角相等,两直线平行,故需要作一个角等于已知角,从而根据根据作图痕迹判断即可得解.
4.【答案】B
【知识点】平行线的判定
【解析】【解答】解:∵∠2=∠5,
∴a∥b,
∵∠4=∠5,
∴a∥b,
∵∠1+∠5=180°,
∴a∥b,
故答案为:B.
【分析】根据平行线的判定定理逐项判断即可.
5.【答案】A
【知识点】角的运算;两直线平行,同位角相等
【解析】【解答】解:如图,记量角器所在圆的圆心为,过点作,
,
根据量角器的测量可知:,
∴估计的度数可能是45°,
故答案为:A.
【分析】记量角器所在圆的圆心为,过点作,由两直线平行,同位角相等得,然后利用角的度量即可得答案.
6.【答案】A
【知识点】平移的性质
【解析】【解答】由题意得:,的面积等于的面积,
又∵的面积为2,
∴的面积为2;
故答案为:A。
【分析】利用平移的性质得出 ,两个三角形高相等;可得出 的面积等于的面积进行解答即可。
7.【答案】C
【知识点】内错角的概念
【解析】【解答】解:∵,
∴,
∴A、B、D不符合题意,C符合题意;
故答案为:C.
【分析】利用两直线平行,同位角相等、内错角相等和同旁内角互补的性质分析求解即可.
8.【答案】C
【知识点】平行公理及推论
【解析】【解答】解:当点A在直线上时,过点A不能作直线 的平行线;
当点A不在直线上时,过点 作直线 的平行线有且只有一条;
故答案为:C.
【分析】分点A在直线上和直线外两种情况即可.
9.【答案】B
【知识点】平行线的判定
【解析】【解答】解:A、由∠1=∠3,因为∠1与∠3既不是同位角,也不是内错角,所以不能判定EF∥GH,故不符合题意;
B、 因为∠1=∠2,所以AB∥CD ,正确,故符合题意;
C、由∠1=∠3,因为∠1与∠3既不是同位角,也不是内错角,所以不能判定AB∥CD,故不符合题意;
D、 因为∠1=∠2,所以AB∥CD ,故不符合题意;
故答案为:B.
【分析】根据同位角相等两直线平行,内错角相等两直线平行,据此逐项判断即可.
10.【答案】C
【知识点】垂线的概念;两直线平行,同位角相等
【解析】【解答】解:∵,
∴(两直线平行,同位角相等)
∵
∴
∴
故答案为:C.
【分析】根据两直线平行,同位角相等得出,结合图即可求解.
11.【答案】(答案不唯一)
【知识点】真命题与假命题
【解析】【解答】解:当a=时,a2=,,而<2,
∴命题“若a>0,则a2>”是假命题,
故答案为:(答案不唯一).
【分析】举出一个符合条件的a值,而结论是错误的,据此解答即可.
12.【答案】
【知识点】垂线的概念;邻补角
【解析】【解答】解:∵,
∴,
∵,
∴,
∴,
故答案为:.
【分析】本题主要考查了垂直的定义、邻补角的性质,先求解,证得,得到,再利用角的和差关系,列出算式,即可得到答案.
13.【答案】过直线外一点,有且只有一条直线与已知直线平行
【知识点】平行公理及推论
【解析】【解答】解:∵直线m、n都经过点A,且m∥p,n∥p,
∴ 直线m与n分别必然重合 (过直线外一点,有且只有一条直线与已知直线平行).
故答案为:过直线外一点,有且只有一条直线与已知直线平行.
【分析】根据直线公理:过直线外一点,有且只有一条直线与已知直线平行可得答案.
14.【答案】平行
【知识点】平行线的判定;邻补角
【解析】【解答】解:∵∠2=130°,
∴∠3=180°-∠2=50°,
∵∠1=50°,
∴∠1=∠3,
∴a∥b(同位角相等,两直线平行).
故答案为:平行.
【分析】根据∠2与∠3是邻补角,利用已知即可求出∠3=50°,从而得∠1=∠3,利用同位角相等,两直线平行即可得出a,b的位置关系.
15.【答案】100°
【知识点】两直线平行,内错角相等
【解析】【解答】解:由题意可得如图所示,
∵,,
∴,
由题意可知,,
,
故答案:.
【分析】先由邻补角求出∠3的度数,再由平行线的性质求∠2的度数.
16.【答案】880
【知识点】平移的性质;有理数混合运算的实际应用
【解析】【解答】解:∵长方形的对边平行,根据平行线间的距离处处相等,
∴两个平行四边形直道长和高转换成等底等高的长方形时,面积不变,故将三条直道平移到长方形一边时,如图所示:面积保持不变.
∴六块草坪的面积(44-2×2)(24-2)=880(m2).
故答案为:880.
【分析】根据长方形的对边平行以及平行线之间的距离处处相等,将三条直道平移到长方形一边时,得到一块完整的长方形,再计算面积即可.
17.【答案】答案不唯一
【知识点】平行线的判定
【解析】【解答】解:∵∠1、∠2为AB与CD的内错角,
∴当∠1=∠2时,AB∥CD,
故答案为:∠1=∠2(答案不唯一).
【分析】利用平行线的判定定理添加条件即可.
18.【答案】
【知识点】平行线的性质
【解析】【解答】解:如图所示,过点作,
∵,∴,
,,,
,,
∵,,
.
故答案为:.
【分析】本题考查平行线的性质与判定及其应用,过作,得到,由,得到,结合,求出,在由平行线的性质,得到,即可求的的度数,得到答案.
19.【答案】(1)∠BOD;∠AOD,∠BOC
(2)解:∵OB平分∠EOD,
∴∠DOE=2∠BOD,
∵∠BOD=∠AOC=35°,
∴∠DOE=2×35°=70°,
∵∠EOC+∠DOE=180°,
∴∠EOC=180°-∠DOE=110°
【知识点】对顶角及其性质;邻补角
【解析】【分析】(1)根据对顶角定义:如果一个角的两边分别是另一个角两边的反向延长线,且这两个角有公共顶点,那么这两个角是对顶角,由此可找到 ∠AOC的对顶角是 ∠BOD ,由邻补角定义:两个角有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,叫作互为邻补角,可知 ∠AOC的邻补角是 ∠AOD,∠BOC;
(2)先根据对顶角求出∠DOB=35°,在根据条件OB平分∠EOD,∠BOE=35°,则∠DOE=70°,在根据平角性质,最后求出∠DOE=110°。
20.【答案】解:∵∠2+∠4=180°,∠2+∠3=180°,
∴∠3=∠4,
∵∠1=∠3,
∴∠1=∠4,
∴AB∥DE.
【知识点】平行线的判定;邻补角
【解析】【分析】根据邻补角的性质可得∠2+∠4=180°,推出∠3=∠4,最终得到∠1=∠4,根据平行线的判定即可求得.
21.【答案】解:如图,,,试说明:.
补全下列推理过程,并在括号内填写推理依据.
因为,(已知)
所以______,(_内错角相等,两直线平行;_____)
所以______,(_两直线平行,内错角相等_____)
又因为,(已知)
所以______,(等量代换)
所以.(__内错角相等,两直线平行____)
【知识点】平行线的判定;平行线的性质
【解析】【分析】根据平行线的性质和平行线的判定即可解题.
22.【答案】解:如图所示:△A′B′C′即为所求,
平移的距离为: =4 .
【知识点】作图﹣平移
【解析】【分析】根据平移的性质结合A点平移的距离得出B,C平移的后的位置,进而得出答案.
23.【答案】解:∵∠1=2∠2,∠2=2∠3,∠1+∠3=180°,
∴设∠3=x°,则∠2=2x°,∠1=4x°,
∴x+4x=180,
解得:x=36,∠4=∠2=2x°=72°,
∴∠4的度数为72°.
【知识点】对顶角及其性质;邻补角
【解析】【分析】根据∠1=2∠2,∠2=2∠3,设∠3=x°,则∠2=2x°,∠1=4x°,根据平角的定义得x+4x=180,解得x的值,最后根据对顶角的性质即可求解.
24.【答案】解:(Ⅰ)如图,直线PC即为所求作.
(Ⅱ)如图,线段PD即为所求作.
(Ⅲ)∵∠AOB=60°,OP平分∠AOB,
∴∠AOP=∠POD=30°,
∵PC∥OD,
∴∠CPO=∠POD=30°.
【知识点】作图-平行线;尺规作图-垂线
【解析】【分析】(Ⅰ)过点P作PC//OB交OA于点C;
(Ⅱ)过点P作PD垂直OB于D;
(Ⅲ)利用角平分线的定义,角平分线的性质求解即可。
25.【答案】解: AB//CD,
理由:∵PN=PM,∠PMN=72.5°,
∴∠PNM=∠PMN=72.5°,
∴∠MPN=35°,
∴∠EPF=∠MPN=35°,
∵EM平分∠AEF,
∴∠AEM=∠AEF=35°,
∴∠AEM=∠EPF,
∴AB//CD.
【知识点】平行线的判定
【解析】【分析】先利用等边对等角的性质和三角形的内角和求出∠MPN=35°,再利用角平分线的定义可得∠AEM=∠AEF=35°,因此∠AEM=∠EPF,从而得到AB//CD。
26.【答案】(1)证明:.理由如下:如图所示,
,
,
,
又,
,
.
(2)解:如图所示,
由(1)得,
,
,
,
又∵∠4=28°
,
∴∠2=∠5=32°
又,
.
【知识点】平行线的判定与性质
【解析】【分析】(1)由,可推出,继而得到,在根据条件∠2+∠3=180°,等量代换得到,即可证明位置关系;
(2)由(1)中结论及题目条件,推出,继而求出,再根据得出.
冀教版七年级数学下册 第七章 相交线与平行线 单元测试题(2024)
一、选择题(共10题;共30分)
1.(3分)下列命题中,假命题的是( ).
A.顺次连接对角线相等的四边形的四边中点所形成的图形是菱形;
B.各边对应成比例的两个多边形相似;
C.反比例函数的图象既是轴对轴图形,也是中心对称图形;
D.已知二次函数,当时,y随x的增大而减小.
2.(3分)如图,三角形ABC中,,于点D,若,则点C到直线AB的距离是( )
A. B.3 C.4 D.5
3.(3分)下面四个图是小明用尺规过点C作AB边的平行线所留下的作图痕迹,其中正确的是( )
A. B.
C. D.
4.(3分)如图,直线a,b被直线c所截,下列条件中,不能判定a∥b的是( )
A.∠2=∠5 B.∠1=∠3
C.∠5=∠4 D.∠1+∠5=180°
5.(3分)如图,鸿鸿同学在使用量角器时操作不规范,请你根据她的测量图估计的度数可能是( )
A. B. C. D.
6.(3分)如图,将沿射线方向移动,使点移动到点,得到,连接,若的面积为2,则的面积为( )
A.2 B.4 C.6 D.16
7.(3分)如图,,则下列结论正确的是( )
A. B. C. D.
8.(3分) 过点 作直线 的平行线, 这样的平行线( )
A.有且只有一条 B.不存在
C.不存在或只有一条 D.不存在或有无数条
9.(3分)如图,下列说法正确的是( )
A.因为∠1=∠3,所以EF∥GH B.因为∠1=∠2,所以AB∥CD
C.因为∠1=∠3,所以AB∥CD D.因为∠1=∠2,所以EF∥GH
10.(3分)如图,直线AB、CD交于点O,OT⊥AB于O,CE∥AB交CD于点C,若∠ECO=30°,则∠DOT等于( )
A.30° B.45° C.60° D.120°
二、填空题(共8题;共24分)
11.(3分)用一个a的值说明命题“若,则”是错误的,这个值可以是 .
12.(3分)如图,直线,相交于点O,,垂足为O.若,则的度数为 .
13.(3分)小戴和小魏分别到黑板上经过点A画直线m与直线n,并且使得m∥p,n∥p,则直线m与n分别必然重合,这是因为
14.(3分)如图, 直线 被第三条直线 所截. 若 , 则直线 的位置关系是
15.(3分)一杆古秤在称物时的状态如图所示,已知∠1=80°,则∠2的度数为 .
16.(3分)如图,有一块长为、宽为的长方形草坪,其中有三条直道将草坪分为六块,则六块草坪的面积和为 .
17.(3分)如图,点在的延长线上,请添加一个恰当的条件 ,使.
18.(3分)为了保护眼睛,小明将台灯更换为护眼台灯(图①),其侧面示意图(台灯底座高度忽略不计)如图②所示,其中,.经使用发现,当时,台灯光线最佳,此时的大小为 .
三、解答题(共8题;共66分)
19.(8分)如图,直线AB和直线CD相交于点O,OB平分∠EOD.
(1)(3分)图中∠AOC的对顶角是 ,邻补角是 ;
(2)(5分)若∠AOC=35°,求∠EOC的度数.
20.(8分)如图,已知1=3,2+3=180°,请说明AB与DE平行的理由.
21.(8分) 如图,,,试说明:AD∥BE.
补全下列推理过程,并在括号内填写推理依据.
∵,(已知)
∴∥________,(__________________________________)
∴________,(__________________________________)
又∵,(已知)
∴________,( _________________________________)
∴AD∥BE.(______________________________________)
22.(8分)如图,请你将△ABC平移,使得点A移动到点A′,并指出移动的距离.
23.(8分)如图, 直线 和 被 所截, 已知 , 求 的度数.
24.(8分)如图,∠AOB内有一点P:
(Ⅰ)过点P画PC∥OB交OA于C;
(Ⅱ)过点P画PD⊥OB于D;
(Ⅲ)连接OP,若OP是∠AOB的平分线,且∠AOB=60°,求∠AOP和∠CPO的度数.(直接写出答案即可)
25.(8分)如图,点E,F在分别在直线AB,CD上,∠AEF=70°,EM平分∠AEF交CD于点P,点N在直线CD上,且PN=PM,连接MN,若∠PMN=72.5°,判断直线AB与CD是否平行?并说明理由.
26.(10分)如图,在中,点D、F在边上,点E在边上,点G在边上,与的延长线交于点H,.
(1)(5分)判断和的位置关系,并说明理由;
(2)(5分)若,求的度数.
答案解析部分
1.【答案】B
【知识点】真命题与假命题
【解析】【解答】解:A、顺次连接对角线相等的四边形的四边中点所形成的图形是菱形,是真命题,不符合题意.
B、各边对应成比例的两个多边形相似;凸凹多边形各边成比例时,不是相似多边形,符合题意.
C、反比例函数的图象既是轴对轴图形,也是中心对称图形;是真命题,不符合题意.
D、已知二次函数,当时,y随x的增大而减小;是真命题,不符合题意.
故答案为:B
【分析】根据假命题的定义逐项判断即可。
2.【答案】A
【知识点】点到直线的距离
【解析】【解答】解:∵,,
∴点C到直线的距离是,
故选:A.
【分析】本题主要考查了点到直线的距离的定义,把直线外一点到直线的垂线段的长度,叫做点到直线的距离,据此定义得到点C到直线的距离即垂线段的长,即可解答.
3.【答案】A
【知识点】作图-平行线;尺规作图-作一个角等于已知角
【解析】【解答】解:根据作一个角等于已知角的步骤,结合平行线的判断定理,即可得解.
故答案为:A.
【分析】由平行线的判定定理,同位角相等,两直线平行,故需要作一个角等于已知角,从而根据根据作图痕迹判断即可得解.
4.【答案】B
【知识点】平行线的判定
【解析】【解答】解:∵∠2=∠5,
∴a∥b,
∵∠4=∠5,
∴a∥b,
∵∠1+∠5=180°,
∴a∥b,
故答案为:B.
【分析】根据平行线的判定定理逐项判断即可.
5.【答案】A
【知识点】角的运算;两直线平行,同位角相等
【解析】【解答】解:如图,记量角器所在圆的圆心为,过点作,
,
根据量角器的测量可知:,
∴估计的度数可能是45°,
故答案为:A.
【分析】记量角器所在圆的圆心为,过点作,由两直线平行,同位角相等得,然后利用角的度量即可得答案.
6.【答案】A
【知识点】平移的性质
【解析】【解答】由题意得:,的面积等于的面积,
又∵的面积为2,
∴的面积为2;
故答案为:A。
【分析】利用平移的性质得出 ,两个三角形高相等;可得出 的面积等于的面积进行解答即可。
7.【答案】C
【知识点】内错角的概念
【解析】【解答】解:∵,
∴,
∴A、B、D不符合题意,C符合题意;
故答案为:C.
【分析】利用两直线平行,同位角相等、内错角相等和同旁内角互补的性质分析求解即可.
8.【答案】C
【知识点】平行公理及推论
【解析】【解答】解:当点A在直线上时,过点A不能作直线 的平行线;
当点A不在直线上时,过点 作直线 的平行线有且只有一条;
故答案为:C.
【分析】分点A在直线上和直线外两种情况即可.
9.【答案】B
【知识点】平行线的判定
【解析】【解答】解:A、由∠1=∠3,因为∠1与∠3既不是同位角,也不是内错角,所以不能判定EF∥GH,故不符合题意;
B、 因为∠1=∠2,所以AB∥CD ,正确,故符合题意;
C、由∠1=∠3,因为∠1与∠3既不是同位角,也不是内错角,所以不能判定AB∥CD,故不符合题意;
D、 因为∠1=∠2,所以AB∥CD ,故不符合题意;
故答案为:B.
【分析】根据同位角相等两直线平行,内错角相等两直线平行,据此逐项判断即可.
10.【答案】C
【知识点】垂线的概念;两直线平行,同位角相等
【解析】【解答】解:∵,
∴(两直线平行,同位角相等)
∵
∴
∴
故答案为:C.
【分析】根据两直线平行,同位角相等得出,结合图即可求解.
11.【答案】(答案不唯一)
【知识点】真命题与假命题
【解析】【解答】解:当a=时,a2=,,而<2,
∴命题“若a>0,则a2>”是假命题,
故答案为:(答案不唯一).
【分析】举出一个符合条件的a值,而结论是错误的,据此解答即可.
12.【答案】
【知识点】垂线的概念;邻补角
【解析】【解答】解:∵,
∴,
∵,
∴,
∴,
故答案为:.
【分析】本题主要考查了垂直的定义、邻补角的性质,先求解,证得,得到,再利用角的和差关系,列出算式,即可得到答案.
13.【答案】过直线外一点,有且只有一条直线与已知直线平行
【知识点】平行公理及推论
【解析】【解答】解:∵直线m、n都经过点A,且m∥p,n∥p,
∴ 直线m与n分别必然重合 (过直线外一点,有且只有一条直线与已知直线平行).
故答案为:过直线外一点,有且只有一条直线与已知直线平行.
【分析】根据直线公理:过直线外一点,有且只有一条直线与已知直线平行可得答案.
14.【答案】平行
【知识点】平行线的判定;邻补角
【解析】【解答】解:∵∠2=130°,
∴∠3=180°-∠2=50°,
∵∠1=50°,
∴∠1=∠3,
∴a∥b(同位角相等,两直线平行).
故答案为:平行.
【分析】根据∠2与∠3是邻补角,利用已知即可求出∠3=50°,从而得∠1=∠3,利用同位角相等,两直线平行即可得出a,b的位置关系.
15.【答案】100°
【知识点】两直线平行,内错角相等
【解析】【解答】解:由题意可得如图所示,
∵,,
∴,
由题意可知,,
,
故答案:.
【分析】先由邻补角求出∠3的度数,再由平行线的性质求∠2的度数.
16.【答案】880
【知识点】平移的性质;有理数混合运算的实际应用
【解析】【解答】解:∵长方形的对边平行,根据平行线间的距离处处相等,
∴两个平行四边形直道长和高转换成等底等高的长方形时,面积不变,故将三条直道平移到长方形一边时,如图所示:面积保持不变.
∴六块草坪的面积(44-2×2)(24-2)=880(m2).
故答案为:880.
【分析】根据长方形的对边平行以及平行线之间的距离处处相等,将三条直道平移到长方形一边时,得到一块完整的长方形,再计算面积即可.
17.【答案】答案不唯一
【知识点】平行线的判定
【解析】【解答】解:∵∠1、∠2为AB与CD的内错角,
∴当∠1=∠2时,AB∥CD,
故答案为:∠1=∠2(答案不唯一).
【分析】利用平行线的判定定理添加条件即可.
18.【答案】
【知识点】平行线的性质
【解析】【解答】解:如图所示,过点作,
∵,∴,
,,,
,,
∵,,
.
故答案为:.
【分析】本题考查平行线的性质与判定及其应用,过作,得到,由,得到,结合,求出,在由平行线的性质,得到,即可求的的度数,得到答案.
19.【答案】(1)∠BOD;∠AOD,∠BOC
(2)解:∵OB平分∠EOD,
∴∠DOE=2∠BOD,
∵∠BOD=∠AOC=35°,
∴∠DOE=2×35°=70°,
∵∠EOC+∠DOE=180°,
∴∠EOC=180°-∠DOE=110°
【知识点】对顶角及其性质;邻补角
【解析】【分析】(1)根据对顶角定义:如果一个角的两边分别是另一个角两边的反向延长线,且这两个角有公共顶点,那么这两个角是对顶角,由此可找到 ∠AOC的对顶角是 ∠BOD ,由邻补角定义:两个角有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,叫作互为邻补角,可知 ∠AOC的邻补角是 ∠AOD,∠BOC;
(2)先根据对顶角求出∠DOB=35°,在根据条件OB平分∠EOD,∠BOE=35°,则∠DOE=70°,在根据平角性质,最后求出∠DOE=110°。
20.【答案】解:∵∠2+∠4=180°,∠2+∠3=180°,
∴∠3=∠4,
∵∠1=∠3,
∴∠1=∠4,
∴AB∥DE.
【知识点】平行线的判定;邻补角
【解析】【分析】根据邻补角的性质可得∠2+∠4=180°,推出∠3=∠4,最终得到∠1=∠4,根据平行线的判定即可求得.
21.【答案】解:如图,,,试说明:.
补全下列推理过程,并在括号内填写推理依据.
因为,(已知)
所以______,(_内错角相等,两直线平行;_____)
所以______,(_两直线平行,内错角相等_____)
又因为,(已知)
所以______,(等量代换)
所以.(__内错角相等,两直线平行____)
【知识点】平行线的判定;平行线的性质
【解析】【分析】根据平行线的性质和平行线的判定即可解题.
22.【答案】解:如图所示:△A′B′C′即为所求,
平移的距离为: =4 .
【知识点】作图﹣平移
【解析】【分析】根据平移的性质结合A点平移的距离得出B,C平移的后的位置,进而得出答案.
23.【答案】解:∵∠1=2∠2,∠2=2∠3,∠1+∠3=180°,
∴设∠3=x°,则∠2=2x°,∠1=4x°,
∴x+4x=180,
解得:x=36,∠4=∠2=2x°=72°,
∴∠4的度数为72°.
【知识点】对顶角及其性质;邻补角
【解析】【分析】根据∠1=2∠2,∠2=2∠3,设∠3=x°,则∠2=2x°,∠1=4x°,根据平角的定义得x+4x=180,解得x的值,最后根据对顶角的性质即可求解.
24.【答案】解:(Ⅰ)如图,直线PC即为所求作.
(Ⅱ)如图,线段PD即为所求作.
(Ⅲ)∵∠AOB=60°,OP平分∠AOB,
∴∠AOP=∠POD=30°,
∵PC∥OD,
∴∠CPO=∠POD=30°.
【知识点】作图-平行线;尺规作图-垂线
【解析】【分析】(Ⅰ)过点P作PC//OB交OA于点C;
(Ⅱ)过点P作PD垂直OB于D;
(Ⅲ)利用角平分线的定义,角平分线的性质求解即可。
25.【答案】解: AB//CD,
理由:∵PN=PM,∠PMN=72.5°,
∴∠PNM=∠PMN=72.5°,
∴∠MPN=35°,
∴∠EPF=∠MPN=35°,
∵EM平分∠AEF,
∴∠AEM=∠AEF=35°,
∴∠AEM=∠EPF,
∴AB//CD.
【知识点】平行线的判定
【解析】【分析】先利用等边对等角的性质和三角形的内角和求出∠MPN=35°,再利用角平分线的定义可得∠AEM=∠AEF=35°,因此∠AEM=∠EPF,从而得到AB//CD。
26.【答案】(1)证明:.理由如下:如图所示,
,
,
,
又,
,
.
(2)解:如图所示,
由(1)得,
,
,
,
又∵∠4=28°
,
∴∠2=∠5=32°
又,
.
【知识点】平行线的判定与性质
【解析】【分析】(1)由,可推出,继而得到,在根据条件∠2+∠3=180°,等量代换得到,即可证明位置关系;
(2)由(1)中结论及题目条件,推出,继而求出,再根据得出.
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
