直线与圆位置关系公开教学课件(共21张PPT)
文档属性
| 名称 | 直线与圆位置关系公开教学课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 254.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-09 00:00:00 | ||
图片预览







文档简介
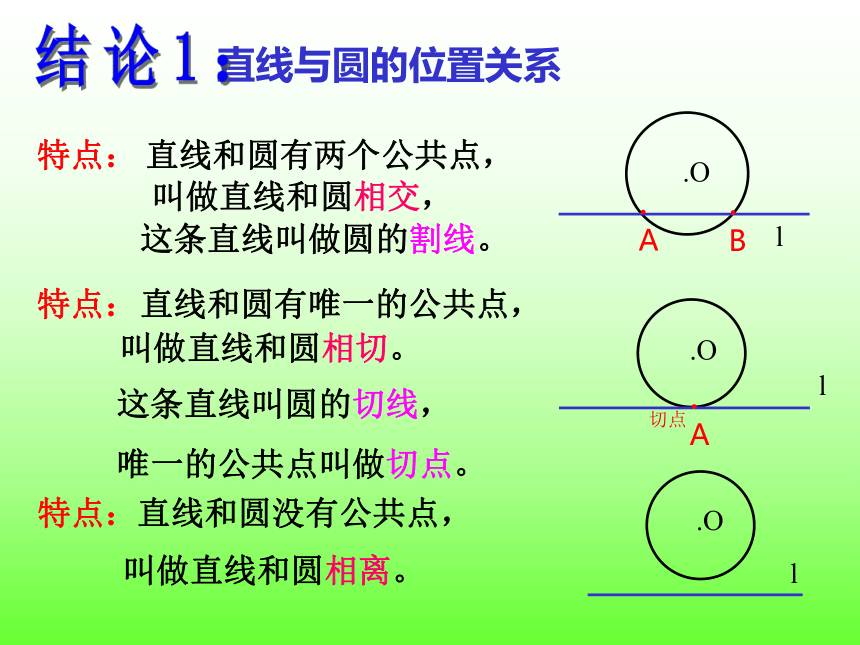
课件21张PPT。直线与圆的位置关系第24章24.2.2五指山思源实验学校 黄文强复习回顾一、点与圆的位置关系d:点到圆心的距离; r:圆的半径点p在圆外 d>r点p在圆上 d=r点p在圆内 d 唯一的公共点叫做切点。.Ol特点:直线和圆有两个公共点,叫做直线和圆相交,这条直线叫做圆的割线。 直线与圆的位置关系 .A.A.B切点结论1:结论2: 直线与圆的位置关系的判定方法1 直线和圆有两个公共点相交直线和圆只有一个公共点相切直线和圆没有公共点相离三、课堂练习 1、你能举出生活中直线与圆相交、相切、相离的实例吗?太阳与海平面的位置关系,
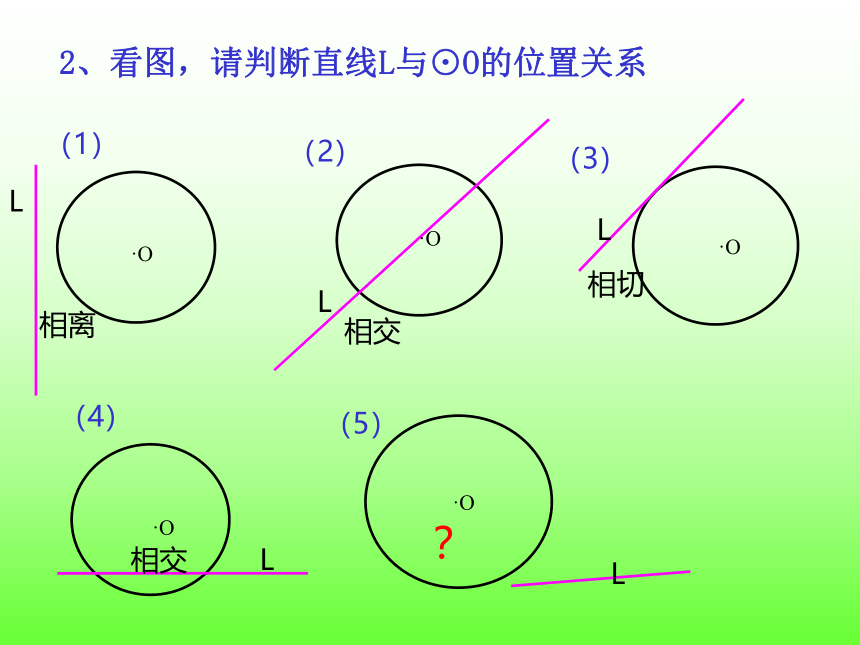
自行车的车轮与地面之间的位置关系,都给我们直线和圆的位置关系的印象。地面2、看图,请判断直线L与⊙O的位置关系(1)(2)(3)(4)(5)相离相切相交相交?LLLLL·O·O·O·O·O(5)?l 如果,公共点的个数不好判断,该怎么办?·O “直线和圆的位置关系”能否像“点和圆的位置关系”一样进行数量分析呢?·
A·
B四、自主学习2 画出直线L与圆O的三种位置关系图,并作出圆心o到直线L的距离,其大小用字母d来表示,圆的半径用字母r表示。相交相切相离2、直线和圆相切d = r3、直线和圆相交d < r1、直线和圆相离d > r结论1:直线与圆的性质结论2:直线与圆的位置关系的判定方法2d > r直线和圆相离d = r直线和圆相切直线和圆相交d < r五、课堂练习1、已知圆的半径r=7cm,圆心与直线的距离为dcm,
当d=6cm时,直线与圆的位置关系是_________。
当d=7cm时,直线与圆的位置关系是_________。
当d=8cm时,直线与圆的位置关系是_________。五、课堂练习2、已知圆心与直线的距离为5cm,圆的半径为r,
当r=9cm时,直线与圆的位置关系是_________。
当r=5cm时,直线与圆的位置关系是_________。
当d=1cm时,直线与圆的位置关系是_________。五、课堂练习3、已知圆与直线相交,圆的半径为4,则d的取值范围是( )
A d<4 B d>4 C d≥4 D d=4
4、已知圆与直线相切,圆的半径为4,则d的取值范围是______________。
5、已知圆与直线相离,圆的半径为4,则d的取值范围是______________。
五、课堂练习6、已知圆与直线相交,圆心到直线的距离为5,则圆的半径的取值范围是( )
A r<5 B r>5 C r≥5 D r=5
7、已知圆与直线相切,圆心到直线的距离为5,则圆的半径的取值范围是_________。
8、已知圆与直线相离,圆心到直线的距离为5,则圆的半径的取值范围是_________。0d>r1d=r切点切线2d1.⊙O的半径为3 ,圆O与直线L没有公共点,则它们的关系是( )
A.相离 B.相交 C.相切 D.无法确定
2.圆心O到直线的距离等于⊙O的半径,则直线和⊙O的位置关系是( )
A.相离 B.相交 C.相切 D.相切或相交
3.AC七、当堂检测
4.⊙O的半径为3 ,圆心O到直线L的距离为d,若直线L
与⊙O没有公共点,则d为( ):
A.d >3 B.d<3 C.d ≤3 D.d =3
5.圆心O到直线的距离等于5,它们只有一个公共点,则⊙O的半径是( )
A.4 B.5 C.6 D.无法确定
3.判断:如果直线和圆相切,则该直线和圆一定有一个公共点.( )AB√七、当堂检测同步练习册P58:直线与圆的位置关系(一) 作业
自行车的车轮与地面之间的位置关系,都给我们直线和圆的位置关系的印象。地面2、看图,请判断直线L与⊙O的位置关系(1)(2)(3)(4)(5)相离相切相交相交?LLLLL·O·O·O·O·O(5)?l 如果,公共点的个数不好判断,该怎么办?·O “直线和圆的位置关系”能否像“点和圆的位置关系”一样进行数量分析呢?·
A·
B四、自主学习2 画出直线L与圆O的三种位置关系图,并作出圆心o到直线L的距离,其大小用字母d来表示,圆的半径用字母r表示。相交相切相离2、直线和圆相切d = r3、直线和圆相交d < r1、直线和圆相离d > r结论1:直线与圆的性质结论2:直线与圆的位置关系的判定方法2d > r直线和圆相离d = r直线和圆相切直线和圆相交d < r五、课堂练习1、已知圆的半径r=7cm,圆心与直线的距离为dcm,
当d=6cm时,直线与圆的位置关系是_________。
当d=7cm时,直线与圆的位置关系是_________。
当d=8cm时,直线与圆的位置关系是_________。五、课堂练习2、已知圆心与直线的距离为5cm,圆的半径为r,
当r=9cm时,直线与圆的位置关系是_________。
当r=5cm时,直线与圆的位置关系是_________。
当d=1cm时,直线与圆的位置关系是_________。五、课堂练习3、已知圆与直线相交,圆的半径为4,则d的取值范围是( )
A d<4 B d>4 C d≥4 D d=4
4、已知圆与直线相切,圆的半径为4,则d的取值范围是______________。
5、已知圆与直线相离,圆的半径为4,则d的取值范围是______________。
五、课堂练习6、已知圆与直线相交,圆心到直线的距离为5,则圆的半径的取值范围是( )
A r<5 B r>5 C r≥5 D r=5
7、已知圆与直线相切,圆心到直线的距离为5,则圆的半径的取值范围是_________。
8、已知圆与直线相离,圆心到直线的距离为5,则圆的半径的取值范围是_________。0d>r1d=r切点切线2d
A.相离 B.相交 C.相切 D.无法确定
2.圆心O到直线的距离等于⊙O的半径,则直线和⊙O的位置关系是( )
A.相离 B.相交 C.相切 D.相切或相交
3.AC七、当堂检测
4.⊙O的半径为3 ,圆心O到直线L的距离为d,若直线L
与⊙O没有公共点,则d为( ):
A.d >3 B.d<3 C.d ≤3 D.d =3
5.圆心O到直线的距离等于5,它们只有一个公共点,则⊙O的半径是( )
A.4 B.5 C.6 D.无法确定
3.判断:如果直线和圆相切,则该直线和圆一定有一个公共点.( )AB√七、当堂检测同步练习册P58:直线与圆的位置关系(一) 作业
