第二十章 数据的分析 章末小结与提升(含答案) 2024-2025学年人教版初中数学八年级下册
文档属性
| 名称 | 第二十章 数据的分析 章末小结与提升(含答案) 2024-2025学年人教版初中数学八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 257.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-03 20:38:45 | ||
图片预览



文档简介
第二十章 数据的分析 章末小结与提升
◆必记公式 1.算式平均数公式:=(x1+x2+…+xn). 2.加权平均数公式:=(其中f1+f2+…+fk=n). 3.方差公式:s2=[(x1-)2+(x2-)2+…+(xn-)2].
【专题提升】
1.一组数据-2,5,3,7,增加一个数据后,众数为7,则增加数据后中位数是 ()
A.5 B.3 C.4 D.7
2.在电脑上,为了让使用者直观地看出磁盘“已用空间”与“可用空间”占“整个磁盘空间”的百分比,使用的统计图应该是 ()
A.条形统计图 B.扇形统计图
C.折线统计图 D.以上都可以
3.一次测试中,五名同学的得分分别为60,85,50,60,90,后经过校对发现,得90分的同学应得85分,校对后的五个数据与之前五个数据相比,集中趋势不变的是 ()
A.只有中位数 B.只有平均数
C.只有众数 D.中位数与众数
4.【2024·河南中考】2024年3月是第8个全国近视防控宣传教育月,其主题是“有效减少近视发生,共同守护光明未来”.某校组织各班围绕这个主题开展板报宣传活动,并对各班的宣传板报进行评分,得分情况如图,则得分的众数为 分.
5.如图,投壶是中国古代一种传统礼仪和宴饮游戏.在一次投壶比赛中,甲、乙两人成绩的平均数分别为,,方差分别为,.若=,=2.3,=1.2,则成绩更稳定的是 (填“甲”或“乙”).
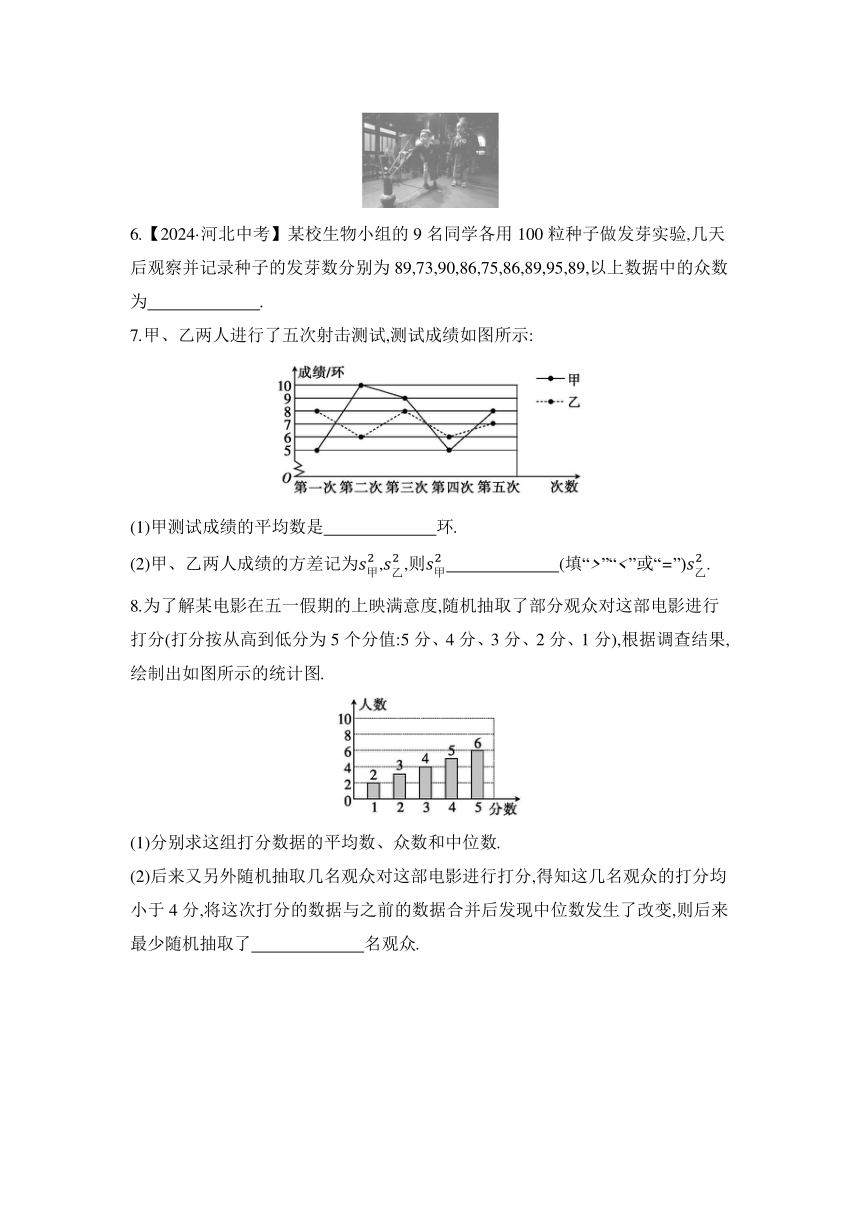
6.【2024·河北中考】某校生物小组的9名同学各用100粒种子做发芽实验,几天后观察并记录种子的发芽数分别为89,73,90,86,75,86,89,95,89,以上数据中的众数为 .
7.甲、乙两人进行了五次射击测试,测试成绩如图所示:
(1)甲测试成绩的平均数是 环.
(2)甲、乙两人成绩的方差记为,,则 (填“>”“<”或“=”).
8.为了解某电影在五一假期的上映满意度,随机抽取了部分观众对这部电影进行打分(打分按从高到低分为5个分值:5分、4分、3分、2分、1分),根据调查结果,绘制出如图所示的统计图.
(1)分别求这组打分数据的平均数、众数和中位数.
(2)后来又另外随机抽取几名观众对这部电影进行打分,得知这几名观众的打分均小于4分,将这次打分的数据与之前的数据合并后发现中位数发生了改变,则后来最少随机抽取了 名观众.
9. 为激发青少年崇尚科学、探索未知的热情,学校开展“科学小博士”知识竞赛.各班以小组为单位组织初赛,规定满分为10分、9分及以上为优秀.
数据整理:小夏将本班甲、乙两组同学(每组8人)初赛的成绩整理成如下的统计图.
数据分析:小夏对这两个小组的成绩进行了如下分析.
平均数/分 中位数/分 众数/分 方差 优秀率
甲组 7.625 a 7 4.48 37.5%
乙组 7.625 7 b 0.73 c
请认真阅读上述信息,回答下列问题:
(1)填空:a= ,b= ,c= .
(2)小祺认为甲、乙两组成绩的平均数相等,因此两个组成绩一样好.小夏认为小祺的观点比较片面,请结合上表中的信息帮小夏说明理由(写出两条即可).
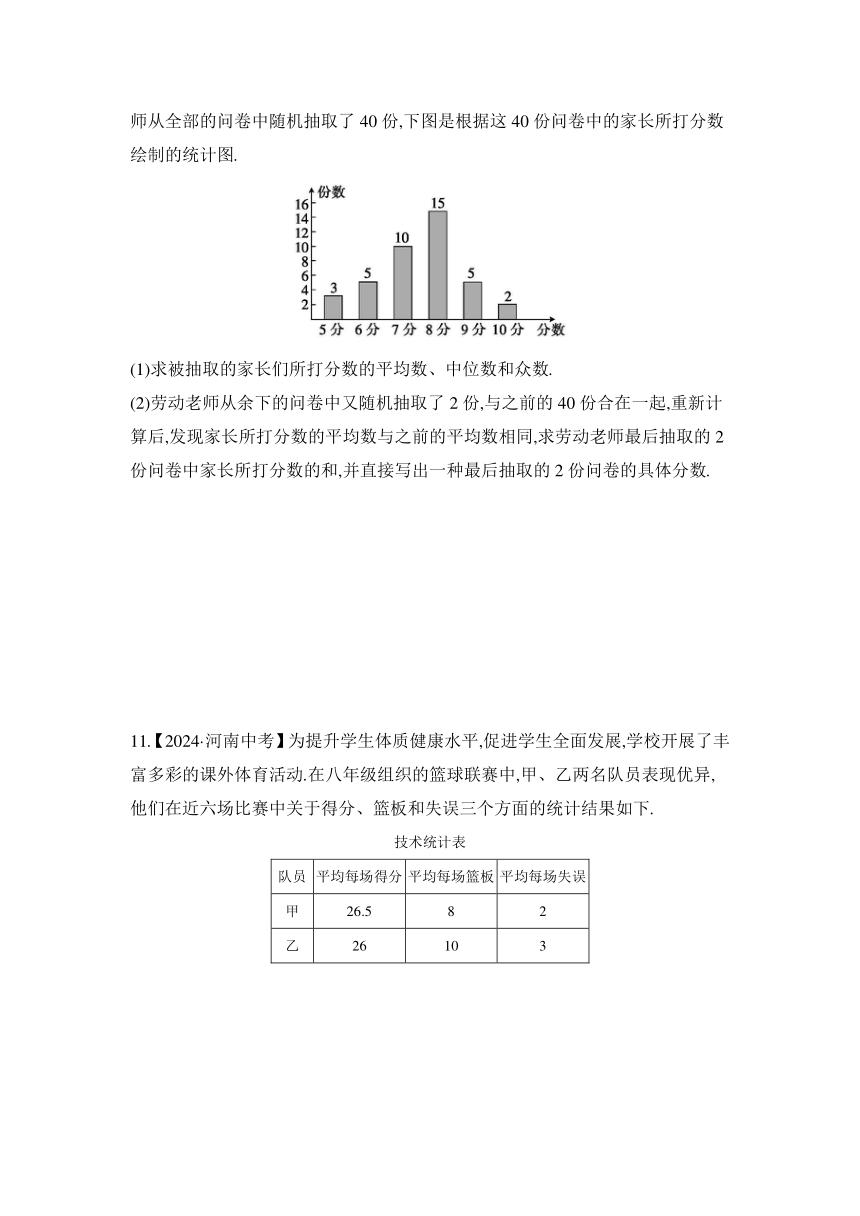
10.某校为了解学生校外的劳动表现,对全校学生进行了问卷调查,让每位学生的家长对自家孩子打分,分数为5分、6分、7分、8分、9分、10分,共6档.劳动老师从全部的问卷中随机抽取了40份,下图是根据这40份问卷中的家长所打分数绘制的统计图.
(1)求被抽取的家长们所打分数的平均数、中位数和众数.
(2)劳动老师从余下的问卷中又随机抽取了2份,与之前的40份合在一起,重新计算后,发现家长所打分数的平均数与之前的平均数相同,求劳动老师最后抽取的2份问卷中家长所打分数的和,并直接写出一种最后抽取的2份问卷的具体分数.
11.【2024·河南中考】为提升学生体质健康水平,促进学生全面发展,学校开展了丰富多彩的课外体育活动.在八年级组织的篮球联赛中,甲、乙两名队员表现优异,他们在近六场比赛中关于得分、篮板和失误三个方面的统计结果如下.
技术统计表
队员 平均每场得分 平均每场篮板 平均每场失误
甲 26.5 8 2
乙 26 10 3
根据以上信息,回答下列问题:
(1)这六场比赛中,得分更稳定的队员是 (填“甲”或“乙”);甲队员得分的中位数为27.5分,乙队员得分的中位数为 分.
(2)请从得分方面分析:这六场比赛中,甲、乙两名队员谁的表现更好.
(3)规定“综合得分”为平均每场得分×1+平均每场篮板×1.5+平均每场失误×(-1),且综合得分越高表现越好.请利用这种评价方法,比较这六场比赛中甲、乙两名队员谁的表现更好.
小情境主题:安全第一
12.环球网消息称:近年来的电动自行车火灾事故80%都是在充电时发生的,超过一半的电动自行车火灾发生在夜间充电的过程中.为了规避风险,某校政教处对学生进行规范充电培训活动,并对培训效果按10分制进行检测评分.为了解这次培训的效果,现从各年级随机抽取男、女生各10名的检测成绩作为样本进行整理,并绘制成如下不完整的统计图表:
抽取的10名女生检测成绩统计表
成绩/分 6 7 8 9 10
人数 1 2 m 3 n
注:10名女生检测成绩的中位数为8.5分.
抽取的10名男生检测成绩扇形图
请根据以上信息,回答下列问题:
(1)样本中男生检测成绩为10分的学生数是 ,众数为 分.
(2)女生检测成绩表中的m= ,n= .
(3)已知该校有男生545人,女生360人,若认定检测成绩不低于9分的为“优秀”,请估计全校检测成绩达到“优秀”的人数.
13.某校举行校园安全知识竞赛活动,从七、八年级学生的知识问答成绩中,各随机抽取了20名学生的成绩进行统计分析,绘制了如图所示的统计图和统计表.
样本中学生成绩统计表
七年级 八年级
平均数/分 7.65 7.55
中位数/分 8 b
众数/分 a 7
(1)根据题目信息填空:a= ,b= ,m= .
(2)若七年级的小宇和八年级的小乐的分数都为8分,请判断小宇、小乐在各自年级的排名哪位更靠前.请简述你的理由.
(3)若该校七年级有16个班,每个班有50名学生,请估计七年级学生中成绩优秀(9分及9分以上为优秀)的人数.
14. 水资源问题是全球关注的热点,节约用水已成为全民共识.某校课外兴趣小组想了解居民家庭用水情况,他们从一小区随机抽取了30户家庭,收集了这30户家庭去年7月份的用水量,并对这30个数据进行整理,绘制了如下统计图表:
组别 用水量x/m3 组内平均数/m3
A 2≤x<6 5.3
B 6≤x<10 8.0
C 10≤x<14 12.5
D 14≤x<18 15.5
根据以上信息,解答下列问题:
(1)这30个数据的中位数落在 (填组别)组.
(2)求这30户家庭去年7月份的总用水量.
(3)该小区有1 000户家庭,若每户家庭今年7月份的用水量都比去年7月份各自家庭的用水量节约10%,请估计这1 000户家庭今年7月份的总用水量比去年7月份的总用水量节约多少立方米
15.【2024·河北中考】某公司为提高员工的专业能力,定期对员工进行技能测试.考虑多种因素影响,需将测试的原始成绩x(单位:分)换算为报告成绩y(单位:分).已知原始成绩满分150分,报告成绩满分100分,换算规则如下:
当0≤x当p≤x≤150时,y=+80.
(其中p是小于150的常数,是原始成绩的合格分数线,80是报告成绩的合格分数线)公司规定报告成绩为80分及80分以上(原始成绩为p及p以上)为合格.
(1)甲、乙的原始成绩分别为95分和130分,若p=100,求甲、乙的报告成绩.
(2)丙、丁的报告成绩分别为92分和64分,若丙的原始成绩比丁的原始成绩高40分,请推算p的值.
(3)下表是该公司100名员工某次测试的原始成绩统计表:
原始成 绩/分 95 100 105 110 115 120 125 130 135 140 145 150
人数 1 2 2 5 8 10 7 16 20 15 9 5
①直接写出这100名员工原始成绩的中位数;
②若①中的中位数换算成报告成绩为90分,直接写出该公司此次测试的合格率.
【参考答案】
专题提升
1.A 2.B
3.A 【解析】校对前5个数据为50,60,60,85,90,
则中位数是60,众数是60,平均数是=69(分);
校对后5个数据为50,60,60,85,85,
则中位数是60,众数为60和85,平均数是=68(分);
∴集中趋势不变的只有中位数.
故选A.
4.9 【解析】根据条形统计图可知,得9分的班数最多,为13人,即众数为9分.
故答案为9.
5.乙 【解析】∵=,=2.3,=1.2,
∴<,
∴成绩更稳定的是乙.
故答案为乙.
6.89
7.(1)7.4 (2)> 【解析】(1)(5+10+9+5+8)÷5=7.4(环).
故答案为7.4.
(2)由图表数据可知,甲数据偏离平均数数据较大,乙数据偏离平均数据较小,
即甲波动性较大,即甲方差大.
故答案为>.
8.【解析】(1)这组打分数据的平均数为×(1×2+2×3+3×4+4×5+5×6)=3.5(分).
∵数据的个数是20,
∴中位数是第10,11个数的平均数,
∴这组打分数据的中位数是=4(分).
∵这组打分数据中5分出现的次数最多,
∴这组打分数据的众数是5分.
答:这组打分数据的平均数为3.5分,众数为5分,中位数为4分.
(2)设后来随机抽取了x人,
根据题意得2+3+4+x≥5+6,
∴x≥2,
∴后来最少随机抽取了2名观众.
故答案为2.
9.【解析】(1)a==7.5(分),
b=7(分),
c=×100%=25%.
故答案为7.5;7;25%.
(2)小祺的观点比较片面.
理由不唯一,例如:①甲组成绩的优秀率为37.5%,高于乙组成绩的优秀率25%,
∴从优秀率的角度看,甲组成绩比乙组好.
②甲组成绩的中位数为7.5,高于乙组成绩的中位数,
∴从中位数的角度看,甲组成绩比乙组好.
因此不能仅从平均数的角度说明两组成绩一样好,可见,小祺的观点比较片面.
10.【解析】(1)平均数为
=7.5,
由条形图可知,第20个和21个数据都是8分,
∴中位数为=8,
出现次数最多的是8分,故众数为8.
(2)∵平均数与之前的平均数相同,
∴劳动老师最后抽取的2份问卷中家长所打分数的和为7.5×2=15(分),
∴最后抽取的2份问卷的具体分数为7分和8分或5分和10分或6分和9分.
11.【解析】(1)由折线图可得甲得分更稳定.
把乙的六次成绩按从小到大的顺序排序,第三次、第四次的成绩分别为28和30,
故中位数为==29.
故答案为甲;29.
(2)因为甲的平均每场得分大于乙的平均每场得分,且甲的得分更稳定,所以甲队员表现更好.(注:答案不唯一,合理即可)
(3)甲的综合得分为26.5×1+8×1.5+2×(-1)=36.5,
乙的综合得分为26×1+10×1.5+3×(-1)=38.
因为38>36.5,所以乙队员表现更好.
12.【解析】(1)样本中男生检测成绩为10分的学生数是10×(1-10%-50%-20%)=2(人).
∵出现次数最多的为8分,
∴男生检测成绩的众数为8分.
故答案为2;8.
(2)将女生检测成绩从小到大排列后,它的中位数应是第5个和第6个数据的平均数.
∵女生检测成绩的中位数为8.5分,
∴第5个和第6个数据的和为8.5×2=17=8+9,
∴第5个和第6个数据分别为8分,9分.
∵成绩为6分和7分的人数为1+2=3,
∴成绩为8分的人数为5-3=2,
成绩为10分的人数为5-3=2,
即m=2,n=2.
故答案为2;2.
(3)545×(20%+20%)+360×=218+180=398(人).
答:估计全校检测成绩达到“优秀”的人数为398.
13.【解析】(1)由七年级学生成绩的扇形统计图可知,a=9,m%=100%-30%-10%-15%-10%-20%=15%;
由八年级学生成绩的条形统计图可知,b==7.
故答案为9;7;15.
(2)八年级小乐的排名更靠前.
理由:∵七年级的中位数是8,八年级的中位数是7,
∴分数都为8时,小乐的排名更靠前.
(3)16×50×(30%+15%)=360(人).
答:七年级学生中成绩优秀的约有360人.
14.【解析】(1)根据这30户家庭去年7月份的用水量可得数据,再将其数据从小到大排列,排在中间的两个数落在B组.
故答案为B.
(2)这30户家庭去年7月份的总用水量为5.3×10+8.0×12+12.5×6+15.5×2=255(m3).
(3)这30户家庭去年7月份的平均用水量为255÷30=8.5(m3).
∵这1 000户家庭去年7月份的总用水量为8.5×1 000=8 500(m3),
∴该1 000户家庭今年7月份的总用水量比去年节约了8 500×10%=850(m3).
答:这1 000户家庭今年7月份的总用水量比去年7月份的总用水量节约850 m3.
15.【解析】(1)当p=100时,甲的报告成绩为y==76(分),
乙的报告成绩为y=+80=92(分).
(2)∵92>80,
∴当y=92时,+80=92,
解得x丙=90+p.
∵64<80,
∴当y=64时,=64,
解得x丁=p.
∵x丙-x丁=40,
∴90+p-p=40,
解得p=125.
(3)①共计100名员工,且成绩已经排列好,
∴中位数是第50,51名员工成绩的平均数,
由表格得第50,51名员工成绩都是130分,
∴中位数为130.
②90=+80,
解得p=110,符合题意,
∴由表格得到原始成绩为110及110以上的人数为100-(1+2+2)=95,
∴合格率为×100%=95%.
◆必记公式 1.算式平均数公式:=(x1+x2+…+xn). 2.加权平均数公式:=(其中f1+f2+…+fk=n). 3.方差公式:s2=[(x1-)2+(x2-)2+…+(xn-)2].
【专题提升】
1.一组数据-2,5,3,7,增加一个数据后,众数为7,则增加数据后中位数是 ()
A.5 B.3 C.4 D.7
2.在电脑上,为了让使用者直观地看出磁盘“已用空间”与“可用空间”占“整个磁盘空间”的百分比,使用的统计图应该是 ()
A.条形统计图 B.扇形统计图
C.折线统计图 D.以上都可以
3.一次测试中,五名同学的得分分别为60,85,50,60,90,后经过校对发现,得90分的同学应得85分,校对后的五个数据与之前五个数据相比,集中趋势不变的是 ()
A.只有中位数 B.只有平均数
C.只有众数 D.中位数与众数
4.【2024·河南中考】2024年3月是第8个全国近视防控宣传教育月,其主题是“有效减少近视发生,共同守护光明未来”.某校组织各班围绕这个主题开展板报宣传活动,并对各班的宣传板报进行评分,得分情况如图,则得分的众数为 分.
5.如图,投壶是中国古代一种传统礼仪和宴饮游戏.在一次投壶比赛中,甲、乙两人成绩的平均数分别为,,方差分别为,.若=,=2.3,=1.2,则成绩更稳定的是 (填“甲”或“乙”).
6.【2024·河北中考】某校生物小组的9名同学各用100粒种子做发芽实验,几天后观察并记录种子的发芽数分别为89,73,90,86,75,86,89,95,89,以上数据中的众数为 .
7.甲、乙两人进行了五次射击测试,测试成绩如图所示:
(1)甲测试成绩的平均数是 环.
(2)甲、乙两人成绩的方差记为,,则 (填“>”“<”或“=”).
8.为了解某电影在五一假期的上映满意度,随机抽取了部分观众对这部电影进行打分(打分按从高到低分为5个分值:5分、4分、3分、2分、1分),根据调查结果,绘制出如图所示的统计图.
(1)分别求这组打分数据的平均数、众数和中位数.
(2)后来又另外随机抽取几名观众对这部电影进行打分,得知这几名观众的打分均小于4分,将这次打分的数据与之前的数据合并后发现中位数发生了改变,则后来最少随机抽取了 名观众.
9. 为激发青少年崇尚科学、探索未知的热情,学校开展“科学小博士”知识竞赛.各班以小组为单位组织初赛,规定满分为10分、9分及以上为优秀.
数据整理:小夏将本班甲、乙两组同学(每组8人)初赛的成绩整理成如下的统计图.
数据分析:小夏对这两个小组的成绩进行了如下分析.
平均数/分 中位数/分 众数/分 方差 优秀率
甲组 7.625 a 7 4.48 37.5%
乙组 7.625 7 b 0.73 c
请认真阅读上述信息,回答下列问题:
(1)填空:a= ,b= ,c= .
(2)小祺认为甲、乙两组成绩的平均数相等,因此两个组成绩一样好.小夏认为小祺的观点比较片面,请结合上表中的信息帮小夏说明理由(写出两条即可).
10.某校为了解学生校外的劳动表现,对全校学生进行了问卷调查,让每位学生的家长对自家孩子打分,分数为5分、6分、7分、8分、9分、10分,共6档.劳动老师从全部的问卷中随机抽取了40份,下图是根据这40份问卷中的家长所打分数绘制的统计图.
(1)求被抽取的家长们所打分数的平均数、中位数和众数.
(2)劳动老师从余下的问卷中又随机抽取了2份,与之前的40份合在一起,重新计算后,发现家长所打分数的平均数与之前的平均数相同,求劳动老师最后抽取的2份问卷中家长所打分数的和,并直接写出一种最后抽取的2份问卷的具体分数.
11.【2024·河南中考】为提升学生体质健康水平,促进学生全面发展,学校开展了丰富多彩的课外体育活动.在八年级组织的篮球联赛中,甲、乙两名队员表现优异,他们在近六场比赛中关于得分、篮板和失误三个方面的统计结果如下.
技术统计表
队员 平均每场得分 平均每场篮板 平均每场失误
甲 26.5 8 2
乙 26 10 3
根据以上信息,回答下列问题:
(1)这六场比赛中,得分更稳定的队员是 (填“甲”或“乙”);甲队员得分的中位数为27.5分,乙队员得分的中位数为 分.
(2)请从得分方面分析:这六场比赛中,甲、乙两名队员谁的表现更好.
(3)规定“综合得分”为平均每场得分×1+平均每场篮板×1.5+平均每场失误×(-1),且综合得分越高表现越好.请利用这种评价方法,比较这六场比赛中甲、乙两名队员谁的表现更好.
小情境主题:安全第一
12.环球网消息称:近年来的电动自行车火灾事故80%都是在充电时发生的,超过一半的电动自行车火灾发生在夜间充电的过程中.为了规避风险,某校政教处对学生进行规范充电培训活动,并对培训效果按10分制进行检测评分.为了解这次培训的效果,现从各年级随机抽取男、女生各10名的检测成绩作为样本进行整理,并绘制成如下不完整的统计图表:
抽取的10名女生检测成绩统计表
成绩/分 6 7 8 9 10
人数 1 2 m 3 n
注:10名女生检测成绩的中位数为8.5分.
抽取的10名男生检测成绩扇形图
请根据以上信息,回答下列问题:
(1)样本中男生检测成绩为10分的学生数是 ,众数为 分.
(2)女生检测成绩表中的m= ,n= .
(3)已知该校有男生545人,女生360人,若认定检测成绩不低于9分的为“优秀”,请估计全校检测成绩达到“优秀”的人数.
13.某校举行校园安全知识竞赛活动,从七、八年级学生的知识问答成绩中,各随机抽取了20名学生的成绩进行统计分析,绘制了如图所示的统计图和统计表.
样本中学生成绩统计表
七年级 八年级
平均数/分 7.65 7.55
中位数/分 8 b
众数/分 a 7
(1)根据题目信息填空:a= ,b= ,m= .
(2)若七年级的小宇和八年级的小乐的分数都为8分,请判断小宇、小乐在各自年级的排名哪位更靠前.请简述你的理由.
(3)若该校七年级有16个班,每个班有50名学生,请估计七年级学生中成绩优秀(9分及9分以上为优秀)的人数.
14. 水资源问题是全球关注的热点,节约用水已成为全民共识.某校课外兴趣小组想了解居民家庭用水情况,他们从一小区随机抽取了30户家庭,收集了这30户家庭去年7月份的用水量,并对这30个数据进行整理,绘制了如下统计图表:
组别 用水量x/m3 组内平均数/m3
A 2≤x<6 5.3
B 6≤x<10 8.0
C 10≤x<14 12.5
D 14≤x<18 15.5
根据以上信息,解答下列问题:
(1)这30个数据的中位数落在 (填组别)组.
(2)求这30户家庭去年7月份的总用水量.
(3)该小区有1 000户家庭,若每户家庭今年7月份的用水量都比去年7月份各自家庭的用水量节约10%,请估计这1 000户家庭今年7月份的总用水量比去年7月份的总用水量节约多少立方米
15.【2024·河北中考】某公司为提高员工的专业能力,定期对员工进行技能测试.考虑多种因素影响,需将测试的原始成绩x(单位:分)换算为报告成绩y(单位:分).已知原始成绩满分150分,报告成绩满分100分,换算规则如下:
当0≤x
(其中p是小于150的常数,是原始成绩的合格分数线,80是报告成绩的合格分数线)公司规定报告成绩为80分及80分以上(原始成绩为p及p以上)为合格.
(1)甲、乙的原始成绩分别为95分和130分,若p=100,求甲、乙的报告成绩.
(2)丙、丁的报告成绩分别为92分和64分,若丙的原始成绩比丁的原始成绩高40分,请推算p的值.
(3)下表是该公司100名员工某次测试的原始成绩统计表:
原始成 绩/分 95 100 105 110 115 120 125 130 135 140 145 150
人数 1 2 2 5 8 10 7 16 20 15 9 5
①直接写出这100名员工原始成绩的中位数;
②若①中的中位数换算成报告成绩为90分,直接写出该公司此次测试的合格率.
【参考答案】
专题提升
1.A 2.B
3.A 【解析】校对前5个数据为50,60,60,85,90,
则中位数是60,众数是60,平均数是=69(分);
校对后5个数据为50,60,60,85,85,
则中位数是60,众数为60和85,平均数是=68(分);
∴集中趋势不变的只有中位数.
故选A.
4.9 【解析】根据条形统计图可知,得9分的班数最多,为13人,即众数为9分.
故答案为9.
5.乙 【解析】∵=,=2.3,=1.2,
∴<,
∴成绩更稳定的是乙.
故答案为乙.
6.89
7.(1)7.4 (2)> 【解析】(1)(5+10+9+5+8)÷5=7.4(环).
故答案为7.4.
(2)由图表数据可知,甲数据偏离平均数数据较大,乙数据偏离平均数据较小,
即甲波动性较大,即甲方差大.
故答案为>.
8.【解析】(1)这组打分数据的平均数为×(1×2+2×3+3×4+4×5+5×6)=3.5(分).
∵数据的个数是20,
∴中位数是第10,11个数的平均数,
∴这组打分数据的中位数是=4(分).
∵这组打分数据中5分出现的次数最多,
∴这组打分数据的众数是5分.
答:这组打分数据的平均数为3.5分,众数为5分,中位数为4分.
(2)设后来随机抽取了x人,
根据题意得2+3+4+x≥5+6,
∴x≥2,
∴后来最少随机抽取了2名观众.
故答案为2.
9.【解析】(1)a==7.5(分),
b=7(分),
c=×100%=25%.
故答案为7.5;7;25%.
(2)小祺的观点比较片面.
理由不唯一,例如:①甲组成绩的优秀率为37.5%,高于乙组成绩的优秀率25%,
∴从优秀率的角度看,甲组成绩比乙组好.
②甲组成绩的中位数为7.5,高于乙组成绩的中位数,
∴从中位数的角度看,甲组成绩比乙组好.
因此不能仅从平均数的角度说明两组成绩一样好,可见,小祺的观点比较片面.
10.【解析】(1)平均数为
=7.5,
由条形图可知,第20个和21个数据都是8分,
∴中位数为=8,
出现次数最多的是8分,故众数为8.
(2)∵平均数与之前的平均数相同,
∴劳动老师最后抽取的2份问卷中家长所打分数的和为7.5×2=15(分),
∴最后抽取的2份问卷的具体分数为7分和8分或5分和10分或6分和9分.
11.【解析】(1)由折线图可得甲得分更稳定.
把乙的六次成绩按从小到大的顺序排序,第三次、第四次的成绩分别为28和30,
故中位数为==29.
故答案为甲;29.
(2)因为甲的平均每场得分大于乙的平均每场得分,且甲的得分更稳定,所以甲队员表现更好.(注:答案不唯一,合理即可)
(3)甲的综合得分为26.5×1+8×1.5+2×(-1)=36.5,
乙的综合得分为26×1+10×1.5+3×(-1)=38.
因为38>36.5,所以乙队员表现更好.
12.【解析】(1)样本中男生检测成绩为10分的学生数是10×(1-10%-50%-20%)=2(人).
∵出现次数最多的为8分,
∴男生检测成绩的众数为8分.
故答案为2;8.
(2)将女生检测成绩从小到大排列后,它的中位数应是第5个和第6个数据的平均数.
∵女生检测成绩的中位数为8.5分,
∴第5个和第6个数据的和为8.5×2=17=8+9,
∴第5个和第6个数据分别为8分,9分.
∵成绩为6分和7分的人数为1+2=3,
∴成绩为8分的人数为5-3=2,
成绩为10分的人数为5-3=2,
即m=2,n=2.
故答案为2;2.
(3)545×(20%+20%)+360×=218+180=398(人).
答:估计全校检测成绩达到“优秀”的人数为398.
13.【解析】(1)由七年级学生成绩的扇形统计图可知,a=9,m%=100%-30%-10%-15%-10%-20%=15%;
由八年级学生成绩的条形统计图可知,b==7.
故答案为9;7;15.
(2)八年级小乐的排名更靠前.
理由:∵七年级的中位数是8,八年级的中位数是7,
∴分数都为8时,小乐的排名更靠前.
(3)16×50×(30%+15%)=360(人).
答:七年级学生中成绩优秀的约有360人.
14.【解析】(1)根据这30户家庭去年7月份的用水量可得数据,再将其数据从小到大排列,排在中间的两个数落在B组.
故答案为B.
(2)这30户家庭去年7月份的总用水量为5.3×10+8.0×12+12.5×6+15.5×2=255(m3).
(3)这30户家庭去年7月份的平均用水量为255÷30=8.5(m3).
∵这1 000户家庭去年7月份的总用水量为8.5×1 000=8 500(m3),
∴该1 000户家庭今年7月份的总用水量比去年节约了8 500×10%=850(m3).
答:这1 000户家庭今年7月份的总用水量比去年7月份的总用水量节约850 m3.
15.【解析】(1)当p=100时,甲的报告成绩为y==76(分),
乙的报告成绩为y=+80=92(分).
(2)∵92>80,
∴当y=92时,+80=92,
解得x丙=90+p.
∵64<80,
∴当y=64时,=64,
解得x丁=p.
∵x丙-x丁=40,
∴90+p-p=40,
解得p=125.
(3)①共计100名员工,且成绩已经排列好,
∴中位数是第50,51名员工成绩的平均数,
由表格得第50,51名员工成绩都是130分,
∴中位数为130.
②90=+80,
解得p=110,符合题意,
∴由表格得到原始成绩为110及110以上的人数为100-(1+2+2)=95,
∴合格率为×100%=95%.
