第十八章 平行四边形 章末小结与提升(含详解) 2024-2025学年人教版初中数学八年级下册
文档属性
| 名称 | 第十八章 平行四边形 章末小结与提升(含详解) 2024-2025学年人教版初中数学八年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 606.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-03 00:00:00 | ||
图片预览




文档简介
第十八章 平行四边形 章末小结与提升
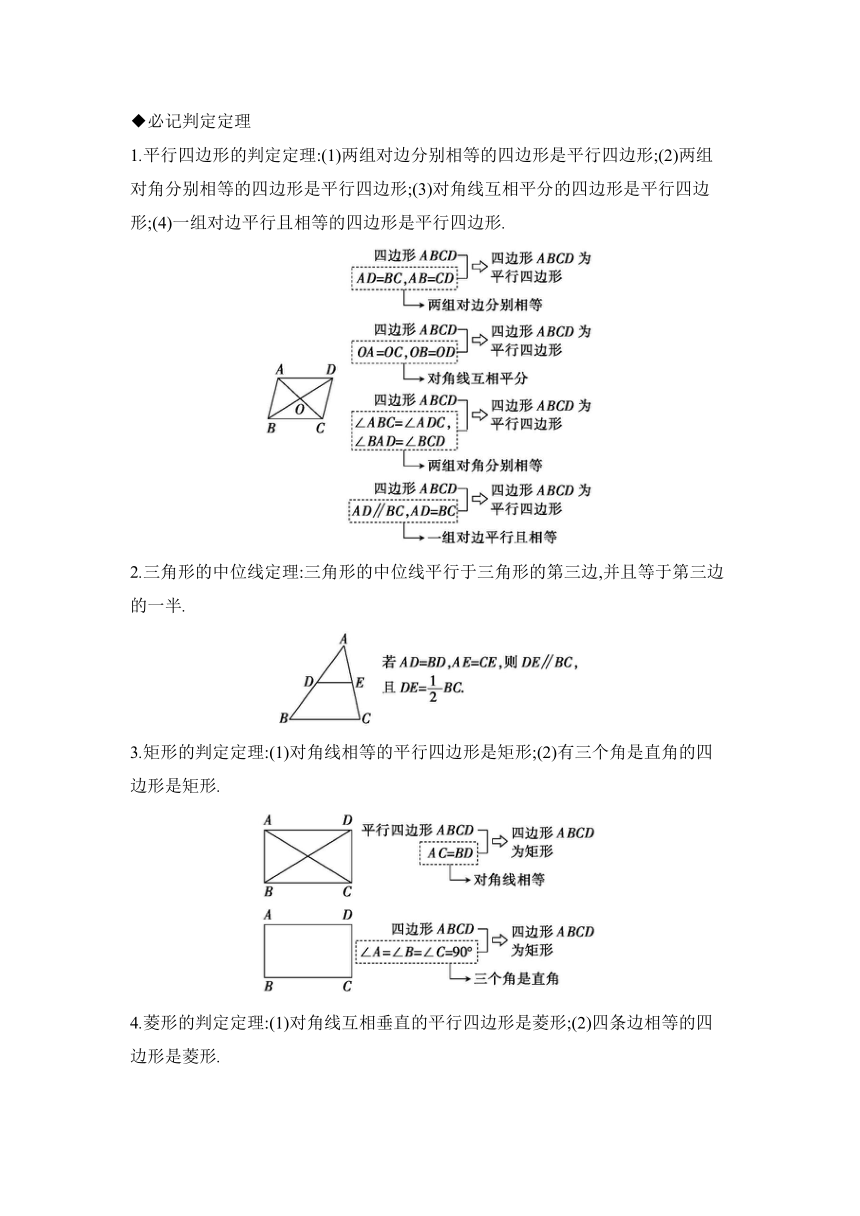
◆必记性质定理 1.平行四边形的性质:(1)平行四边形的对边相等;(2)平行四边形的对角相等;(3)平行四边形的对角线互相平分. 2.矩形的性质:(1)矩形的四个角都是直角;(2)矩形的对角线相等. 3.直角三角形斜边中线的性质:直角三角形斜边上的中线等于斜边的一半. 4.菱形的性质:(1)菱形的四条边都相等;(2)菱形的两条对角线互相垂直,并且每一条对角线平分一组对角. 5.正方形的性质:(1)正方形的四条边都相等;(2)正方形的四个角都是直角;(3)正方形的对角线互相垂直平分且相等,每一条对角线平分一组对角.
◆必记判定定理 1.平行四边形的判定定理:(1)两组对边分别相等的四边形是平行四边形;(2)两组对角分别相等的四边形是平行四边形;(3)对角线互相平分的四边形是平行四边形;(4)一组对边平行且相等的四边形是平行四边形. 2.三角形的中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半. 3.矩形的判定定理:(1)对角线相等的平行四边形是矩形;(2)有三个角是直角的四边形是矩形. 4.菱形的判定定理:(1)对角线互相垂直的平行四边形是菱形;(2)四条边相等的四边形是菱形.
5.正方形的判定定理:(1)有一组邻边相等的矩形是正方形;(2)有一个角是直角的菱形是正方形.
【专题提升】
1.生活中处处皆数学,如图所示的是“左侧通行”交通标识,其中四边形ABCD为平行四边形.若∠BAD=140°,则∠BCD的度数为 ()
A.40° B.100°
C.120° D.140°
2.下图是不完整的推理过程,为保证推理成立,需在四边形ABCD中添加条件.对于嘉嘉和淇淇添加的条件,下列判断正确的是 ()
嘉嘉:AD∥BC.淇淇:AB=CD.
A.只有嘉嘉正确
B.只有淇淇正确
C.两人都正确
D.两人都不正确
3. 如图,构成伸缩门的基本图形是菱形,且每个小菱形的边长都为0.4米,伸缩门伸展到最宽时为8米,此时菱形的一个内角为60°.若中间隔板的厚度不计,则图中的n为 ()
A.10 B.15
C.20 D.25
4.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠BCD=18°,E是斜边AB的中点,则∠DCE的度数为 ()
A.30° B.36°
C.45° D.54°
5.在 ABCD中,EF经过两条对角线的交点O,分别交AB,CD于点E,F,在对角线AC上通过作图得到点M,N,如图1、图2、图3.下面关于以F,M,E,N为顶点的四边形的形状的说法正确的是 ()
以点O为圆心,OE的长为半径作弧,交AC于点M,N 分别作△AOE、△COF中OA,OC边上的中线EM,FN 分别作△AOE、△COF中∠AEO,∠CFO的平分线EM,FN
A.都为矩形
B.都为菱形
C.图1为平行四边形,图2、图3为矩形
D.图1为矩形,图2、图3为平行四边形
小情境主题:五育并举
6.为了更好地开展劳动教育,实现五育并举,某校开设了劳动实践课程,在—个三角形地块中分出一块(阴影部分)作为劳动实践用地,尺寸如图所示,则PQ的长是 ()
A.2 m B.3 m C.4 m D.5 m
7.如图,某公园有一块三角形空地ABC,BC=12米,沿DE放置一道栅栏把△ABC分成两个区域种植不同的花卉,D,E分别是AB,AC的中点,则栅栏DE的长为 米.
8.如图,在矩形ABCD中,AD=5,AB=3,E为BC上的一点,EA平分∠BED,则BE的长为 .
9.现有一个零件,如图1.嘉嘉和琪琪分析零件所标数据后,嘉嘉认为此零件是矩形,琪琪认为此零件不是矩形,你同意谁的说法,借助图2进行说明.
10.如图,在平行四边形ABCD中,DE⊥BC于点E.
(1)尺规作图:过点A作AF⊥CD交CD的延长线于点F.(保留作图痕迹,不写作法)
(2)若DE=AF,求证:平行四边形ABCD为菱形.
11.如图,在平行四边形ABCD中,E,F分别为BC,AD的中点,DE平分∠ADC.
(1)求证:四边形ECDF是平行四边形.
(2)求证:AD=2AB.
(3)若CE=5,DE=8,求点A到边BC的距离.
12.【问题情境】
如图1,在矩形ABCD中,AB=4,AD=6.将边AB绕点A逆时针旋转α(0°<α<180°)得到线段AE,过点E作EF⊥AE交BC于点F.
【猜想证明】
(1)当α=90°时,判断四边形ABFE的形状并说明理由.
(2)如图2,当α=45°时,连接DE,求此时△ADE的面积.
【能力提升】
(3)在【问题情境】的条件下,是否存在α,使点F,E,D三点共线.若存在,请直接写出此时BF的长;若不存在,请说明理由.
【参考答案】
专题提升
1.D 【解析】∵四边形ABCD为平行四边形,
∴∠BCD=∠BAD=140°.
故选D.
2.C 【解析】根据两组对边分别平行的四边形是平行四边形,可以添加AD∥BC;
根据一组对边平行且相等的四边形是平行四边形,可以添加AB=CD;
∴两人都正确.
故选C.
3.C 【解析】∵每个小菱形的边长都为0.4米,菱形的一个内角为60°,∴较短的对角线的长为0.4米.∵总长度为8米,∴图中的n为8÷0.4=20.故选C.
4.D 【解析】∵∠ACB=∠ACD+∠BCD=90°,∠BCD=18°,
∴∠ACD=72°.∵CD⊥AB,∴在Rt△BCD中,∠B=90°-∠BCD=90°-18°=72°.同理,在Rt△ABC中,∠A=90°-∠B=90°-72°=18°.∵E是AB的中点,即CE=BE=AE,∴∠ECA=∠A=18°,
∴∠DCE=∠ACD-∠ACE=72°-18°=54°.
故选D.
5.D 【解析】在平行四边形ABCD中,AB∥DC,OA=OC,
∴∠FCO=∠EAO,∠CFO=∠AEO,
在△FCO和△EAO中,
∴△FCO≌△EAO(AAS),
∴OE=OF,
由图1作图可得OE=OF=OM=ON,
∴图1中以F,M,E,N为顶点的四边形为矩形.
由图2作图可得OM=AM=OA,ON=NC=OC.
∵OA=OC,
∴OM=ON.
又∵OE=OF,
∴图2中以F,M,E,N为顶点的四边形为平行四边形.
由图3作图可得∠AEM=∠OEM=∠AEF,∠CFN=∠NFO=∠CFE.
∵∠CFO=∠AEO,
∴∠OEM=∠NFO,
在△FON和△EOM中,
∴△FON≌△EOM(ASA),
∴OM=ON.
又∵OE=OF,
∴图3中以F,M,E,N为顶点的四边形为平行四边形.
故选D.
6.D 【解析】如图,
∵PA=PB=8 m,QC=QA=10 m,
∴P,Q分别是AB,AC的中点,
∴PQ是△ABC的中位线,
∴BC=2PQ.
∵BC=10 m,
∴PQ=5 m.
故选D.
7.6 【解析】∵D,E分别是AB,AC的中点,
∴DE是△ABC的中位线,
∴DE=BC=6(米).
故答案为6.
8.1 【解析】∵EA平分∠BED,
∴∠AEB=∠AED.
∵四边形ABCD是矩形,AD=5,AB=3,
∴AB=CD=3,AD=BC=5,AD∥BC,∠C=90°,
∴∠DAE=∠AEB,
∴∠DAE=∠AED,
∴AD=ED=5,
∴EC===4,
∴BE=BC-EC=5-4=1.
故答案为1.
9.【解析】同意嘉嘉的说法.
理由:由图可知OA=OB=OC=OD,
∴四边形ABCD是平行四边形.
又∵AC=BD,
∴四边形ABCD是矩形.
10.【解析】(1)如图,AF为所作.
(2)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADF=∠C.
∵DE⊥BC,AF⊥CD,
∴∠DEC=∠AFD=90°.
在△AFD与△DEC中,
∴△AFD≌△DEC(AAS),
∴AD=DC,
∴平行四边形ABCD是菱形(邻边相等的平行四边形为菱形).
11.【解析】(1)证明:在平行四边形ABCD中,AD∥BC,AD=BC.
∵E,F分别为BC,AD的中点,
∴DF=AD=BC=EC,
∴四边形ECDF为平行四边形.
(2)证明:∵DE平分∠ADC,
∴∠FDE=∠EDC.
∵四边形ABCD为平行四边形,
∴AD∥BC,AB=CD,AD=BC,
∴∠FDE=∠DEC,
∴∠EDC=∠DEC,
∴EC=CD,
∴EC=AB.
∵E是BC的中点,
∴BC=2EC,
∴AD=BC=2AB.
(3)如图,连接FC,交DE于点O.
∵四边形ECDF为平行四边形,EC=CD,
∴四边形ECDF为菱形,
∴DE⊥CF,且DE,CF互相平分.
∵DE=8,
∴DO=EO=4.
∵CE=5,
∴CO===3,
∴CF=2CO=6,
∴S△ECF=CF·EO=×6×4=12.
∵AD∥BC,
∴点F到BC的距离即点A到BC的距离,
设点F到BC的距离为h,
根据△ECF的面积,可得×5h=12,
∴h=,
∴点F到边BC的距离为,即点A到边BC的距离为.
12.【解析】(1)如图1.当α=90°时,四边形ABFE是正方形.理由如下:
∵四边形ABCD是矩形,
∴∠A=∠B=90°.
∵将边AB绕点A逆时针旋转α(0°<α<180°)得到线段AE,
∴AE=AB,∠EAB=90°,∠AEF=90°,
∴∠B=∠EAB=∠AEF=90°,
∴四边形ABFE是矩形.
∵AE=AB,
∴四边形ABFE是正方形.
(2)如图2,作EG⊥AD于点G.
∵∠BAD=90°,∠BAE=45°,
∴∠EAG=45°,
∴∠AEG=90°-∠EAG=45°,
∴∠AEG=∠EAG,
∴AG=EG.
∵EG2+AG2=AE2,
∴2EG2=42,
∴EG=2,
∴S△ADE=AD·EG=×6×2=6.
(3)如图3,当点E在DF上时,连接AF.
∵∠AEF=∠B=90°,AE=AB,AF=AF,
∴Rt△ABF≌Rt△AEF(HL),
∴BF=EF,
设BF=EF=x,则CF=6-x,
根据旋转的性质得AE=AB=4.
∵EF⊥AE,
∴∠AED=∠AEF=90°.
∵AD=6,
∴DE===2,
在Rt△DCF中,由勾股定理得CF2+CD2=DF2,
(6-x)2+42=(x+2)2,
解得x=6-2.
如图4,当点E在FD的延长线上时,
同理EF=BF,DE=2,
设EF=BF=b,则DF=b-2,CF=b-6,
∴(b-6)2+42=(b-2)2,
解得b=6+2.
综上所述,BF的长为6-2或6+2.
◆必记性质定理 1.平行四边形的性质:(1)平行四边形的对边相等;(2)平行四边形的对角相等;(3)平行四边形的对角线互相平分. 2.矩形的性质:(1)矩形的四个角都是直角;(2)矩形的对角线相等. 3.直角三角形斜边中线的性质:直角三角形斜边上的中线等于斜边的一半. 4.菱形的性质:(1)菱形的四条边都相等;(2)菱形的两条对角线互相垂直,并且每一条对角线平分一组对角. 5.正方形的性质:(1)正方形的四条边都相等;(2)正方形的四个角都是直角;(3)正方形的对角线互相垂直平分且相等,每一条对角线平分一组对角.
◆必记判定定理 1.平行四边形的判定定理:(1)两组对边分别相等的四边形是平行四边形;(2)两组对角分别相等的四边形是平行四边形;(3)对角线互相平分的四边形是平行四边形;(4)一组对边平行且相等的四边形是平行四边形. 2.三角形的中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半. 3.矩形的判定定理:(1)对角线相等的平行四边形是矩形;(2)有三个角是直角的四边形是矩形. 4.菱形的判定定理:(1)对角线互相垂直的平行四边形是菱形;(2)四条边相等的四边形是菱形.
5.正方形的判定定理:(1)有一组邻边相等的矩形是正方形;(2)有一个角是直角的菱形是正方形.
【专题提升】
1.生活中处处皆数学,如图所示的是“左侧通行”交通标识,其中四边形ABCD为平行四边形.若∠BAD=140°,则∠BCD的度数为 ()
A.40° B.100°
C.120° D.140°
2.下图是不完整的推理过程,为保证推理成立,需在四边形ABCD中添加条件.对于嘉嘉和淇淇添加的条件,下列判断正确的是 ()
嘉嘉:AD∥BC.淇淇:AB=CD.
A.只有嘉嘉正确
B.只有淇淇正确
C.两人都正确
D.两人都不正确
3. 如图,构成伸缩门的基本图形是菱形,且每个小菱形的边长都为0.4米,伸缩门伸展到最宽时为8米,此时菱形的一个内角为60°.若中间隔板的厚度不计,则图中的n为 ()
A.10 B.15
C.20 D.25
4.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠BCD=18°,E是斜边AB的中点,则∠DCE的度数为 ()
A.30° B.36°
C.45° D.54°
5.在 ABCD中,EF经过两条对角线的交点O,分别交AB,CD于点E,F,在对角线AC上通过作图得到点M,N,如图1、图2、图3.下面关于以F,M,E,N为顶点的四边形的形状的说法正确的是 ()
以点O为圆心,OE的长为半径作弧,交AC于点M,N 分别作△AOE、△COF中OA,OC边上的中线EM,FN 分别作△AOE、△COF中∠AEO,∠CFO的平分线EM,FN
A.都为矩形
B.都为菱形
C.图1为平行四边形,图2、图3为矩形
D.图1为矩形,图2、图3为平行四边形
小情境主题:五育并举
6.为了更好地开展劳动教育,实现五育并举,某校开设了劳动实践课程,在—个三角形地块中分出一块(阴影部分)作为劳动实践用地,尺寸如图所示,则PQ的长是 ()
A.2 m B.3 m C.4 m D.5 m
7.如图,某公园有一块三角形空地ABC,BC=12米,沿DE放置一道栅栏把△ABC分成两个区域种植不同的花卉,D,E分别是AB,AC的中点,则栅栏DE的长为 米.
8.如图,在矩形ABCD中,AD=5,AB=3,E为BC上的一点,EA平分∠BED,则BE的长为 .
9.现有一个零件,如图1.嘉嘉和琪琪分析零件所标数据后,嘉嘉认为此零件是矩形,琪琪认为此零件不是矩形,你同意谁的说法,借助图2进行说明.
10.如图,在平行四边形ABCD中,DE⊥BC于点E.
(1)尺规作图:过点A作AF⊥CD交CD的延长线于点F.(保留作图痕迹,不写作法)
(2)若DE=AF,求证:平行四边形ABCD为菱形.
11.如图,在平行四边形ABCD中,E,F分别为BC,AD的中点,DE平分∠ADC.
(1)求证:四边形ECDF是平行四边形.
(2)求证:AD=2AB.
(3)若CE=5,DE=8,求点A到边BC的距离.
12.【问题情境】
如图1,在矩形ABCD中,AB=4,AD=6.将边AB绕点A逆时针旋转α(0°<α<180°)得到线段AE,过点E作EF⊥AE交BC于点F.
【猜想证明】
(1)当α=90°时,判断四边形ABFE的形状并说明理由.
(2)如图2,当α=45°时,连接DE,求此时△ADE的面积.
【能力提升】
(3)在【问题情境】的条件下,是否存在α,使点F,E,D三点共线.若存在,请直接写出此时BF的长;若不存在,请说明理由.
【参考答案】
专题提升
1.D 【解析】∵四边形ABCD为平行四边形,
∴∠BCD=∠BAD=140°.
故选D.
2.C 【解析】根据两组对边分别平行的四边形是平行四边形,可以添加AD∥BC;
根据一组对边平行且相等的四边形是平行四边形,可以添加AB=CD;
∴两人都正确.
故选C.
3.C 【解析】∵每个小菱形的边长都为0.4米,菱形的一个内角为60°,∴较短的对角线的长为0.4米.∵总长度为8米,∴图中的n为8÷0.4=20.故选C.
4.D 【解析】∵∠ACB=∠ACD+∠BCD=90°,∠BCD=18°,
∴∠ACD=72°.∵CD⊥AB,∴在Rt△BCD中,∠B=90°-∠BCD=90°-18°=72°.同理,在Rt△ABC中,∠A=90°-∠B=90°-72°=18°.∵E是AB的中点,即CE=BE=AE,∴∠ECA=∠A=18°,
∴∠DCE=∠ACD-∠ACE=72°-18°=54°.
故选D.
5.D 【解析】在平行四边形ABCD中,AB∥DC,OA=OC,
∴∠FCO=∠EAO,∠CFO=∠AEO,
在△FCO和△EAO中,
∴△FCO≌△EAO(AAS),
∴OE=OF,
由图1作图可得OE=OF=OM=ON,
∴图1中以F,M,E,N为顶点的四边形为矩形.
由图2作图可得OM=AM=OA,ON=NC=OC.
∵OA=OC,
∴OM=ON.
又∵OE=OF,
∴图2中以F,M,E,N为顶点的四边形为平行四边形.
由图3作图可得∠AEM=∠OEM=∠AEF,∠CFN=∠NFO=∠CFE.
∵∠CFO=∠AEO,
∴∠OEM=∠NFO,
在△FON和△EOM中,
∴△FON≌△EOM(ASA),
∴OM=ON.
又∵OE=OF,
∴图3中以F,M,E,N为顶点的四边形为平行四边形.
故选D.
6.D 【解析】如图,
∵PA=PB=8 m,QC=QA=10 m,
∴P,Q分别是AB,AC的中点,
∴PQ是△ABC的中位线,
∴BC=2PQ.
∵BC=10 m,
∴PQ=5 m.
故选D.
7.6 【解析】∵D,E分别是AB,AC的中点,
∴DE是△ABC的中位线,
∴DE=BC=6(米).
故答案为6.
8.1 【解析】∵EA平分∠BED,
∴∠AEB=∠AED.
∵四边形ABCD是矩形,AD=5,AB=3,
∴AB=CD=3,AD=BC=5,AD∥BC,∠C=90°,
∴∠DAE=∠AEB,
∴∠DAE=∠AED,
∴AD=ED=5,
∴EC===4,
∴BE=BC-EC=5-4=1.
故答案为1.
9.【解析】同意嘉嘉的说法.
理由:由图可知OA=OB=OC=OD,
∴四边形ABCD是平行四边形.
又∵AC=BD,
∴四边形ABCD是矩形.
10.【解析】(1)如图,AF为所作.
(2)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADF=∠C.
∵DE⊥BC,AF⊥CD,
∴∠DEC=∠AFD=90°.
在△AFD与△DEC中,
∴△AFD≌△DEC(AAS),
∴AD=DC,
∴平行四边形ABCD是菱形(邻边相等的平行四边形为菱形).
11.【解析】(1)证明:在平行四边形ABCD中,AD∥BC,AD=BC.
∵E,F分别为BC,AD的中点,
∴DF=AD=BC=EC,
∴四边形ECDF为平行四边形.
(2)证明:∵DE平分∠ADC,
∴∠FDE=∠EDC.
∵四边形ABCD为平行四边形,
∴AD∥BC,AB=CD,AD=BC,
∴∠FDE=∠DEC,
∴∠EDC=∠DEC,
∴EC=CD,
∴EC=AB.
∵E是BC的中点,
∴BC=2EC,
∴AD=BC=2AB.
(3)如图,连接FC,交DE于点O.
∵四边形ECDF为平行四边形,EC=CD,
∴四边形ECDF为菱形,
∴DE⊥CF,且DE,CF互相平分.
∵DE=8,
∴DO=EO=4.
∵CE=5,
∴CO===3,
∴CF=2CO=6,
∴S△ECF=CF·EO=×6×4=12.
∵AD∥BC,
∴点F到BC的距离即点A到BC的距离,
设点F到BC的距离为h,
根据△ECF的面积,可得×5h=12,
∴h=,
∴点F到边BC的距离为,即点A到边BC的距离为.
12.【解析】(1)如图1.当α=90°时,四边形ABFE是正方形.理由如下:
∵四边形ABCD是矩形,
∴∠A=∠B=90°.
∵将边AB绕点A逆时针旋转α(0°<α<180°)得到线段AE,
∴AE=AB,∠EAB=90°,∠AEF=90°,
∴∠B=∠EAB=∠AEF=90°,
∴四边形ABFE是矩形.
∵AE=AB,
∴四边形ABFE是正方形.
(2)如图2,作EG⊥AD于点G.
∵∠BAD=90°,∠BAE=45°,
∴∠EAG=45°,
∴∠AEG=90°-∠EAG=45°,
∴∠AEG=∠EAG,
∴AG=EG.
∵EG2+AG2=AE2,
∴2EG2=42,
∴EG=2,
∴S△ADE=AD·EG=×6×2=6.
(3)如图3,当点E在DF上时,连接AF.
∵∠AEF=∠B=90°,AE=AB,AF=AF,
∴Rt△ABF≌Rt△AEF(HL),
∴BF=EF,
设BF=EF=x,则CF=6-x,
根据旋转的性质得AE=AB=4.
∵EF⊥AE,
∴∠AED=∠AEF=90°.
∵AD=6,
∴DE===2,
在Rt△DCF中,由勾股定理得CF2+CD2=DF2,
(6-x)2+42=(x+2)2,
解得x=6-2.
如图4,当点E在FD的延长线上时,
同理EF=BF,DE=2,
设EF=BF=b,则DF=b-2,CF=b-6,
∴(b-6)2+42=(b-2)2,
解得b=6+2.
综上所述,BF的长为6-2或6+2.
