3.4 简单的图案设计 培优练习(含答案)
文档属性
| 名称 | 3.4 简单的图案设计 培优练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 820.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-05 10:31:19 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
3.4简单的图案设计培优练习北师大版2024—2025学年八年级下册
一、选择题
1.下列运动中,能改变图形大小的是( )
A.平移 B.旋转 C.翻折 D.放缩
2.如图,这是4×4的正方形网格,选择一空白小正方形,其与阴影部分组成的图形是中心对称图形的情况有( )
A.1种 B.2种 C.3种 D.4种
3.雪花缓缓飘落,为大地披上了一层白纱.如图所示的雪花图案是一个中心对称图形,将该图案绕着它的中心旋转,使其与自身重合,至少应旋转的角度是( )
A.30° B.45° C.60° D.90°
4.如图中的五角星图案,绕着它的中心O旋转n°后,能与自身重合,则n的值可以是( )
A.60 B.72
C.120 D.150
5.如图,△ABC和△ADE都是等腰直角三角形,∠ACB和∠D都是直角,点C在AE上,△ABC绕着A点经过逆时针旋转后能够与△ADE重合,再将图(1)作为“基本图形”绕着A点经过逆时针旋转得到图(2).两次旋转的角度分别为( )
A.45°,90° B.90°,45° C.60°,30° D.30°,60°
二、填空题
6.图中的风车图案,绕着它的中心O旋转,旋转角至少为 度,旋转后的风车能与自身重合.
7.如图所示的图案由三个叶片组成,绕点O旋转120°后可以和自身重合,若每个叶片的面积为4cm2,∠AOB=120°,则图中阴影部分的面积为 .
8.定义:在平面直角坐标系xOy中,将点P(x,y)变换为Q(4x+2,2y+4),我们把这种变换称为“SS变换”.已知点A(2,3),B(m,2n),C(m+3,2n)经过“SS变换”的对应点分别是D,E,F.若S三角形AEF=12,则n= .
9.如图,把图中的△ABC经过一定的变换得到△A'B'C',如果图中△ABC上的点P的坐标为(a,b),那么它的对应点P'的坐标为 .
10.如图1是微信朋友圈的LOGO图案,它是中心对称图形,图2是其示意图,其作图过程为:取正八边形ABCDEFGH中心点O,延长OC,AB交于点M,以OM为半径作⊙O,再延长正八边形其余七边得到⊙O的八等分点.若AB=1,则BM= .
三、解答题
11.如图,在直角坐标系xOy中,边长为2的等边三角形AOC的顶点A、O都在x轴上,顶点C在第二象限内,△AOC经过平移或轴对称或旋转都可以得到△OBD.
(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是 个长度单位;△AOC与△BOD关于直线对称,则对称轴是 ;△AOC绕原点O顺时针方向旋转得到△DOB,则旋转角度可以是 度.
(2)连接AD,交OC于点E,求∠AEO的度数.
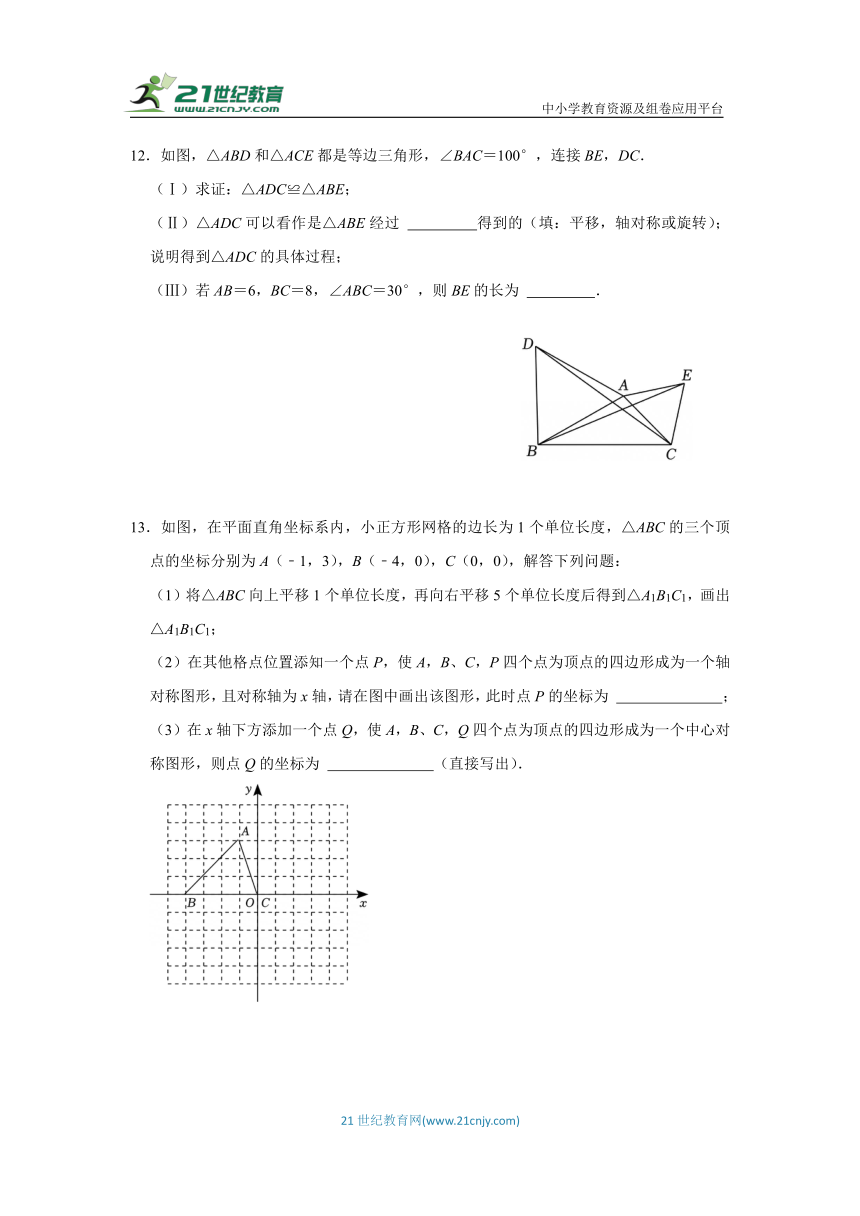
12.如图,△ABD和△ACE都是等边三角形,∠BAC=100°,连接BE,DC.
(Ⅰ)求证:△ADC≌△ABE;
(Ⅱ)△ADC可以看作是△ABE经过 得到的(填:平移,轴对称或旋转);说明得到△ADC的具体过程;
(Ⅲ)若AB=6,BC=8,∠ABC=30°,则BE的长为 .
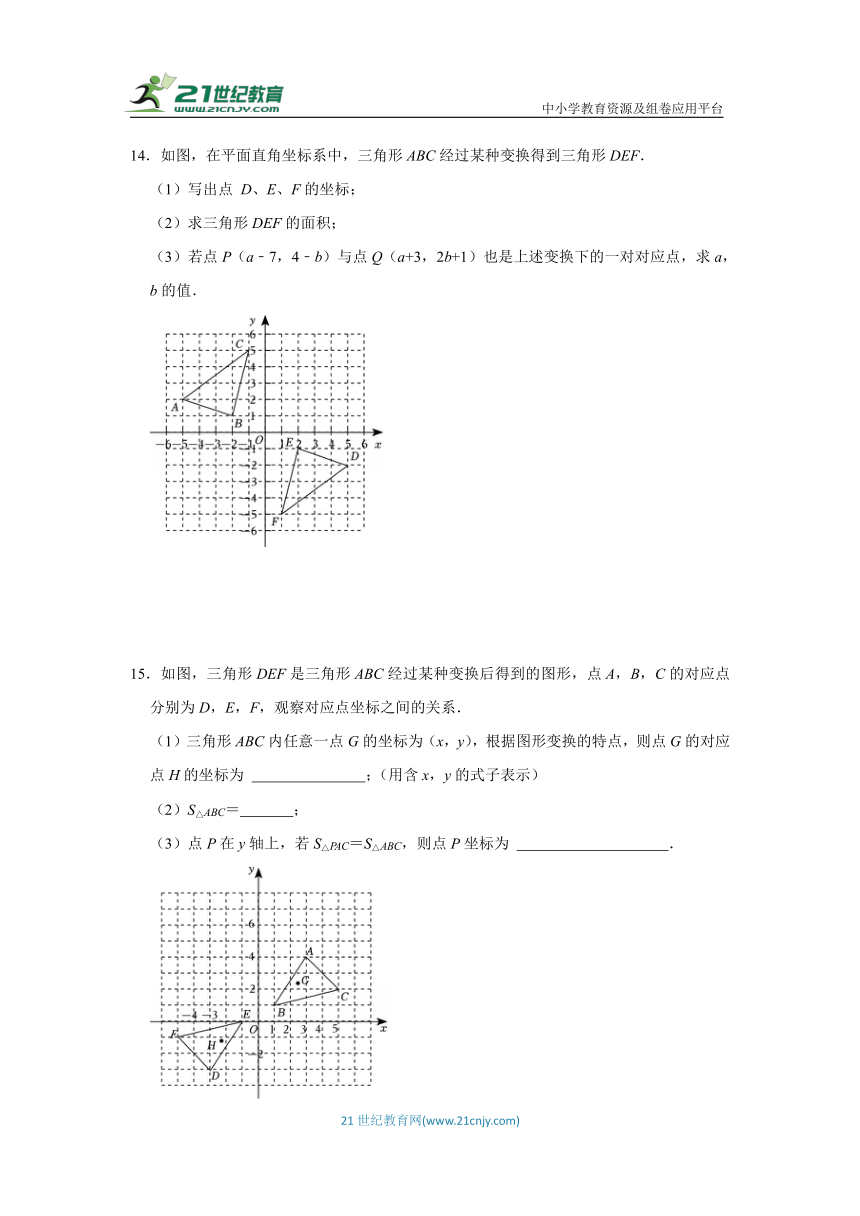
13.如图,在平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(﹣1,3),B(﹣4,0),C(0,0),解答下列问题:
(1)将△ABC向上平移1个单位长度,再向右平移5个单位长度后得到△A1B1C1,画出△A1B1C1;
(2)在其他格点位置添知一个点P,使A,B、C,P四个点为顶点的四边形成为一个轴对称图形,且对称轴为x轴,请在图中画出该图形,此时点P的坐标为 ;
(3)在x轴下方添加一个点Q,使A,B、C,Q四个点为顶点的四边形成为一个中心对称图形,则点Q的坐标为 (直接写出).
14.如图,在平面直角坐标系中,三角形ABC经过某种变换得到三角形DEF.
(1)写出点 D、E、F的坐标;
(2)求三角形DEF的面积;
(3)若点P(a﹣7,4﹣b)与点Q(a+3,2b+1)也是上述变换下的一对对应点,求a,b的值.
15.如图,三角形DEF是三角形ABC经过某种变换后得到的图形,点A,B,C的对应点分别为D,E,F,观察对应点坐标之间的关系.
(1)三角形ABC内任意一点G的坐标为(x,y),根据图形变换的特点,则点G的对应点H的坐标为 ;(用含x,y的式子表示)
(2)S△ABC= ;
(3)点P在y轴上,若S△PAC=S△ABC,则点P坐标为 .
参考答案
一、选择题
题号 1 2 3 4 5
答案 D B C B A
二、填空题
6.【解答】解:该图形被平分成四部分,旋转90度的整数倍,就可以与自身重合,旋转角至少为90°.
故答案为:90.
7.【解答】解:∵每个叶片的面积为4cm2,
∴图形的面积是12cm2,
∵图案绕点O旋转120°后可以和自身重合,∠AOB=120°,
∴图形中阴影部分的面积是图形的面积的 ,
∴图中阴影部分的面积之和为4cm2.
故答案为:4.
8.【解答】解:∵B(m,2n),C(m+3,2n)经过“SS变换”的对应点为E,F,
∴E(4m+2,4n+4),F(4m+14,4n+4),
∴EF∥x轴,
∴EF=12,
∵S三角形AEF=12,
∴EF |4n+4﹣3|=12,
解得n或,
故答案为:或.
9.【解答】解:由图可知,△ABC与△A'B'C'关于点(1.5,0)对称,
设点P'的坐标为(x,y),
∴1.5,0,
解得x=3﹣a,y=﹣b,
∴P'(3﹣a,﹣b).
故答案为:(3﹣a,﹣b).
10.【解答】解:如图,过点O作OH⊥AB于点H,过点B作BJ⊥OA于点J.
正八边形ABCDEFGH中,OA=OB,AB=1,∠BOA=∠BOC=45°,
∵BJ⊥OA,
∴OJ=BJOB,
设BJ=OJ=x,则OB=OAx,
∴AJ=OA﹣OJx﹣x,
∵JA2+BJ2=AB2,
∴(x﹣x)2+x2=12,
∴x2,
∵∠AOB=∠BOC=45°,
∴∠AOM=90°,
∵OH⊥AB,
∴AH=BH,
∵∠OAH=∠MAO,∠AHO=∠AOM=90°,
∴△AOH∽△AMO,
∴,
∴OA2=AH AM,
∴AM2,
∴BM=AM﹣AB=21=1.
故答案为:1.
三、解答题
11.【解答】解:(1)△AOC沿数轴向右平移得到△OBD,则平移的距离是2个单位长度;△AOC与△BOD关于直线对称,则对称轴是y轴;△AOC绕原点O顺时针旋转得到△DOB,则旋转角度至少是120°度,
故答案为:2;y轴;120;
(2)∵△AOC和△DOB是能够重合的等边三角形,
∴AO=DO,∠AOC=∠COD=60°,
∴OE⊥AD,
∴∠AEO=90°.
12.【解答】(Ⅰ)证明:∵△ABD和△ACE都是等边三角形,
∴AB=AD,AC=AE,∠BAD=∠CAE=60°,
∴∠DAC=∠BAE,\
在△ADC和△BAE中,
,
∴△ADC≌△ABE(SAS);
(Ⅱ)解:将△ABE绕点A顺时针旋转60°得到△ADC.
故答案为:旋转;
(Ⅲ)解:∵△ABD是等边三角形,
∴BD=AB=6,∠ABD=60°,
∵∠ABC=30°,
∴∠DBC=∠ABD+∠ABC=90°,
∴CD10,
∵△ADC≌△ABE,
∴CD=BE=10.
故答案为:10.
13.【解答】解:(1)如图,△A1B1C1;即为所求;
(2)如图,点P即为所求,P(﹣1,﹣3).
故答案为:(﹣1,﹣3);
(3)如图,点Q即为所求,Q(﹣3,﹣3).
14.【解答】解:(1)点 D(5,﹣2)、E(2,﹣1)、F(1,﹣5);
(2)三角形DEF的面积=4×41×41×33×4=6.5;
(3)由图形可知,△ABC与△DEF关于原点对称,
∴a﹣7+a+3=0,4﹣b+2b+1=0,
∴a=2,b=﹣5.
15.【解答】解:(1)由图可知:△ABC和△DEF是关于对称,
故点G、H关于对称,
∴,即,
∴,
∴点H(﹣x,1﹣y),
(2),
(3)
∵S△APC=S△ABC,
∴点P到AC的距离与点B到AC的距离相等,
∴BP∥AC,
∵点P在y轴上,如图,过B点作AC的平行线可知与y轴交点就是P点坐标,
∴P(0,2).
又∵点B(1,1)关于AC对称点B'(6,6),如图,过B′点作AC的平行线可知与y轴交点就是P点坐标,
∴P(0,12).
故P坐标为P(0,2)或P(0,12).
故答案为:(0,2)或(0,12).
21世纪教育网(www.21cnjy.com)
3.4简单的图案设计培优练习北师大版2024—2025学年八年级下册
一、选择题
1.下列运动中,能改变图形大小的是( )
A.平移 B.旋转 C.翻折 D.放缩
2.如图,这是4×4的正方形网格,选择一空白小正方形,其与阴影部分组成的图形是中心对称图形的情况有( )
A.1种 B.2种 C.3种 D.4种
3.雪花缓缓飘落,为大地披上了一层白纱.如图所示的雪花图案是一个中心对称图形,将该图案绕着它的中心旋转,使其与自身重合,至少应旋转的角度是( )
A.30° B.45° C.60° D.90°
4.如图中的五角星图案,绕着它的中心O旋转n°后,能与自身重合,则n的值可以是( )
A.60 B.72
C.120 D.150
5.如图,△ABC和△ADE都是等腰直角三角形,∠ACB和∠D都是直角,点C在AE上,△ABC绕着A点经过逆时针旋转后能够与△ADE重合,再将图(1)作为“基本图形”绕着A点经过逆时针旋转得到图(2).两次旋转的角度分别为( )
A.45°,90° B.90°,45° C.60°,30° D.30°,60°
二、填空题
6.图中的风车图案,绕着它的中心O旋转,旋转角至少为 度,旋转后的风车能与自身重合.
7.如图所示的图案由三个叶片组成,绕点O旋转120°后可以和自身重合,若每个叶片的面积为4cm2,∠AOB=120°,则图中阴影部分的面积为 .
8.定义:在平面直角坐标系xOy中,将点P(x,y)变换为Q(4x+2,2y+4),我们把这种变换称为“SS变换”.已知点A(2,3),B(m,2n),C(m+3,2n)经过“SS变换”的对应点分别是D,E,F.若S三角形AEF=12,则n= .
9.如图,把图中的△ABC经过一定的变换得到△A'B'C',如果图中△ABC上的点P的坐标为(a,b),那么它的对应点P'的坐标为 .
10.如图1是微信朋友圈的LOGO图案,它是中心对称图形,图2是其示意图,其作图过程为:取正八边形ABCDEFGH中心点O,延长OC,AB交于点M,以OM为半径作⊙O,再延长正八边形其余七边得到⊙O的八等分点.若AB=1,则BM= .
三、解答题
11.如图,在直角坐标系xOy中,边长为2的等边三角形AOC的顶点A、O都在x轴上,顶点C在第二象限内,△AOC经过平移或轴对称或旋转都可以得到△OBD.
(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是 个长度单位;△AOC与△BOD关于直线对称,则对称轴是 ;△AOC绕原点O顺时针方向旋转得到△DOB,则旋转角度可以是 度.
(2)连接AD,交OC于点E,求∠AEO的度数.
12.如图,△ABD和△ACE都是等边三角形,∠BAC=100°,连接BE,DC.
(Ⅰ)求证:△ADC≌△ABE;
(Ⅱ)△ADC可以看作是△ABE经过 得到的(填:平移,轴对称或旋转);说明得到△ADC的具体过程;
(Ⅲ)若AB=6,BC=8,∠ABC=30°,则BE的长为 .
13.如图,在平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(﹣1,3),B(﹣4,0),C(0,0),解答下列问题:
(1)将△ABC向上平移1个单位长度,再向右平移5个单位长度后得到△A1B1C1,画出△A1B1C1;
(2)在其他格点位置添知一个点P,使A,B、C,P四个点为顶点的四边形成为一个轴对称图形,且对称轴为x轴,请在图中画出该图形,此时点P的坐标为 ;
(3)在x轴下方添加一个点Q,使A,B、C,Q四个点为顶点的四边形成为一个中心对称图形,则点Q的坐标为 (直接写出).
14.如图,在平面直角坐标系中,三角形ABC经过某种变换得到三角形DEF.
(1)写出点 D、E、F的坐标;
(2)求三角形DEF的面积;
(3)若点P(a﹣7,4﹣b)与点Q(a+3,2b+1)也是上述变换下的一对对应点,求a,b的值.
15.如图,三角形DEF是三角形ABC经过某种变换后得到的图形,点A,B,C的对应点分别为D,E,F,观察对应点坐标之间的关系.
(1)三角形ABC内任意一点G的坐标为(x,y),根据图形变换的特点,则点G的对应点H的坐标为 ;(用含x,y的式子表示)
(2)S△ABC= ;
(3)点P在y轴上,若S△PAC=S△ABC,则点P坐标为 .
参考答案
一、选择题
题号 1 2 3 4 5
答案 D B C B A
二、填空题
6.【解答】解:该图形被平分成四部分,旋转90度的整数倍,就可以与自身重合,旋转角至少为90°.
故答案为:90.
7.【解答】解:∵每个叶片的面积为4cm2,
∴图形的面积是12cm2,
∵图案绕点O旋转120°后可以和自身重合,∠AOB=120°,
∴图形中阴影部分的面积是图形的面积的 ,
∴图中阴影部分的面积之和为4cm2.
故答案为:4.
8.【解答】解:∵B(m,2n),C(m+3,2n)经过“SS变换”的对应点为E,F,
∴E(4m+2,4n+4),F(4m+14,4n+4),
∴EF∥x轴,
∴EF=12,
∵S三角形AEF=12,
∴EF |4n+4﹣3|=12,
解得n或,
故答案为:或.
9.【解答】解:由图可知,△ABC与△A'B'C'关于点(1.5,0)对称,
设点P'的坐标为(x,y),
∴1.5,0,
解得x=3﹣a,y=﹣b,
∴P'(3﹣a,﹣b).
故答案为:(3﹣a,﹣b).
10.【解答】解:如图,过点O作OH⊥AB于点H,过点B作BJ⊥OA于点J.
正八边形ABCDEFGH中,OA=OB,AB=1,∠BOA=∠BOC=45°,
∵BJ⊥OA,
∴OJ=BJOB,
设BJ=OJ=x,则OB=OAx,
∴AJ=OA﹣OJx﹣x,
∵JA2+BJ2=AB2,
∴(x﹣x)2+x2=12,
∴x2,
∵∠AOB=∠BOC=45°,
∴∠AOM=90°,
∵OH⊥AB,
∴AH=BH,
∵∠OAH=∠MAO,∠AHO=∠AOM=90°,
∴△AOH∽△AMO,
∴,
∴OA2=AH AM,
∴AM2,
∴BM=AM﹣AB=21=1.
故答案为:1.
三、解答题
11.【解答】解:(1)△AOC沿数轴向右平移得到△OBD,则平移的距离是2个单位长度;△AOC与△BOD关于直线对称,则对称轴是y轴;△AOC绕原点O顺时针旋转得到△DOB,则旋转角度至少是120°度,
故答案为:2;y轴;120;
(2)∵△AOC和△DOB是能够重合的等边三角形,
∴AO=DO,∠AOC=∠COD=60°,
∴OE⊥AD,
∴∠AEO=90°.
12.【解答】(Ⅰ)证明:∵△ABD和△ACE都是等边三角形,
∴AB=AD,AC=AE,∠BAD=∠CAE=60°,
∴∠DAC=∠BAE,\
在△ADC和△BAE中,
,
∴△ADC≌△ABE(SAS);
(Ⅱ)解:将△ABE绕点A顺时针旋转60°得到△ADC.
故答案为:旋转;
(Ⅲ)解:∵△ABD是等边三角形,
∴BD=AB=6,∠ABD=60°,
∵∠ABC=30°,
∴∠DBC=∠ABD+∠ABC=90°,
∴CD10,
∵△ADC≌△ABE,
∴CD=BE=10.
故答案为:10.
13.【解答】解:(1)如图,△A1B1C1;即为所求;
(2)如图,点P即为所求,P(﹣1,﹣3).
故答案为:(﹣1,﹣3);
(3)如图,点Q即为所求,Q(﹣3,﹣3).
14.【解答】解:(1)点 D(5,﹣2)、E(2,﹣1)、F(1,﹣5);
(2)三角形DEF的面积=4×41×41×33×4=6.5;
(3)由图形可知,△ABC与△DEF关于原点对称,
∴a﹣7+a+3=0,4﹣b+2b+1=0,
∴a=2,b=﹣5.
15.【解答】解:(1)由图可知:△ABC和△DEF是关于对称,
故点G、H关于对称,
∴,即,
∴,
∴点H(﹣x,1﹣y),
(2),
(3)
∵S△APC=S△ABC,
∴点P到AC的距离与点B到AC的距离相等,
∴BP∥AC,
∵点P在y轴上,如图,过B点作AC的平行线可知与y轴交点就是P点坐标,
∴P(0,2).
又∵点B(1,1)关于AC对称点B'(6,6),如图,过B′点作AC的平行线可知与y轴交点就是P点坐标,
∴P(0,12).
故P坐标为P(0,2)或P(0,12).
故答案为:(0,2)或(0,12).
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
