第六章平行四边形单元测试北师大版2024—2025学年八年级下册(含答案)
文档属性
| 名称 | 第六章平行四边形单元测试北师大版2024—2025学年八年级下册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 636.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-05 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第六章平行四边形单元测试北师大版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.小宇看到一个多边形中,从某一顶点出发的对角线共有3条,那么这个多边形的内角和是( )
A.720° B.540° C.360° D.180°
2.一个多边形的内角和是外角和的4倍,则这个多边形是( )
A.七边形 B.八边形 C.九边形 D.十边形
3.如图,∠A+∠B+∠C+∠D+∠E的度数为( )
A.180° B.240° C.270° D.360°
4.如图,在△ABC中,BA=BC=5,AC=6,点D,点E分别是BC,AB边上的动点,连结DE,点F,点M分别是CD,DE的中点,则FM的最小值为( )
A. B. C.3 D.
5.如图,在 ABCD中,对角线AC,BD交于点O.E是CD的中点,连结BE交AC于点F.若 ABCD的面积为36,则△BOF的面积为( )
A.2 B.3 C.4 D.5
6.如图,四边形ABCD的对角线AC,BD交于点O,则不能判断四边形ABCD是平行四边形的是( )
A.∠ABD=∠BDC,OA=OC B.∠ABC=∠ADC,AB=CD
C.AD∥BC,OB=OD D.∠ABD=∠BDC,∠ADB=∠CBD
7.如图,在 ABCD中,AE⊥BC于点E,AF⊥CD于点F.若AE=4,AF=6,且 ABCD的周长为40,则 ABCD的面积为( )
A.24 B.36 C.40 D.48
8.如图,在△ABC中,AB=3,AC=4,BC=5,△ABD,△ACE,△BCF都是等边三角形,下列结论中:①AB⊥AC;②△DBF≌△ABC;③四边形AEFD是平行四边形;
④∠DFE=110°;⑤S四边形AEFD=5.正确的个数是( )
A.2个 B.3个 C.4个 D.5个
二.填空题(每小题5分,满分20分)
9.如果一个正多边形的内角和为1800°,那么这个正多边形共有对角线 条.
10.如图,由正方形、正五边形、正六边形组合而成的图形中,∠2+∠3=110°,
则∠1= 度.
11.如图,在 ABCD中,对角线AC,BD交于点O,AC⊥CD,过点O作OE⊥AC交AD于点E,连接CE.已知AC=6,BD=10,则△CDE的周长是 .
12.如图,在△ABC中,AB=8,点D、E分别是边AB、AC的中点,点F是线段DE上的一点且EF=2,连接AF、BF,若∠AFB=90°,则线段BC的长为 .
三.解答题(共6小题,每小题10分,每题须有必要的文字说明和解答过程)
13.如图,在平行四边形ABCD中,对角线AC和BD交于点O,点E、F分别为OA、OC的中点,连接BE、DF.
(1)求证:△ABE≌△CDF;
(2)若BD=2AB,且AB=20,CF=12,求DF的长.
14.如图,在Rt△ABC中,∠BAC=90°,E,F分别是BC,AC的中点,延长BA到点D,使,连结DE,DF,DE交AF于点M.
(1)求证:AP=FP;
(2)若BC=10,求DF的长.
15.已知一个多边形的边数为n.
(1)若n=6,求这个多边形的内角和;
(2)若这个多边形的内角和是它的外角和的3倍,求n的值.
16.如图,把△ABC的纸片沿着DE折叠.
(1)若点A落在四边形BCDE的内部点A′的位置(如图1),且∠1=40°,∠2=24°,请求出∠A′的度数;
(2)若点A落在四边形BCDE的外部BE的上方点A′的位置(如图2),求证:.
17.如图,在△ABC中,AB=AC,将△ABC绕点A沿逆时针方向旋转得到△ADE,BD与CE交于点F.
(1)若∠BCF=25°,求∠EDF的度数;
(2)若AB=1,∠BAC=45°,当四边形ADFC是平行四边形时,求∠BAE的度数及EC的长.
18.如图,等边△ABC的边长是4,D,E分别为AB,AC的中点,延长BC至点F,使CFBC,连接CD和EF.
(1)求证:DE=CF;
(2)求EF的长;
(3)求四边形DEFC的面积.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8
答案 A D A A B B D B
二、填空题
9.【解答】解:设该正多边形的边数为n,根据多边形的内角和定理可得:
(n﹣2) 180°=1800°,
解得:n=12,
∴对角线为:(条),
故答案为:54.
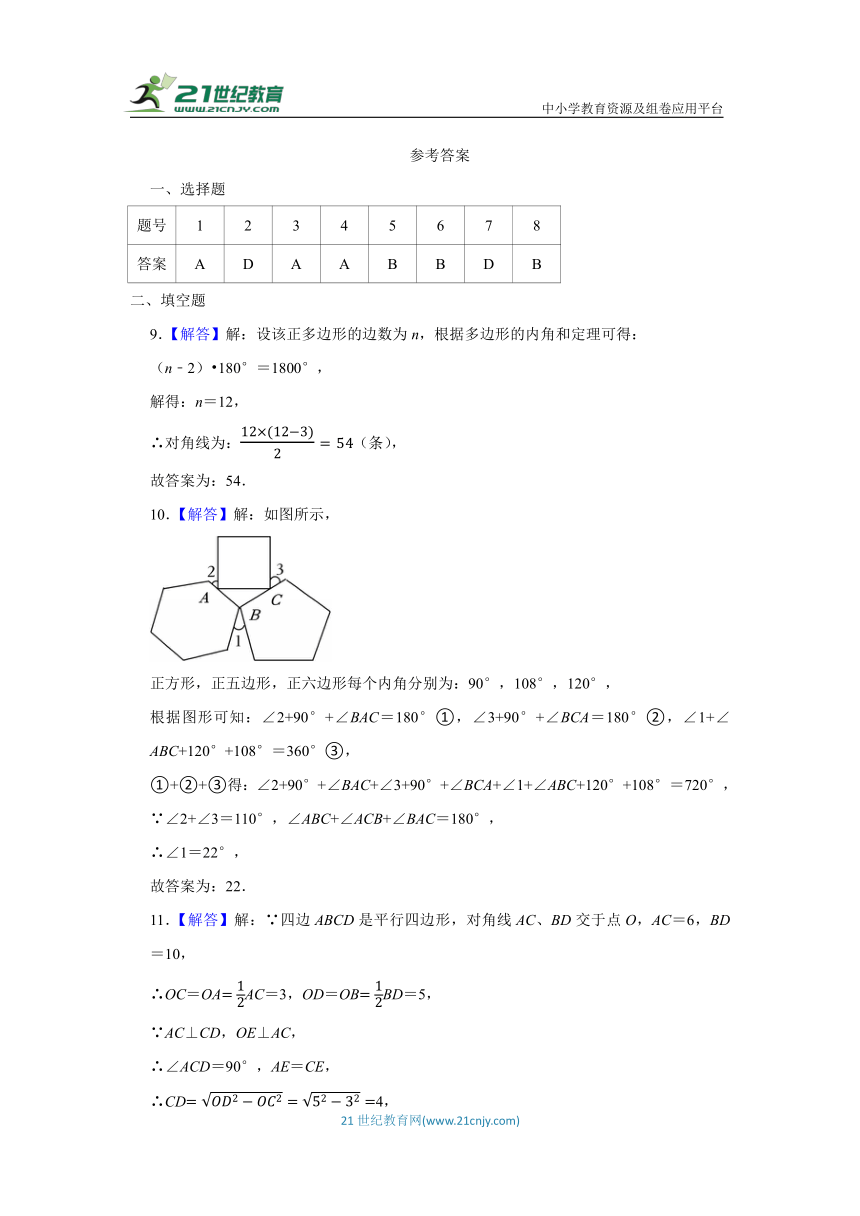
10.【解答】解:如图所示,
正方形,正五边形,正六边形每个内角分别为:90°,108°,120°,
根据图形可知:∠2+90°+∠BAC=180°①,∠3+90°+∠BCA=180°②,∠1+∠ABC+120°+108°=360°③,
①+②+③得:∠2+90°+∠BAC+∠3+90°+∠BCA+∠1+∠ABC+120°+108°=720°,
∵∠2+∠3=110°,∠ABC+∠ACB+∠BAC=180°,
∴∠1=22°,
故答案为:22.
11.【解答】解:∵四边ABCD是平行四边形,对角线AC、BD交于点O,AC=6,BD=10,
∴OC=OAAC=3,OD=OBBD=5,
∵AC⊥CD,OE⊥AC,
∴∠ACD=90°,AE=CE,
∴CD4,
∴AD2,
∵∠ECD+∠ECA=90°,∠EDC+∠EAC=90°,∠ECA=∠EAC,
∴∠ECD=∠EDC,
∴DE=CE=AEAD,
∴△CDE的周长=CD+DE+CE=44+2,
∴故答案为:4+2.
12.【解答】解:∵点D、E分别是边AB、AC的中点,
∴DE是△ABC的中位线,
∴DEBC,
∵∠AFB=90°,D是AB的中点,AB=8,
∴DFAB8=4,
∵EF=2.
∴DE=EF+DF=6.
∴BC=12,
故答案为:12.
三、解答题
13.【解答】(1)证明:∵平行四边形ABCD,
∴AB=CD,OA=OC,AB∥CD,
∴∠BAE=∠DCF,
∵点E,F分别为OA,OC的中点,
∴,,
∴AE=CF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS);
(2)解:∵BD=2AB,且AB=20,CF=12,
∴BD=40,
∵四边形ABCD是平行四边形,
∴,
∴△DCO为等腰三角形,
∵点F是CO的中点,
∴DF⊥AC,
在Rt△CDF中,CF=12,CD=20,
由勾股定理得:.
14.【解答】(1)证明:连接EF,AE.
∵点E,F分别为BC,AC的中点,
∴EF∥AB,EFAB.
又∵ADAB,
∴EF=AD.
又∵EF∥AD,
∴四边形AEFD是平行四边形.
∴AF与DE互相平分,
∴AP=FP;
(2)解:在Rt△ABC中,
∵E为BC的中点,BC=10,
∴AEBC=5.
又∵四边形AEFD是平行四边形,
∴DF=AE=5.
15.【解答】解:(1)当n=6时,(6﹣2)×180°=720°,
所以这个多边形的内角和为720°;
(2)由题意得,(n﹣2)×180°=360°×3,
解得:n=8,
所以n的值为8.
16.【解答】解:(1)由折叠的性质得∠A=∠A′,∠ADE=∠A′DE,∠AED=∠A′ED
由条件可知∠ADE=∠A′DE=70°,∠2+∠AED+∠A′ED=180°,∠2=24°,
∴∠AED=∠A′ED=78°,
∴∠A′=180°﹣∠A′DE﹣∠A′ED=32°;
(2)∵∠ADE+∠A′DE+∠2=180°,
∴,
∴,
∴,
∴,
∴∠1=∠2﹣2∠A,
∴∠1=∠2﹣2∠A′,即.
17.【解答】解:(1)连接BE.
∵将△ABC绕点A沿顺时针旋转得到△ADE,
∴AD=AB,AC=AE,∠BAC=∠DAE,
∴∠DAB=∠EAC,
又∵AB=AC,AD=AB,AC=AE,
∴AD=AE,
在△AEC和△ADB中,
,
∴△AEC≌△ADB(SAS),
∴EC=BD.
在△DEB和△CBE中,
,
∴△DEB≌△CBE(SSS).
∴∠EDF=∠ECB=25°;
(2)由旋转性质得∠DAE=BAC=45°,AB=AC=AD=AE=1,
∵四边形ADFC是平行四边形,
∴AC∥DF.
∴∠ABD=∠BAC=45°,
∵AD=AB=1,
∴∠ADB=∠ABD=45°.
∴∠DAB=90°.
∵∠BAC=∠DAE=45°,
∴∠BAE=45°
由勾股定理,可求得,
∵△AEC≌△ADB,
∴.
18.【解答】解:(1)在△ABC中,
∵D、E分别为AB、AC的中点,
∴DE为△ABC的中位线,
∴DEBC,
∵CFBC,
∴DE=CF.
(2)∵AC=BC,AD=BD,
∴CD⊥AB,
∵BC=4,BD=2,
∴CD2,
∵DE∥CF,DE=CF,
∴四边形DEFC是平行四边形,
∴EF=CD=2.
(3)过点D作DH⊥BC于H.
∵∠DHC=90°,∠DCB=30°,
∴DHDC,
∵DE=CF=2,
∴S四边形DEFC=CF DH=22.
21世纪教育网(www.21cnjy.com)
第六章平行四边形单元测试北师大版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.小宇看到一个多边形中,从某一顶点出发的对角线共有3条,那么这个多边形的内角和是( )
A.720° B.540° C.360° D.180°
2.一个多边形的内角和是外角和的4倍,则这个多边形是( )
A.七边形 B.八边形 C.九边形 D.十边形
3.如图,∠A+∠B+∠C+∠D+∠E的度数为( )
A.180° B.240° C.270° D.360°
4.如图,在△ABC中,BA=BC=5,AC=6,点D,点E分别是BC,AB边上的动点,连结DE,点F,点M分别是CD,DE的中点,则FM的最小值为( )
A. B. C.3 D.
5.如图,在 ABCD中,对角线AC,BD交于点O.E是CD的中点,连结BE交AC于点F.若 ABCD的面积为36,则△BOF的面积为( )
A.2 B.3 C.4 D.5
6.如图,四边形ABCD的对角线AC,BD交于点O,则不能判断四边形ABCD是平行四边形的是( )
A.∠ABD=∠BDC,OA=OC B.∠ABC=∠ADC,AB=CD
C.AD∥BC,OB=OD D.∠ABD=∠BDC,∠ADB=∠CBD
7.如图,在 ABCD中,AE⊥BC于点E,AF⊥CD于点F.若AE=4,AF=6,且 ABCD的周长为40,则 ABCD的面积为( )
A.24 B.36 C.40 D.48
8.如图,在△ABC中,AB=3,AC=4,BC=5,△ABD,△ACE,△BCF都是等边三角形,下列结论中:①AB⊥AC;②△DBF≌△ABC;③四边形AEFD是平行四边形;
④∠DFE=110°;⑤S四边形AEFD=5.正确的个数是( )
A.2个 B.3个 C.4个 D.5个
二.填空题(每小题5分,满分20分)
9.如果一个正多边形的内角和为1800°,那么这个正多边形共有对角线 条.
10.如图,由正方形、正五边形、正六边形组合而成的图形中,∠2+∠3=110°,
则∠1= 度.
11.如图,在 ABCD中,对角线AC,BD交于点O,AC⊥CD,过点O作OE⊥AC交AD于点E,连接CE.已知AC=6,BD=10,则△CDE的周长是 .
12.如图,在△ABC中,AB=8,点D、E分别是边AB、AC的中点,点F是线段DE上的一点且EF=2,连接AF、BF,若∠AFB=90°,则线段BC的长为 .
三.解答题(共6小题,每小题10分,每题须有必要的文字说明和解答过程)
13.如图,在平行四边形ABCD中,对角线AC和BD交于点O,点E、F分别为OA、OC的中点,连接BE、DF.
(1)求证:△ABE≌△CDF;
(2)若BD=2AB,且AB=20,CF=12,求DF的长.
14.如图,在Rt△ABC中,∠BAC=90°,E,F分别是BC,AC的中点,延长BA到点D,使,连结DE,DF,DE交AF于点M.
(1)求证:AP=FP;
(2)若BC=10,求DF的长.
15.已知一个多边形的边数为n.
(1)若n=6,求这个多边形的内角和;
(2)若这个多边形的内角和是它的外角和的3倍,求n的值.
16.如图,把△ABC的纸片沿着DE折叠.
(1)若点A落在四边形BCDE的内部点A′的位置(如图1),且∠1=40°,∠2=24°,请求出∠A′的度数;
(2)若点A落在四边形BCDE的外部BE的上方点A′的位置(如图2),求证:.
17.如图,在△ABC中,AB=AC,将△ABC绕点A沿逆时针方向旋转得到△ADE,BD与CE交于点F.
(1)若∠BCF=25°,求∠EDF的度数;
(2)若AB=1,∠BAC=45°,当四边形ADFC是平行四边形时,求∠BAE的度数及EC的长.
18.如图,等边△ABC的边长是4,D,E分别为AB,AC的中点,延长BC至点F,使CFBC,连接CD和EF.
(1)求证:DE=CF;
(2)求EF的长;
(3)求四边形DEFC的面积.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8
答案 A D A A B B D B
二、填空题
9.【解答】解:设该正多边形的边数为n,根据多边形的内角和定理可得:
(n﹣2) 180°=1800°,
解得:n=12,
∴对角线为:(条),
故答案为:54.
10.【解答】解:如图所示,
正方形,正五边形,正六边形每个内角分别为:90°,108°,120°,
根据图形可知:∠2+90°+∠BAC=180°①,∠3+90°+∠BCA=180°②,∠1+∠ABC+120°+108°=360°③,
①+②+③得:∠2+90°+∠BAC+∠3+90°+∠BCA+∠1+∠ABC+120°+108°=720°,
∵∠2+∠3=110°,∠ABC+∠ACB+∠BAC=180°,
∴∠1=22°,
故答案为:22.
11.【解答】解:∵四边ABCD是平行四边形,对角线AC、BD交于点O,AC=6,BD=10,
∴OC=OAAC=3,OD=OBBD=5,
∵AC⊥CD,OE⊥AC,
∴∠ACD=90°,AE=CE,
∴CD4,
∴AD2,
∵∠ECD+∠ECA=90°,∠EDC+∠EAC=90°,∠ECA=∠EAC,
∴∠ECD=∠EDC,
∴DE=CE=AEAD,
∴△CDE的周长=CD+DE+CE=44+2,
∴故答案为:4+2.
12.【解答】解:∵点D、E分别是边AB、AC的中点,
∴DE是△ABC的中位线,
∴DEBC,
∵∠AFB=90°,D是AB的中点,AB=8,
∴DFAB8=4,
∵EF=2.
∴DE=EF+DF=6.
∴BC=12,
故答案为:12.
三、解答题
13.【解答】(1)证明:∵平行四边形ABCD,
∴AB=CD,OA=OC,AB∥CD,
∴∠BAE=∠DCF,
∵点E,F分别为OA,OC的中点,
∴,,
∴AE=CF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS);
(2)解:∵BD=2AB,且AB=20,CF=12,
∴BD=40,
∵四边形ABCD是平行四边形,
∴,
∴△DCO为等腰三角形,
∵点F是CO的中点,
∴DF⊥AC,
在Rt△CDF中,CF=12,CD=20,
由勾股定理得:.
14.【解答】(1)证明:连接EF,AE.
∵点E,F分别为BC,AC的中点,
∴EF∥AB,EFAB.
又∵ADAB,
∴EF=AD.
又∵EF∥AD,
∴四边形AEFD是平行四边形.
∴AF与DE互相平分,
∴AP=FP;
(2)解:在Rt△ABC中,
∵E为BC的中点,BC=10,
∴AEBC=5.
又∵四边形AEFD是平行四边形,
∴DF=AE=5.
15.【解答】解:(1)当n=6时,(6﹣2)×180°=720°,
所以这个多边形的内角和为720°;
(2)由题意得,(n﹣2)×180°=360°×3,
解得:n=8,
所以n的值为8.
16.【解答】解:(1)由折叠的性质得∠A=∠A′,∠ADE=∠A′DE,∠AED=∠A′ED
由条件可知∠ADE=∠A′DE=70°,∠2+∠AED+∠A′ED=180°,∠2=24°,
∴∠AED=∠A′ED=78°,
∴∠A′=180°﹣∠A′DE﹣∠A′ED=32°;
(2)∵∠ADE+∠A′DE+∠2=180°,
∴,
∴,
∴,
∴,
∴∠1=∠2﹣2∠A,
∴∠1=∠2﹣2∠A′,即.
17.【解答】解:(1)连接BE.
∵将△ABC绕点A沿顺时针旋转得到△ADE,
∴AD=AB,AC=AE,∠BAC=∠DAE,
∴∠DAB=∠EAC,
又∵AB=AC,AD=AB,AC=AE,
∴AD=AE,
在△AEC和△ADB中,
,
∴△AEC≌△ADB(SAS),
∴EC=BD.
在△DEB和△CBE中,
,
∴△DEB≌△CBE(SSS).
∴∠EDF=∠ECB=25°;
(2)由旋转性质得∠DAE=BAC=45°,AB=AC=AD=AE=1,
∵四边形ADFC是平行四边形,
∴AC∥DF.
∴∠ABD=∠BAC=45°,
∵AD=AB=1,
∴∠ADB=∠ABD=45°.
∴∠DAB=90°.
∵∠BAC=∠DAE=45°,
∴∠BAE=45°
由勾股定理,可求得,
∵△AEC≌△ADB,
∴.
18.【解答】解:(1)在△ABC中,
∵D、E分别为AB、AC的中点,
∴DE为△ABC的中位线,
∴DEBC,
∵CFBC,
∴DE=CF.
(2)∵AC=BC,AD=BD,
∴CD⊥AB,
∵BC=4,BD=2,
∴CD2,
∵DE∥CF,DE=CF,
∴四边形DEFC是平行四边形,
∴EF=CD=2.
(3)过点D作DH⊥BC于H.
∵∠DHC=90°,∠DCB=30°,
∴DHDC,
∵DE=CF=2,
∴S四边形DEFC=CF DH=22.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
