2025年浙江省小升初数学近三年真题分类汇编专题05 选择题50题(含答案)
文档属性
| 名称 | 2025年浙江省小升初数学近三年真题分类汇编专题05 选择题50题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 669.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-03 21:30:42 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025年浙江省小升初数学近三年真题分类汇编
专题05 选择题50题
一、单选题
1.(2024·浙江)原价每袋2元的某种牛奶,甲、乙、丙三店均在搞促销活动,甲商店每袋降价16%,乙商店“买四送一”,丙商店每袋打9折出售,小明要买5袋牛奶,应从( )商店购买比较便宜.
A.甲 B.乙 C.丙 D.三店均可
2.(2023·海曙)丁丁在肯德基订餐,他的订餐号是一个四位数,左起第一位是最小的自然数,第二位是最小的质数,第三位既是奇数又是合数,第四位是自然数的计数单位,他的订餐号是( )
A.1920 B.1390 C.0291 D.0231
3.(2023两江巴蜀)不是发生在闰年的大事是( )。
A.2008年神舟七号载人飞船成功发射
B.2016年中国女排重夺奥运冠军
C.2010年上海世博会举办
D.2020年我国再次完成珠峰测高任务
4.(2023·柯城)甲仓货存量比乙仓多20%,乙仓货存量比丙仓少20%,那么货存量( )
A.甲仓最多 B.乙仓最多 C.丙仓最多 D.无法判断
5.(2023·柯城)2020年的1月份、2月份、3月份一共有( )天。
A.89 B.90 C.91 D.92
6.(2023·柯城)修一条水渠,计划每天修80m,20天可以完成,如果要提前4天完成,那么每天要比计划多修( )米。
A.20 B.60 C.64 D.100
7.(2023·柯城)王老师家的电表七月抄表数是240度,八月抄表数是501度,已知家用电的价格是每度x元,那么王老师家七月应该缴纳电费( )元。
A.501x B.261x C.240x D.741x
8.(2023·柯城)把1米长的铁丝截成每段长米的小段,要截( )次。
A.3 B.4 C.5 D.6
9.(2023六下·海曙)下列说法正确的是( )。
A.从0~9这10张数字卡片中,任意抽取1张,抽到比5大的数字的可能性比较大
B.一个笔盒提价20%后又降价20%,价格不变。
C.表示一周内气温的变化情况,选用折线统计图比较合适。
D.所有的偶数都是合数。
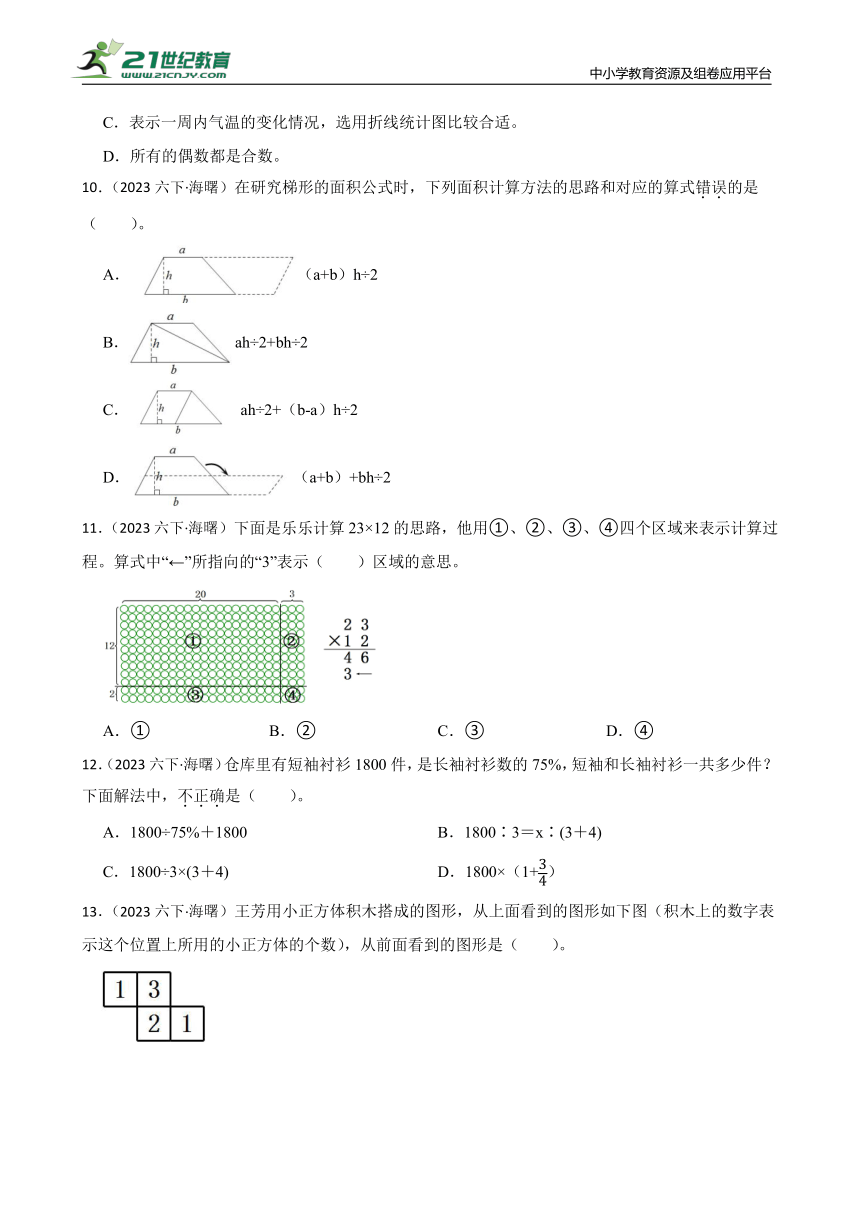
10.(2023六下·海曙)在研究梯形的面积公式时,下列面积计算方法的思路和对应的算式错误的是( )。
A.(a+b)h÷2
B.ah÷2+bh÷2
C.ah÷2+(b-a)h÷2
D.(a+b)+bh÷2
11.(2023六下·海曙)下面是乐乐计算23×12的思路,他用①、②、③、④四个区域来表示计算过程。算式中“←”所指向的“3”表示( )区域的意思。
A.① B.② C.③ D.④
12.(2023六下·海曙)仓库里有短袖衬衫1800件,是长袖衬衫数的75%,短袖和长袖衬衫一共多少件?下面解法中,不正确是( )。
A.1800÷75%+1800 B.1800∶3=x∶(3+4)
C.1800÷3×(3+4) D.1800×(1+)
13.(2023六下·海曙)王芳用小正方体积木搭成的图形,从上面看到的图形如下图(积木上的数字表示这个位置上所用的小正方体的个数),从前面看到的图形是( )。
A. B.
C. D.
14.(2023六下·海曙)浙江省的占地面积约105500平方千米,宁波市的面积大约是( )平方千米。
A.50000 B.20000 C.10000 D.5000
15.(2023六下·海曙)魏晋时期的数学家刘徽从圆内接正六边形开始,将边数逐次加倍,得到的圆内接正多边形就逐步逼近圆,为此来计算圆的周长、面积以及圆周率。这种方法称为( )。
A.刘徽法 B.近圆术 C.圆中方 D.割圆术
16.(2023六下·海曙)象棋规则口诀中有“马走日”、“象走田”的说法。在下面的棋局中,如果用“象”吃掉对方的“兵”,应该向( )方向走。
A.西北 B.东北 C.西南 D.东南
17.(2023六下·海曙)下面各数中“8”表示的意义不同的是( )。
A.0.80 B. C.8% D.0.08
18.(2023·宁波)下面四个数都是六位数,N是比10小的自然数,S是0,一定能被3和5整除的数是( )
A.NNNSNN B.NSNSNS C.NSSNSS D.NSSNSN
19.(2020·慈溪)根据三角形三个角的度数,判断下面三角形中对称轴最多的是( )
A.60°,60°,60° B.90°,45°,45°
C.90°,60°,30° D.120°,40°,20°
20.(2020·鄞州)吸烟不仅有害健康而且花钱。如果一位吸烟者每天吸一包38元的香烟,那么他每年花在吸烟上的钱大约要( )元。
A.10000 B.14000 C.18000 D.20000
21.(2022·江北)下面各题中,成反比例关系的是( )
A.路程一定,速度和时间 B.时间一定,路程和速度
C.单价一定,总价和数量 D.数量一定,总价和单价
22.(2022·江北)下面各组三个数中,和0.3不能组成比例的是( )
A.2、3、4 B.1、3、10
C.0.3、0.3、0.3 D.3、3、0.3
23.(2022·江北)下列各数中,最接近9.9亿的是( )
A.10亿 B.994000000 C.984000000 D.9.8亿
24.(2022·江北)下列物品中,厚度最接近1毫米的是( )
A.身份证 B.A4纸 C.一元硬币 D.铅笔盒
25.(2022·江北)如果+3表示向东走3米,那么﹣3表示向( )走3米。
A.东 B.南 C.西 D.北
26.(2022·镇海)古希腊的数学家毕达哥拉斯在没有纸笔的时代,用沙子在沙滩上画呀画,发现了数与形的规律。照下面的图形排列规律,第12组图形里共有( )个正方形的顶点。
A.48 B.37 C.24 D.36
27.(2022·镇海)如图,把一个圆沿半径分成若干等分后,拼成一个近似的长方形,近似长方形的周长比圆的周长增加了20厘米,这个圆的面积是( )平方厘米。
A.400π B.100π C.25π D.20π
28.(2022·镇海)学完平行四边形和三角形的面积计算方法后,几位同学尝试解决梯形面积的问题,想法有以下几种。三位同学的想法中,( )
甲: (上底+下底)×高÷2=梯形面积 乙: 4÷2=2(cm)(3+5)×2=16(cm2) 丙: 3×4÷2=6(cm2) 5×4÷2=10(cm2) 6+10=16(cm2)
A.甲对 B.乙对 C.丙对 D.三人都对
29.(2022·镇海)笔算乘法和口算乘法都是先分后合的过程,下面的算式( )可以用如图表示。
8×3 8×10
20×3 20×10
A.23×18 B.23×81 C.13×28 D.38×12
30.(2022·镇海)一瓶水重千克,先倒出它的,再往瓶里加千克。现在瓶里的水比原来( )
A.多 B.少 C.不变 D.无法判断
31.(2022·镇海)某公司的员工平均工资为6000元,王阿姨是该公司的员工,她的工资( )
A.少于6000元 B.多于6000元 C.等于6000元 D.都有可能
32.(2022·黄岩)下列关于正比例和反比例关系的四个说法中,错误的有( )个。
⑴三角形的底一定,它的高和面积成正比例关系。
⑵圆的直径一定,周长和圆周率成正比例关系。
⑶加工零件的总时间一定,每个零件所用的时间和加工零件的个数成反比例。
⑷铺地面积一定,地砖的面积和块数成反比例关系。
A.1 B.2 C.3 D.4
33.(2022·黄岩)如图,有一张方格纸,每个方格的边长是1cm,上面堆叠着棱长为1cm的小正方体,小正方体A的位置用(1,1,1)表示,小正方体B的位置用(7,4,3)表示,则小正方体C的位置用( )示。
A.(3,9,9) B.(9,3,5) C.(3,9,5) D.(9,3,9)
34.(2022·黄岩)如果一个漏水的水龙头每小时漏水2.8千克,估计一下,下面( )的数据最接近这个水龙头一年漏水的质量。
A.24t B.2500kg C.2.5t D.1.1t
35.(2022·黄岩)六年级有200名学生,他们分别订阅了甲、乙、丙、丁四种杂志的一种、两种、三种、四种。至少有( )名学生订阅的杂志种类相同。
A.14 B.18 C.25 D.50
36.(2022·黄岩)某地去年粮食产量2.4万t,比前年增产二成,下面算式表示前年的粮食产量的是( )
A.2.4+2.4×20% B.2.4×(1+20%)
C.2.4÷(1﹣20%) D.2.4÷(1+20%)
37.(2022·黄岩)在一杯含糖率15%的糖水中拌入5克糖和15克水,这时糖水的含糖率( )
A.>15% B.=15% C.<15% D.无法确定
38.(2022·黄岩)走同一条路,小刚用了小时,小明用了小时,则小明与小刚的平均速度之比是( )
A.5:6 B.6:5 C.: D.:
39.(2022·黄岩)下列说法正确的是( )
①正方形有4条对称轴,长方形和平行四边形都有两条对称轴
②五年期存款的年利率是2.75%,2.75%是指一年的利息是本金的
③同时抛掷两枚硬币,两枚都是正面朝上的可能性是
④在比例里,两内项之积与两外项之积的差是0
A.①② B.②④ C.②③ D.③④
40.(2022·黄岩)一个三角形三个内角的度数比是2:3:5,这个三角形是( )三角形。
A.锐角 B.直角 C.钝角 D.都有可能
41.(2022·黄岩)下面各数中,最接近0的是( )
A.﹣ B. C.0.2 D.﹣
42.(2022·黄岩)下面( )大约1公顷。
A.黄岩区的陆地面积 B.永宁公园的面积
C.一个篮球场的占地面积 D.一个操场的占地面积
43.(2022·黄岩)今年(2022年)的第一季度有( )天。
A.88 B.89 C.90 D.91
44.(2022·慈溪)下图是玲玲用小棒和纽扣摆的图案。照这样摆下去,摆n根小棒共需要( )颗纽扣。
A.n B.6n C.2n+4 D.4n+2
45.(2022·慈溪)四个杯子中均装有一定量的开水,如果把50克糖融于水中,含糖率最高的是( )。
A. B.
C. D.
46.(2022·慈溪)某停车场的收费标准如图所示。一辆汽车付停车费34元,那么它的停车时间可能是( )。
A.8∶20~12∶00 B.8∶35~14∶00
C.12∶10~15∶20 D.7∶55~12∶05
47.(2022·慈溪)一辆汽车轮胎表面的一部分刚被涂了油漆。下图表示当车移动时这个轮胎所形成的印迹。那么这个轮胎的周长是( )厘米。
A.158 B.308 C.316 D.466
48.(2022·慈溪)工厂仓库里有一堆存放货物的正方体纸箱,从上面看到的形状是 ,上面的数字表示在这个位置上所用正方体纸箱的个数。这堆纸箱从正面看是( )。
A. B.
C. D.
49.(2022·慈溪)下图是一个空酒瓶,如果匀速地往里面注酒,下面大约能表示酒面上升速度的图象是( )。
A. B.
C. D.
50.(2022·慈溪)一种精密零件长5毫米,把它画在图纸上,量得零件长6厘米,这张图纸的比例尺是( )。
A.5∶6 B.6∶5 C.12∶1 D.1∶12
答案解析部分
1.B
解:甲店:(2×5)×(1﹣16%),
=10×84%,
=8.4(元);
乙店:2×4=8(元);
丙店:(2×5)×90%,
=10×90%,
=9(元);
8<8.4<9.
所以乙店最便宜.
故选:B.
甲店:降价16%,是把原价看成单位“1”,现价是原价的(1﹣16%),由此求出5袋的现价;
乙店:买四赠一,买五袋牛奶只需要付4袋的钱即可,由此求出5袋的现价;
丙店:打九折是指现价是原价的90%,把原价看成单位“1”,由此求出5袋的现价.
2.C
解:丁丁的订餐号:0291。
故答案为:C。
最小的是自然数是1;最小的质数是2;一位数中既是奇数又是合数的数是9;自然数的计数单位是1。
3.C
解:选项A,2008÷4=502,所以2008年是闰年,神舟七号载人飞船是2008年成功发射,即不符合题意;
选项B,2016÷4=504,所以2016年是闰年,2016年中国女排重夺奥运冠军,说法正确,即不符合题意;
选项C,2010÷4=502……2,所以2010年是平年,即上海世博会举办不是发生在闰年,说法错误,即符合题意;
选项D,2020÷4=505,所以2020年是闰年,2020年我国再次完成珠峰测高任务,说法正确,即不符合题意。
故答案为:C。
平年、闰年的判断方法:①普通年能被4整除且不能被100整除的为闰年。(如2004年就是闰年,1900年不是闰年);②世纪年能被400整除的是闰年。(如2000年是闰年,1900年不是闰年)。
4.C
解:假设乙仓库的存货量为1,则甲仓库的存货量为:
1×(1+20%)=120%;
丙仓库的存货量为:
1÷(1-20%)
=1÷80%
=1.25
1.25>120%>1,丙仓库的存货量最多,乙仓库的存货量最少。
故答案为:C。
假设乙仓库的存货量为1,则甲仓库的存货量1×(1+多的百分率)=120%;丙仓库的存货量为1÷(1-少的百分率)=1.25,然后比较大小。
5.C
解:2020÷4=505,2020年是闰年,2月29天;
31+29+31
=60+31
=91(天)。
故答案为:C。
平年和闰年的判断方法:公历年份是4的倍数的是闰年,但公历年份是整百的必须是400的倍数的才是闰年;平年的二月28天,闰年2月29天,2020年的1月份、2月份、3月份一共的天数=三个月的天数相加。
6.A
解:(80×20)÷(20-4)-80
=1600÷16-80
=100-80
=20(米)。
故答案为:A。
每天要比计划多修的米数=(计划平均每天修的米数×计划修的天数)÷(计划修的天数-提前的天数)-计划平均每天修的米数。
7.B
解:(501-240)×x=261x(元)。
故答案为:B。
王老师家七月应该缴纳电费金额=(八月电表读数-七月电表读数) ×家用电的单价。
8.B
解:1÷-1
=5-1
=4(次)。
故答案为:B。
要截的次数=截的段数-1,其中,截的段数=铁丝的总长÷平均每小段的长度。
9.C
解:A:比5大的数字有4个,比5小的数字有5个,抽到比5大的数字的可能性比较小,说法错误;
B:提价和降价的比较量不同,价格会改变,原题说法错误;
C:表示一周内气温的变化情况,选用折线统计图比较合适,说法正确;
D:2是偶数不是合数,原题说法错误。
故答案为:C。
A:在总数中占的数量多,摸到的可能性就大,占的数量小,摸到的可能性就小;
B:原价×(1+20%)×(1-20%)=现价,据此解答。
C:折线统计图不但可以表示出数据的多少,还可以描述出其变化趋势;
D:除2以外,所有的偶数都是合数。
10.C
解:面积计算方法的思路和对应的算式错误的是第三个。
故答案为:C。
C中,平行四边形的面积是ah,不用在除以2,据此解答。
11.B
解:算式中箭头所指的3在十位上,表示30,指的是3×10,表示②区域的意思。
故答案为:B。
②区域的长是3,宽是10,面积是30。
12.D
解:解法不正确是1800×(1+)。
故答案为:D。
短袖衬衫数÷对应的长袖衬衫数的百分率=长袖衬衫数,短袖衬衫数+长袖衬衫数=短袖和长袖衬衫一共的件数,所以A正确;
短袖衬衫数:对应的份数=短袖和长袖衬衫一共的件数:对应的份数,所以B正确;
短袖衬衫数÷对应的份数=1份的量,1份的量×7份=短袖和长袖衬衫一共的件数,所以C正确。
13.B
解:从前面看到的图形是第二个图形。
故答案为:B。
从前面看到三竖列,第一竖列有1个小正方形,第二竖列有3个小正方形,第三竖列有1个小正方形。
14.C
解:105500平方千米×=10550(平方千米)
10000平方千米比较接近
故答案为:C。
宁波市的面积大约是浙江省的左右,浙江省的占地面积×=宁波市的面积。
15.D
解:题干中的方法称为割圆术。
故答案为:D。
割圆术的特点概括为割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣。刘徽这种想法的可贵之处在于用已知的、可求的来逼近未知的、要求的,用有限来逼近无限。这种思想极其重要,对后世产生了巨大影响。
16.B
解:应该向东北方向走。
故答案为:B。
找一个地方在另一个地方什么位置,就以另一个地方为观测点,根据方向、角度、距离确定物体的位置。
17.A
解:A:0.80 中的8在十分位上,表示8个0.1;
B:中的8在百分位上,表示8个0.01;
C:8% 中的8在百分位上,表示8个0.01;
D:0.08 中的8在百分位上,表示8个0.01。
故答案为:A。
一个数字在哪个数位上,就表示有几个这个数位上的数。
18.B
解:S=0,
NSNSNS能被5整除,
N+N+N的和一定是3的倍数,
NSNSNS也一定能被3整除,
故选B.
NSNSNS个位上的数字是0,能被5整除,不管N是比10小的哪个自然数,N+N+N的和一定是3的倍数,所以NSNSNS也一定能被3整除,所以选B.
19.A
解:60°,60°,60°是等边三角形,所以对称轴最多。
故答案为:A。
三角形中,等腰三角形有1条对称轴,等边三角形的对称轴条数最多,有3条。
20.B
解:38×365
≈40×350
=14000(元)
所以每年花在吸烟上的钱大约要14000元。
故答案为:B。
一年花费的总钱数=每天吸一包烟的钱数×一年的天数,接下来将两个因数看成与它接近的整十数进行相乘,即可得出他每年花在吸烟上的钱大约要用的钱数。
21.A
解:选项A:路程一定,速度和时间成反比例关系;
选项B:时间一定,路程和速度成正比例关系;
选项C:单价一定,总价和数量成正比例关系;
选项D:数量一定,总价和单价成正比例关系。
故答案为:A。
正比例:两种相关联的量,一种量变化,另一种量也随之变化,如果这两种量中相对应的的比值一定,这两种量就叫做成正比例的量,它们的关系就叫做正比例关系。
反比例:两种相关联的量,一种量变化,另一种量也随之变化,如果这两种量中相对应的的乘积一定,这两种量就叫做成反比例的量,它们的关系就叫做反比例关系。
22.A
解:选项A:2、3、4和0.3不可以组成比例;
选项B:1:10=0.3:3,可以组成比例;
选项C:0.3:0.3=0.3:0.3,可以组成比例;
选项D:0.3:0.3=3:3,可以组成比例。
故答案为:A。
比值相等的两个比可以组成比例。
23.B
解:选项A:10亿-9.9亿=0.1亿;
选项B:9.9亿-994000000=0.04亿;
选项C:9.9亿-984000000=0.06亿;
选项D:9.9亿-9.8亿=0.1亿;
0.04亿<0.06亿<0.1亿。
故答案为:B。
计算出每个选项中的数与9.9亿的差,差最小的数与9.9亿最接近。
24.A
解:选项A:身份证的厚度大约是1毫米,原题干说法正确;
选项B:A4纸的厚度大约是0.1毫米,原题干说法错误;
选项C:一元硬币的厚度大约是2毫米,原题干说法错误;
选项D:铅笔盒的厚度大约是50毫米,原题干说法错误。
故答案为:A。
根据实际情况和数据大小选择合适的计量单位。
25.C
解:如果+3表示向东走3米,那么﹣3表示向西走3米。
故答案为:C。
正数和负数表示意义相反的两种量。
26.B
解:3×12+1
=36+1
=37(个)。
故答案为:B。
第n组图形里共有正方形顶点的个数=(3n+1) 个。
27.B
解:20÷2=10(厘米)
π×102=100π。
故答案为:B。
这个圆的面积=π×半径2;其中,半径= 增加的周长÷2。
28.D
解:三位同学的想法都对。
故答案为:D。
在推导梯形的面积计算公式时,①可以用两个完全一样的梯形拼成一个平行四边形,进而推导出梯形的面积=(上底+下底)×高÷2;②用割补法,把梯形拼成平行四边形;③用割补法,把梯形拼成三角形,进而求出梯形的面积。
29.C
解:13×28=8×3+8×10+20×3+20×10。
故答案为:C。
两位数乘两位数的笔算乘法,相同数位对齐,先用第二个因数个位上的数去乘第一个因数,再用十位上去乘第一个因数,最后把两次乘得的积相加。
30.A
解:×=(千克)
<千克,则现在瓶里的水比原来多。
故答案为:A。
倒出水的质量=一瓶水的总质量×倒出的分率,然后和往瓶子里再加水的质量比较大小。
31.D
解:王阿姨可能大于、小于或者等于6000元。
故答案为:D。
平均数表示一组数据的平均水平,某公司的员工平均工资为6000元,王阿姨是该公司的员工,她的工资可能大于、小于或者等于6000元。
32.A
解:(1)面积×2÷高=三角形的底(一定),三角形的底一定,它的高和面积成正比例关系,原题干说法正确;
(2)圆周率π是一个定值,圆的直径一定,周长和圆周率不成比例,原题干说法错误;
(3)平均每个零件所用的时间×加工零件的个数=加工零件的总时间(一定),加工零件的总时间一定,每个零件所用的时间和加工零件的个数成反比例,原题干说法正确;
(4)地砖的面积×块数=铺地面积(一定),铺地面积一定,地砖的面积和块数成反比例关系,原题干说法正确。
故答案为:A。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量;两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量。
33.C
解:小正方体C的位置用(3,9,5)示。
故答案为:C。
小正方体C的位置在第3列,第9行,小正方体有5个,用(3,9,5)示。
34.A
解:2.8×24×365
=67.2×365
=24528(千克),24528千克大约24吨。
故答案为:A。
这个水龙头一年漏水的质量=平均每小时漏水的质量×每天24小时×每年的天数。
35.A
解:4+6+4+1=15(种)
200÷15=13(名)······5(名)
13+1=14(名)。
故答案为:A。
订阅杂志中的一种有4种选法, 订阅杂志中的两种有6种选法,订阅杂志中的三种有4种选法,订阅杂志中的一种有1种选法,共有4+6+4+1=15种,把15种看作15个抽屉,把订阅杂志的人数(200人)看元素,至少在同一抽屉里相同物体的个数=物体总个数÷抽屉的个数+1。
36.D
解:表示前年的粮食产量的是:2.4÷(1+20%)。
故答案为:D。
前年粮食的产量=去年粮食的产量÷(1+增产的成数)。
37.A
解:5÷(5+15)
=5÷20
=25%
15%<25%,这时糖水的含糖率>15%。
故答案为:A。
含糖率=糖的质量÷(糖的质量+水的质量),原来的含糖率是15%,现在拌入糖水的含糖率是25%,所以这时糖水的含糖率>15%。
38.A
解:(1÷):(1÷)=:3=5:6.
故答案为:A。
速度=路程÷时间,写出比后依据比的基本性质化简比。
39.B
解:①正方形有4条对称轴,长方形有两条对称轴,平行四边形没有对称轴,原题干说法错误;
②五年期存款的年利率是2.75%,2.75%是指一年的利息是本金的,原题干说法正确;
③1÷4=,原题干说法错误;
④在比例里,两内项之积与两外项之积的差是0,原题干说法正确。
故答案为:B。
①依据轴对称图形的定义判断:平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这个图形就是轴对称图形;其中的这条直线就是对称轴;
②五年期存款的年利率是2.75%,2.75%是指一年的利息是本金的;
③同时抛掷两枚硬币,出现的结果又:两正、两反、一正一反、一反一正,两枚都是正面朝上的可能性是1÷4=;
④比例的基本性质:在比例里,两个内项积等于两个外项积,所以两内项之积与两外项之积的差是0。
40.B
解:180÷(2+3+5)×5
=180÷10×5
=18×5
=90(度),这个三角形是直角三角形。
故答案为:B。
三角形中最大内角的度数=三角形的内角和÷总份数×最大内角占的份数。
41.C
解:-≈-3.33;
=1÷4=0.25;
-=-0.5,最接近0的是0.2。
故答案为:C。
分数化成小数,用分数的分子除以分母,然后比较大小。
42.B
解:永宁公园的面积大约1公顷。
故答案为:B。
根据实际生活经验以及题干中的具体数据来选择。
43.C
解:2022÷4=505······2,2022年是平年;2月28天;
31+28+31
=59+31
=90(天)。
故答案为:C。
今年(2022年)的第一季度的天数=1月的天数+2月的天数+3月的天数;其中,2022年是平年;2月28天。
44.D
解:摆n根小棒共需要4n+2颗纽扣。
故答案为:D。
摆1根小棒共需要纽扣的颗数:6=4×1+2;
摆2根小棒共需要纽扣的颗数:10=4×2+2;
摆1根小棒共需要纽扣的颗数:14=4×3+2;
……
摆n根小棒共需要纽扣的颗数:4n+2。
45.A
解:A项中,(6÷2)2×3.14×6×=56.52(立方厘米);
B项中,4×4×6=96(立方厘米);
C项中,6×6×6=216(立方厘米);
D项中,(4÷2)2×3.14×6=75.36(立方厘米)。
56.52<75.36<96<216,所以含糖率最高的是A项中的杯子。
故答案为:A。
圆锥的体积=πr2h×;长方体的体积=长×宽×高;正方体的体积=棱长×棱长×棱长;圆柱的体积=πr2h。
因为糖的质量相同,所以水的体积越大,含糖率越低。
46.D
解:34-10=24元,24÷8=3小时,2+3=5小时,所以这辆汽车的停车时间超过4小时不超过5小时。
A项中,12时-8时20分=3小时40分钟<4小时,所以不合适;
B项中,14时-8时35分=5小时25分钟>5小时,所以不合适;
C项中,15时20分-12时10分=3小时10分钟<4小时,所以不合适;
D项中,12时5分-7时55分=4小时10分钟,所以合适。
故答案为:D。
超出2小时收的钱数=付的钱数-2小时以内的收费,所以超出2小时再经过的时间=超出2小时收的钱数÷超出2小时经过的时间,由此可以得出停车的时间,然后根据选项经过的时间作答即可。
47.B
解:616÷2=308厘米,所以这个轮胎的周长是308厘米。
故答案为:B。
从印记可以得到,616cm表示车轮滚了2周,所以这个轮胎的周长=车轮滚动2周走的距离÷2。
48.A
解:这堆纸箱从正面看是A项中的图形。
故答案为:A。
由题意可知,这堆纸箱从正面看是三列正方形,最左边一列是2个正方形,中间一列是3个正方形,最右边是1个正方形。
49.B
解:B项中的图像能表示酒面上升速度。
故答案为:B。
从图中可以看出,瓶子上面的部分比下面细,所以图像的斜率会增大。
50.C
解:6厘米=60毫米,60:5=12:1,所以这张图纸的比例尺是12:1。
故答案为:C。
先把单位进行换算,即1厘米=10毫米,那么比例尺=图上距离:实际距离。
2025年浙江省小升初数学近三年真题分类汇编
专题05 选择题50题
一、单选题
1.(2024·浙江)原价每袋2元的某种牛奶,甲、乙、丙三店均在搞促销活动,甲商店每袋降价16%,乙商店“买四送一”,丙商店每袋打9折出售,小明要买5袋牛奶,应从( )商店购买比较便宜.
A.甲 B.乙 C.丙 D.三店均可
2.(2023·海曙)丁丁在肯德基订餐,他的订餐号是一个四位数,左起第一位是最小的自然数,第二位是最小的质数,第三位既是奇数又是合数,第四位是自然数的计数单位,他的订餐号是( )
A.1920 B.1390 C.0291 D.0231
3.(2023两江巴蜀)不是发生在闰年的大事是( )。
A.2008年神舟七号载人飞船成功发射
B.2016年中国女排重夺奥运冠军
C.2010年上海世博会举办
D.2020年我国再次完成珠峰测高任务
4.(2023·柯城)甲仓货存量比乙仓多20%,乙仓货存量比丙仓少20%,那么货存量( )
A.甲仓最多 B.乙仓最多 C.丙仓最多 D.无法判断
5.(2023·柯城)2020年的1月份、2月份、3月份一共有( )天。
A.89 B.90 C.91 D.92
6.(2023·柯城)修一条水渠,计划每天修80m,20天可以完成,如果要提前4天完成,那么每天要比计划多修( )米。
A.20 B.60 C.64 D.100
7.(2023·柯城)王老师家的电表七月抄表数是240度,八月抄表数是501度,已知家用电的价格是每度x元,那么王老师家七月应该缴纳电费( )元。
A.501x B.261x C.240x D.741x
8.(2023·柯城)把1米长的铁丝截成每段长米的小段,要截( )次。
A.3 B.4 C.5 D.6
9.(2023六下·海曙)下列说法正确的是( )。
A.从0~9这10张数字卡片中,任意抽取1张,抽到比5大的数字的可能性比较大
B.一个笔盒提价20%后又降价20%,价格不变。
C.表示一周内气温的变化情况,选用折线统计图比较合适。
D.所有的偶数都是合数。
10.(2023六下·海曙)在研究梯形的面积公式时,下列面积计算方法的思路和对应的算式错误的是( )。
A.(a+b)h÷2
B.ah÷2+bh÷2
C.ah÷2+(b-a)h÷2
D.(a+b)+bh÷2
11.(2023六下·海曙)下面是乐乐计算23×12的思路,他用①、②、③、④四个区域来表示计算过程。算式中“←”所指向的“3”表示( )区域的意思。
A.① B.② C.③ D.④
12.(2023六下·海曙)仓库里有短袖衬衫1800件,是长袖衬衫数的75%,短袖和长袖衬衫一共多少件?下面解法中,不正确是( )。
A.1800÷75%+1800 B.1800∶3=x∶(3+4)
C.1800÷3×(3+4) D.1800×(1+)
13.(2023六下·海曙)王芳用小正方体积木搭成的图形,从上面看到的图形如下图(积木上的数字表示这个位置上所用的小正方体的个数),从前面看到的图形是( )。
A. B.
C. D.
14.(2023六下·海曙)浙江省的占地面积约105500平方千米,宁波市的面积大约是( )平方千米。
A.50000 B.20000 C.10000 D.5000
15.(2023六下·海曙)魏晋时期的数学家刘徽从圆内接正六边形开始,将边数逐次加倍,得到的圆内接正多边形就逐步逼近圆,为此来计算圆的周长、面积以及圆周率。这种方法称为( )。
A.刘徽法 B.近圆术 C.圆中方 D.割圆术
16.(2023六下·海曙)象棋规则口诀中有“马走日”、“象走田”的说法。在下面的棋局中,如果用“象”吃掉对方的“兵”,应该向( )方向走。
A.西北 B.东北 C.西南 D.东南
17.(2023六下·海曙)下面各数中“8”表示的意义不同的是( )。
A.0.80 B. C.8% D.0.08
18.(2023·宁波)下面四个数都是六位数,N是比10小的自然数,S是0,一定能被3和5整除的数是( )
A.NNNSNN B.NSNSNS C.NSSNSS D.NSSNSN
19.(2020·慈溪)根据三角形三个角的度数,判断下面三角形中对称轴最多的是( )
A.60°,60°,60° B.90°,45°,45°
C.90°,60°,30° D.120°,40°,20°
20.(2020·鄞州)吸烟不仅有害健康而且花钱。如果一位吸烟者每天吸一包38元的香烟,那么他每年花在吸烟上的钱大约要( )元。
A.10000 B.14000 C.18000 D.20000
21.(2022·江北)下面各题中,成反比例关系的是( )
A.路程一定,速度和时间 B.时间一定,路程和速度
C.单价一定,总价和数量 D.数量一定,总价和单价
22.(2022·江北)下面各组三个数中,和0.3不能组成比例的是( )
A.2、3、4 B.1、3、10
C.0.3、0.3、0.3 D.3、3、0.3
23.(2022·江北)下列各数中,最接近9.9亿的是( )
A.10亿 B.994000000 C.984000000 D.9.8亿
24.(2022·江北)下列物品中,厚度最接近1毫米的是( )
A.身份证 B.A4纸 C.一元硬币 D.铅笔盒
25.(2022·江北)如果+3表示向东走3米,那么﹣3表示向( )走3米。
A.东 B.南 C.西 D.北
26.(2022·镇海)古希腊的数学家毕达哥拉斯在没有纸笔的时代,用沙子在沙滩上画呀画,发现了数与形的规律。照下面的图形排列规律,第12组图形里共有( )个正方形的顶点。
A.48 B.37 C.24 D.36
27.(2022·镇海)如图,把一个圆沿半径分成若干等分后,拼成一个近似的长方形,近似长方形的周长比圆的周长增加了20厘米,这个圆的面积是( )平方厘米。
A.400π B.100π C.25π D.20π
28.(2022·镇海)学完平行四边形和三角形的面积计算方法后,几位同学尝试解决梯形面积的问题,想法有以下几种。三位同学的想法中,( )
甲: (上底+下底)×高÷2=梯形面积 乙: 4÷2=2(cm)(3+5)×2=16(cm2) 丙: 3×4÷2=6(cm2) 5×4÷2=10(cm2) 6+10=16(cm2)
A.甲对 B.乙对 C.丙对 D.三人都对
29.(2022·镇海)笔算乘法和口算乘法都是先分后合的过程,下面的算式( )可以用如图表示。
8×3 8×10
20×3 20×10
A.23×18 B.23×81 C.13×28 D.38×12
30.(2022·镇海)一瓶水重千克,先倒出它的,再往瓶里加千克。现在瓶里的水比原来( )
A.多 B.少 C.不变 D.无法判断
31.(2022·镇海)某公司的员工平均工资为6000元,王阿姨是该公司的员工,她的工资( )
A.少于6000元 B.多于6000元 C.等于6000元 D.都有可能
32.(2022·黄岩)下列关于正比例和反比例关系的四个说法中,错误的有( )个。
⑴三角形的底一定,它的高和面积成正比例关系。
⑵圆的直径一定,周长和圆周率成正比例关系。
⑶加工零件的总时间一定,每个零件所用的时间和加工零件的个数成反比例。
⑷铺地面积一定,地砖的面积和块数成反比例关系。
A.1 B.2 C.3 D.4
33.(2022·黄岩)如图,有一张方格纸,每个方格的边长是1cm,上面堆叠着棱长为1cm的小正方体,小正方体A的位置用(1,1,1)表示,小正方体B的位置用(7,4,3)表示,则小正方体C的位置用( )示。
A.(3,9,9) B.(9,3,5) C.(3,9,5) D.(9,3,9)
34.(2022·黄岩)如果一个漏水的水龙头每小时漏水2.8千克,估计一下,下面( )的数据最接近这个水龙头一年漏水的质量。
A.24t B.2500kg C.2.5t D.1.1t
35.(2022·黄岩)六年级有200名学生,他们分别订阅了甲、乙、丙、丁四种杂志的一种、两种、三种、四种。至少有( )名学生订阅的杂志种类相同。
A.14 B.18 C.25 D.50
36.(2022·黄岩)某地去年粮食产量2.4万t,比前年增产二成,下面算式表示前年的粮食产量的是( )
A.2.4+2.4×20% B.2.4×(1+20%)
C.2.4÷(1﹣20%) D.2.4÷(1+20%)
37.(2022·黄岩)在一杯含糖率15%的糖水中拌入5克糖和15克水,这时糖水的含糖率( )
A.>15% B.=15% C.<15% D.无法确定
38.(2022·黄岩)走同一条路,小刚用了小时,小明用了小时,则小明与小刚的平均速度之比是( )
A.5:6 B.6:5 C.: D.:
39.(2022·黄岩)下列说法正确的是( )
①正方形有4条对称轴,长方形和平行四边形都有两条对称轴
②五年期存款的年利率是2.75%,2.75%是指一年的利息是本金的
③同时抛掷两枚硬币,两枚都是正面朝上的可能性是
④在比例里,两内项之积与两外项之积的差是0
A.①② B.②④ C.②③ D.③④
40.(2022·黄岩)一个三角形三个内角的度数比是2:3:5,这个三角形是( )三角形。
A.锐角 B.直角 C.钝角 D.都有可能
41.(2022·黄岩)下面各数中,最接近0的是( )
A.﹣ B. C.0.2 D.﹣
42.(2022·黄岩)下面( )大约1公顷。
A.黄岩区的陆地面积 B.永宁公园的面积
C.一个篮球场的占地面积 D.一个操场的占地面积
43.(2022·黄岩)今年(2022年)的第一季度有( )天。
A.88 B.89 C.90 D.91
44.(2022·慈溪)下图是玲玲用小棒和纽扣摆的图案。照这样摆下去,摆n根小棒共需要( )颗纽扣。
A.n B.6n C.2n+4 D.4n+2
45.(2022·慈溪)四个杯子中均装有一定量的开水,如果把50克糖融于水中,含糖率最高的是( )。
A. B.
C. D.
46.(2022·慈溪)某停车场的收费标准如图所示。一辆汽车付停车费34元,那么它的停车时间可能是( )。
A.8∶20~12∶00 B.8∶35~14∶00
C.12∶10~15∶20 D.7∶55~12∶05
47.(2022·慈溪)一辆汽车轮胎表面的一部分刚被涂了油漆。下图表示当车移动时这个轮胎所形成的印迹。那么这个轮胎的周长是( )厘米。
A.158 B.308 C.316 D.466
48.(2022·慈溪)工厂仓库里有一堆存放货物的正方体纸箱,从上面看到的形状是 ,上面的数字表示在这个位置上所用正方体纸箱的个数。这堆纸箱从正面看是( )。
A. B.
C. D.
49.(2022·慈溪)下图是一个空酒瓶,如果匀速地往里面注酒,下面大约能表示酒面上升速度的图象是( )。
A. B.
C. D.
50.(2022·慈溪)一种精密零件长5毫米,把它画在图纸上,量得零件长6厘米,这张图纸的比例尺是( )。
A.5∶6 B.6∶5 C.12∶1 D.1∶12
答案解析部分
1.B
解:甲店:(2×5)×(1﹣16%),
=10×84%,
=8.4(元);
乙店:2×4=8(元);
丙店:(2×5)×90%,
=10×90%,
=9(元);
8<8.4<9.
所以乙店最便宜.
故选:B.
甲店:降价16%,是把原价看成单位“1”,现价是原价的(1﹣16%),由此求出5袋的现价;
乙店:买四赠一,买五袋牛奶只需要付4袋的钱即可,由此求出5袋的现价;
丙店:打九折是指现价是原价的90%,把原价看成单位“1”,由此求出5袋的现价.
2.C
解:丁丁的订餐号:0291。
故答案为:C。
最小的是自然数是1;最小的质数是2;一位数中既是奇数又是合数的数是9;自然数的计数单位是1。
3.C
解:选项A,2008÷4=502,所以2008年是闰年,神舟七号载人飞船是2008年成功发射,即不符合题意;
选项B,2016÷4=504,所以2016年是闰年,2016年中国女排重夺奥运冠军,说法正确,即不符合题意;
选项C,2010÷4=502……2,所以2010年是平年,即上海世博会举办不是发生在闰年,说法错误,即符合题意;
选项D,2020÷4=505,所以2020年是闰年,2020年我国再次完成珠峰测高任务,说法正确,即不符合题意。
故答案为:C。
平年、闰年的判断方法:①普通年能被4整除且不能被100整除的为闰年。(如2004年就是闰年,1900年不是闰年);②世纪年能被400整除的是闰年。(如2000年是闰年,1900年不是闰年)。
4.C
解:假设乙仓库的存货量为1,则甲仓库的存货量为:
1×(1+20%)=120%;
丙仓库的存货量为:
1÷(1-20%)
=1÷80%
=1.25
1.25>120%>1,丙仓库的存货量最多,乙仓库的存货量最少。
故答案为:C。
假设乙仓库的存货量为1,则甲仓库的存货量1×(1+多的百分率)=120%;丙仓库的存货量为1÷(1-少的百分率)=1.25,然后比较大小。
5.C
解:2020÷4=505,2020年是闰年,2月29天;
31+29+31
=60+31
=91(天)。
故答案为:C。
平年和闰年的判断方法:公历年份是4的倍数的是闰年,但公历年份是整百的必须是400的倍数的才是闰年;平年的二月28天,闰年2月29天,2020年的1月份、2月份、3月份一共的天数=三个月的天数相加。
6.A
解:(80×20)÷(20-4)-80
=1600÷16-80
=100-80
=20(米)。
故答案为:A。
每天要比计划多修的米数=(计划平均每天修的米数×计划修的天数)÷(计划修的天数-提前的天数)-计划平均每天修的米数。
7.B
解:(501-240)×x=261x(元)。
故答案为:B。
王老师家七月应该缴纳电费金额=(八月电表读数-七月电表读数) ×家用电的单价。
8.B
解:1÷-1
=5-1
=4(次)。
故答案为:B。
要截的次数=截的段数-1,其中,截的段数=铁丝的总长÷平均每小段的长度。
9.C
解:A:比5大的数字有4个,比5小的数字有5个,抽到比5大的数字的可能性比较小,说法错误;
B:提价和降价的比较量不同,价格会改变,原题说法错误;
C:表示一周内气温的变化情况,选用折线统计图比较合适,说法正确;
D:2是偶数不是合数,原题说法错误。
故答案为:C。
A:在总数中占的数量多,摸到的可能性就大,占的数量小,摸到的可能性就小;
B:原价×(1+20%)×(1-20%)=现价,据此解答。
C:折线统计图不但可以表示出数据的多少,还可以描述出其变化趋势;
D:除2以外,所有的偶数都是合数。
10.C
解:面积计算方法的思路和对应的算式错误的是第三个。
故答案为:C。
C中,平行四边形的面积是ah,不用在除以2,据此解答。
11.B
解:算式中箭头所指的3在十位上,表示30,指的是3×10,表示②区域的意思。
故答案为:B。
②区域的长是3,宽是10,面积是30。
12.D
解:解法不正确是1800×(1+)。
故答案为:D。
短袖衬衫数÷对应的长袖衬衫数的百分率=长袖衬衫数,短袖衬衫数+长袖衬衫数=短袖和长袖衬衫一共的件数,所以A正确;
短袖衬衫数:对应的份数=短袖和长袖衬衫一共的件数:对应的份数,所以B正确;
短袖衬衫数÷对应的份数=1份的量,1份的量×7份=短袖和长袖衬衫一共的件数,所以C正确。
13.B
解:从前面看到的图形是第二个图形。
故答案为:B。
从前面看到三竖列,第一竖列有1个小正方形,第二竖列有3个小正方形,第三竖列有1个小正方形。
14.C
解:105500平方千米×=10550(平方千米)
10000平方千米比较接近
故答案为:C。
宁波市的面积大约是浙江省的左右,浙江省的占地面积×=宁波市的面积。
15.D
解:题干中的方法称为割圆术。
故答案为:D。
割圆术的特点概括为割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣。刘徽这种想法的可贵之处在于用已知的、可求的来逼近未知的、要求的,用有限来逼近无限。这种思想极其重要,对后世产生了巨大影响。
16.B
解:应该向东北方向走。
故答案为:B。
找一个地方在另一个地方什么位置,就以另一个地方为观测点,根据方向、角度、距离确定物体的位置。
17.A
解:A:0.80 中的8在十分位上,表示8个0.1;
B:中的8在百分位上,表示8个0.01;
C:8% 中的8在百分位上,表示8个0.01;
D:0.08 中的8在百分位上,表示8个0.01。
故答案为:A。
一个数字在哪个数位上,就表示有几个这个数位上的数。
18.B
解:S=0,
NSNSNS能被5整除,
N+N+N的和一定是3的倍数,
NSNSNS也一定能被3整除,
故选B.
NSNSNS个位上的数字是0,能被5整除,不管N是比10小的哪个自然数,N+N+N的和一定是3的倍数,所以NSNSNS也一定能被3整除,所以选B.
19.A
解:60°,60°,60°是等边三角形,所以对称轴最多。
故答案为:A。
三角形中,等腰三角形有1条对称轴,等边三角形的对称轴条数最多,有3条。
20.B
解:38×365
≈40×350
=14000(元)
所以每年花在吸烟上的钱大约要14000元。
故答案为:B。
一年花费的总钱数=每天吸一包烟的钱数×一年的天数,接下来将两个因数看成与它接近的整十数进行相乘,即可得出他每年花在吸烟上的钱大约要用的钱数。
21.A
解:选项A:路程一定,速度和时间成反比例关系;
选项B:时间一定,路程和速度成正比例关系;
选项C:单价一定,总价和数量成正比例关系;
选项D:数量一定,总价和单价成正比例关系。
故答案为:A。
正比例:两种相关联的量,一种量变化,另一种量也随之变化,如果这两种量中相对应的的比值一定,这两种量就叫做成正比例的量,它们的关系就叫做正比例关系。
反比例:两种相关联的量,一种量变化,另一种量也随之变化,如果这两种量中相对应的的乘积一定,这两种量就叫做成反比例的量,它们的关系就叫做反比例关系。
22.A
解:选项A:2、3、4和0.3不可以组成比例;
选项B:1:10=0.3:3,可以组成比例;
选项C:0.3:0.3=0.3:0.3,可以组成比例;
选项D:0.3:0.3=3:3,可以组成比例。
故答案为:A。
比值相等的两个比可以组成比例。
23.B
解:选项A:10亿-9.9亿=0.1亿;
选项B:9.9亿-994000000=0.04亿;
选项C:9.9亿-984000000=0.06亿;
选项D:9.9亿-9.8亿=0.1亿;
0.04亿<0.06亿<0.1亿。
故答案为:B。
计算出每个选项中的数与9.9亿的差,差最小的数与9.9亿最接近。
24.A
解:选项A:身份证的厚度大约是1毫米,原题干说法正确;
选项B:A4纸的厚度大约是0.1毫米,原题干说法错误;
选项C:一元硬币的厚度大约是2毫米,原题干说法错误;
选项D:铅笔盒的厚度大约是50毫米,原题干说法错误。
故答案为:A。
根据实际情况和数据大小选择合适的计量单位。
25.C
解:如果+3表示向东走3米,那么﹣3表示向西走3米。
故答案为:C。
正数和负数表示意义相反的两种量。
26.B
解:3×12+1
=36+1
=37(个)。
故答案为:B。
第n组图形里共有正方形顶点的个数=(3n+1) 个。
27.B
解:20÷2=10(厘米)
π×102=100π。
故答案为:B。
这个圆的面积=π×半径2;其中,半径= 增加的周长÷2。
28.D
解:三位同学的想法都对。
故答案为:D。
在推导梯形的面积计算公式时,①可以用两个完全一样的梯形拼成一个平行四边形,进而推导出梯形的面积=(上底+下底)×高÷2;②用割补法,把梯形拼成平行四边形;③用割补法,把梯形拼成三角形,进而求出梯形的面积。
29.C
解:13×28=8×3+8×10+20×3+20×10。
故答案为:C。
两位数乘两位数的笔算乘法,相同数位对齐,先用第二个因数个位上的数去乘第一个因数,再用十位上去乘第一个因数,最后把两次乘得的积相加。
30.A
解:×=(千克)
<千克,则现在瓶里的水比原来多。
故答案为:A。
倒出水的质量=一瓶水的总质量×倒出的分率,然后和往瓶子里再加水的质量比较大小。
31.D
解:王阿姨可能大于、小于或者等于6000元。
故答案为:D。
平均数表示一组数据的平均水平,某公司的员工平均工资为6000元,王阿姨是该公司的员工,她的工资可能大于、小于或者等于6000元。
32.A
解:(1)面积×2÷高=三角形的底(一定),三角形的底一定,它的高和面积成正比例关系,原题干说法正确;
(2)圆周率π是一个定值,圆的直径一定,周长和圆周率不成比例,原题干说法错误;
(3)平均每个零件所用的时间×加工零件的个数=加工零件的总时间(一定),加工零件的总时间一定,每个零件所用的时间和加工零件的个数成反比例,原题干说法正确;
(4)地砖的面积×块数=铺地面积(一定),铺地面积一定,地砖的面积和块数成反比例关系,原题干说法正确。
故答案为:A。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量;两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量。
33.C
解:小正方体C的位置用(3,9,5)示。
故答案为:C。
小正方体C的位置在第3列,第9行,小正方体有5个,用(3,9,5)示。
34.A
解:2.8×24×365
=67.2×365
=24528(千克),24528千克大约24吨。
故答案为:A。
这个水龙头一年漏水的质量=平均每小时漏水的质量×每天24小时×每年的天数。
35.A
解:4+6+4+1=15(种)
200÷15=13(名)······5(名)
13+1=14(名)。
故答案为:A。
订阅杂志中的一种有4种选法, 订阅杂志中的两种有6种选法,订阅杂志中的三种有4种选法,订阅杂志中的一种有1种选法,共有4+6+4+1=15种,把15种看作15个抽屉,把订阅杂志的人数(200人)看元素,至少在同一抽屉里相同物体的个数=物体总个数÷抽屉的个数+1。
36.D
解:表示前年的粮食产量的是:2.4÷(1+20%)。
故答案为:D。
前年粮食的产量=去年粮食的产量÷(1+增产的成数)。
37.A
解:5÷(5+15)
=5÷20
=25%
15%<25%,这时糖水的含糖率>15%。
故答案为:A。
含糖率=糖的质量÷(糖的质量+水的质量),原来的含糖率是15%,现在拌入糖水的含糖率是25%,所以这时糖水的含糖率>15%。
38.A
解:(1÷):(1÷)=:3=5:6.
故答案为:A。
速度=路程÷时间,写出比后依据比的基本性质化简比。
39.B
解:①正方形有4条对称轴,长方形有两条对称轴,平行四边形没有对称轴,原题干说法错误;
②五年期存款的年利率是2.75%,2.75%是指一年的利息是本金的,原题干说法正确;
③1÷4=,原题干说法错误;
④在比例里,两内项之积与两外项之积的差是0,原题干说法正确。
故答案为:B。
①依据轴对称图形的定义判断:平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这个图形就是轴对称图形;其中的这条直线就是对称轴;
②五年期存款的年利率是2.75%,2.75%是指一年的利息是本金的;
③同时抛掷两枚硬币,出现的结果又:两正、两反、一正一反、一反一正,两枚都是正面朝上的可能性是1÷4=;
④比例的基本性质:在比例里,两个内项积等于两个外项积,所以两内项之积与两外项之积的差是0。
40.B
解:180÷(2+3+5)×5
=180÷10×5
=18×5
=90(度),这个三角形是直角三角形。
故答案为:B。
三角形中最大内角的度数=三角形的内角和÷总份数×最大内角占的份数。
41.C
解:-≈-3.33;
=1÷4=0.25;
-=-0.5,最接近0的是0.2。
故答案为:C。
分数化成小数,用分数的分子除以分母,然后比较大小。
42.B
解:永宁公园的面积大约1公顷。
故答案为:B。
根据实际生活经验以及题干中的具体数据来选择。
43.C
解:2022÷4=505······2,2022年是平年;2月28天;
31+28+31
=59+31
=90(天)。
故答案为:C。
今年(2022年)的第一季度的天数=1月的天数+2月的天数+3月的天数;其中,2022年是平年;2月28天。
44.D
解:摆n根小棒共需要4n+2颗纽扣。
故答案为:D。
摆1根小棒共需要纽扣的颗数:6=4×1+2;
摆2根小棒共需要纽扣的颗数:10=4×2+2;
摆1根小棒共需要纽扣的颗数:14=4×3+2;
……
摆n根小棒共需要纽扣的颗数:4n+2。
45.A
解:A项中,(6÷2)2×3.14×6×=56.52(立方厘米);
B项中,4×4×6=96(立方厘米);
C项中,6×6×6=216(立方厘米);
D项中,(4÷2)2×3.14×6=75.36(立方厘米)。
56.52<75.36<96<216,所以含糖率最高的是A项中的杯子。
故答案为:A。
圆锥的体积=πr2h×;长方体的体积=长×宽×高;正方体的体积=棱长×棱长×棱长;圆柱的体积=πr2h。
因为糖的质量相同,所以水的体积越大,含糖率越低。
46.D
解:34-10=24元,24÷8=3小时,2+3=5小时,所以这辆汽车的停车时间超过4小时不超过5小时。
A项中,12时-8时20分=3小时40分钟<4小时,所以不合适;
B项中,14时-8时35分=5小时25分钟>5小时,所以不合适;
C项中,15时20分-12时10分=3小时10分钟<4小时,所以不合适;
D项中,12时5分-7时55分=4小时10分钟,所以合适。
故答案为:D。
超出2小时收的钱数=付的钱数-2小时以内的收费,所以超出2小时再经过的时间=超出2小时收的钱数÷超出2小时经过的时间,由此可以得出停车的时间,然后根据选项经过的时间作答即可。
47.B
解:616÷2=308厘米,所以这个轮胎的周长是308厘米。
故答案为:B。
从印记可以得到,616cm表示车轮滚了2周,所以这个轮胎的周长=车轮滚动2周走的距离÷2。
48.A
解:这堆纸箱从正面看是A项中的图形。
故答案为:A。
由题意可知,这堆纸箱从正面看是三列正方形,最左边一列是2个正方形,中间一列是3个正方形,最右边是1个正方形。
49.B
解:B项中的图像能表示酒面上升速度。
故答案为:B。
从图中可以看出,瓶子上面的部分比下面细,所以图像的斜率会增大。
50.C
解:6厘米=60毫米,60:5=12:1,所以这张图纸的比例尺是12:1。
故答案为:C。
先把单位进行换算,即1厘米=10毫米,那么比例尺=图上距离:实际距离。
同课章节目录
