2025年浙江省小升初数学近三年真题分类汇编专题10 计算题 30 题(含答案)
文档属性
| 名称 | 2025年浙江省小升初数学近三年真题分类汇编专题10 计算题 30 题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 176.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-03 21:33:00 | ||
图片预览



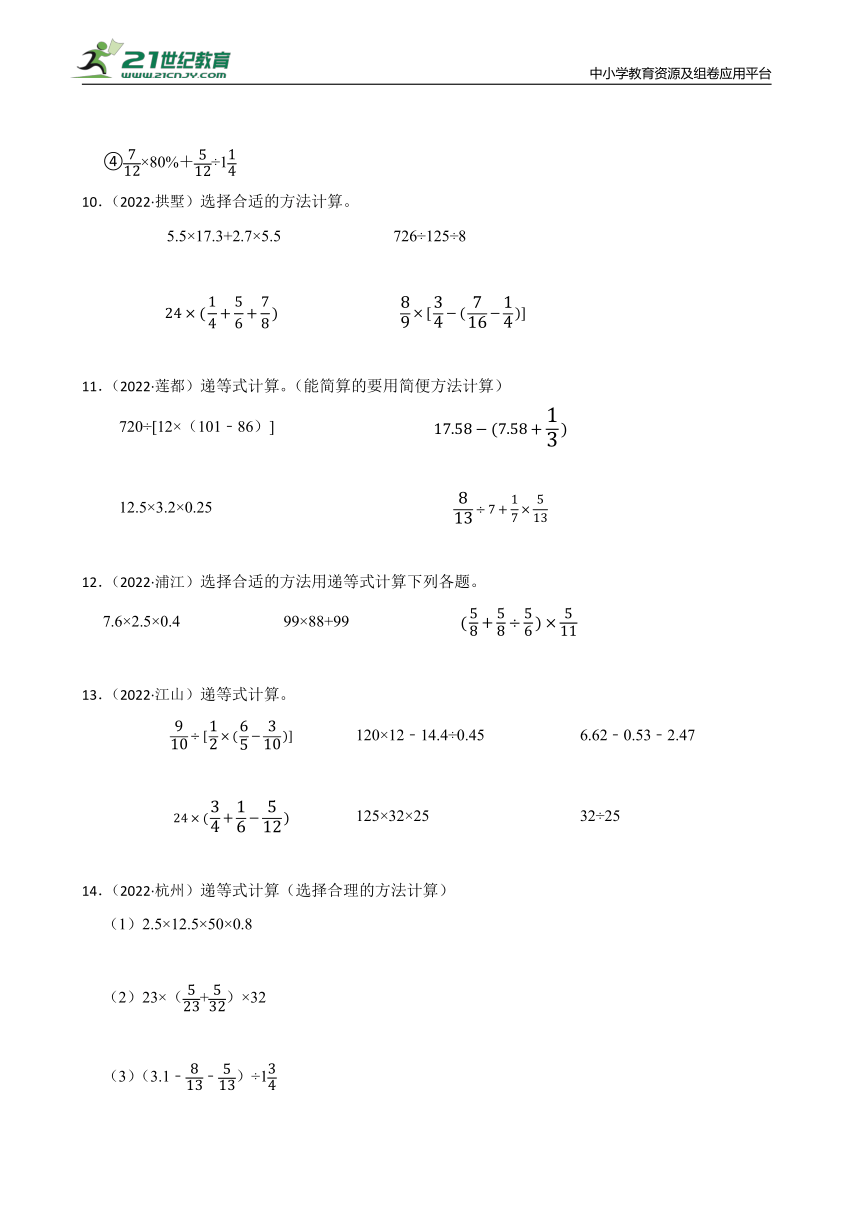

文档简介
中小学教育资源及组卷应用平台
2025年浙江省小升初数学近三年真题分类汇编
专题10 计算题 30 题
一、计算题
1.(2024·宁波)选择合适的方法计算。
①60+630÷18 ② ③
④1.25×6.4×0.25 ⑤ ⑥
2.(2024·鄞州)用合理灵活的方法计算。
2.5×12.5×50×0.8 2024÷[690÷(115﹣85)]
3.(2024·平阳)计算下面各题,能用简便算法的就用简便算法。
(1)1974﹣625÷25+75
(2)7.18﹣0.34﹣0.66
(3)
(4)
4.(2024·北仑)怎样简便怎样算。
① ②
③ ④
5.(2023·杭州) 用简便方法计等。
6.(2023·柯城)计算下面各题。能简便的要简便算
①×7+
②3.5×10.1
③×6×7×
④×[5-(+)]
⑤48×(+-)
7.(2023·长兴)用合理的方法计算。(写出主要计算过程)
① ×58﹣58×
②525+450÷15
③200﹣12.8﹣7.2
④24÷ ×( ﹣ )
⑤2.5×1.25×0.8
⑥ ×[ +( ﹣25%)]
8.(2023·椒江)用合适的方法计算下面各题(能简便的要简便计算)。
843﹣453÷15×25 1.25×17×8.8 3.16﹣+5.84﹣
26× 15﹣13÷11+×2 11.4÷[14﹣(9.54+4.08)]
9.(2023·金东)递等式计算。(能简算的要简算)
①(+-)÷
②125%×3.2×25
③19.43-(9.43+6.89)
④×80%+÷1
10.(2022·拱墅)选择合适的方法计算。
5.5×17.3+2.7×5.5 726÷125÷8
11.(2022·莲都)递等式计算。(能简算的要用简便方法计算)
720÷[12×(101﹣86)]
12.5×3.2×0.25
12.(2022·浦江)选择合适的方法用递等式计算下列各题。
7.6×2.5×0.4 99×88+99
13.(2022·江山)递等式计算。
120×12﹣14.4÷0.45 6.62﹣0.53﹣2.47
125×32×25 32÷25
14.(2022·杭州)递等式计算(选择合理的方法计算)
(1)2.5×12.5×50×0.8
(2)23×(+)×32
(3)(3.1﹣﹣)÷1
(4)17÷64×1.25+÷+9.5×125%
15.(2022·越城)脱式计算,能简算的要简算。
①40×[2-(+)]
②48×(+-)
③(2.74+5.4÷2.7)×0.3
④0.25×1.25×32
⑤507÷3+12.5×11
⑥2011×
16.(2022·镇海)用合理的方法脱式计算(能简算的要写出简算过程)
①9.375﹣4.5﹣(﹣)
②3.2×0.25×125
③÷[(﹣25%)÷]
④(+﹣)÷
⑤(3.2×1.5+2.4)÷1.6
⑥0.75×65+×34+75%
17.(2022·慈溪)脱式计算,能简便的用简便方法计算
①250-250÷25×2
②18÷ ×
③5.2÷0.4÷2.5
④(34- )÷17
⑤4.3×1.75-1.75+ ×6.7
⑥ ×[(72.8-69.6)÷ ]
18.(2022·平阳)递等式计算
(1)160+840÷20
(2)2.5×99+2.5
(3)7.23--0.25
(4)120÷[×(1-)]
19.(2022·鹿城)递等式计算,怎样简便就怎样算。
①42×()
②7.5×(26-10)+9.7
③0.8×4×12.5×2.5
④÷[1-(+0.25) ]
20.(2024·宁波)直接写出得数。
①= ②0.32÷0.1= ③5.4×= ④=
⑤﹣0.3= ⑥25×4%= ⑦= ⑧=
21.(2024·江北)直接写出得数。
422﹣199= 1.4+0.86= 0.1+0.7= 2.4×0.5= 9﹣9×0.9=
+0.2= = 5.1+= ×57%= =
22.(2024·鄞州)直接写出得数。
13×40= 6﹣0.6= 0.8×0.5= 186+24=
= = = =
23.(2024·平阳)直接写得数。
100﹣62= 4.33+0.7= 0.2×0.3= 7.2÷0.9=
= = = =
24.(2024·北仑) 直接写出得数。
= 0.24t:1.2Kg(求比值)=
25.(2023·杭州) 直接写出得数。
1.25×8=
26.(2023·柯城)计算
+= ÷8= 4--= +++= 43÷10%=
÷= ××0= 1.25+8.75= 1﹣0.625=
27.(2023·长兴)直接写出得数。
(1)24+42= (2) ﹣ = (3)0.56÷0.7= (4) ×0+ =
(5)20%×5= (6) ×6= (7)9.9n+0.1n= (8)1÷0.25÷40=
28.(2023·椒江)直接写出得数。
48÷0.12= 3.02﹣0.97= 2.5×3.8×0.04=
1000﹣299= 52﹣32= 3.14×12﹣3.14×5=
29.(2023·金东)直接算出得数。
10-6= ×2.4= 8.4÷40%= -÷=
72×= 3.1-3.01= 721÷89≈ 0.25×4÷0.25×4=
30.(2023六下·海曙)直接写出得数
0.57+4.3= ×= 73×101=
-= 2.4÷0.1= 2.6×-×0.6=
答案解析部分
1.解:①60+630÷18
=60+35
=95
②
=9.9÷(7.8-1.2)
=9.9÷6.6
=1.5
③
=××
=×()
=-×
=-
④1.25×6.4×0.25
=1.25×(0.8×8)×0.25
=(1.25×0.8)×(8×0.25)
=1×2
=2
⑤
=÷[÷]
=÷
=
⑥
=2-×
=2-
=
①先算除法,再算加法;
②小数数四则混合运算,如果有括号先算小括号里面的,再算中括号里面的,最后算括号外面的;如果没有括号,先算乘除,再算加减;只含有同一级运算,按照从左到右的顺序计算;
③应用乘法分配律,先计算()=- ,然后再乘;
④把6.4分成0.8×8,然后应用乘法交换律、乘法结合律,变成(1.25×0.8)×(8×0.25),先算括号里面的,再算括号外面的;
⑤、⑥数数四则混合运算,如果有括号先算小括号里面的,再算中括号里面的,最后算括号外面的;如果没有括号,先算乘除,再算加减;只含有同一级运算,按照从左到右的顺序计算。
2.解:2.5×12.5×50×0.8
=(2.5×50)×(12.5×0.8)
=125×10
=1250
2024÷[690÷(115﹣85)]
=2024÷[690÷30]
=2024÷23
=88
=
=
=24×+24×﹣24×
=6+20﹣21
=5
=0.8×6.5+5.5×0.8﹣2×0.8
=0.8×(6.5+5.5﹣2)
=0.8×10
=8
=
=
第一题:运用乘法交换律和结合律,把2.5与50相乘,12.5与8相乘;
第二题:先算小括号里面的减法,再算中括号里面的除法,最后计算中括号外面的除法;
第三题:运用减法的性质用第一个数减去后面两个数的和即可;
第四题:直接运用乘法分配律简便计算;
第五题:把除法转化成乘法,把分数、百分数都化成小数,然后运用乘法分配律简便计算;
第六题:先算小括号里面的减法,再算小括号外面的乘法和除法。
3.(1)1974﹣625÷25+75
=1974﹣25+75
=1974+(75﹣25)
=1974+50
=2024
(2)7.18﹣0.34﹣0.66
=7.18﹣(0.34+0.66)
=7.18﹣1
=6.18
(3)=×(102-2)
=×100
=60
(4)=
=
=
(1)先算除法,然后把后两个数相减,再加上第一个数即可;
(2)运用减法的性质,用第一个数减去后面两个数的和;
(3)直接运用乘法分配律简便计算即可;
(4)先算小括号里面的加法,再算中括号里面的乘法,最后计算中括号外面的除法。
4.解:①24×(+)
=24×+24×
=20+21
=41
②(2024+)÷2024
=2024×+×
=1+
=
③36÷+36÷1.5
=8+24
=32
④÷[0.5+(2-)]
=÷[0.5+1.25]
=÷
=
①应用乘法分配律,括号里面的数分别与括号外面的数相乘,然后再相加;
②除以一个非0的数,等于乘它的倒数;应用乘法分配律,括号里面的数分别与括号外面的数相乘,然后再相加;
③先算除法,再算加法;
④分数四则混合运算,如果有括号先算小括号里面的,再算中括号里面的,最后算括号外面的;如果没有括号,先算乘除,再算加减;只含有同一级运算,按照从左到右的顺序计算。
5.解:25×1.25×32
=(25×4)×(1.25×8)
=100×10
=1000
3.4×2.77+0.23×3.4
=(2.77+0.23)×3.4
=3×3.4
=10.2
(+)×15×17
=×15×17+×17×15
=17+30
=47
把32分成4×8,然后应用乘法交换律、乘法结合律,把(25×4)与(1.25×8)结合在一起简便运算;
应用乘法分配律,先计算2.77+0.23=3,然后把所得的和乘3.4;
应用乘法分配律括号里面的数分别与括号外面的数相乘,再把所得的积相加。
6.解:①×7+
=×(7+1)
=×8
=5
②3.5×10.1
=3.5×(10+0.1)
=3.5×10+3.5×0.1
=35+0.35
=35.35
③×6×7×
=×7×(6×)
=5×1
=5
④×[5-(+)]
=×[5-]
=×
=
⑤48×(+-)
=48×+48×-48×
=12+8-16
=4
①应用乘法分配律,先计算7+1=8,然后把所得的和乘;
②应用乘法分配律,先把10.1分成10+0.1,然后分别与3.5相乘,再把所得的积相加;
③应用乘法交换律、乘法结合律,把×5与6×分别结合在一起先计算;
④先算小括号里面的,再算中括号里面的,最后算括号外面的;
⑤应用乘法分配律,先把48分别与括号里面的数相乘,然后再相加减。
7.解:① ×58﹣58×
=58×( ﹣ )
=58×1
=58
②525+450÷15
=525+30
=555
③200﹣12.8﹣7.2
=200﹣(12.8+7.2)
=200﹣20
=180
④24÷ ×( ﹣ )
=24÷ ×1
=30
⑤2.5×1.25×0.8
=2.5×(1.25×0.8)
=2.5×1
=2.5
⑥ ×[ +( ﹣25%)]
= ×[ ﹣25%+ ]
= ×
=
①应用乘法分配律简便运算;
②、④、⑥分数、百分数四则混合运算,如果有括号先算小括号里面的,再算中括号里面的,最后算括号外面的;如果没有括号,先算乘除,再算加减;只含有同一级运算,按照从左到右的顺序计算;
③应用减法的性质简便运算;
⑤应用乘法结合律简便运算。
8.解:843-453÷15×25
=843-30.2×25
=843-755
=88
1.25×17×8.8
=1.25×(8+0.8)×17
=1.25×8×17+1.25×0.8×17
=170+17
=187
3.16-+5.84-
=(3.16+5.84)-(+)
=9-1
=8
26×
=25×+1×
=4+
=
15-13÷11+×2
=15-+
=15-(-)
=15-1
=14
11.4÷[14-(9.54+4.08)]
=11.4÷[ 14-13.62 ]
=11.4÷0.38
=30
整数四则混合运算,如果有括号先算小括号里面的,再算中括号里面的,最后算括号外面的;如果没有括号,先算乘除,再算加减;只含有同一级运算,按照从左到右的顺序计算;
把8.8分成8+0.8,然后应用乘法分配律,变成1.25×8×17+1.25×0.8×17,再计算;
应用加法交换律、加法结合律,减法的性质,变成(3.16+5.84)-(+),先算括号里面的,再算括号外面的;
把26分成25+1,分别与相乘后,再相加;
先算15-+,然后再算(-)=1,再相减。
9.解:①(+-)÷
=×36+×36-×36
=20+27-21
=47-21
=26
②125%×3.2×25
=(125%×8)×(0.4×25)
=10×10
=100
③19.43-(9.43+6.89)
=19.43-9.43-6.89
=10-6.89
=3.11
④×80%+÷
=(+)×0.8
=1×0.8
=0.8
①、④应用乘法分配律简便运算;
②应用乘法交换律、乘法结合律简便运算;
③应用减法的性质简便运算。
10.解:5.5×17.3+2.7×5.5
=5.5×(17.3+2.7)
=5.5×20
=110
726÷125÷8
=726÷(125×8)
=726÷1000
=0.726
=24×+24×+24×
=6+20+21
=47
=×[-]
=×
=
乘法分配律:a(b+c)=ab+ac;
连除的性质:a÷b÷c=a÷(b×c);
分数四则混合运算运算顺序:(1)没有括号,同级运算,从左往右依次计算;不同级运算,先算乘除法,再算加减法;(2)有括号,要先算括号里面的,再算括号外面的;
第一题因为有相同的因数5.5,可以利用乘法分配律的逆运用使计算简便;
第二题因为125与8相乘计算简便,所以可以应用连除的性质先算125与8的积计算比较简便;
第三题通过观察发现括号里面的数都能与24约分,所以应用乘法分配律可以使计算简便;
第四题有括号,先算小括号里面的,再算中括号里面,最后计算括号外面的乘法。
11.解:720÷[12×(101﹣86)]
=720÷[12×15]
=720÷180
=4
=17.58-7.58-
=10-
=
12.5×3.2×0.25
=12.5×(0.8×4)×0.25
=(12.5×0.8)×(4×0.25)
=10×1
=10
=
=
=
第一题:先算小括号里面的减法,再算中括号里面的乘法,最后计算中括号外面的除法;
第二题:运用减法的性质去掉小括号,然后按照连减的顺序计算;
第三题:把3.2写成(0.8×4),然后运用乘法结合律简便计算;
第四题:把除法转化成乘法,然后运用乘法分配律简便计算。
12.解:7.6×2.5×0.4
=7.6×(2.5×0.4)
=7.6×1
=7.6
99×88+99
=(100﹣1)×88+99
=100×88﹣88+99
=100×88+(99﹣88)
=8800+11
=8811
第一题:运用乘法结合律,先算2.5×0.4;
第二题:把第一个99写成(100-1),然后运用乘法分配律简便计算;
第三题:先算小括号里面的除法,再算小括号里面的加法,最后计算小括号外面的乘法。
13.解:[()]
()
=2
120×12﹣14.4÷0.45
=1440﹣32
=1408
6.62﹣0.53﹣2.47
=6.62﹣(0.53+2.47)
=6.62﹣3
=3.62
24×()
=242424
=18+4﹣10
=12
125×32×25
=125×8×4×25
=(125×8)×(4×25)
=1000×100
=100000
32÷25
=32÷(100÷4)
=32÷100×4
=0.32×4
=1.28
四则混合运算运算顺序与整数相同:①没有括号,同级运算,从左往右依次计算,不同级运算,先算乘、除法,再算加、减法;②有括号,先算括号里面的,再算括号外面的;
乘法分配律:a(b+c)=ab+ac;
乘法结合律:abc=a(bc);
连减的性质:a-b-c=a-(b+c);
连除的性质:a÷b÷c=a÷(b×c);
第一题:有括号先计算小括号里面的减法,再计算中括号里面的乘法,最后计算括号外面的除法;
第二题:没有括号的不同级运算,先计算乘法和除法,再计算减法;
第三题:因为0.53与2.47的和是整数,所以利用连减的性质先算0.53与2.47的和,最后再算减法计算简便;
第四题:因为24与括号里面的每一个数都能约分,所以利用乘法分配律去掉括号计算简便;
第五题:因为125与8、25与4相乘积是整千数与整百数,所以先将32拆成8×4,再利用乘法结合律计算简便;
第六题:先将25改写成100÷4的商,再利用连除的性质的逆运用去掉括号计算简便。
14.(1)解:2.5×12.5×50×0.8
=(2.5×50)×(12.5×0.8)
=125×10
=1250
(2)解:23×(+)×32
=23× ×32+32× ×23
=160+115
=275
(3)解:(3.1﹣﹣)÷1
=[3.1﹣( + )]÷1
=[3.1﹣1]÷1
=2.1÷1
=1.2
(4)解:17÷64×1.25+÷+9.5×125%
= ×1.25+ ×1.25+9.5×1.25
=( + +9.5)×1.25
=10×1.25
=12.5
(1)应用乘法交换律、乘法结合律简便运算;
(2)、(4)应用乘法分配律简便运算;
(3)分数四则混合运算,如果有括号先算小括号里面的,再算中括号里面的,最后算括号外面的;如果没有括号,先算乘除,再算加减;只含有同一级运算,按照从左到右的顺序计算。
15.解:①40×[2-( + )]
=40×(2- )
=40×2-40×
=80-54
=26
②48×( + - )
=48× +48× ﹣48×
= +4﹣3
=
③(2.74+5.4÷2.7)×0.3
=(2.74+2)×0.3
=4.74×0.3
=1.422
④0.25×1.25×32
=0.25×1.25×(8×4)
=(0.25×4)×(1.25×8)
=1×10
=10
⑤507÷3+12.5×11
=169+137.5
=306.5
⑥2011×
=(2010+1)×
=2010× +1×
=2009+
=2009
①先算小括号里面的加法,然后运用乘法分配律简便计算;
②直接运用乘法分配律简便计算;
③先算小括号里面的除法,再算小括号里面的加法,最后计算小括号外面的乘法;
④把32写成(4×8),然后运用乘法交换律、结合律,把0.25与4相乘,1.25与8相乘;
⑤先同时计算除法和乘法,再计算加法;
⑥把2011写成(2010+1),然后运用乘法分配律简便计算。
16.解:①9.375﹣4.5﹣( ﹣ )
=9.375﹣4.5﹣ +
=(9.375+ )﹣(4.5+ )
=10﹣5
=5
②3.2×0.25×125
=(0.4×0.25)×(8×125)
=0.1×1000
=100
③ ÷[( ﹣25%)÷ ]
= ÷( ÷ )
= ÷
=
④( + ﹣ )÷
=( + ﹣ )×24
= ×24+ ×24- ×24
=20+21﹣10
=31
⑤(3.2×1.5+2.4)÷1.6
=(4.8+2.4)÷1.6
=4.5
⑥0.75×65+ ×34+75%
=0.75×(65+34+1)
=0.75×100
=75
计算分数乘法时能约分的要先约分再乘;计算分数除法时要把除法转化为乘法后再计算;混合运算要先确定运算顺序再计算;百分数的计算,把百分数化成分数或小数,然后再计算。
① :先运用减法的性质把小括号去掉,然后再运用加法交换律和结合律进行简算;
② :将3.2写成4×0.8,再运用乘法交换律和结合律进行简算;
③ :先计算小括号里的减法,再计算中括号里的除法,最后算括号外的除法;
④ :先将括号外的分数除法变成分数乘法,再运用乘法分配律进行简算;
⑤ :先计算小括号里的乘法,再计算小括号里的加法,最后算括号外的除法;
⑥ :将分数和百分数转化为小数0.75,再运用乘法分配律进行简算。
17.解:①250-250÷25×2
=250-10×2
=250-20
=230
②18÷ ×
=18× ×
=27
③5.2÷0.4÷2.5
=5.2÷(0.4×2.5)
=5.2
④(34- )÷17
=(34- )×
=34× - ×
=2-
=1
⑤4.3×1.75-1.75+ ×6.7
=4.3×1.75-1.75+1.75×6.7
=1.75×(4.3-1+6.7)
=1.75×10
=17.5
⑥ ×[(72.8-69.6)÷ ]
= ×(3.2÷ )
=1.5
在没有小括号,既有加减法,又有乘除法的计算中,要先算乘除法,再算加减法;
在没有小括号,只有乘除法的计算中,要按照顺序从左往右依此计算;
连续除以两个数,等于除以这两个数的积;
乘法分配律:a×b+a×c=a×(b+c);
在既有小括号,又有中括号的计算中,要先算小括号里面的,再算中括号里面的,最后算中括号外面的。
18.(1)解:160+840÷20
=160+42
=202
(2)解:2.5×99+2.5
=2.5×(99+1)
=2.5×100
=250
(3)解:7.23- -0.25
=7.23﹣( +0.25)
=7.23﹣1
=6.23
(4)解:120÷[ ×(1- )]
=120÷[ × ]
=120÷
=450
(1)先算除法,再算加法;
(2)一个相同的数分别同两个不同的数相乘,积相加,等于这个相同的数乘另外两个不同数的和,据此简算;
(3)连续减去两个数,等于减去这两个数的和,据此进行简算;
(4)运算顺序:先算乘除,再算加减,如果有括号,就先算括号里面的。如果有小括号和中括号,由内到外,先算小括号里面的,再算中括号里面的。
19.解:①42×()
=42×+42×-42×
=7+18-15
=10
②7.5×(26-10)+9.7
=7.5×16+9.7
=120+9.7
=129.7
③0.8×4×12.5×2.5
=0.8×12.5×(4×2.5)
=10×10
=100
④÷[1-(+0.25) ]
=÷[1- ]
=÷
=4
①一个数乘几个数的和或差,等于这个数分别同这几个数相乘,再把积相加或相减,结果不变。据此简算;
②先算小括号里面的减法,再算括号外面的乘法,最后算加法;
③运用乘法交换律、乘法结合律进行简算;
④运算顺序:先算乘除,再算加减,如果有括号,就先算括号里面的。如果有小括号和中括号,由内到外,先算小括号里面的,再算中括号里面的。
20.
①= ②0.32÷0.1=3.2 ③5.4×=1.2 ④=13
⑤-0.3=0.575 ⑥25×4%=1 ⑦= ⑧=
含有百分数的计算,把百分数化成分数或小数,然后再计算;一个非0的数除以一个分数,等于这个数乘它的倒数;分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母。
21.
422-199=223 1.4+0.86=2.26 0.1+0.7=0.8 2.4×0.5=1.2 9﹣9×0.9=0.9
+0.2= = 5.1+= ×57%=0.09 =
含有百分数的计算,把百分数化成分数或小数,然后再计算;同分母分数相加减,分母不变,分子相加减;异分母分数相加减,先通分,然后按照同分母分数加减法的法则进行计算。
小数乘法,先按整数乘法算出积,再看因数中一共有几位小数,就从积的右边起数出几位,点上小数点。
22.
13×40=520 6﹣0.6=5.4 0.8×0.5=0.4 186+24=210
= =18 =0.9 =
计算小数加减法时要把小数点对齐;计算小数乘法时要注意乘积中小数的位数;计算分数乘法时能约分的要先约分再乘;计算分数除法时要把除法转化成乘法再计算;混合运算要先确定运算顺序再计算。
23.
100﹣62=38 4.33+0.7=5.03 0.2×0.3=0.06 7.2÷0.9=8
= = = =2
计算整数减法时注意退位情况;计算小数加法时注意把小数点对齐;计算小数乘除法时注意得数中小数点的位置;计算分数乘法时能约分的要先约分再乘;计算分数除法时要把除法转化成乘法再计算。
24.
105 24 3.03
2 11 =1 0.24t:1.2Kg(求比值)=200
含有百分数的计算,把百分数化成分数或小数,然后再计算;一个非0的数除以一个分数,等于这个数乘它的倒数;分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母;求比值=比的前项÷比的后项。
25.
2 1.25×8=10
1 5 28
一个非0的数除以一个分数,等于这个数乘它的倒数;分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母。
26.
+= ÷8= 4--=3 += 43÷10%=430
÷= ××0=0 1.25+8.75=10 1-0.625=0.375 9
含有百分数的计算,把百分数化成分数或小数,然后再计算;一个非0的数除以一个分数,等于这个数乘它的倒数;分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母。
27.
(1)24+42=66 (2) ﹣ = (3)0.56÷0.7=0.8 (4) ×0+ =
(5)20%×5=1 (6) ×6=2 (7)9.9n+0.1n=10n (8)1÷0.25÷40=0.1
含有百分数的计算,把百分数化成分数或小数,然后再计算;一个非0的数除以一个分数,等于这个数乘它的倒数;分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母。
28.
48÷0.12=400 3.02-0.97=2.05 2.3×3.8×0.04=0.38
1000-299=701 52-32=16 3.14×12-3.14×5=21.98
一个非0的数除以一个分数,等于这个数乘它的倒数;分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母;
异分母分数相加减,先通分,然后按照同分母分数加减法的法则进行计算。
小数乘法,先按整数乘法算出积,再看因数中一共有几位小数,就从积的右边起数出几位,点上小数点;除数是小数的除法,先移动除数的小数点,使它变成整数,除数的小数点向右移动几位,被除数的小数点也向右移动几位,然后按照除数是整数的除法进行计算。
29.
10-= ×2.4=1.8 8.4÷40%=21 -÷=
72×=63 3.1-3.01=0.09 721÷89≈80 0.25×4÷0.25×4=16
含有百分数的计算,把百分数化成分数或小数,然后再计算;一个非0的数除以一个分数,等于这个数乘它的倒数;分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母。
30.
0.57+4.3=4.87 ×= 73×101=7373
-= 2.4÷0.1=24 2.6×-×0.6=
异分母分数相加减,先通分,然后按照同分母分数加减法进行计算;
分数乘分数,能约分的先约分,然后分子和分子相乘的结果做分子,分母和分母相乘的结果做分母;
乘法分配律:一个相同的数分别同两个不同的数相乘,积相减,等于这个相同的数乘另外两个不同数的差。
2025年浙江省小升初数学近三年真题分类汇编
专题10 计算题 30 题
一、计算题
1.(2024·宁波)选择合适的方法计算。
①60+630÷18 ② ③
④1.25×6.4×0.25 ⑤ ⑥
2.(2024·鄞州)用合理灵活的方法计算。
2.5×12.5×50×0.8 2024÷[690÷(115﹣85)]
3.(2024·平阳)计算下面各题,能用简便算法的就用简便算法。
(1)1974﹣625÷25+75
(2)7.18﹣0.34﹣0.66
(3)
(4)
4.(2024·北仑)怎样简便怎样算。
① ②
③ ④
5.(2023·杭州) 用简便方法计等。
6.(2023·柯城)计算下面各题。能简便的要简便算
①×7+
②3.5×10.1
③×6×7×
④×[5-(+)]
⑤48×(+-)
7.(2023·长兴)用合理的方法计算。(写出主要计算过程)
① ×58﹣58×
②525+450÷15
③200﹣12.8﹣7.2
④24÷ ×( ﹣ )
⑤2.5×1.25×0.8
⑥ ×[ +( ﹣25%)]
8.(2023·椒江)用合适的方法计算下面各题(能简便的要简便计算)。
843﹣453÷15×25 1.25×17×8.8 3.16﹣+5.84﹣
26× 15﹣13÷11+×2 11.4÷[14﹣(9.54+4.08)]
9.(2023·金东)递等式计算。(能简算的要简算)
①(+-)÷
②125%×3.2×25
③19.43-(9.43+6.89)
④×80%+÷1
10.(2022·拱墅)选择合适的方法计算。
5.5×17.3+2.7×5.5 726÷125÷8
11.(2022·莲都)递等式计算。(能简算的要用简便方法计算)
720÷[12×(101﹣86)]
12.5×3.2×0.25
12.(2022·浦江)选择合适的方法用递等式计算下列各题。
7.6×2.5×0.4 99×88+99
13.(2022·江山)递等式计算。
120×12﹣14.4÷0.45 6.62﹣0.53﹣2.47
125×32×25 32÷25
14.(2022·杭州)递等式计算(选择合理的方法计算)
(1)2.5×12.5×50×0.8
(2)23×(+)×32
(3)(3.1﹣﹣)÷1
(4)17÷64×1.25+÷+9.5×125%
15.(2022·越城)脱式计算,能简算的要简算。
①40×[2-(+)]
②48×(+-)
③(2.74+5.4÷2.7)×0.3
④0.25×1.25×32
⑤507÷3+12.5×11
⑥2011×
16.(2022·镇海)用合理的方法脱式计算(能简算的要写出简算过程)
①9.375﹣4.5﹣(﹣)
②3.2×0.25×125
③÷[(﹣25%)÷]
④(+﹣)÷
⑤(3.2×1.5+2.4)÷1.6
⑥0.75×65+×34+75%
17.(2022·慈溪)脱式计算,能简便的用简便方法计算
①250-250÷25×2
②18÷ ×
③5.2÷0.4÷2.5
④(34- )÷17
⑤4.3×1.75-1.75+ ×6.7
⑥ ×[(72.8-69.6)÷ ]
18.(2022·平阳)递等式计算
(1)160+840÷20
(2)2.5×99+2.5
(3)7.23--0.25
(4)120÷[×(1-)]
19.(2022·鹿城)递等式计算,怎样简便就怎样算。
①42×()
②7.5×(26-10)+9.7
③0.8×4×12.5×2.5
④÷[1-(+0.25) ]
20.(2024·宁波)直接写出得数。
①= ②0.32÷0.1= ③5.4×= ④=
⑤﹣0.3= ⑥25×4%= ⑦= ⑧=
21.(2024·江北)直接写出得数。
422﹣199= 1.4+0.86= 0.1+0.7= 2.4×0.5= 9﹣9×0.9=
+0.2= = 5.1+= ×57%= =
22.(2024·鄞州)直接写出得数。
13×40= 6﹣0.6= 0.8×0.5= 186+24=
= = = =
23.(2024·平阳)直接写得数。
100﹣62= 4.33+0.7= 0.2×0.3= 7.2÷0.9=
= = = =
24.(2024·北仑) 直接写出得数。
= 0.24t:1.2Kg(求比值)=
25.(2023·杭州) 直接写出得数。
1.25×8=
26.(2023·柯城)计算
+= ÷8= 4--= +++= 43÷10%=
÷= ××0= 1.25+8.75= 1﹣0.625=
27.(2023·长兴)直接写出得数。
(1)24+42= (2) ﹣ = (3)0.56÷0.7= (4) ×0+ =
(5)20%×5= (6) ×6= (7)9.9n+0.1n= (8)1÷0.25÷40=
28.(2023·椒江)直接写出得数。
48÷0.12= 3.02﹣0.97= 2.5×3.8×0.04=
1000﹣299= 52﹣32= 3.14×12﹣3.14×5=
29.(2023·金东)直接算出得数。
10-6= ×2.4= 8.4÷40%= -÷=
72×= 3.1-3.01= 721÷89≈ 0.25×4÷0.25×4=
30.(2023六下·海曙)直接写出得数
0.57+4.3= ×= 73×101=
-= 2.4÷0.1= 2.6×-×0.6=
答案解析部分
1.解:①60+630÷18
=60+35
=95
②
=9.9÷(7.8-1.2)
=9.9÷6.6
=1.5
③
=××
=×()
=-×
=-
④1.25×6.4×0.25
=1.25×(0.8×8)×0.25
=(1.25×0.8)×(8×0.25)
=1×2
=2
⑤
=÷[÷]
=÷
=
⑥
=2-×
=2-
=
①先算除法,再算加法;
②小数数四则混合运算,如果有括号先算小括号里面的,再算中括号里面的,最后算括号外面的;如果没有括号,先算乘除,再算加减;只含有同一级运算,按照从左到右的顺序计算;
③应用乘法分配律,先计算()=- ,然后再乘;
④把6.4分成0.8×8,然后应用乘法交换律、乘法结合律,变成(1.25×0.8)×(8×0.25),先算括号里面的,再算括号外面的;
⑤、⑥数数四则混合运算,如果有括号先算小括号里面的,再算中括号里面的,最后算括号外面的;如果没有括号,先算乘除,再算加减;只含有同一级运算,按照从左到右的顺序计算。
2.解:2.5×12.5×50×0.8
=(2.5×50)×(12.5×0.8)
=125×10
=1250
2024÷[690÷(115﹣85)]
=2024÷[690÷30]
=2024÷23
=88
=
=
=24×+24×﹣24×
=6+20﹣21
=5
=0.8×6.5+5.5×0.8﹣2×0.8
=0.8×(6.5+5.5﹣2)
=0.8×10
=8
=
=
第一题:运用乘法交换律和结合律,把2.5与50相乘,12.5与8相乘;
第二题:先算小括号里面的减法,再算中括号里面的除法,最后计算中括号外面的除法;
第三题:运用减法的性质用第一个数减去后面两个数的和即可;
第四题:直接运用乘法分配律简便计算;
第五题:把除法转化成乘法,把分数、百分数都化成小数,然后运用乘法分配律简便计算;
第六题:先算小括号里面的减法,再算小括号外面的乘法和除法。
3.(1)1974﹣625÷25+75
=1974﹣25+75
=1974+(75﹣25)
=1974+50
=2024
(2)7.18﹣0.34﹣0.66
=7.18﹣(0.34+0.66)
=7.18﹣1
=6.18
(3)=×(102-2)
=×100
=60
(4)=
=
=
(1)先算除法,然后把后两个数相减,再加上第一个数即可;
(2)运用减法的性质,用第一个数减去后面两个数的和;
(3)直接运用乘法分配律简便计算即可;
(4)先算小括号里面的加法,再算中括号里面的乘法,最后计算中括号外面的除法。
4.解:①24×(+)
=24×+24×
=20+21
=41
②(2024+)÷2024
=2024×+×
=1+
=
③36÷+36÷1.5
=8+24
=32
④÷[0.5+(2-)]
=÷[0.5+1.25]
=÷
=
①应用乘法分配律,括号里面的数分别与括号外面的数相乘,然后再相加;
②除以一个非0的数,等于乘它的倒数;应用乘法分配律,括号里面的数分别与括号外面的数相乘,然后再相加;
③先算除法,再算加法;
④分数四则混合运算,如果有括号先算小括号里面的,再算中括号里面的,最后算括号外面的;如果没有括号,先算乘除,再算加减;只含有同一级运算,按照从左到右的顺序计算。
5.解:25×1.25×32
=(25×4)×(1.25×8)
=100×10
=1000
3.4×2.77+0.23×3.4
=(2.77+0.23)×3.4
=3×3.4
=10.2
(+)×15×17
=×15×17+×17×15
=17+30
=47
把32分成4×8,然后应用乘法交换律、乘法结合律,把(25×4)与(1.25×8)结合在一起简便运算;
应用乘法分配律,先计算2.77+0.23=3,然后把所得的和乘3.4;
应用乘法分配律括号里面的数分别与括号外面的数相乘,再把所得的积相加。
6.解:①×7+
=×(7+1)
=×8
=5
②3.5×10.1
=3.5×(10+0.1)
=3.5×10+3.5×0.1
=35+0.35
=35.35
③×6×7×
=×7×(6×)
=5×1
=5
④×[5-(+)]
=×[5-]
=×
=
⑤48×(+-)
=48×+48×-48×
=12+8-16
=4
①应用乘法分配律,先计算7+1=8,然后把所得的和乘;
②应用乘法分配律,先把10.1分成10+0.1,然后分别与3.5相乘,再把所得的积相加;
③应用乘法交换律、乘法结合律,把×5与6×分别结合在一起先计算;
④先算小括号里面的,再算中括号里面的,最后算括号外面的;
⑤应用乘法分配律,先把48分别与括号里面的数相乘,然后再相加减。
7.解:① ×58﹣58×
=58×( ﹣ )
=58×1
=58
②525+450÷15
=525+30
=555
③200﹣12.8﹣7.2
=200﹣(12.8+7.2)
=200﹣20
=180
④24÷ ×( ﹣ )
=24÷ ×1
=30
⑤2.5×1.25×0.8
=2.5×(1.25×0.8)
=2.5×1
=2.5
⑥ ×[ +( ﹣25%)]
= ×[ ﹣25%+ ]
= ×
=
①应用乘法分配律简便运算;
②、④、⑥分数、百分数四则混合运算,如果有括号先算小括号里面的,再算中括号里面的,最后算括号外面的;如果没有括号,先算乘除,再算加减;只含有同一级运算,按照从左到右的顺序计算;
③应用减法的性质简便运算;
⑤应用乘法结合律简便运算。
8.解:843-453÷15×25
=843-30.2×25
=843-755
=88
1.25×17×8.8
=1.25×(8+0.8)×17
=1.25×8×17+1.25×0.8×17
=170+17
=187
3.16-+5.84-
=(3.16+5.84)-(+)
=9-1
=8
26×
=25×+1×
=4+
=
15-13÷11+×2
=15-+
=15-(-)
=15-1
=14
11.4÷[14-(9.54+4.08)]
=11.4÷[ 14-13.62 ]
=11.4÷0.38
=30
整数四则混合运算,如果有括号先算小括号里面的,再算中括号里面的,最后算括号外面的;如果没有括号,先算乘除,再算加减;只含有同一级运算,按照从左到右的顺序计算;
把8.8分成8+0.8,然后应用乘法分配律,变成1.25×8×17+1.25×0.8×17,再计算;
应用加法交换律、加法结合律,减法的性质,变成(3.16+5.84)-(+),先算括号里面的,再算括号外面的;
把26分成25+1,分别与相乘后,再相加;
先算15-+,然后再算(-)=1,再相减。
9.解:①(+-)÷
=×36+×36-×36
=20+27-21
=47-21
=26
②125%×3.2×25
=(125%×8)×(0.4×25)
=10×10
=100
③19.43-(9.43+6.89)
=19.43-9.43-6.89
=10-6.89
=3.11
④×80%+÷
=(+)×0.8
=1×0.8
=0.8
①、④应用乘法分配律简便运算;
②应用乘法交换律、乘法结合律简便运算;
③应用减法的性质简便运算。
10.解:5.5×17.3+2.7×5.5
=5.5×(17.3+2.7)
=5.5×20
=110
726÷125÷8
=726÷(125×8)
=726÷1000
=0.726
=24×+24×+24×
=6+20+21
=47
=×[-]
=×
=
乘法分配律:a(b+c)=ab+ac;
连除的性质:a÷b÷c=a÷(b×c);
分数四则混合运算运算顺序:(1)没有括号,同级运算,从左往右依次计算;不同级运算,先算乘除法,再算加减法;(2)有括号,要先算括号里面的,再算括号外面的;
第一题因为有相同的因数5.5,可以利用乘法分配律的逆运用使计算简便;
第二题因为125与8相乘计算简便,所以可以应用连除的性质先算125与8的积计算比较简便;
第三题通过观察发现括号里面的数都能与24约分,所以应用乘法分配律可以使计算简便;
第四题有括号,先算小括号里面的,再算中括号里面,最后计算括号外面的乘法。
11.解:720÷[12×(101﹣86)]
=720÷[12×15]
=720÷180
=4
=17.58-7.58-
=10-
=
12.5×3.2×0.25
=12.5×(0.8×4)×0.25
=(12.5×0.8)×(4×0.25)
=10×1
=10
=
=
=
第一题:先算小括号里面的减法,再算中括号里面的乘法,最后计算中括号外面的除法;
第二题:运用减法的性质去掉小括号,然后按照连减的顺序计算;
第三题:把3.2写成(0.8×4),然后运用乘法结合律简便计算;
第四题:把除法转化成乘法,然后运用乘法分配律简便计算。
12.解:7.6×2.5×0.4
=7.6×(2.5×0.4)
=7.6×1
=7.6
99×88+99
=(100﹣1)×88+99
=100×88﹣88+99
=100×88+(99﹣88)
=8800+11
=8811
第一题:运用乘法结合律,先算2.5×0.4;
第二题:把第一个99写成(100-1),然后运用乘法分配律简便计算;
第三题:先算小括号里面的除法,再算小括号里面的加法,最后计算小括号外面的乘法。
13.解:[()]
()
=2
120×12﹣14.4÷0.45
=1440﹣32
=1408
6.62﹣0.53﹣2.47
=6.62﹣(0.53+2.47)
=6.62﹣3
=3.62
24×()
=242424
=18+4﹣10
=12
125×32×25
=125×8×4×25
=(125×8)×(4×25)
=1000×100
=100000
32÷25
=32÷(100÷4)
=32÷100×4
=0.32×4
=1.28
四则混合运算运算顺序与整数相同:①没有括号,同级运算,从左往右依次计算,不同级运算,先算乘、除法,再算加、减法;②有括号,先算括号里面的,再算括号外面的;
乘法分配律:a(b+c)=ab+ac;
乘法结合律:abc=a(bc);
连减的性质:a-b-c=a-(b+c);
连除的性质:a÷b÷c=a÷(b×c);
第一题:有括号先计算小括号里面的减法,再计算中括号里面的乘法,最后计算括号外面的除法;
第二题:没有括号的不同级运算,先计算乘法和除法,再计算减法;
第三题:因为0.53与2.47的和是整数,所以利用连减的性质先算0.53与2.47的和,最后再算减法计算简便;
第四题:因为24与括号里面的每一个数都能约分,所以利用乘法分配律去掉括号计算简便;
第五题:因为125与8、25与4相乘积是整千数与整百数,所以先将32拆成8×4,再利用乘法结合律计算简便;
第六题:先将25改写成100÷4的商,再利用连除的性质的逆运用去掉括号计算简便。
14.(1)解:2.5×12.5×50×0.8
=(2.5×50)×(12.5×0.8)
=125×10
=1250
(2)解:23×(+)×32
=23× ×32+32× ×23
=160+115
=275
(3)解:(3.1﹣﹣)÷1
=[3.1﹣( + )]÷1
=[3.1﹣1]÷1
=2.1÷1
=1.2
(4)解:17÷64×1.25+÷+9.5×125%
= ×1.25+ ×1.25+9.5×1.25
=( + +9.5)×1.25
=10×1.25
=12.5
(1)应用乘法交换律、乘法结合律简便运算;
(2)、(4)应用乘法分配律简便运算;
(3)分数四则混合运算,如果有括号先算小括号里面的,再算中括号里面的,最后算括号外面的;如果没有括号,先算乘除,再算加减;只含有同一级运算,按照从左到右的顺序计算。
15.解:①40×[2-( + )]
=40×(2- )
=40×2-40×
=80-54
=26
②48×( + - )
=48× +48× ﹣48×
= +4﹣3
=
③(2.74+5.4÷2.7)×0.3
=(2.74+2)×0.3
=4.74×0.3
=1.422
④0.25×1.25×32
=0.25×1.25×(8×4)
=(0.25×4)×(1.25×8)
=1×10
=10
⑤507÷3+12.5×11
=169+137.5
=306.5
⑥2011×
=(2010+1)×
=2010× +1×
=2009+
=2009
①先算小括号里面的加法,然后运用乘法分配律简便计算;
②直接运用乘法分配律简便计算;
③先算小括号里面的除法,再算小括号里面的加法,最后计算小括号外面的乘法;
④把32写成(4×8),然后运用乘法交换律、结合律,把0.25与4相乘,1.25与8相乘;
⑤先同时计算除法和乘法,再计算加法;
⑥把2011写成(2010+1),然后运用乘法分配律简便计算。
16.解:①9.375﹣4.5﹣( ﹣ )
=9.375﹣4.5﹣ +
=(9.375+ )﹣(4.5+ )
=10﹣5
=5
②3.2×0.25×125
=(0.4×0.25)×(8×125)
=0.1×1000
=100
③ ÷[( ﹣25%)÷ ]
= ÷( ÷ )
= ÷
=
④( + ﹣ )÷
=( + ﹣ )×24
= ×24+ ×24- ×24
=20+21﹣10
=31
⑤(3.2×1.5+2.4)÷1.6
=(4.8+2.4)÷1.6
=4.5
⑥0.75×65+ ×34+75%
=0.75×(65+34+1)
=0.75×100
=75
计算分数乘法时能约分的要先约分再乘;计算分数除法时要把除法转化为乘法后再计算;混合运算要先确定运算顺序再计算;百分数的计算,把百分数化成分数或小数,然后再计算。
① :先运用减法的性质把小括号去掉,然后再运用加法交换律和结合律进行简算;
② :将3.2写成4×0.8,再运用乘法交换律和结合律进行简算;
③ :先计算小括号里的减法,再计算中括号里的除法,最后算括号外的除法;
④ :先将括号外的分数除法变成分数乘法,再运用乘法分配律进行简算;
⑤ :先计算小括号里的乘法,再计算小括号里的加法,最后算括号外的除法;
⑥ :将分数和百分数转化为小数0.75,再运用乘法分配律进行简算。
17.解:①250-250÷25×2
=250-10×2
=250-20
=230
②18÷ ×
=18× ×
=27
③5.2÷0.4÷2.5
=5.2÷(0.4×2.5)
=5.2
④(34- )÷17
=(34- )×
=34× - ×
=2-
=1
⑤4.3×1.75-1.75+ ×6.7
=4.3×1.75-1.75+1.75×6.7
=1.75×(4.3-1+6.7)
=1.75×10
=17.5
⑥ ×[(72.8-69.6)÷ ]
= ×(3.2÷ )
=1.5
在没有小括号,既有加减法,又有乘除法的计算中,要先算乘除法,再算加减法;
在没有小括号,只有乘除法的计算中,要按照顺序从左往右依此计算;
连续除以两个数,等于除以这两个数的积;
乘法分配律:a×b+a×c=a×(b+c);
在既有小括号,又有中括号的计算中,要先算小括号里面的,再算中括号里面的,最后算中括号外面的。
18.(1)解:160+840÷20
=160+42
=202
(2)解:2.5×99+2.5
=2.5×(99+1)
=2.5×100
=250
(3)解:7.23- -0.25
=7.23﹣( +0.25)
=7.23﹣1
=6.23
(4)解:120÷[ ×(1- )]
=120÷[ × ]
=120÷
=450
(1)先算除法,再算加法;
(2)一个相同的数分别同两个不同的数相乘,积相加,等于这个相同的数乘另外两个不同数的和,据此简算;
(3)连续减去两个数,等于减去这两个数的和,据此进行简算;
(4)运算顺序:先算乘除,再算加减,如果有括号,就先算括号里面的。如果有小括号和中括号,由内到外,先算小括号里面的,再算中括号里面的。
19.解:①42×()
=42×+42×-42×
=7+18-15
=10
②7.5×(26-10)+9.7
=7.5×16+9.7
=120+9.7
=129.7
③0.8×4×12.5×2.5
=0.8×12.5×(4×2.5)
=10×10
=100
④÷[1-(+0.25) ]
=÷[1- ]
=÷
=4
①一个数乘几个数的和或差,等于这个数分别同这几个数相乘,再把积相加或相减,结果不变。据此简算;
②先算小括号里面的减法,再算括号外面的乘法,最后算加法;
③运用乘法交换律、乘法结合律进行简算;
④运算顺序:先算乘除,再算加减,如果有括号,就先算括号里面的。如果有小括号和中括号,由内到外,先算小括号里面的,再算中括号里面的。
20.
①= ②0.32÷0.1=3.2 ③5.4×=1.2 ④=13
⑤-0.3=0.575 ⑥25×4%=1 ⑦= ⑧=
含有百分数的计算,把百分数化成分数或小数,然后再计算;一个非0的数除以一个分数,等于这个数乘它的倒数;分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母。
21.
422-199=223 1.4+0.86=2.26 0.1+0.7=0.8 2.4×0.5=1.2 9﹣9×0.9=0.9
+0.2= = 5.1+= ×57%=0.09 =
含有百分数的计算,把百分数化成分数或小数,然后再计算;同分母分数相加减,分母不变,分子相加减;异分母分数相加减,先通分,然后按照同分母分数加减法的法则进行计算。
小数乘法,先按整数乘法算出积,再看因数中一共有几位小数,就从积的右边起数出几位,点上小数点。
22.
13×40=520 6﹣0.6=5.4 0.8×0.5=0.4 186+24=210
= =18 =0.9 =
计算小数加减法时要把小数点对齐;计算小数乘法时要注意乘积中小数的位数;计算分数乘法时能约分的要先约分再乘;计算分数除法时要把除法转化成乘法再计算;混合运算要先确定运算顺序再计算。
23.
100﹣62=38 4.33+0.7=5.03 0.2×0.3=0.06 7.2÷0.9=8
= = = =2
计算整数减法时注意退位情况;计算小数加法时注意把小数点对齐;计算小数乘除法时注意得数中小数点的位置;计算分数乘法时能约分的要先约分再乘;计算分数除法时要把除法转化成乘法再计算。
24.
105 24 3.03
2 11 =1 0.24t:1.2Kg(求比值)=200
含有百分数的计算,把百分数化成分数或小数,然后再计算;一个非0的数除以一个分数,等于这个数乘它的倒数;分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母;求比值=比的前项÷比的后项。
25.
2 1.25×8=10
1 5 28
一个非0的数除以一个分数,等于这个数乘它的倒数;分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母。
26.
+= ÷8= 4--=3 += 43÷10%=430
÷= ××0=0 1.25+8.75=10 1-0.625=0.375 9
含有百分数的计算,把百分数化成分数或小数,然后再计算;一个非0的数除以一个分数,等于这个数乘它的倒数;分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母。
27.
(1)24+42=66 (2) ﹣ = (3)0.56÷0.7=0.8 (4) ×0+ =
(5)20%×5=1 (6) ×6=2 (7)9.9n+0.1n=10n (8)1÷0.25÷40=0.1
含有百分数的计算,把百分数化成分数或小数,然后再计算;一个非0的数除以一个分数,等于这个数乘它的倒数;分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母。
28.
48÷0.12=400 3.02-0.97=2.05 2.3×3.8×0.04=0.38
1000-299=701 52-32=16 3.14×12-3.14×5=21.98
一个非0的数除以一个分数,等于这个数乘它的倒数;分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母;
异分母分数相加减,先通分,然后按照同分母分数加减法的法则进行计算。
小数乘法,先按整数乘法算出积,再看因数中一共有几位小数,就从积的右边起数出几位,点上小数点;除数是小数的除法,先移动除数的小数点,使它变成整数,除数的小数点向右移动几位,被除数的小数点也向右移动几位,然后按照除数是整数的除法进行计算。
29.
10-= ×2.4=1.8 8.4÷40%=21 -÷=
72×=63 3.1-3.01=0.09 721÷89≈80 0.25×4÷0.25×4=16
含有百分数的计算,把百分数化成分数或小数,然后再计算;一个非0的数除以一个分数,等于这个数乘它的倒数;分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母。
30.
0.57+4.3=4.87 ×= 73×101=7373
-= 2.4÷0.1=24 2.6×-×0.6=
异分母分数相加减,先通分,然后按照同分母分数加减法进行计算;
分数乘分数,能约分的先约分,然后分子和分子相乘的结果做分子,分母和分母相乘的结果做分母;
乘法分配律:一个相同的数分别同两个不同的数相乘,积相减,等于这个相同的数乘另外两个不同数的差。
同课章节目录
