第6章 变量之间的关系 章末复习 课件(共39张PPT)
文档属性
| 名称 | 第6章 变量之间的关系 章末复习 课件(共39张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-05 00:00:00 | ||
图片预览











文档简介
(共39张PPT)
章末复习
第六章 变量之间的关系
北师大版(2024)数学七年级下册
授课教师:********
班 级:********
时 间:********
幂的乘方教案
一、教学目标
知识与技能目标
理解幂的乘方的运算法则。
能够熟练运用幂的乘方运算法则进行计算。
过程与方法目标
通过对幂的乘方运算法则的推导过程,培养学生的逻辑推理能力和抽象思维能力。
经历从特殊到一般的探究过程,体会数学中的归纳思想。
情感态度与价值观目标
培养学生积极参与数学活动,勇于探索的精神,激发学生对数学的兴趣。
二、教学重难点
重点
幂的乘方运算法则的理解与掌握。
运用幂的乘方运算法则进行准确计算。
难点
幂的乘方运算法则的推导过程及灵活运用。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)复习引入(5 分钟)
提问学生同底数幂的乘法法则:\(a^m×a^n = a^{m + n}\)(\(m\)、\(n\)都是正整数),并举例让学生计算,如\(2^3×2^4\)。
引出本节课主题:在幂的运算中,还有一种常见的形式,即幂的乘方,如\((a^m)^n\),这就是我们今天要学习的内容。
(二)探究新知(20 分钟)
计算以下式子:
\((2^3)^2\),引导学生根据乘方的意义展开:\(2^3×2^3 = 2^{3 + 3} = 2^6\)。
\((3^2)^4\),同样根据乘方意义展开:\(3^2×3^2×3^2×3^2 = 3^{2 + 2 + 2 + 2} = 3^8\)。
让学生观察这两个式子的计算过程和结果,提出问题:从这些计算中,你能发现幂的乘方有什么规律吗?
引导学生归纳出幂的乘方运算法则:\((a^m)^n = a^{mn}\)(\(m\)、\(n\)都是正整数)。即幂的乘方,底数不变,指数相乘。
对法则进行推导:
根据乘方的意义,\((a^m)^n\)表示\(n\)个\(a^m\)相乘,即\((a^m)^n = a^m×a^m×···×a^m\)(\(n\)个\(a^m\))。
再根据同底数幂的乘法法则,\(a^m×a^m×···×a^m = a^{m + m + ··· + m}\)(\(n\)个\(m\)相加)。
而\(n\)个\(m\)相加等于\(mn
\),所以\((a^m)^n = a^{mn}\)。
(三)例题讲解(15 分钟)
例 1:计算\((10^3)^5\)
解:根据幂的乘方运算法则,\((10^3)^5 = 10^{3×5} = 10^{15}\)。
例 2:计算\((a^4)^3\)
解:\((a^4)^3 = a^{4×3} = a^{12}\)。
例 3:计算\([(-2)^3]^4\)
解:\([(-2)^3]^4 = (-2)^{3×4} = (-2)^{12} = 2^{12}\)(负数的偶次幂是正数)。
(四)课堂练习(10 分钟)
计算:
\((5^2)^3\)
\((a^3)^4\)
\([( - 3)^2]^5\)
\((x^m)^5\)(\(m\)为正整数)
学生独立完成练习,教师巡视指导,及时纠正学生的错误。
(五)课堂小结(5 分钟)
与学生一起回顾幂的乘方运算法则:\((a^m)^n = a^{mn}\)(\(m\)、\(n\)都是正整数),强调底数不变,指数相乘。
总结幂的乘方运算法则的推导过程和应用时的注意事项。
(六)布置作业(5 分钟)
课本课后习题中关于幂的乘方的相关题目。
拓展题:已知\(a^m = 3\),\(a^n = 2\),求\((a^{2m})^3\)和\((a^{3n})^2\)的值。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
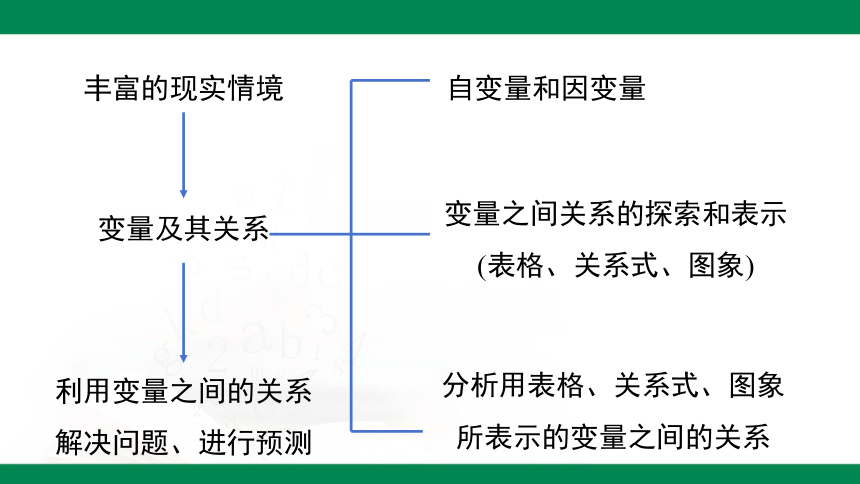
丰富的现实情境
变量及其关系
利用变量之间的关系解决问题、进行预测
自变量和因变量
变量之间关系的探索和表示(表格、关系式、图象)
分析用表格、关系式、图象所表示的变量之间的关系
一、变量与常量
1.常量:在某个变化过程中,数值始终不变的量叫作常量.
变量:在某个变化过程中,数值发生变化的量叫作变量.
2.自变量和因变量
在某个变化过程中,如果有两个变量x,y,并且变量y随着变量x的变化而变化,那么我们就说x是自变量,y是因变量.
在变化过程中起主导作用的那个变量是自变量.
二、用表格表示变量之间的关系
1.观察表格三步骤
(1)通过表格确定自变量与因变量(一般有两行,第一行表示自变量,第二行表示因变量);
(2)纵向观察每一列,发现因变量与自变量的对应关系;
(3)分别观察横向两栏,从中发现因变量随自变量的变化而呈现的变化趋势.
2.用表格表示两个变量之间关系的优缺点
(1)优点:直接,可以直接从表格中找出自变量和因变量的对应值;
(2)缺点:具有局限性,不能全面准确地反映两个变量之间的关系,只能反映其中的一部分,因此从这部分数据中观察因变量随自变量的变化而变化的趋势时,需要对表格中的数据进行分析.
三、用关系式表示两个变量之间的关系
1.关系式法:两个变量之间的关系有时可以用一个含有两个变量及数学运算符号的等式来表示,这种表示变量之间关系的方法叫作关系式法.
2.求两个变量之间关系式的常用方法:
(1)利用公式:如图形的周长公式、面积公式、体积公式等;
(2)利用生活中特定的数量关系,
(3)根据表格与图象中的信息列关系式等.
3.根据关系式求值
根据关系式求值包括两种情况:
(1)已知自变量的值求因变量的值,相当于求代数式的值;
(2)已知因变量的值求自变量的值,相当于解方程.
四、用图象表示变量之间的关系
1.图象法:用图象来表示两个变量之间关系的方法叫作图象法.
在用图象表示变量之间的关系时,通常用水平方向的数轴(称为横轴)上的点表示自变量,用竖直方向的数轴(称为纵轴)上的点表示因变量.
图象上的每一点都表示自变量和因变量之间的相互关系.
2.用图象法表示两个变量间关系的优缺点
优点:能直观、形象地反映变量间的变化情况并预测变化趋势.
缺点:只能反映变量间的部分关系,且难以得到准确的对应值.
3.图象的识图技巧
(1)注意两数轴上的名称与单位;
(2)分布规律:横轴上的点表示自变量,纵轴上的点表示因变量;
(3)识图关键:弄清图象上点的意义,找准关键点,注意图象的起点、终点、最高点、最低点、拐点等特殊位置,并弄清这些点所表示的意义.
4.探究速度随时间的变化
加速
速度v
时间t
速度v
时间t
减速
速度v
时间t
匀速
0
0
0
变化速率相同
变化速率相同
速度v
时间t
静止
速度v
时间t
减速
加速
0
0
变化速率不同
速度v
时间t
0
变化速率不同
5.探究距离随时间的变化
距离s
时间t
距离s
时间t
距离s
时间t
匀速
匀速
静止
渐行渐远
回到原地
0
0
0
距离s
时间t
静止
距离s
时间t
变速
加速
距离s
时间t
变速
减速
0
0
0
回到原地
渐行渐远
考点1 常量、变量、自变量和因变量
1. 第31届中国国际广告节于2024年11月28日在厦门正式开幕,
王先生开车去参会,途中他到加油站加油,如图是加油机上
的数据显示牌,金额随着数量的变化而变化,则下列判断正
确的是( )
D
A. 18和8.19是常量
B. 金额是自变量
C. 单价是因变量
D. 金额、数量是变量,单价是常量
返回
考点2 用表格表示变量之间的关系
2.父亲告诉小明:“距离地面越高,温度越低,”并给小明出
示了下面的表格.
距离地面的高度/ 0 1 2 3 4 5
温度/ 20 14 8 2
根据上表,父亲还给小明出了下面几个问题,你和小明一起
回答.
(1)上表反映了哪两个变量之间的关系?哪个是自变量?
哪个是因变量?
【解】反映了温度和距离地面的高度两个变量之间的关系.距
离地面的高度是自变量,温度是因变量.
(2)如果用表示距离地面的高度,用 表示温度,那么随
着的变化, 是怎么变化的?
【解】如果用表示距离地面的高度,用 表示温度,那么
随着高度的增大,温度 逐渐减小(或降低).
(3)你能猜出距离地面 的高空温度是多少吗?
距离地面的高空温度是 .
返回
考点3 用关系式表示变量之间的关系
3.长方形的长是20,宽是,周长是,面积是 .
(1)写出和 之间的关系式.
【解】由长方形的周长公式,得 .
(2)写出和 之间的关系式.
由长方形的面积公式,得 .
(3)当时,等于多少? 等于多少?
【解】当时,,解得.将 代入
,得 .
(4)当增加1时,增加多少? 增加多少?
当增加1时,.所以当 增加1时,
增加20;当增加1时, ,
所以当增加1时, 增加2.
返回
考点4 用图象表示变量之间的关系
4. 张老师在化学实验室做
实验时,将一杯 的开水放在石棉网上自
然冷却,如图是这杯水冷却时的温度变化图,
根据图中的信息,下列说法不正确的是 ( )
C
A. 水温从逐渐下降到时用了
B. 从开始冷却后时的水温是
C. 实验室的室内温度是
D. 水被自然冷却到了
返回
5. 教材P156素材 如图是某地冬季一天的气温随时间变
化的图象,根据图象回答下列问题:
(1)8时,12时,22时的气温各是多少?
【解】8时,12时,22时的气温分别是,, .
(2)这一天的最高气温是多少?几
时达到的?最低气温呢?
【解】这一天的最高气温是 ,
14时达到的,最低气温是 ,
4时达到的.
(3)这一天的温差是多少?从最低到最高气温经过多长时间?
【解】这一天的温差为,从最低到最高气温经过 .
(4)在什么范围内气温上升?在什么时间范围内气温下降?
【解】在4时时气温上升,在0时时,14时 时气温下降.
(5)图中的点表示什么? 点呢?
点表示8时的气温为;点表示24时的气温为 .
(6)在哪一时刻气温为和 ?
【解】在0时和6时的气温为;在12时和23时的气温为 .
(7)你能预测次日凌晨2时的气温吗?
【解】次日凌晨2时的气温约为 (大致范围).
返回
思想1 数形结合思想
6. 骆驼被称为“沙漠之舟”,它的体
温随时间的变化而发生较大变化,
其体温 与时间(时)之间的关系
D
如图①所示.小清同学根据图①绘制了图②,则图②中的变量
最有可能表示的是 ( )
A. 骆驼在 时刻的体温与0时体温的绝对差(即差的绝对值)
B. 骆驼从0时到 时刻之间的最高体温与当日最低体温的差
C. 骆驼在 时刻的体温与当日平均体温的绝对差
D. 骆驼从0时到 时刻之间的体温最大值与最小值的差
【点拨】从0时到4时,温差随时间
的增大而增大,在4时达到最大,是
;从4时到8时,这段时间的最
高体温是,最低体温是 ,
温差不变,从8时开始,最高体温变大,最低体温不变是
,温差变大,达到 ,从16时开始到24时体温下降,
温差不变.即变量最有可能表示的是骆驼从0时到 时刻之间
的体温最大值与最小值的差.
返回
思想2 分类讨论思想
7.[2024济南期末] 甲、乙两车分别从, 两
地同时出发,甲车匀速前往地,到达 地
后停止;乙车匀速前往地,到达 地立即
以另一速度按原路匀速返回到地,返回到 地时停止.设甲、
乙两车距地的路程为(千米),乙车行驶的时间为
(时),与 之间的图象如图所示.
(1)乙车从地返回 地的速度是_____千米/时;
(2)乙车到达地时甲车距 地的路程是
_____千米;
100
100
(3)求乙车返回前甲、乙两车相距40千米时,乙车行驶的
时间.
【解】由图象易知甲车的速度为80千米/
时,乙车从地到 地的速度为120千米/
时,当乙车返回前甲、乙两车相距40千
米时,
设乙车行驶的时间为 小时,甲、乙两车相遇之前:
,
解得 ;
甲、乙两车相遇之后:
,
解得 .
综上所述,乙车返回前甲、乙两车相距
40千米时,乙车行驶的时间为1.3小时或
1.7小时.
返回
谢谢观看!
◆懂得学习的人不如喜爱学习的人,喜爱学习的人不如以学习为乐的人.
章末复习
第六章 变量之间的关系
北师大版(2024)数学七年级下册
授课教师:********
班 级:********
时 间:********
幂的乘方教案
一、教学目标
知识与技能目标
理解幂的乘方的运算法则。
能够熟练运用幂的乘方运算法则进行计算。
过程与方法目标
通过对幂的乘方运算法则的推导过程,培养学生的逻辑推理能力和抽象思维能力。
经历从特殊到一般的探究过程,体会数学中的归纳思想。
情感态度与价值观目标
培养学生积极参与数学活动,勇于探索的精神,激发学生对数学的兴趣。
二、教学重难点
重点
幂的乘方运算法则的理解与掌握。
运用幂的乘方运算法则进行准确计算。
难点
幂的乘方运算法则的推导过程及灵活运用。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)复习引入(5 分钟)
提问学生同底数幂的乘法法则:\(a^m×a^n = a^{m + n}\)(\(m\)、\(n\)都是正整数),并举例让学生计算,如\(2^3×2^4\)。
引出本节课主题:在幂的运算中,还有一种常见的形式,即幂的乘方,如\((a^m)^n\),这就是我们今天要学习的内容。
(二)探究新知(20 分钟)
计算以下式子:
\((2^3)^2\),引导学生根据乘方的意义展开:\(2^3×2^3 = 2^{3 + 3} = 2^6\)。
\((3^2)^4\),同样根据乘方意义展开:\(3^2×3^2×3^2×3^2 = 3^{2 + 2 + 2 + 2} = 3^8\)。
让学生观察这两个式子的计算过程和结果,提出问题:从这些计算中,你能发现幂的乘方有什么规律吗?
引导学生归纳出幂的乘方运算法则:\((a^m)^n = a^{mn}\)(\(m\)、\(n\)都是正整数)。即幂的乘方,底数不变,指数相乘。
对法则进行推导:
根据乘方的意义,\((a^m)^n\)表示\(n\)个\(a^m\)相乘,即\((a^m)^n = a^m×a^m×···×a^m\)(\(n\)个\(a^m\))。
再根据同底数幂的乘法法则,\(a^m×a^m×···×a^m = a^{m + m + ··· + m}\)(\(n\)个\(m\)相加)。
而\(n\)个\(m\)相加等于\(mn
\),所以\((a^m)^n = a^{mn}\)。
(三)例题讲解(15 分钟)
例 1:计算\((10^3)^5\)
解:根据幂的乘方运算法则,\((10^3)^5 = 10^{3×5} = 10^{15}\)。
例 2:计算\((a^4)^3\)
解:\((a^4)^3 = a^{4×3} = a^{12}\)。
例 3:计算\([(-2)^3]^4\)
解:\([(-2)^3]^4 = (-2)^{3×4} = (-2)^{12} = 2^{12}\)(负数的偶次幂是正数)。
(四)课堂练习(10 分钟)
计算:
\((5^2)^3\)
\((a^3)^4\)
\([( - 3)^2]^5\)
\((x^m)^5\)(\(m\)为正整数)
学生独立完成练习,教师巡视指导,及时纠正学生的错误。
(五)课堂小结(5 分钟)
与学生一起回顾幂的乘方运算法则:\((a^m)^n = a^{mn}\)(\(m\)、\(n\)都是正整数),强调底数不变,指数相乘。
总结幂的乘方运算法则的推导过程和应用时的注意事项。
(六)布置作业(5 分钟)
课本课后习题中关于幂的乘方的相关题目。
拓展题:已知\(a^m = 3\),\(a^n = 2\),求\((a^{2m})^3\)和\((a^{3n})^2\)的值。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
丰富的现实情境
变量及其关系
利用变量之间的关系解决问题、进行预测
自变量和因变量
变量之间关系的探索和表示(表格、关系式、图象)
分析用表格、关系式、图象所表示的变量之间的关系
一、变量与常量
1.常量:在某个变化过程中,数值始终不变的量叫作常量.
变量:在某个变化过程中,数值发生变化的量叫作变量.
2.自变量和因变量
在某个变化过程中,如果有两个变量x,y,并且变量y随着变量x的变化而变化,那么我们就说x是自变量,y是因变量.
在变化过程中起主导作用的那个变量是自变量.
二、用表格表示变量之间的关系
1.观察表格三步骤
(1)通过表格确定自变量与因变量(一般有两行,第一行表示自变量,第二行表示因变量);
(2)纵向观察每一列,发现因变量与自变量的对应关系;
(3)分别观察横向两栏,从中发现因变量随自变量的变化而呈现的变化趋势.
2.用表格表示两个变量之间关系的优缺点
(1)优点:直接,可以直接从表格中找出自变量和因变量的对应值;
(2)缺点:具有局限性,不能全面准确地反映两个变量之间的关系,只能反映其中的一部分,因此从这部分数据中观察因变量随自变量的变化而变化的趋势时,需要对表格中的数据进行分析.
三、用关系式表示两个变量之间的关系
1.关系式法:两个变量之间的关系有时可以用一个含有两个变量及数学运算符号的等式来表示,这种表示变量之间关系的方法叫作关系式法.
2.求两个变量之间关系式的常用方法:
(1)利用公式:如图形的周长公式、面积公式、体积公式等;
(2)利用生活中特定的数量关系,
(3)根据表格与图象中的信息列关系式等.
3.根据关系式求值
根据关系式求值包括两种情况:
(1)已知自变量的值求因变量的值,相当于求代数式的值;
(2)已知因变量的值求自变量的值,相当于解方程.
四、用图象表示变量之间的关系
1.图象法:用图象来表示两个变量之间关系的方法叫作图象法.
在用图象表示变量之间的关系时,通常用水平方向的数轴(称为横轴)上的点表示自变量,用竖直方向的数轴(称为纵轴)上的点表示因变量.
图象上的每一点都表示自变量和因变量之间的相互关系.
2.用图象法表示两个变量间关系的优缺点
优点:能直观、形象地反映变量间的变化情况并预测变化趋势.
缺点:只能反映变量间的部分关系,且难以得到准确的对应值.
3.图象的识图技巧
(1)注意两数轴上的名称与单位;
(2)分布规律:横轴上的点表示自变量,纵轴上的点表示因变量;
(3)识图关键:弄清图象上点的意义,找准关键点,注意图象的起点、终点、最高点、最低点、拐点等特殊位置,并弄清这些点所表示的意义.
4.探究速度随时间的变化
加速
速度v
时间t
速度v
时间t
减速
速度v
时间t
匀速
0
0
0
变化速率相同
变化速率相同
速度v
时间t
静止
速度v
时间t
减速
加速
0
0
变化速率不同
速度v
时间t
0
变化速率不同
5.探究距离随时间的变化
距离s
时间t
距离s
时间t
距离s
时间t
匀速
匀速
静止
渐行渐远
回到原地
0
0
0
距离s
时间t
静止
距离s
时间t
变速
加速
距离s
时间t
变速
减速
0
0
0
回到原地
渐行渐远
考点1 常量、变量、自变量和因变量
1. 第31届中国国际广告节于2024年11月28日在厦门正式开幕,
王先生开车去参会,途中他到加油站加油,如图是加油机上
的数据显示牌,金额随着数量的变化而变化,则下列判断正
确的是( )
D
A. 18和8.19是常量
B. 金额是自变量
C. 单价是因变量
D. 金额、数量是变量,单价是常量
返回
考点2 用表格表示变量之间的关系
2.父亲告诉小明:“距离地面越高,温度越低,”并给小明出
示了下面的表格.
距离地面的高度/ 0 1 2 3 4 5
温度/ 20 14 8 2
根据上表,父亲还给小明出了下面几个问题,你和小明一起
回答.
(1)上表反映了哪两个变量之间的关系?哪个是自变量?
哪个是因变量?
【解】反映了温度和距离地面的高度两个变量之间的关系.距
离地面的高度是自变量,温度是因变量.
(2)如果用表示距离地面的高度,用 表示温度,那么随
着的变化, 是怎么变化的?
【解】如果用表示距离地面的高度,用 表示温度,那么
随着高度的增大,温度 逐渐减小(或降低).
(3)你能猜出距离地面 的高空温度是多少吗?
距离地面的高空温度是 .
返回
考点3 用关系式表示变量之间的关系
3.长方形的长是20,宽是,周长是,面积是 .
(1)写出和 之间的关系式.
【解】由长方形的周长公式,得 .
(2)写出和 之间的关系式.
由长方形的面积公式,得 .
(3)当时,等于多少? 等于多少?
【解】当时,,解得.将 代入
,得 .
(4)当增加1时,增加多少? 增加多少?
当增加1时,.所以当 增加1时,
增加20;当增加1时, ,
所以当增加1时, 增加2.
返回
考点4 用图象表示变量之间的关系
4. 张老师在化学实验室做
实验时,将一杯 的开水放在石棉网上自
然冷却,如图是这杯水冷却时的温度变化图,
根据图中的信息,下列说法不正确的是 ( )
C
A. 水温从逐渐下降到时用了
B. 从开始冷却后时的水温是
C. 实验室的室内温度是
D. 水被自然冷却到了
返回
5. 教材P156素材 如图是某地冬季一天的气温随时间变
化的图象,根据图象回答下列问题:
(1)8时,12时,22时的气温各是多少?
【解】8时,12时,22时的气温分别是,, .
(2)这一天的最高气温是多少?几
时达到的?最低气温呢?
【解】这一天的最高气温是 ,
14时达到的,最低气温是 ,
4时达到的.
(3)这一天的温差是多少?从最低到最高气温经过多长时间?
【解】这一天的温差为,从最低到最高气温经过 .
(4)在什么范围内气温上升?在什么时间范围内气温下降?
【解】在4时时气温上升,在0时时,14时 时气温下降.
(5)图中的点表示什么? 点呢?
点表示8时的气温为;点表示24时的气温为 .
(6)在哪一时刻气温为和 ?
【解】在0时和6时的气温为;在12时和23时的气温为 .
(7)你能预测次日凌晨2时的气温吗?
【解】次日凌晨2时的气温约为 (大致范围).
返回
思想1 数形结合思想
6. 骆驼被称为“沙漠之舟”,它的体
温随时间的变化而发生较大变化,
其体温 与时间(时)之间的关系
D
如图①所示.小清同学根据图①绘制了图②,则图②中的变量
最有可能表示的是 ( )
A. 骆驼在 时刻的体温与0时体温的绝对差(即差的绝对值)
B. 骆驼从0时到 时刻之间的最高体温与当日最低体温的差
C. 骆驼在 时刻的体温与当日平均体温的绝对差
D. 骆驼从0时到 时刻之间的体温最大值与最小值的差
【点拨】从0时到4时,温差随时间
的增大而增大,在4时达到最大,是
;从4时到8时,这段时间的最
高体温是,最低体温是 ,
温差不变,从8时开始,最高体温变大,最低体温不变是
,温差变大,达到 ,从16时开始到24时体温下降,
温差不变.即变量最有可能表示的是骆驼从0时到 时刻之间
的体温最大值与最小值的差.
返回
思想2 分类讨论思想
7.[2024济南期末] 甲、乙两车分别从, 两
地同时出发,甲车匀速前往地,到达 地
后停止;乙车匀速前往地,到达 地立即
以另一速度按原路匀速返回到地,返回到 地时停止.设甲、
乙两车距地的路程为(千米),乙车行驶的时间为
(时),与 之间的图象如图所示.
(1)乙车从地返回 地的速度是_____千米/时;
(2)乙车到达地时甲车距 地的路程是
_____千米;
100
100
(3)求乙车返回前甲、乙两车相距40千米时,乙车行驶的
时间.
【解】由图象易知甲车的速度为80千米/
时,乙车从地到 地的速度为120千米/
时,当乙车返回前甲、乙两车相距40千
米时,
设乙车行驶的时间为 小时,甲、乙两车相遇之前:
,
解得 ;
甲、乙两车相遇之后:
,
解得 .
综上所述,乙车返回前甲、乙两车相距
40千米时,乙车行驶的时间为1.3小时或
1.7小时.
返回
谢谢观看!
◆懂得学习的人不如喜爱学习的人,喜爱学习的人不如以学习为乐的人.
同课章节目录
