沪科版七下(2024版)8.1.2 幂的乘方与积的乘方(1) 课件
文档属性
| 名称 | 沪科版七下(2024版)8.1.2 幂的乘方与积的乘方(1) 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-04 14:07:49 | ||
图片预览






文档简介
(共20张PPT)
第8章 整式乘法与因式分解
8.1.2 幂的乘方与积的乘方(1)
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
经历探索幂的乘方法则的过程,理解幂的乘方法则。
01
掌握幂的乘方法则,并能运用法则进行相关计算。
02
会综合运用同底数幂的乘法法则和幂的乘方法则进行简单的混合运算。
03
体验从特殊到一般、从具体到抽象的思考方法,感受数学推导过程的乐趣。
04
02
新知导入
计算:
(m,n都是正整数),
同底数幂相乘,底数__________,指数_______。
(m,n,,p都是正整数)。
不变
相加
03
新知探究
思考:怎样计算?
算式 运算过程 结果
先填写下列表格:
观察上表,幂的乘方有什么规律?
03
新知探究
==56
==
==
==
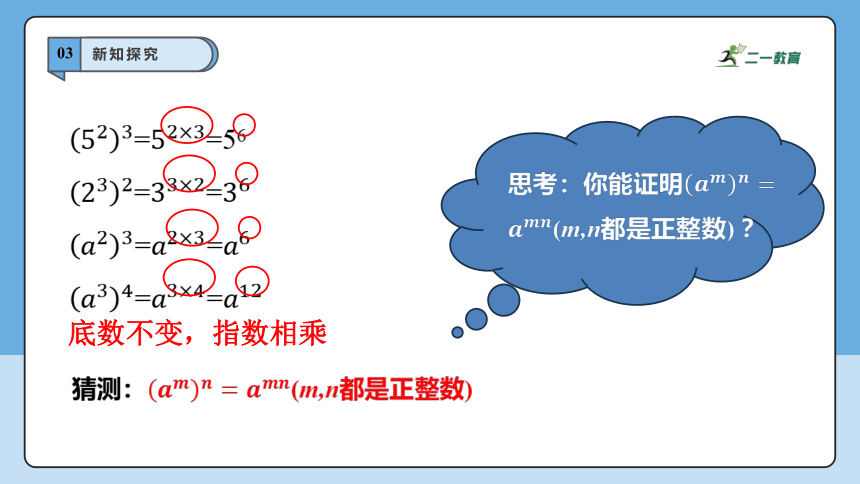
底数不变,指数相乘
猜测:(m,n都是正整数)
思考:你能证明(m,n都是正整数) ?
证明
一般地,如果m,n都是正整数,那么
03
新知探究
幂的运算性质2:
(m,n都是正整数)
幂的乘方,底数不变,指数相乘.
03
新知探究
例2
计算:(1) (105)3; (2) (x4)2.
解:(1)(105)3=105×3= 1015;
(2) (x4)2= x4×2=x8.
03
新知探究
例3
计算:(1) (x3)2+ x2x4; (2) (x2)3 (x4)3.
解:(1)(x3)2+ x2x4 = x3×2+ x2+4 =x6+x6=2x6;
(2) (x2)3 (x4)3 = x2×3 x4×3 =x6 x12 =x6+12= x18.
04
课堂练习
【知识技能类作业】必做题:
1.计算(x3)5的结果是( )
A.x2 B.x8 C.x15 D.x16
2.若k为正整数,则(k3)4的意义为( )
A.4个k3相加 B.3个k4相加 C.4个k3相乘 D.7个k相乘
3.如果(3n)2=316,则n的值为 ( )
A.3 B.4 C.8 D.14
C
C
C
04
课堂练习
【知识技能类作业】选做题:
4.已知am=2,则a3m的值为 .
5.已知a2x=3,则(ax)4的值是 .
6.已知3×9m×27m=321,则m的值为 .
8
9
4
04
课堂练习
【综合拓展类作业】
7.计算:(1)(x4)3+x2·(x5)2; (2)[(a+b)2]m·(a+b);
(3)(x2n-1)2·x2; (4)4(a2)3-2a·a5.
解:(1)原式=x12+x2·x10=x12+x12=2x12.
(2)原式=(a+b)2m·(a+b)=(a+b)2m+1.
(3)原式=x4n-2·x2=x4n.
(4)原式=4×a6-2a6=2a6.
05
课堂小结
幂的运算性质2:
(m,n都是正整数)
幂的乘方,底数不变,指数相乘.
06
作业布置
【知识技能类作业】
1.正方体的棱长是(1-3b)2,则它的体积是 ( )
A.(1-3b)6 B.(1-3b)9 C.(1-3b)12 D.(1-3b)5
2.在下列各式的括号内,应填入b4的是 ( )
A.b12=( )8 B.b12=( )6 C.b12=( )3 D.b12=( )2
3.已知am=3,an=4,求a2m+3n的值。
A
C
解:a2m+3n=a2m·a3n=(am)2·(an)3=32×43=576.
06
作业布置
【综合拓展类作业】
4.(1)已知2x+5y-3=0,求4x·32y的值.
解:(1)因为2x+5y-3=0,
所以2x+5y=3,
所以4x·32y=22x·25y=22x+5y=23=8.
06
作业布置
【综合拓展类作业】
4. (2)已知2×8x×16=223,求x的值.
解 :(2)因为2×8x×16=223,
所以2×23x×24=223,
所以1+3x+4=23,解得x=6.
07
板书设计
幂的运算性质2:
(m,n都是正整数)
幂的乘方,底数不变,指数相乘.
8.1.2 幂的乘方与积的乘方(1)
习题讲解书写部分
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第8章 整式乘法与因式分解
8.1.2 幂的乘方与积的乘方(1)
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
经历探索幂的乘方法则的过程,理解幂的乘方法则。
01
掌握幂的乘方法则,并能运用法则进行相关计算。
02
会综合运用同底数幂的乘法法则和幂的乘方法则进行简单的混合运算。
03
体验从特殊到一般、从具体到抽象的思考方法,感受数学推导过程的乐趣。
04
02
新知导入
计算:
(m,n都是正整数),
同底数幂相乘,底数__________,指数_______。
(m,n,,p都是正整数)。
不变
相加
03
新知探究
思考:怎样计算?
算式 运算过程 结果
先填写下列表格:
观察上表,幂的乘方有什么规律?
03
新知探究
==56
==
==
==
底数不变,指数相乘
猜测:(m,n都是正整数)
思考:你能证明(m,n都是正整数) ?
证明
一般地,如果m,n都是正整数,那么
03
新知探究
幂的运算性质2:
(m,n都是正整数)
幂的乘方,底数不变,指数相乘.
03
新知探究
例2
计算:(1) (105)3; (2) (x4)2.
解:(1)(105)3=105×3= 1015;
(2) (x4)2= x4×2=x8.
03
新知探究
例3
计算:(1) (x3)2+ x2x4; (2) (x2)3 (x4)3.
解:(1)(x3)2+ x2x4 = x3×2+ x2+4 =x6+x6=2x6;
(2) (x2)3 (x4)3 = x2×3 x4×3 =x6 x12 =x6+12= x18.
04
课堂练习
【知识技能类作业】必做题:
1.计算(x3)5的结果是( )
A.x2 B.x8 C.x15 D.x16
2.若k为正整数,则(k3)4的意义为( )
A.4个k3相加 B.3个k4相加 C.4个k3相乘 D.7个k相乘
3.如果(3n)2=316,则n的值为 ( )
A.3 B.4 C.8 D.14
C
C
C
04
课堂练习
【知识技能类作业】选做题:
4.已知am=2,则a3m的值为 .
5.已知a2x=3,则(ax)4的值是 .
6.已知3×9m×27m=321,则m的值为 .
8
9
4
04
课堂练习
【综合拓展类作业】
7.计算:(1)(x4)3+x2·(x5)2; (2)[(a+b)2]m·(a+b);
(3)(x2n-1)2·x2; (4)4(a2)3-2a·a5.
解:(1)原式=x12+x2·x10=x12+x12=2x12.
(2)原式=(a+b)2m·(a+b)=(a+b)2m+1.
(3)原式=x4n-2·x2=x4n.
(4)原式=4×a6-2a6=2a6.
05
课堂小结
幂的运算性质2:
(m,n都是正整数)
幂的乘方,底数不变,指数相乘.
06
作业布置
【知识技能类作业】
1.正方体的棱长是(1-3b)2,则它的体积是 ( )
A.(1-3b)6 B.(1-3b)9 C.(1-3b)12 D.(1-3b)5
2.在下列各式的括号内,应填入b4的是 ( )
A.b12=( )8 B.b12=( )6 C.b12=( )3 D.b12=( )2
3.已知am=3,an=4,求a2m+3n的值。
A
C
解:a2m+3n=a2m·a3n=(am)2·(an)3=32×43=576.
06
作业布置
【综合拓展类作业】
4.(1)已知2x+5y-3=0,求4x·32y的值.
解:(1)因为2x+5y-3=0,
所以2x+5y=3,
所以4x·32y=22x·25y=22x+5y=23=8.
06
作业布置
【综合拓展类作业】
4. (2)已知2×8x×16=223,求x的值.
解 :(2)因为2×8x×16=223,
所以2×23x×24=223,
所以1+3x+4=23,解得x=6.
07
板书设计
幂的运算性质2:
(m,n都是正整数)
幂的乘方,底数不变,指数相乘.
8.1.2 幂的乘方与积的乘方(1)
习题讲解书写部分
Thanks!
https://www.21cnjy.com/recruitment/home/fine
