3.2平面直角坐标系压轴题训练北师大版2024—2025学年八年级上册期末专题复习(无答案)
文档属性
| 名称 | 3.2平面直角坐标系压轴题训练北师大版2024—2025学年八年级上册期末专题复习(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 109.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-04 00:00:00 | ||
图片预览


文档简介
3.2平面直角坐标系压轴题训练北师大版2024—2025学年八年级上册期末专题复习
一、选择题
1.若定义:f(a,b)=(﹣a,b),g(m,n)=(m,﹣n),例如f(1,2)=(﹣1,2),g(﹣4,﹣5)=(﹣4,5),则g[f(2,﹣3)]可以表示为( )
A.(2,﹣3) B.(﹣2,3) C.(2,3) D.(﹣2,﹣3)
2.如图,一个机器人从点O出发,向正西方向走2m到达点A1;再向正北方向走4m到达点A2,再向正东方向走6m到达点A3,再向正南方向走8m到达点A4,再向正西方向走10m到达点A5,…按如此规律走下去,当机器人走到点A2024时,点A2024的坐标为( )
A.(2024,2024) B.(2024,﹣2024)
C.(﹣2026,﹣2024) D.(2026,﹣2026)
3.如图,在平面直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3,…,已知A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).观察每次变换前后的三角形的变化,按照变换规律,则点An的坐标是( )
A.(2n,3) B.(2n﹣1,3) C.(2n+1,0) D.(2n,0)
二、填空题
1.若点P(2﹣a,2a+5)到两坐标轴的距离相等,则a的值为 .
2.已知点P(a,b)到x轴的距离是2,到y轴的距离是5,且|a﹣b|=a﹣b,则P点坐标是 .
3.已知点P的坐标(2﹣a,3a+6),且点P到两坐标轴的距离相等,则点P的坐标是 .
4.已知点A(3a+5,a﹣3)在二、四象限的角平分线上,则a= .
5.已知点A(m,﹣2),B(3,m﹣1),且直线AB∥x轴,则m的值是 .
6.已知AB∥x轴,A点的坐标为(3,2),并且AB=5,则B的坐标为 .
三、解答题
7.在平面直角坐标系中,已知点M(m,2m+3).
(1)若点M在x轴上,求m的值;
(2)若点M在第二象限内,求m的取值范围;
(3)若点M在第一、三象限的角平分线上,求m的值.
8.已知:A(0,1),B(2,0),C(4,3)
(1)在坐标系中描出各点,画出△ABC.
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.
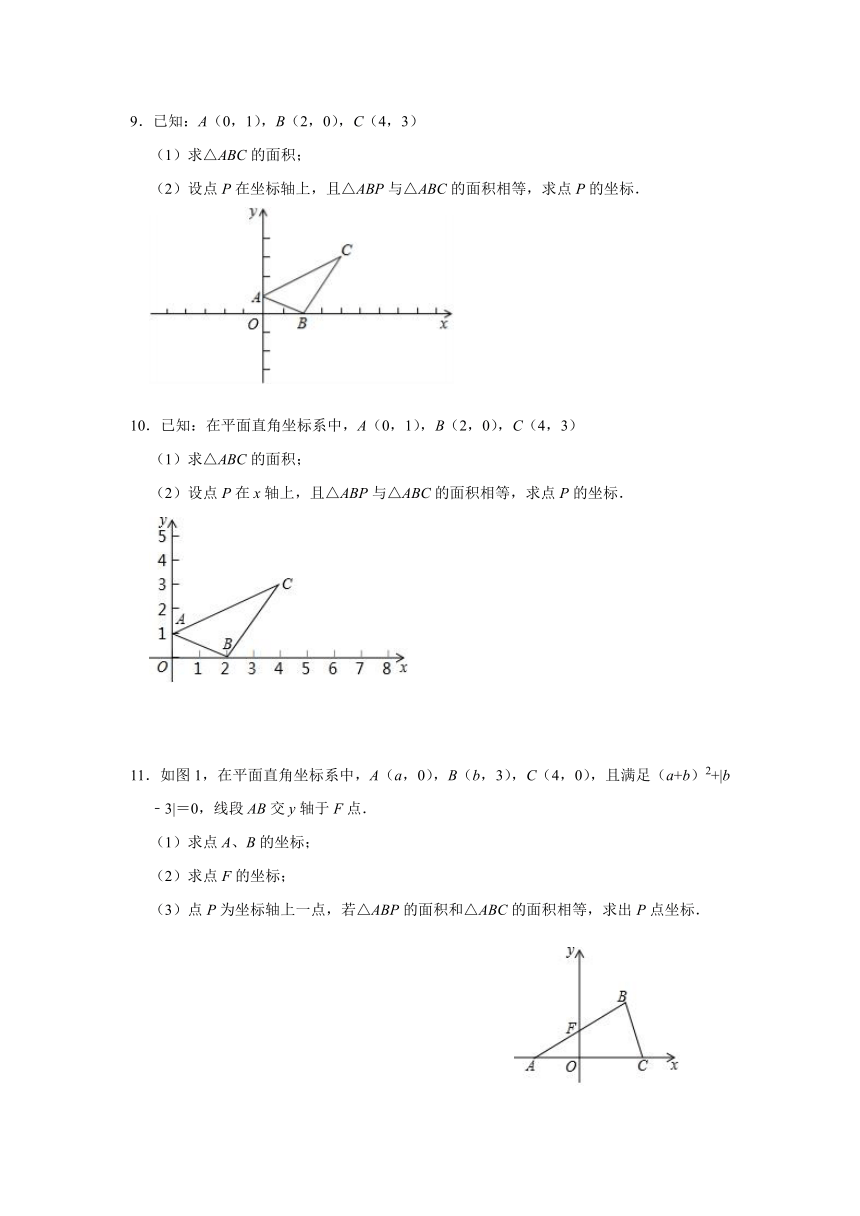
9.已知:A(0,1),B(2,0),C(4,3)
(1)求△ABC的面积;
(2)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.
10.已知:在平面直角坐标系中,A(0,1),B(2,0),C(4,3)
(1)求△ABC的面积;
(2)设点P在x轴上,且△ABP与△ABC的面积相等,求点P的坐标.
11.如图1,在平面直角坐标系中,A(a,0),B(b,3),C(4,0),且满足(a+b)2+|b﹣3|=0,线段AB交y轴于F点.
(1)求点A、B的坐标;
(2)求点F的坐标;
(3)点P为坐标轴上一点,若△ABP的面积和△ABC的面积相等,求出P点坐标.
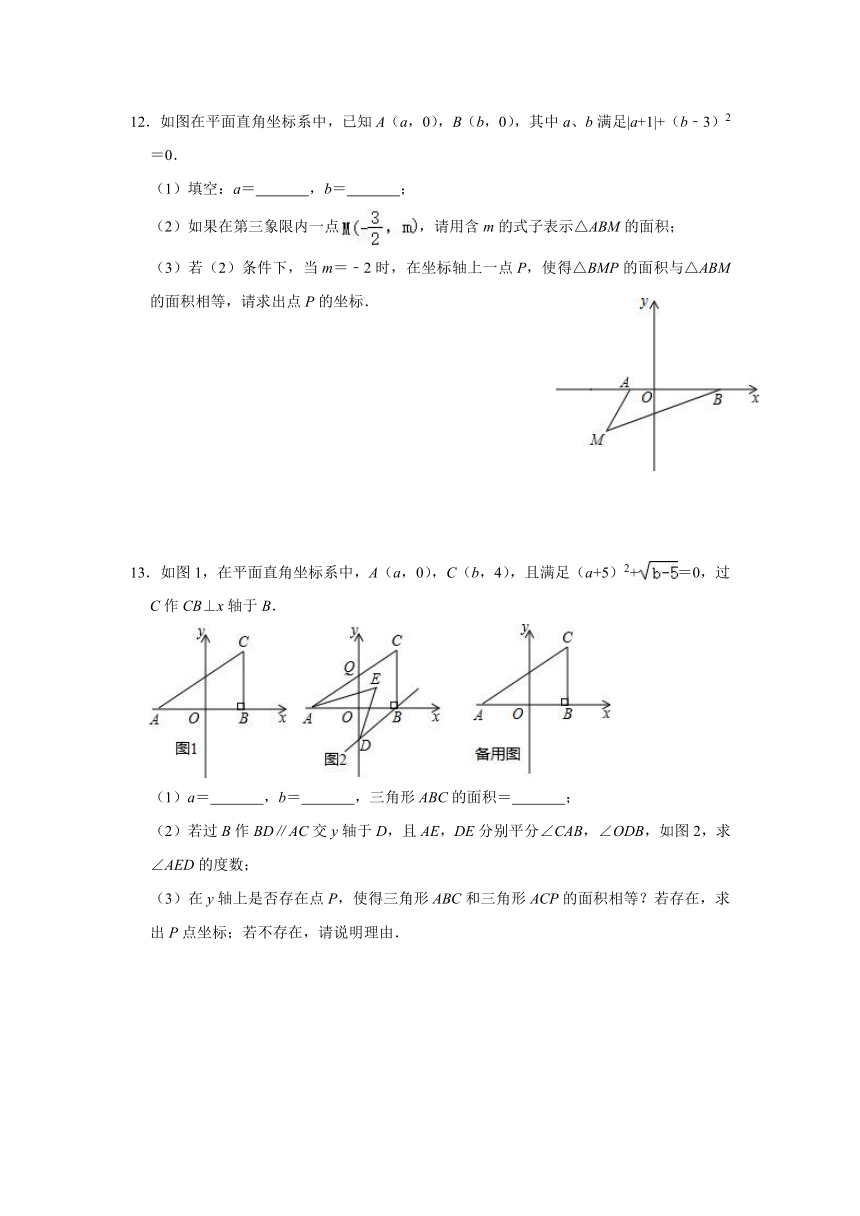
12.如图在平面直角坐标系中,已知A(a,0),B(b,0),其中a、b满足|a+1|+(b﹣3)2=0.
(1)填空:a= ,b= ;
(2)如果在第三象限内一点,请用含m的式子表示△ABM的面积;
(3)若(2)条件下,当m=﹣2时,在坐标轴上一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
13.如图1,在平面直角坐标系中,A(a,0),C(b,4),且满足(a+5)2+=0,过C作CB⊥x轴于B.
(1)a= ,b= ,三角形ABC的面积= ;
(2)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图2,求∠AED的度数;
(3)在y轴上是否存在点P,使得三角形ABC和三角形ACP的面积相等?若存在,求出P点坐标;若不存在,请说明理由.
14.如图,已知点A(a,0)、B(b,0)满足(3a+b)2+|b﹣3|=0.将线段AB先向上平移2个单位,再向右平移1个单位后得到线段CD,并连接AC、BD.
(1)请求出点A和点B的坐标;
(2)点M从O点出发,以每秒1个单位的速度向上平移运动.设运动时间为t秒,问:是否存在这样的t,使得四边形OMDB的面积等于8?若存在,请求出t的值;若不存在,请说明理由;
(3)在(2)的条件下,点M从O点出发的同时,点N从点B出发,以每秒2个单位的速度向左平移运动,设射线DN交y轴于点E.设运动时间为t秒,问:S△EMD﹣S△OEN的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.
15.在平面直角坐标系中,O为坐标原点,过点A(8,6)分别作x轴、y轴的平行线,交y轴于点B,交x轴于点C,点P是从点B出发,沿B→A→C以2个单位长度/秒的速度向终点C运动的一个动点,运动时间为t(秒).
(1)直接写出点B和点C的坐标B( , )、C( , );
(2)当点P运动时,用含t的式子表示线段AP的长,并写出t的取值范围;
(3)点D(2,0),连接PD、AD,在(2)条件下是否存在这样的t值,使S△APD=S四边形ABOC,若存在,请求出t值,若不存在,请说明理由.
16.如图,在平面直角坐标系中,四边形ABCD为长方形,其中点A、C坐标分别为(﹣4,2)、(1,﹣4),且AD∥x轴,交y轴于M点,AB交x轴于N.
(1)直接写出B、D两点坐标,并求出长方形ABCD的面积;
(2)一动点P从A出发,以每秒个单位长度的速度沿AB边向B点运动,在P点运动过程中,连接MP、OP,试探究∠AMP、∠MPO、∠PON之间的数量关系;(写出你的探究过程以及结论)
(3)在(2)的条件下,是否存在某一时刻t,使得三角形AMP的面积等于长方形ABCD面积的?若存在,求t的值以及此时点P的坐标;若不存在说明理由.
17.在平面直角坐标系中,有点A(﹣2,a+3),B(b,b﹣3).
(1)当点A在第二象限的角平分线上时,求a的值;
(2)当点B到x轴的距离是它到y轴的距离2倍时,求点B所在的象限位置.
18.已知点P(a﹣2,2a+8),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点Q的坐标为(1,5),直线PQ∥y轴;
(3)点P到x轴、y轴的距离相等.
19.问题情境:
在平面直角坐标系xOy中有不重合的两点A(x1,y1)和点B(x2,y2),小明在学习中发现,若x1=x2,则AB∥y轴,且线段AB的长度为|y1﹣y2|;若y1=y2,则AB∥x轴,且线段AB的长度为|x1﹣x2|;
【应用】:
(1)若点A(﹣1,1)、B(2,1),则AB∥x轴,AB的长度为 .
(2)若点C(1,0),且CD∥y轴,且CD=2,则点D的坐标为 .
【拓展】:
我们规定:平面直角坐标系中任意不重合的两点M(x1,y1),N(x2,y2)之间的折线距离为d(M,N)=|x1﹣x2|+|y1﹣y2|;例如:图1中,点M(﹣1,1)与点N(1,﹣2)之间的折线距离为d(M,N)=|﹣1﹣1|+|1﹣(﹣2)|=2+3=5.
解决下列问题:
(1)如图1,已知E(2,0),若F(﹣1,﹣2),则d(E,F) ;
(2)如图2,已知E(2,0),H(1,t),若d(E,H)=3,则t= .
(3)如图3,已知P(3,3),点Q在x轴上,且三角形OPQ的面积为3,则d(P,Q)= .
一、选择题
1.若定义:f(a,b)=(﹣a,b),g(m,n)=(m,﹣n),例如f(1,2)=(﹣1,2),g(﹣4,﹣5)=(﹣4,5),则g[f(2,﹣3)]可以表示为( )
A.(2,﹣3) B.(﹣2,3) C.(2,3) D.(﹣2,﹣3)
2.如图,一个机器人从点O出发,向正西方向走2m到达点A1;再向正北方向走4m到达点A2,再向正东方向走6m到达点A3,再向正南方向走8m到达点A4,再向正西方向走10m到达点A5,…按如此规律走下去,当机器人走到点A2024时,点A2024的坐标为( )
A.(2024,2024) B.(2024,﹣2024)
C.(﹣2026,﹣2024) D.(2026,﹣2026)
3.如图,在平面直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3,…,已知A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).观察每次变换前后的三角形的变化,按照变换规律,则点An的坐标是( )
A.(2n,3) B.(2n﹣1,3) C.(2n+1,0) D.(2n,0)
二、填空题
1.若点P(2﹣a,2a+5)到两坐标轴的距离相等,则a的值为 .
2.已知点P(a,b)到x轴的距离是2,到y轴的距离是5,且|a﹣b|=a﹣b,则P点坐标是 .
3.已知点P的坐标(2﹣a,3a+6),且点P到两坐标轴的距离相等,则点P的坐标是 .
4.已知点A(3a+5,a﹣3)在二、四象限的角平分线上,则a= .
5.已知点A(m,﹣2),B(3,m﹣1),且直线AB∥x轴,则m的值是 .
6.已知AB∥x轴,A点的坐标为(3,2),并且AB=5,则B的坐标为 .
三、解答题
7.在平面直角坐标系中,已知点M(m,2m+3).
(1)若点M在x轴上,求m的值;
(2)若点M在第二象限内,求m的取值范围;
(3)若点M在第一、三象限的角平分线上,求m的值.
8.已知:A(0,1),B(2,0),C(4,3)
(1)在坐标系中描出各点,画出△ABC.
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.
9.已知:A(0,1),B(2,0),C(4,3)
(1)求△ABC的面积;
(2)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.
10.已知:在平面直角坐标系中,A(0,1),B(2,0),C(4,3)
(1)求△ABC的面积;
(2)设点P在x轴上,且△ABP与△ABC的面积相等,求点P的坐标.
11.如图1,在平面直角坐标系中,A(a,0),B(b,3),C(4,0),且满足(a+b)2+|b﹣3|=0,线段AB交y轴于F点.
(1)求点A、B的坐标;
(2)求点F的坐标;
(3)点P为坐标轴上一点,若△ABP的面积和△ABC的面积相等,求出P点坐标.
12.如图在平面直角坐标系中,已知A(a,0),B(b,0),其中a、b满足|a+1|+(b﹣3)2=0.
(1)填空:a= ,b= ;
(2)如果在第三象限内一点,请用含m的式子表示△ABM的面积;
(3)若(2)条件下,当m=﹣2时,在坐标轴上一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
13.如图1,在平面直角坐标系中,A(a,0),C(b,4),且满足(a+5)2+=0,过C作CB⊥x轴于B.
(1)a= ,b= ,三角形ABC的面积= ;
(2)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图2,求∠AED的度数;
(3)在y轴上是否存在点P,使得三角形ABC和三角形ACP的面积相等?若存在,求出P点坐标;若不存在,请说明理由.
14.如图,已知点A(a,0)、B(b,0)满足(3a+b)2+|b﹣3|=0.将线段AB先向上平移2个单位,再向右平移1个单位后得到线段CD,并连接AC、BD.
(1)请求出点A和点B的坐标;
(2)点M从O点出发,以每秒1个单位的速度向上平移运动.设运动时间为t秒,问:是否存在这样的t,使得四边形OMDB的面积等于8?若存在,请求出t的值;若不存在,请说明理由;
(3)在(2)的条件下,点M从O点出发的同时,点N从点B出发,以每秒2个单位的速度向左平移运动,设射线DN交y轴于点E.设运动时间为t秒,问:S△EMD﹣S△OEN的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.
15.在平面直角坐标系中,O为坐标原点,过点A(8,6)分别作x轴、y轴的平行线,交y轴于点B,交x轴于点C,点P是从点B出发,沿B→A→C以2个单位长度/秒的速度向终点C运动的一个动点,运动时间为t(秒).
(1)直接写出点B和点C的坐标B( , )、C( , );
(2)当点P运动时,用含t的式子表示线段AP的长,并写出t的取值范围;
(3)点D(2,0),连接PD、AD,在(2)条件下是否存在这样的t值,使S△APD=S四边形ABOC,若存在,请求出t值,若不存在,请说明理由.
16.如图,在平面直角坐标系中,四边形ABCD为长方形,其中点A、C坐标分别为(﹣4,2)、(1,﹣4),且AD∥x轴,交y轴于M点,AB交x轴于N.
(1)直接写出B、D两点坐标,并求出长方形ABCD的面积;
(2)一动点P从A出发,以每秒个单位长度的速度沿AB边向B点运动,在P点运动过程中,连接MP、OP,试探究∠AMP、∠MPO、∠PON之间的数量关系;(写出你的探究过程以及结论)
(3)在(2)的条件下,是否存在某一时刻t,使得三角形AMP的面积等于长方形ABCD面积的?若存在,求t的值以及此时点P的坐标;若不存在说明理由.
17.在平面直角坐标系中,有点A(﹣2,a+3),B(b,b﹣3).
(1)当点A在第二象限的角平分线上时,求a的值;
(2)当点B到x轴的距离是它到y轴的距离2倍时,求点B所在的象限位置.
18.已知点P(a﹣2,2a+8),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点Q的坐标为(1,5),直线PQ∥y轴;
(3)点P到x轴、y轴的距离相等.
19.问题情境:
在平面直角坐标系xOy中有不重合的两点A(x1,y1)和点B(x2,y2),小明在学习中发现,若x1=x2,则AB∥y轴,且线段AB的长度为|y1﹣y2|;若y1=y2,则AB∥x轴,且线段AB的长度为|x1﹣x2|;
【应用】:
(1)若点A(﹣1,1)、B(2,1),则AB∥x轴,AB的长度为 .
(2)若点C(1,0),且CD∥y轴,且CD=2,则点D的坐标为 .
【拓展】:
我们规定:平面直角坐标系中任意不重合的两点M(x1,y1),N(x2,y2)之间的折线距离为d(M,N)=|x1﹣x2|+|y1﹣y2|;例如:图1中,点M(﹣1,1)与点N(1,﹣2)之间的折线距离为d(M,N)=|﹣1﹣1|+|1﹣(﹣2)|=2+3=5.
解决下列问题:
(1)如图1,已知E(2,0),若F(﹣1,﹣2),则d(E,F) ;
(2)如图2,已知E(2,0),H(1,t),若d(E,H)=3,则t= .
(3)如图3,已知P(3,3),点Q在x轴上,且三角形OPQ的面积为3,则d(P,Q)= .
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
