3.1圆柱的表面积课件(共21张PPT)2024-2025学年六年级下册数学人教版
文档属性
| 名称 | 3.1圆柱的表面积课件(共21张PPT)2024-2025学年六年级下册数学人教版 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-04 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
第三单元 圆柱和圆锥
圆柱的表面积
教学新知
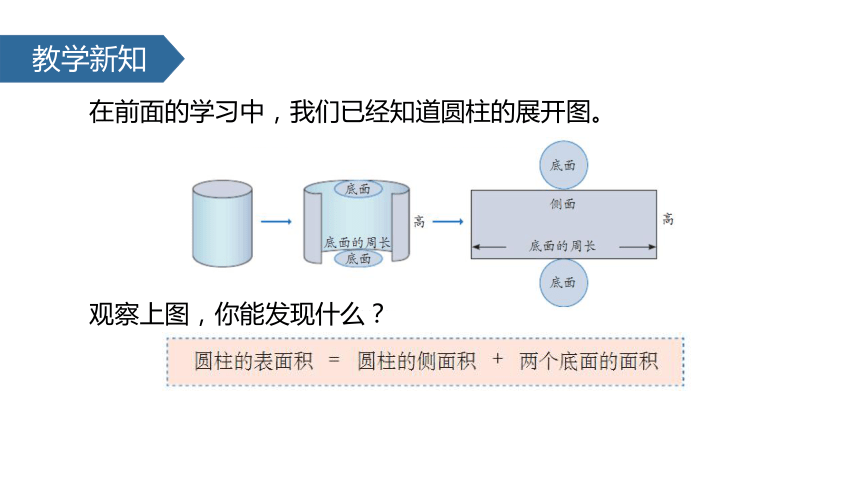
在前面的学习中,我们已经知道圆柱的展开图。
观察上图,你能发现什么?
教学新知
讨论:如果我们知道了圆柱的底面半径或直径,以及高的数据,很容易
就能得出两个圆形的面积,那怎样求侧面的面积呢?请同学们小
组交流一下方法,然后再全班交流。
把圆柱的侧面转化为平面图形,圆柱的侧面展开后不论是长方形、正方形或平行四边形,圆柱的侧面积都等于它的底面周长乘高。
圆柱侧面积=底面周长×高
教学新知
做一做:一个圆柱形茶叶桶的侧面贴着商标纸,圆柱底面半径是5 cm,
高是20 cm。这张商标纸的面积是多少?
请你说说如何根据直径或半径以及高的数据计算圆柱体的侧面积?
2×3.14×5×20=628(cm )
答:这张商标纸的面积是628cm
教学新知
试一试:一顶圆柱形厨师帽,高30 cm,帽顶直径20 cm,做这样一顶
帽子至少要用多少平方厘米的面料?(得数保留整十数。)
想一想:在解决这个问题时要注意什么?
教学新知
①侧面积:3.14×20×30=1884(平方厘米)
②底面积:3.14×(20÷2) =314(平方厘米)
③表面积:1884+314=2198≈2200(平方厘米)
这道题使用的材料要比计算得到的结果多一些。因此,这里不能用四舍五入法取近似值,不管省略的数值比4大还是比4小,都要向前一位进1,解决这类问题往往用“进一法”取近似数。
教学新知
做一做:求下面各圆柱的侧面积。
(1)底面周长是1.6 m,高是0.7 m。
(2)底面半径是3.2 dm,高5 dm。小亚做了一个笔筒,她想给笔筒
的侧面和底面贴上彩纸,至少需要用多少 彩纸?
1.6×0.7=1.12(m )
2×3.14×3.2×5=100.48(dm )
教学新知
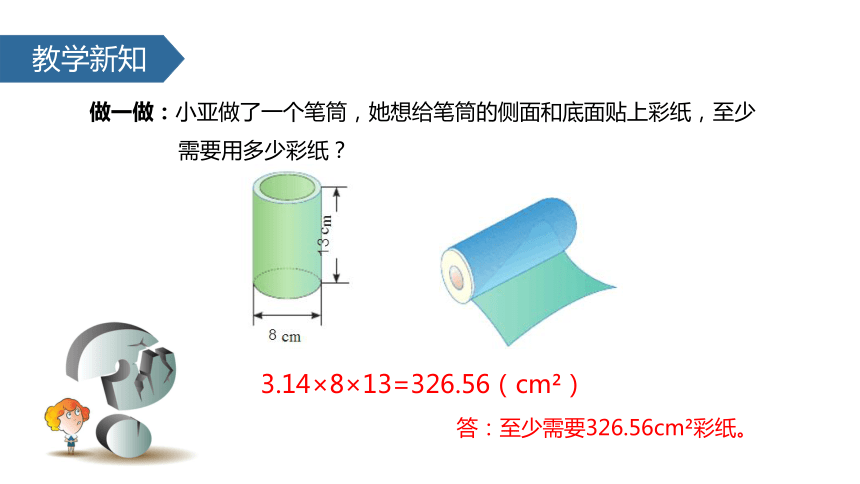
做一做:小亚做了一个笔筒,她想给笔筒的侧面和底面贴上彩纸,至少
需要用多少彩纸?
3.14×8×13=326.56(cm )
答:至少需要326.56cm 彩纸。
教学新知
练一练:
1.广告公司制作了一个底面直径是1.5 m、高2.5 m的圆柱 形灯箱。可
以张贴多大面积的海报?
2.修建一个圆柱形的沼气池,底面直径是3 m,深2 m。在 池的四壁与
下底面抹上水泥,抹水泥部分的面积是多少平方米?
3.14×1.5×2.5=11.775(平方米)
答:可以张贴11.77555平方米的海报。
3.14×(3÷2) +3.14×3×2=25.905(平方米)
答:抹水泥部分的面积是25.905平方米。
教学新知
3.某种饮料罐的形状为圆柱形,底面直径为6 cm, 高为12 cm,将24罐
这种饮料按如图所示的方式放入箱内,这个箱子的长、宽、高至少是多
少厘米?
长为6×6=36(cm)
宽为6×4=24(cm)
高为12cm
知识要点
圆柱的表面积=圆柱的侧面积+底面积×2
圆柱的侧面积=底面周长×高
教学新知
例一:一个圆柱体的底面直径是6厘米,高是5厘米,这个圆柱体的侧面
积是多少?
【解析】圆柱体的侧面积等于底面周长乘高,题中告诉了底面直径,根据直径我们可以求底面周长,然后就能求出圆柱体的侧面积了,列式计算为:3.14×6×5=94.2(平方厘米)。
【方法小结】求圆柱体的侧面积要根据题中的已知条件求出底面周长,然后再按要求进行计算。
教学新知
例二:一个易拉罐高8厘米,底面半径为3厘米,这个易拉罐的表面积是
多少?
【讲解】可以用分步计算的方法去求,列式计算为:底面积=3.14×3 ×2=56.52(平方厘米);
侧面积=2×3.14×3×8=150.72(平方厘米);
表面积=56.52+150.72=207.24(平方厘米)。
【方法小结】求圆柱体的表面积要分别计算出底面积和侧面积,然后再把它们加起来,当然方法熟练以后也可列综合算式,但一定要细心计算。
教学新知
例三:要给一个饼干桶的四周贴上商标纸,如果饼干桶的底面半径是4
厘米,高为20厘米,要贴的商标纸的面积是多少平方厘米?
【讲解】这也是一道求表面积的习题,但是又有其特殊性,给饼干桶贴商标,上下两底是不用贴的,所以求得的面积其实就是侧面的面积,所以列式计算为:2×3.14×4×20=502.4(平方厘米)。
【方法小结】求特殊的圆柱体表面积要对圆柱体进行分析,到底是求几个底面的面积,然后按题中的条件认真计算。
课堂练习
1.请你拿出自己准备的露露瓶,先量出它的底面直径或半径以及高的数值, 然后再分别计算这个露露瓶的侧面积和表面积。
2.砌一个圆柱形沼气池,底面直径是4米,深是2米。在池的周围与底面
抹上水泥,抹水泥部分的面积是多少平方米?
3.14×(4÷2) +3.14×4×2=37.68(平方米)
答:抹水泥部分的面积是37.68平方米。
课堂练习
3.一个圆柱形蓄水池,直径10米,深2米。这个蓄水池的占地面积是多少
在池的一周及池底抹上水泥,抹水泥的面积是多少?
4.一个圆柱体的侧面积是226.08平方厘米,底面半径4厘米,它的高是
多少?
3.14×(10÷2) =78.5(米 )
答:抹水泥的面积是78.5平方米。
2×3.14×4=25.12(厘米) 226.08÷25.12=9(厘米)
答:它的高是9cm。
课堂练习
5.把一棱长10厘米的正方形木块,削成一个最大的圆柱体,这个圆柱体的
表面积是多少?
6.一个没有盖的圆柱形铁皮水桶,高是24厘米,底面直径是20厘米,做
这个水桶要用铁皮多少平方厘米?(得数保留整百平方厘米)
2×3.14×(10÷2) +3.14×10×10=471(平方厘米) 答:这个圆柱的表面积是471平方厘米。
3.14×(20÷2) +3.14×20×24=1821.2≈1900(平方厘米)
答:约用铁皮1900平方厘米。
课后习题
1.计算下面各圆柱的表面积。
(1)C=6.28厘米,h=8厘米
6.28÷2÷3.14=1(厘米)
6.28×8+3.14×1 ×2=56.52(平方厘米)
(2)d=6米,h=3米
3.14×6×3+3.14×(6÷2) ×2=113.04(平方米)
(3)r=2分米,h=6分米
2×3.14×2×6+3.14×2 ×2=100.48(平方分米)
课后习题
2.填空。
(1)用一张长5厘米、宽8厘米的长方形纸围成一个圆柱体,这个圆柱体
的侧面积是( )平方厘米。
(2)做一节底面直径是10厘米、长95厘米的圆柱体通风管,至少用一张
长( )厘米宽( )厘米的长方形铁皮。
3.一个圆柱,底面周长是94.5厘米,高是25厘米,求它的侧面积。
94.5×25=2362.5(平方厘米)
答:它的侧面积是2362.5平方厘米。
40
95
31.4
课后习题
4.一个圆柱,底面直径是2分米,高是45分米,求它的表面积。
5.一个没有盖的圆柱形水桶,底面直径是4分米,高是8分米,要在水桶
的里、外面都涂上防锈漆,油漆的面积大约是多少平方分米?(得数
保留整数。)
3.14×2×45+3.14×(2÷2) ×2=288.88(平方分米)
答:它的表面积是288.88平方分米。
3.14×(4÷2) +3.14×4×8=113.04(平方分米)
113.04×2=226.08≈227(平方分米)
答:油漆的面积大约是227平方分米。
课后习题
6.把一个圆柱体的侧面展开,得到一个边长6.28分米的正方形,这个圆柱
体的底面周长是多少分米?底面积是多少平方分米?
7.压路机的滚筒是圆柱体,它的长是2米,滚筒横截面的半径是0.6米。
如果每分转动5周,每分可以压多大的路面?
6.28÷3.14÷2=1(分米) 3.14×1 =3.14(平方分米)
答:底面周长是6.28分米,底面积是3.14平方分米。
2×3.14×0.6×2×5=37.68(平方米)
答:每分钟可以压37.68平方米的路面。
第三单元 圆柱和圆锥
圆柱的表面积
教学新知
在前面的学习中,我们已经知道圆柱的展开图。
观察上图,你能发现什么?
教学新知
讨论:如果我们知道了圆柱的底面半径或直径,以及高的数据,很容易
就能得出两个圆形的面积,那怎样求侧面的面积呢?请同学们小
组交流一下方法,然后再全班交流。
把圆柱的侧面转化为平面图形,圆柱的侧面展开后不论是长方形、正方形或平行四边形,圆柱的侧面积都等于它的底面周长乘高。
圆柱侧面积=底面周长×高
教学新知
做一做:一个圆柱形茶叶桶的侧面贴着商标纸,圆柱底面半径是5 cm,
高是20 cm。这张商标纸的面积是多少?
请你说说如何根据直径或半径以及高的数据计算圆柱体的侧面积?
2×3.14×5×20=628(cm )
答:这张商标纸的面积是628cm
教学新知
试一试:一顶圆柱形厨师帽,高30 cm,帽顶直径20 cm,做这样一顶
帽子至少要用多少平方厘米的面料?(得数保留整十数。)
想一想:在解决这个问题时要注意什么?
教学新知
①侧面积:3.14×20×30=1884(平方厘米)
②底面积:3.14×(20÷2) =314(平方厘米)
③表面积:1884+314=2198≈2200(平方厘米)
这道题使用的材料要比计算得到的结果多一些。因此,这里不能用四舍五入法取近似值,不管省略的数值比4大还是比4小,都要向前一位进1,解决这类问题往往用“进一法”取近似数。
教学新知
做一做:求下面各圆柱的侧面积。
(1)底面周长是1.6 m,高是0.7 m。
(2)底面半径是3.2 dm,高5 dm。小亚做了一个笔筒,她想给笔筒
的侧面和底面贴上彩纸,至少需要用多少 彩纸?
1.6×0.7=1.12(m )
2×3.14×3.2×5=100.48(dm )
教学新知
做一做:小亚做了一个笔筒,她想给笔筒的侧面和底面贴上彩纸,至少
需要用多少彩纸?
3.14×8×13=326.56(cm )
答:至少需要326.56cm 彩纸。
教学新知
练一练:
1.广告公司制作了一个底面直径是1.5 m、高2.5 m的圆柱 形灯箱。可
以张贴多大面积的海报?
2.修建一个圆柱形的沼气池,底面直径是3 m,深2 m。在 池的四壁与
下底面抹上水泥,抹水泥部分的面积是多少平方米?
3.14×1.5×2.5=11.775(平方米)
答:可以张贴11.77555平方米的海报。
3.14×(3÷2) +3.14×3×2=25.905(平方米)
答:抹水泥部分的面积是25.905平方米。
教学新知
3.某种饮料罐的形状为圆柱形,底面直径为6 cm, 高为12 cm,将24罐
这种饮料按如图所示的方式放入箱内,这个箱子的长、宽、高至少是多
少厘米?
长为6×6=36(cm)
宽为6×4=24(cm)
高为12cm
知识要点
圆柱的表面积=圆柱的侧面积+底面积×2
圆柱的侧面积=底面周长×高
教学新知
例一:一个圆柱体的底面直径是6厘米,高是5厘米,这个圆柱体的侧面
积是多少?
【解析】圆柱体的侧面积等于底面周长乘高,题中告诉了底面直径,根据直径我们可以求底面周长,然后就能求出圆柱体的侧面积了,列式计算为:3.14×6×5=94.2(平方厘米)。
【方法小结】求圆柱体的侧面积要根据题中的已知条件求出底面周长,然后再按要求进行计算。
教学新知
例二:一个易拉罐高8厘米,底面半径为3厘米,这个易拉罐的表面积是
多少?
【讲解】可以用分步计算的方法去求,列式计算为:底面积=3.14×3 ×2=56.52(平方厘米);
侧面积=2×3.14×3×8=150.72(平方厘米);
表面积=56.52+150.72=207.24(平方厘米)。
【方法小结】求圆柱体的表面积要分别计算出底面积和侧面积,然后再把它们加起来,当然方法熟练以后也可列综合算式,但一定要细心计算。
教学新知
例三:要给一个饼干桶的四周贴上商标纸,如果饼干桶的底面半径是4
厘米,高为20厘米,要贴的商标纸的面积是多少平方厘米?
【讲解】这也是一道求表面积的习题,但是又有其特殊性,给饼干桶贴商标,上下两底是不用贴的,所以求得的面积其实就是侧面的面积,所以列式计算为:2×3.14×4×20=502.4(平方厘米)。
【方法小结】求特殊的圆柱体表面积要对圆柱体进行分析,到底是求几个底面的面积,然后按题中的条件认真计算。
课堂练习
1.请你拿出自己准备的露露瓶,先量出它的底面直径或半径以及高的数值, 然后再分别计算这个露露瓶的侧面积和表面积。
2.砌一个圆柱形沼气池,底面直径是4米,深是2米。在池的周围与底面
抹上水泥,抹水泥部分的面积是多少平方米?
3.14×(4÷2) +3.14×4×2=37.68(平方米)
答:抹水泥部分的面积是37.68平方米。
课堂练习
3.一个圆柱形蓄水池,直径10米,深2米。这个蓄水池的占地面积是多少
在池的一周及池底抹上水泥,抹水泥的面积是多少?
4.一个圆柱体的侧面积是226.08平方厘米,底面半径4厘米,它的高是
多少?
3.14×(10÷2) =78.5(米 )
答:抹水泥的面积是78.5平方米。
2×3.14×4=25.12(厘米) 226.08÷25.12=9(厘米)
答:它的高是9cm。
课堂练习
5.把一棱长10厘米的正方形木块,削成一个最大的圆柱体,这个圆柱体的
表面积是多少?
6.一个没有盖的圆柱形铁皮水桶,高是24厘米,底面直径是20厘米,做
这个水桶要用铁皮多少平方厘米?(得数保留整百平方厘米)
2×3.14×(10÷2) +3.14×10×10=471(平方厘米) 答:这个圆柱的表面积是471平方厘米。
3.14×(20÷2) +3.14×20×24=1821.2≈1900(平方厘米)
答:约用铁皮1900平方厘米。
课后习题
1.计算下面各圆柱的表面积。
(1)C=6.28厘米,h=8厘米
6.28÷2÷3.14=1(厘米)
6.28×8+3.14×1 ×2=56.52(平方厘米)
(2)d=6米,h=3米
3.14×6×3+3.14×(6÷2) ×2=113.04(平方米)
(3)r=2分米,h=6分米
2×3.14×2×6+3.14×2 ×2=100.48(平方分米)
课后习题
2.填空。
(1)用一张长5厘米、宽8厘米的长方形纸围成一个圆柱体,这个圆柱体
的侧面积是( )平方厘米。
(2)做一节底面直径是10厘米、长95厘米的圆柱体通风管,至少用一张
长( )厘米宽( )厘米的长方形铁皮。
3.一个圆柱,底面周长是94.5厘米,高是25厘米,求它的侧面积。
94.5×25=2362.5(平方厘米)
答:它的侧面积是2362.5平方厘米。
40
95
31.4
课后习题
4.一个圆柱,底面直径是2分米,高是45分米,求它的表面积。
5.一个没有盖的圆柱形水桶,底面直径是4分米,高是8分米,要在水桶
的里、外面都涂上防锈漆,油漆的面积大约是多少平方分米?(得数
保留整数。)
3.14×2×45+3.14×(2÷2) ×2=288.88(平方分米)
答:它的表面积是288.88平方分米。
3.14×(4÷2) +3.14×4×8=113.04(平方分米)
113.04×2=226.08≈227(平方分米)
答:油漆的面积大约是227平方分米。
课后习题
6.把一个圆柱体的侧面展开,得到一个边长6.28分米的正方形,这个圆柱
体的底面周长是多少分米?底面积是多少平方分米?
7.压路机的滚筒是圆柱体,它的长是2米,滚筒横截面的半径是0.6米。
如果每分转动5周,每分可以压多大的路面?
6.28÷3.14÷2=1(分米) 3.14×1 =3.14(平方分米)
答:底面周长是6.28分米,底面积是3.14平方分米。
2×3.14×0.6×2×5=37.68(平方米)
答:每分钟可以压37.68平方米的路面。
