24.1.2垂直于弦的直径知识梳理与同步练习人教版2024—2025学年九年级上册(无答案)
文档属性
| 名称 | 24.1.2垂直于弦的直径知识梳理与同步练习人教版2024—2025学年九年级上册(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 660.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-04 21:57:24 | ||
图片预览

文档简介
24.1.2垂直于弦的直径知识梳理与同步练习人教版2024—2025学年九年级上册
一、知识梳理
(一)垂径定理及其推论
问题:如图,AB是⊙O的一条弦,直径CD⊥AB, 垂足为E. 图中相等的线段和劣弧有哪些 为什么
归纳总结:
垂径定理: .
数学语言: .
想一想:下列图形是否具备垂径定理的条件?如果不是,请说明为什么?
归纳总结:
垂径定理的几个基本图形:
思考探索:
(1)如果把垂径定理(垂直于弦的直径平分弦,并且平分弦所对的两条弧)结论与题设交换一条,命题是真命题吗?
(2) 以下五个条件中:①过圆心;②垂直于弦;③平分弦;④平分弦所对的优弧;⑤平分弦所对的劣弧. 任何两个条件都可以推出其他三个结论吗?任选一种组合证明你的猜想.
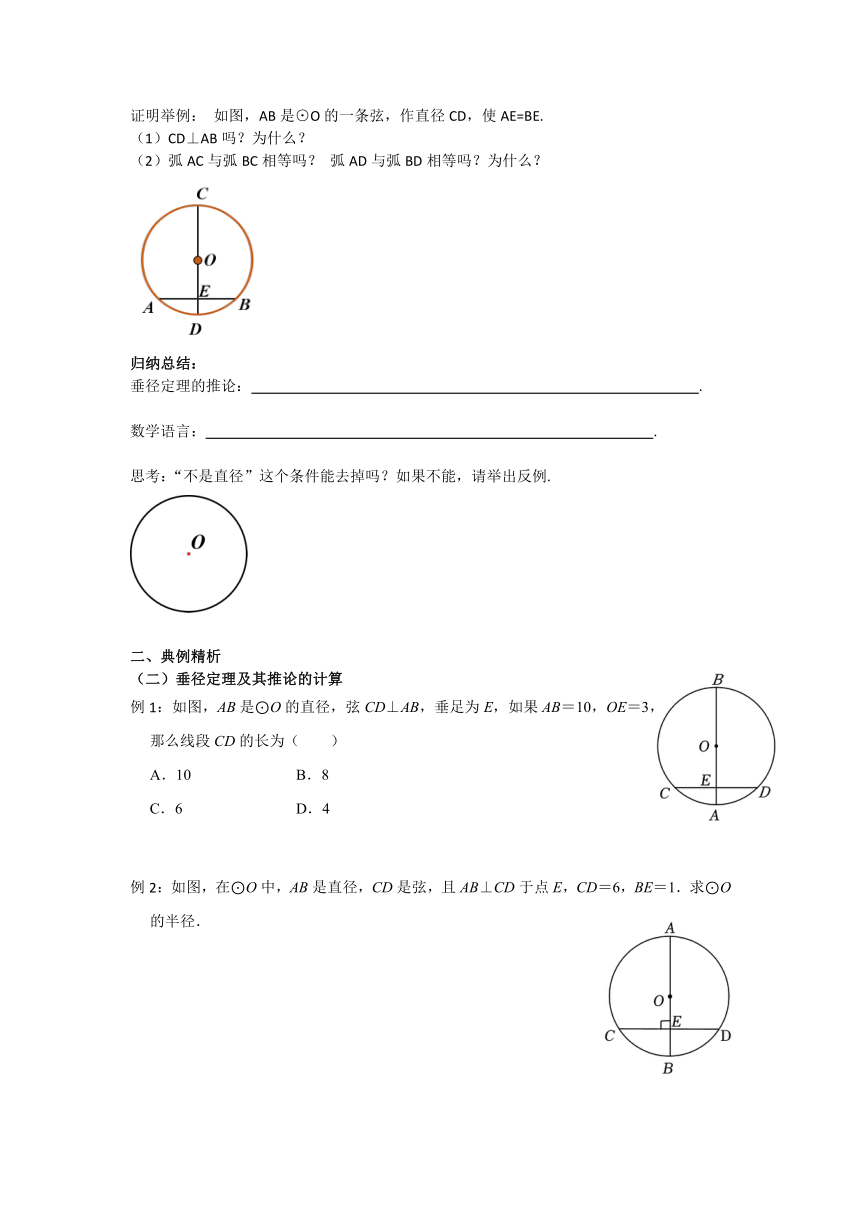
证明举例: 如图,AB是⊙O的一条弦,作直径CD,使AE=BE.
(1)CD⊥AB吗?为什么?
(2)弧AC与弧BC相等吗? 弧AD与弧BD相等吗?为什么?
归纳总结:
垂径定理的推论: .
数学语言: .
思考:“不是直径”这个条件能去掉吗?如果不能,请举出反例.
二、典例精析
(二)垂径定理及其推论的计算
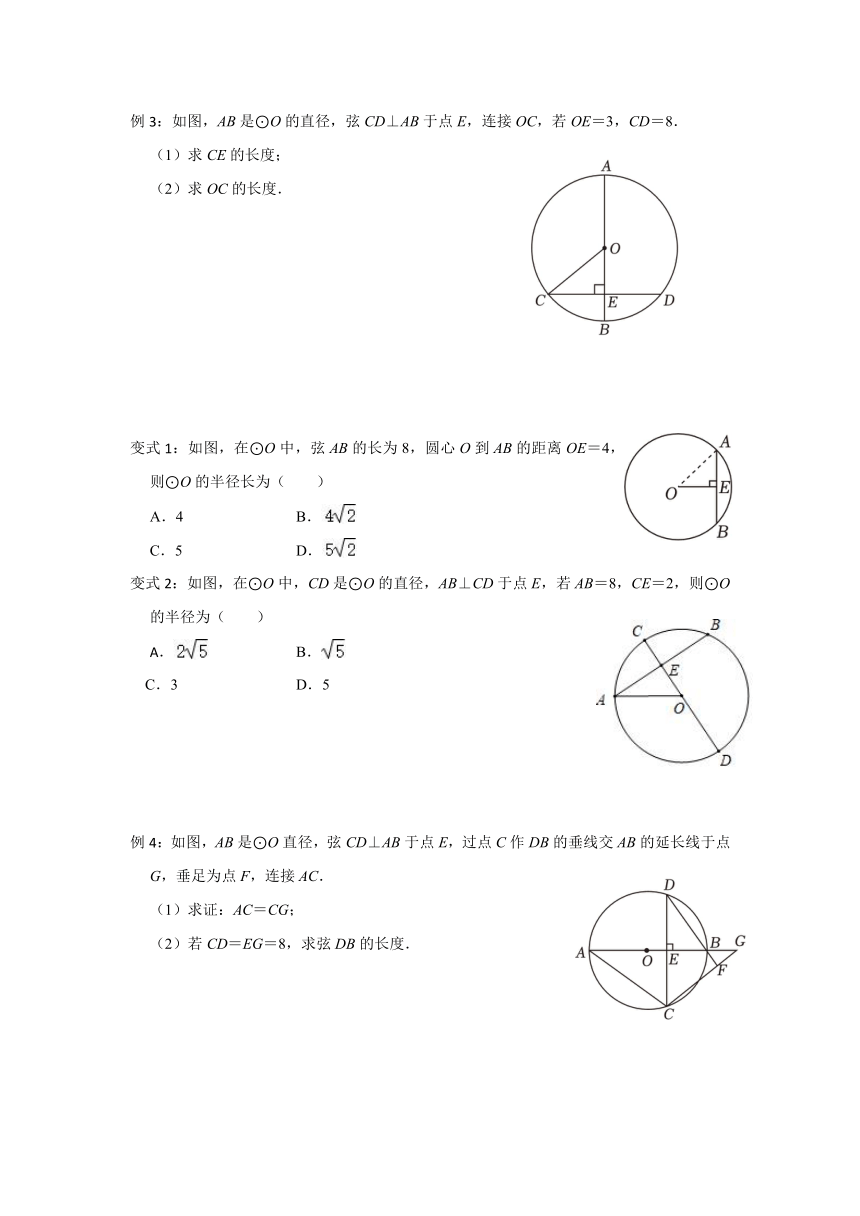
例1:如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,OE=3,那么线段CD的长为( )
A.10 B.8
C.6 D.4
例2:如图,在⊙O中,AB是直径,CD是弦,且AB⊥CD于点E,CD=6,BE=1.求⊙O的半径.
例3:如图,AB是⊙O的直径,弦CD⊥AB于点E,连接OC,若OE=3,CD=8.
(1)求CE的长度;
(2)求OC的长度.
变式1:如图,在⊙O中,弦AB的长为8,圆心O到AB的距离OE=4,则⊙O的半径长为( )
A.4 B.
C.5 D.
变式2:如图,在⊙O中,CD是⊙O的直径,AB⊥CD于点E,若AB=8,CE=2,则⊙O的半径为( )
B.
C.3 D.5
例4:如图,AB是⊙O直径,弦CD⊥AB于点E,过点C作DB的垂线交AB的延长线于点G,垂足为点F,连接AC.
(1)求证:AC=CG;
(2)若CD=EG=8,求弦DB的长度.
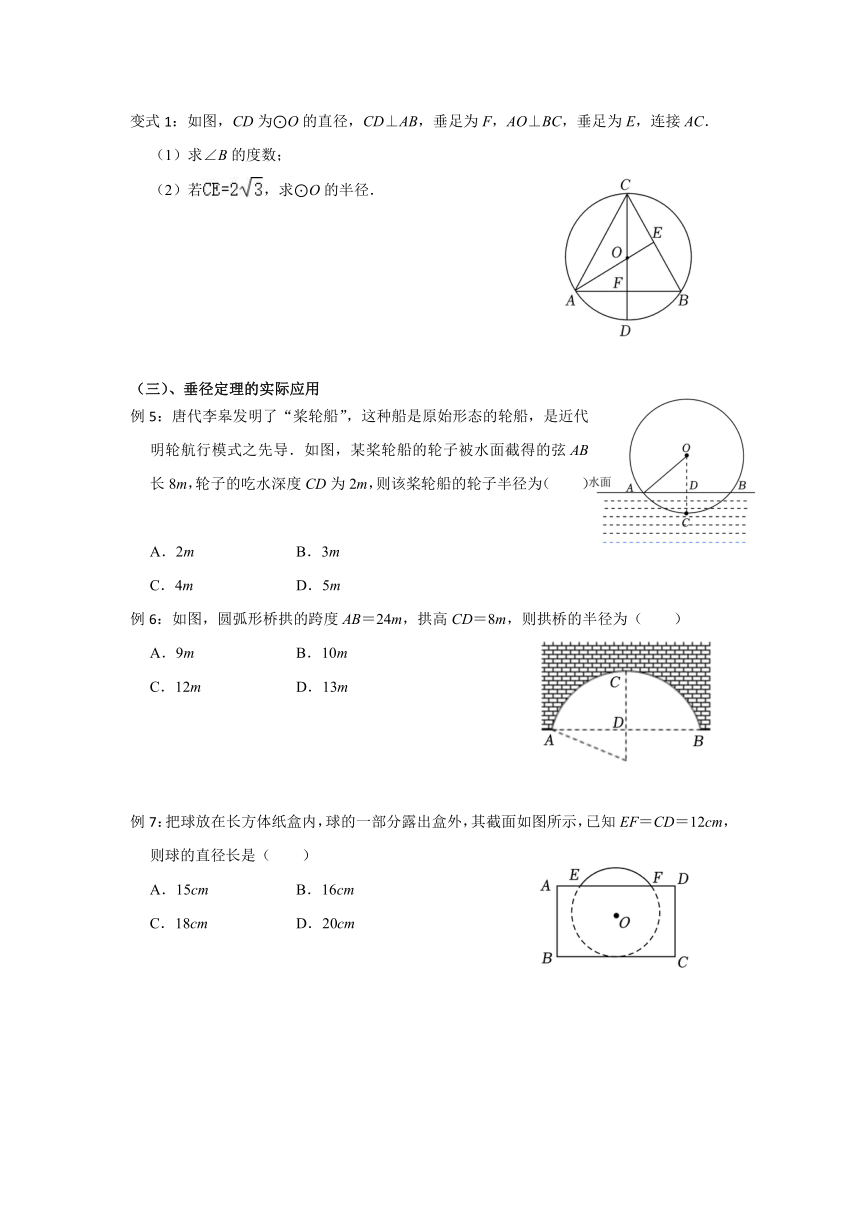
变式1:如图,CD为⊙O的直径,CD⊥AB,垂足为F,AO⊥BC,垂足为E,连接AC.
(1)求∠B的度数;
(2)若,求⊙O的半径.
(三)、垂径定理的实际应用
例5:唐代李皋发明了“桨轮船”,这种船是原始形态的轮船,是近代明轮航行模式之先导.如图,某桨轮船的轮子被水面截得的弦AB长8m,轮子的吃水深度CD为2m,则该桨轮船的轮子半径为( )
A.2m B.3m
C.4m D.5m
例6:如图,圆弧形桥拱的跨度AB=24m,拱高CD=8m,则拱桥的半径为( )
A.9m B.10m
C.12m D.13m
例7:把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=12cm,则球的直径长是( )
A.15cm B.16cm
C.18cm D.20cm
例8:如图、,一弓形弦长为cm,弓形所在的圆的半径为7cm,则弓形的高为 cm.
变式1:已知⊙O中,弦AB=8cm,圆心到AB的距离为3cm,则此圆的半径为 cm.
变式2:⊙O的直径AB=20cm,∠BAC=30°,则弦AC= cm. .
变式3:已知⊙O的半径为10cm,弦MN∥EF,且MN=12cm,EF=16cm,则弦MN和EF之间的距离发为 cm.
三、课后练习
1.如图,在平面直角坐标系中,一个圆与两坐标轴分别交于A、B、C、D四点.已知A(6,0),B(0,3),C(﹣2,0),则点D的坐标为( )
(0,﹣1) B.(0,﹣2)
C.(0,﹣3) D.(0,﹣4)
2.如图,圆柱形水管内积水的水平面宽AB=8cm,水深CD=2cm.则水管的半径是( )
A.4cm B.5cm
C.6cm D.7cm
3.筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1.筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2.已知圆心O在水面上方,且⊙O被水面截得的弦AB长为8米,⊙O半径长为5米.若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是( )
A.1米 B.2米 C.3米 D.4米
4.如图,一条公路的转弯处是一段圆弧(图中的弧,点O是这段弧所在圆的圆心,点C是上一点,OC⊥AB,垂足为点D,AB=300m,CD=50m,则弧所在圆的半径是( )
A.150m B.250m C.300m D.350m
5. 如图,⊙O的直径为10,弦AB=8,P为AB上的一个动点,则OP长的取值范围 .
6.某村为了促进农村经济发展,建设了蔬菜基地,新建了一批蔬菜大棚.如图是蔬菜大棚的截面,形状为圆弧型,圆心为O,跨度AB(弧所对的弦)的长为8米,拱高CD(弧的中点到弦的距离)为2米.
(1)求该圆弧所在圆的半径;
(2)在修建过程中,在距蔬菜大棚的一端(点B)1米处将竖立支撑杆EF,求支撑杆EF的高度.
7.苏州是一座拥有4000多年历史的文化名城,苏州古城座落在水网之中,街道依河而建,水陆并行;建筑临水而造,前巷后河,形成“小桥、流水、人家”的独特风貌.如图,某座苏州古桥的桥拱可看作一段圆弧,现测得桥下水面AB宽度16m时,拱顶高出水平面4m.
(1)求此圆弧形拱桥的半径;
(2)若有一艘宽12m的船准备从桥下穿过,船舱顶部为矩形并高出水面3m,请通过计算判断,该船能否安全穿过桥洞,并说明理由.
8 如图,一条公路的转弯处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD,垂足为F,EF=90m. 求这段弯路的半径.
9. 如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.
10. 如图,某新建公园有一个圆形人工湖,湖中心O处有一座喷泉,小明为测量湖的半径,在湖边选择A、B两个点,在A处测得∠OAB=45°,在AB延长线上的C处测得∠OCA=30°,已知BC=50米,求人工湖的半径.(结果保留根号)
11.如图,在等腰△ABC中,AB=AC,⊙A交BC于D,E两点,半径AF⊥BC于H.
(1)求证:BD=CE;
(2)若DE=8,FH=2,求⊙A的半径.
12.如图,一条公路的转弯处是一段圆弧,点O是这段弧所在圆的圆心,AB=200m,C是上一点,OC⊥AB,垂足为D,CD=50m.求这段弯路的半径.
13.如图,以AB为直径的半圆O上有一点C,过点C作CD⊥OA,垂足为点D,过点A作AE⊥OC,垂足为点E(不与点O,C重合),AE的延长线交半圆O于点F.求证:.
14.如图,有一座圆弧形拱桥,桥下水面宽AB为16m,拱高CN为4m.
(1)求桥拱的半径;
(2)此桥的安全限度是拱顶C点距离水面不得小于1.5m,若大雨过后,洪水泛滥到水面宽度DE为12m时,是否需要采取紧急措施?请说明理由.
15.如图1,装有水的水槽放置在水平桌面上,其横截面是以AB为直径的半圆O,AB=52cm,MN为水面截线,MN=48cm,GH为桌面截线,MN∥GH.
(1)作OC⊥MN于点C,求OC的长;
(2)将图中的水倒出一部分得到图2,发现水面高度下降了14cm,求此时水面截线减少了多少.
16.如图,在△ABC中,∠C=90°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,BC=6.
(1)若∠A=35°,求的长度;
(2)若AC=8,求BD的长.
一、知识梳理
(一)垂径定理及其推论
问题:如图,AB是⊙O的一条弦,直径CD⊥AB, 垂足为E. 图中相等的线段和劣弧有哪些 为什么
归纳总结:
垂径定理: .
数学语言: .
想一想:下列图形是否具备垂径定理的条件?如果不是,请说明为什么?
归纳总结:
垂径定理的几个基本图形:
思考探索:
(1)如果把垂径定理(垂直于弦的直径平分弦,并且平分弦所对的两条弧)结论与题设交换一条,命题是真命题吗?
(2) 以下五个条件中:①过圆心;②垂直于弦;③平分弦;④平分弦所对的优弧;⑤平分弦所对的劣弧. 任何两个条件都可以推出其他三个结论吗?任选一种组合证明你的猜想.
证明举例: 如图,AB是⊙O的一条弦,作直径CD,使AE=BE.
(1)CD⊥AB吗?为什么?
(2)弧AC与弧BC相等吗? 弧AD与弧BD相等吗?为什么?
归纳总结:
垂径定理的推论: .
数学语言: .
思考:“不是直径”这个条件能去掉吗?如果不能,请举出反例.
二、典例精析
(二)垂径定理及其推论的计算
例1:如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,OE=3,那么线段CD的长为( )
A.10 B.8
C.6 D.4
例2:如图,在⊙O中,AB是直径,CD是弦,且AB⊥CD于点E,CD=6,BE=1.求⊙O的半径.
例3:如图,AB是⊙O的直径,弦CD⊥AB于点E,连接OC,若OE=3,CD=8.
(1)求CE的长度;
(2)求OC的长度.
变式1:如图,在⊙O中,弦AB的长为8,圆心O到AB的距离OE=4,则⊙O的半径长为( )
A.4 B.
C.5 D.
变式2:如图,在⊙O中,CD是⊙O的直径,AB⊥CD于点E,若AB=8,CE=2,则⊙O的半径为( )
B.
C.3 D.5
例4:如图,AB是⊙O直径,弦CD⊥AB于点E,过点C作DB的垂线交AB的延长线于点G,垂足为点F,连接AC.
(1)求证:AC=CG;
(2)若CD=EG=8,求弦DB的长度.
变式1:如图,CD为⊙O的直径,CD⊥AB,垂足为F,AO⊥BC,垂足为E,连接AC.
(1)求∠B的度数;
(2)若,求⊙O的半径.
(三)、垂径定理的实际应用
例5:唐代李皋发明了“桨轮船”,这种船是原始形态的轮船,是近代明轮航行模式之先导.如图,某桨轮船的轮子被水面截得的弦AB长8m,轮子的吃水深度CD为2m,则该桨轮船的轮子半径为( )
A.2m B.3m
C.4m D.5m
例6:如图,圆弧形桥拱的跨度AB=24m,拱高CD=8m,则拱桥的半径为( )
A.9m B.10m
C.12m D.13m
例7:把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=12cm,则球的直径长是( )
A.15cm B.16cm
C.18cm D.20cm
例8:如图、,一弓形弦长为cm,弓形所在的圆的半径为7cm,则弓形的高为 cm.
变式1:已知⊙O中,弦AB=8cm,圆心到AB的距离为3cm,则此圆的半径为 cm.
变式2:⊙O的直径AB=20cm,∠BAC=30°,则弦AC= cm. .
变式3:已知⊙O的半径为10cm,弦MN∥EF,且MN=12cm,EF=16cm,则弦MN和EF之间的距离发为 cm.
三、课后练习
1.如图,在平面直角坐标系中,一个圆与两坐标轴分别交于A、B、C、D四点.已知A(6,0),B(0,3),C(﹣2,0),则点D的坐标为( )
(0,﹣1) B.(0,﹣2)
C.(0,﹣3) D.(0,﹣4)
2.如图,圆柱形水管内积水的水平面宽AB=8cm,水深CD=2cm.则水管的半径是( )
A.4cm B.5cm
C.6cm D.7cm
3.筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1.筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2.已知圆心O在水面上方,且⊙O被水面截得的弦AB长为8米,⊙O半径长为5米.若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是( )
A.1米 B.2米 C.3米 D.4米
4.如图,一条公路的转弯处是一段圆弧(图中的弧,点O是这段弧所在圆的圆心,点C是上一点,OC⊥AB,垂足为点D,AB=300m,CD=50m,则弧所在圆的半径是( )
A.150m B.250m C.300m D.350m
5. 如图,⊙O的直径为10,弦AB=8,P为AB上的一个动点,则OP长的取值范围 .
6.某村为了促进农村经济发展,建设了蔬菜基地,新建了一批蔬菜大棚.如图是蔬菜大棚的截面,形状为圆弧型,圆心为O,跨度AB(弧所对的弦)的长为8米,拱高CD(弧的中点到弦的距离)为2米.
(1)求该圆弧所在圆的半径;
(2)在修建过程中,在距蔬菜大棚的一端(点B)1米处将竖立支撑杆EF,求支撑杆EF的高度.
7.苏州是一座拥有4000多年历史的文化名城,苏州古城座落在水网之中,街道依河而建,水陆并行;建筑临水而造,前巷后河,形成“小桥、流水、人家”的独特风貌.如图,某座苏州古桥的桥拱可看作一段圆弧,现测得桥下水面AB宽度16m时,拱顶高出水平面4m.
(1)求此圆弧形拱桥的半径;
(2)若有一艘宽12m的船准备从桥下穿过,船舱顶部为矩形并高出水面3m,请通过计算判断,该船能否安全穿过桥洞,并说明理由.
8 如图,一条公路的转弯处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD,垂足为F,EF=90m. 求这段弯路的半径.
9. 如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.
10. 如图,某新建公园有一个圆形人工湖,湖中心O处有一座喷泉,小明为测量湖的半径,在湖边选择A、B两个点,在A处测得∠OAB=45°,在AB延长线上的C处测得∠OCA=30°,已知BC=50米,求人工湖的半径.(结果保留根号)
11.如图,在等腰△ABC中,AB=AC,⊙A交BC于D,E两点,半径AF⊥BC于H.
(1)求证:BD=CE;
(2)若DE=8,FH=2,求⊙A的半径.
12.如图,一条公路的转弯处是一段圆弧,点O是这段弧所在圆的圆心,AB=200m,C是上一点,OC⊥AB,垂足为D,CD=50m.求这段弯路的半径.
13.如图,以AB为直径的半圆O上有一点C,过点C作CD⊥OA,垂足为点D,过点A作AE⊥OC,垂足为点E(不与点O,C重合),AE的延长线交半圆O于点F.求证:.
14.如图,有一座圆弧形拱桥,桥下水面宽AB为16m,拱高CN为4m.
(1)求桥拱的半径;
(2)此桥的安全限度是拱顶C点距离水面不得小于1.5m,若大雨过后,洪水泛滥到水面宽度DE为12m时,是否需要采取紧急措施?请说明理由.
15.如图1,装有水的水槽放置在水平桌面上,其横截面是以AB为直径的半圆O,AB=52cm,MN为水面截线,MN=48cm,GH为桌面截线,MN∥GH.
(1)作OC⊥MN于点C,求OC的长;
(2)将图中的水倒出一部分得到图2,发现水面高度下降了14cm,求此时水面截线减少了多少.
16.如图,在△ABC中,∠C=90°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,BC=6.
(1)若∠A=35°,求的长度;
(2)若AC=8,求BD的长.
同课章节目录
