2024—2025学年北师大版数学八年级上册期末复习测试A卷(无答案)
文档属性
| 名称 | 2024—2025学年北师大版数学八年级上册期末复习测试A卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 211.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-04 21:58:47 | ||
图片预览

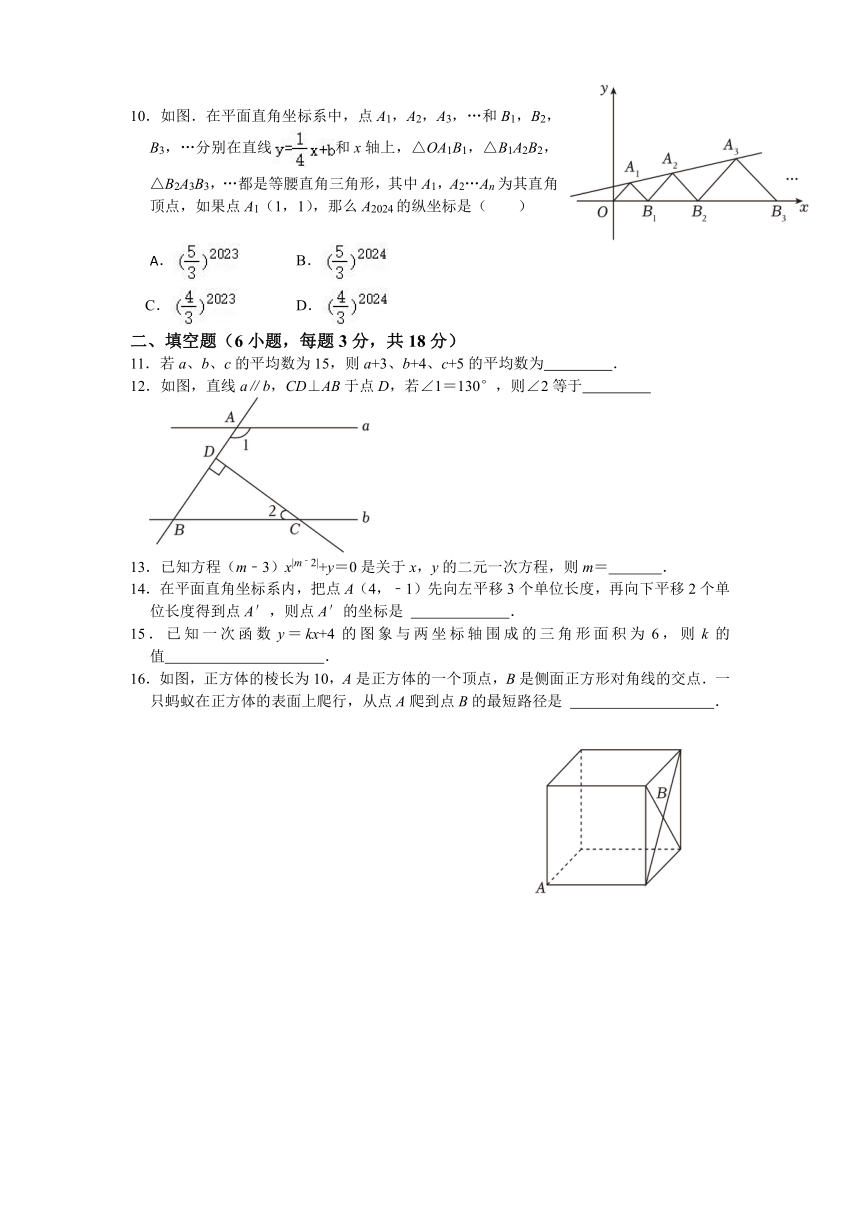
文档简介
2024—2025学年北师大版数学八年级上册期末复习测试A卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列长度的三条线段能组成直角三角形的是( )
A.1,2,3 B.2,3,4 C.3,4,5 D.6,8,9
2.在实数、0、、906、π、0.101中,无理数的个数是( )
A.2个 B.3个 C.4个 D.5个
3.已知:点B的坐标为(3,﹣4),而直线AB平行于y轴,那么A点坐标有可能为( )
A.(3,﹣2) B.(2,4) C.(﹣3,2) D.(﹣3,﹣4)
4.如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲 乙 丙 丁
平均数(cm) 180 185 180 185
方差 8.1 7.4 3.6 3.6
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
5.在英文句“We like math”中,字母“e”出现的频率为( )
A.0.1 B.0.2 C.0.3 D.0.4
6.在平面直角坐标系中,点P的坐标是(3,﹣5),则点P所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.已知一次函数y=﹣2x+4,下列说法错误的是( )
A.图象经过第一、二、四象限
B.图象与x轴的交点坐标为(4,0)
C.y随x增大而减小
D.该图象可以由y=﹣2x平移得到
8.《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架,其中《盈不足》卷记载了一道有趣的数学问题:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”译文:“今有人合伙购物,每人出8钱,会多出3钱;每人出7钱,又差4钱.问人数、物价各多少?”设人数为x人,物价为y钱,根据题意,下面所列方程组正确的是( )
A. B. C. D.
9.若方程组的解中x+y=2024,则k等于( )
A.2024 B.2025 C.2026 D.2027
10.如图.在平面直角坐标系中,点A1,A2,A3,…和B1,B2,B3,…分别在直线和x轴上,△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,其中A1,A2…An为其直角顶点,如果点A1(1,1),那么A2024的纵坐标是( )
B.
C. D.
二、填空题(6小题,每题3分,共18分)
11.若a、b、c的平均数为15,则a+3、b+4、c+5的平均数为 .
12.如图,直线a∥b,CD⊥AB于点D,若∠1=130°,则∠2等于
13.已知方程(m﹣3)x|m﹣2|+y=0是关于x,y的二元一次方程,则m= .
14.在平面直角坐标系内,把点A(4,﹣1)先向左平移3个单位长度,再向下平移2个单位长度得到点A′,则点A′的坐标是 .
15.已知一次函数y=kx+4的图象与两坐标轴围成的三角形面积为6,则k的值 .
16.如图,正方体的棱长为10,A是正方体的一个顶点,B是侧面正方形对角线的交点.一只蚂蚁在正方体的表面上爬行,从点A爬到点B的最短路径是 .
第II卷
2024—2025学年北师大版数学八年级上册期末复习测试A卷
姓名:____________ 学号:____________准考证号:___________
题号 一 二 三 总分
17 18 19 20 21 22 23 24 25
得分
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:
(1); (2)﹣12024+.
18.已知方程组的解和方程组的解相同,求(2a+b)2024的值.
19.如图所示,在平面直角坐标系中,已知A(0,2),B(2,0),C(4,3).
(1)在图中画出△ABC并标出字母,△ABC的面积为 ;
(2)若点P与点C关于y轴对称,则点P的坐标为 ;
(3)已知Q为y轴上一点,若△ACQ的面积为8,请直接写出点Q的坐标.
20.如图,已知点E、F在直线AB上,点G在线段CD上,连接ED、FG交于点H,连接CE并延长到点M,∠CED=∠GHD,∠C=∠EFG.
(1)求证:AB∥CD;
(2)若DE⊥GF,∠D=26°,求∠BEC的度数.
21.为弘扬向善、为善优秀品质,助力爱心公益事业,某校组织开展“人间自有真情在”的捐款活动,八年级全体同学参加了此次活动.随机抽查了部分同学捐款的情况,统计结果如图1和图2所示.
(1)本次抽查的学生人数是 ,并补全条形统计图;
(2)本次捐款金额的众数为 元,中位数为 元;
(3)若这所学校八年级学生为800名,捐款总金额约有多少元?
22.在平面直角坐标系中,有一点P(2x﹣1,3x).
(1)若点P在y轴上,求x的值;
(2)若Q(5,8),且PQ∥y轴,求出点P的坐标;
(3)若点P在第一象限,且到两坐标轴的距离之和为9,求点P的坐标.
23.张老师在某文体店购买商品A、B若干次(每次A、B两种商品都购买,且A、B都只能购买整数个),其中第一、二两次购买时,均按标价购买,两次购买商品A、B的数量和费用如表所示:
购买商品A的数量/个 购买商品B的数量/个 购买总费用/元
第一次购物 6 5 980
第二次购物 3 7 940
(1)求商品A、B的标价;
(2)若张老师第三次购物时,商品A、B同时打6折出售,这次购买总费用为960元,则张老师有哪几种购买方案?
24.我们规定,在平面直角坐标系中,对于点P0(m,n)作如下“可持续发展”变换:若m≥n,则作它关于x轴的对称点;若m<n,则作它关于y轴的对称点.点P0作第一次“可持续发展”变换得到点P1,再将点P1作第二次“可持续发展”变换得到点P2.若P0与P2重合,我们称点P0为“可持续发展点”;若P0与P2不重合,我们称点P0为“合作共赢点”.
(1)将点P0(3,2)作如上“可持续发展”变换,则点P1的坐标为 ,点P2的坐标为 ,由此,点P0为“ 点”(填“可持续发展”或“合作共赢”);
(2)若点P0(m+n)为第三象限中的一点,求证:P0必为“合作共赢点”,且S=2mn;
(3)若点P0(m,n)为第三象限中的一点,且P0P1=18,S=18.若t为实数,m>n,当|t2﹣mn|﹣m=10+n时,求出t的值和P0的坐标.
25.如图,在平面直角坐标系xOy中,直线l1:y=﹣的图象与x轴、y轴分别交于D,B两点.直线y=kx+的图象与x轴交于C.直线l1与直线l2交于点A(a,3).
(1)求点A的坐标及直线l2的表达式;
(2)若点E在直线l2上,且△ADE的面积为,求点E的坐标;
(3)在x轴上是否存在点P,使得∠ACB=2∠APC,若存在,求出点P坐标,若不存在,说明理由.
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列长度的三条线段能组成直角三角形的是( )
A.1,2,3 B.2,3,4 C.3,4,5 D.6,8,9
2.在实数、0、、906、π、0.101中,无理数的个数是( )
A.2个 B.3个 C.4个 D.5个
3.已知:点B的坐标为(3,﹣4),而直线AB平行于y轴,那么A点坐标有可能为( )
A.(3,﹣2) B.(2,4) C.(﹣3,2) D.(﹣3,﹣4)
4.如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲 乙 丙 丁
平均数(cm) 180 185 180 185
方差 8.1 7.4 3.6 3.6
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
5.在英文句“We like math”中,字母“e”出现的频率为( )
A.0.1 B.0.2 C.0.3 D.0.4
6.在平面直角坐标系中,点P的坐标是(3,﹣5),则点P所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.已知一次函数y=﹣2x+4,下列说法错误的是( )
A.图象经过第一、二、四象限
B.图象与x轴的交点坐标为(4,0)
C.y随x增大而减小
D.该图象可以由y=﹣2x平移得到
8.《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架,其中《盈不足》卷记载了一道有趣的数学问题:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”译文:“今有人合伙购物,每人出8钱,会多出3钱;每人出7钱,又差4钱.问人数、物价各多少?”设人数为x人,物价为y钱,根据题意,下面所列方程组正确的是( )
A. B. C. D.
9.若方程组的解中x+y=2024,则k等于( )
A.2024 B.2025 C.2026 D.2027
10.如图.在平面直角坐标系中,点A1,A2,A3,…和B1,B2,B3,…分别在直线和x轴上,△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,其中A1,A2…An为其直角顶点,如果点A1(1,1),那么A2024的纵坐标是( )
B.
C. D.
二、填空题(6小题,每题3分,共18分)
11.若a、b、c的平均数为15,则a+3、b+4、c+5的平均数为 .
12.如图,直线a∥b,CD⊥AB于点D,若∠1=130°,则∠2等于
13.已知方程(m﹣3)x|m﹣2|+y=0是关于x,y的二元一次方程,则m= .
14.在平面直角坐标系内,把点A(4,﹣1)先向左平移3个单位长度,再向下平移2个单位长度得到点A′,则点A′的坐标是 .
15.已知一次函数y=kx+4的图象与两坐标轴围成的三角形面积为6,则k的值 .
16.如图,正方体的棱长为10,A是正方体的一个顶点,B是侧面正方形对角线的交点.一只蚂蚁在正方体的表面上爬行,从点A爬到点B的最短路径是 .
第II卷
2024—2025学年北师大版数学八年级上册期末复习测试A卷
姓名:____________ 学号:____________准考证号:___________
题号 一 二 三 总分
17 18 19 20 21 22 23 24 25
得分
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:
(1); (2)﹣12024+.
18.已知方程组的解和方程组的解相同,求(2a+b)2024的值.
19.如图所示,在平面直角坐标系中,已知A(0,2),B(2,0),C(4,3).
(1)在图中画出△ABC并标出字母,△ABC的面积为 ;
(2)若点P与点C关于y轴对称,则点P的坐标为 ;
(3)已知Q为y轴上一点,若△ACQ的面积为8,请直接写出点Q的坐标.
20.如图,已知点E、F在直线AB上,点G在线段CD上,连接ED、FG交于点H,连接CE并延长到点M,∠CED=∠GHD,∠C=∠EFG.
(1)求证:AB∥CD;
(2)若DE⊥GF,∠D=26°,求∠BEC的度数.
21.为弘扬向善、为善优秀品质,助力爱心公益事业,某校组织开展“人间自有真情在”的捐款活动,八年级全体同学参加了此次活动.随机抽查了部分同学捐款的情况,统计结果如图1和图2所示.
(1)本次抽查的学生人数是 ,并补全条形统计图;
(2)本次捐款金额的众数为 元,中位数为 元;
(3)若这所学校八年级学生为800名,捐款总金额约有多少元?
22.在平面直角坐标系中,有一点P(2x﹣1,3x).
(1)若点P在y轴上,求x的值;
(2)若Q(5,8),且PQ∥y轴,求出点P的坐标;
(3)若点P在第一象限,且到两坐标轴的距离之和为9,求点P的坐标.
23.张老师在某文体店购买商品A、B若干次(每次A、B两种商品都购买,且A、B都只能购买整数个),其中第一、二两次购买时,均按标价购买,两次购买商品A、B的数量和费用如表所示:
购买商品A的数量/个 购买商品B的数量/个 购买总费用/元
第一次购物 6 5 980
第二次购物 3 7 940
(1)求商品A、B的标价;
(2)若张老师第三次购物时,商品A、B同时打6折出售,这次购买总费用为960元,则张老师有哪几种购买方案?
24.我们规定,在平面直角坐标系中,对于点P0(m,n)作如下“可持续发展”变换:若m≥n,则作它关于x轴的对称点;若m<n,则作它关于y轴的对称点.点P0作第一次“可持续发展”变换得到点P1,再将点P1作第二次“可持续发展”变换得到点P2.若P0与P2重合,我们称点P0为“可持续发展点”;若P0与P2不重合,我们称点P0为“合作共赢点”.
(1)将点P0(3,2)作如上“可持续发展”变换,则点P1的坐标为 ,点P2的坐标为 ,由此,点P0为“ 点”(填“可持续发展”或“合作共赢”);
(2)若点P0(m+n)为第三象限中的一点,求证:P0必为“合作共赢点”,且S=2mn;
(3)若点P0(m,n)为第三象限中的一点,且P0P1=18,S=18.若t为实数,m>n,当|t2﹣mn|﹣m=10+n时,求出t的值和P0的坐标.
25.如图,在平面直角坐标系xOy中,直线l1:y=﹣的图象与x轴、y轴分别交于D,B两点.直线y=kx+的图象与x轴交于C.直线l1与直线l2交于点A(a,3).
(1)求点A的坐标及直线l2的表达式;
(2)若点E在直线l2上,且△ADE的面积为,求点E的坐标;
(3)在x轴上是否存在点P,使得∠ACB=2∠APC,若存在,求出点P坐标,若不存在,说明理由.
同课章节目录
