2024—2025学年北师大版数学九年级上册期末复习测试A卷(无答案)
文档属性
| 名称 | 2024—2025学年北师大版数学九年级上册期末复习测试A卷(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 221.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-04 22:02:50 | ||
图片预览


文档简介
2024—2025学年北师大版数学九年级上册期末复习测试A卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列立体图形中,从前面看得到的平面图形与从左面看得到的平面图形不相同的是( )
A.长方体B.正方体 C.圆柱D.球
2.一个口袋中有红球、白球共10个,这些球除颜色外都相同.将口袋中的球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回口袋中.不断重复这一过程,共摸了100次球,发现有69次摸到红球,请估计这个口袋中白球的数量为( )
A.7 B.6 C.4 D.3
3.一元二次方程x2﹣x=3的根的情况是( )
A.没有实数根 B.有一个实数根
C.有两个相等的实数根 D.有两个不相等的实数根
4.下列说法正确的是( )
A.对角线互相垂直的平行四边形是正方形
B.一组对边平行另一组对边相等的四边形是平行四边形
C.一组对边平行且一组对角相等的四边形是平行四边形
D.对角线互相垂直的四边形是菱形
5.已知a和b是方程x2+2024x﹣4=0的两个解,则a2+2023a﹣b的值为( )
A.2020 B.2024 C.2026 D.2028
6.下列关于反比例函数 的说法正确的是( )
A.图象位于第二、四象限 B.y随x的增大而减小
C.函数图象过点(﹣2,4) D.图象是中心对称图形
7.某人患了流感,经过两轮传染后共有36人患了流感.设每一轮传染中平均每人传染了x人,则可得到方程( )
A.x+(1+x)=36 B.2(1+x)=36
C.1+x+x(1+x)=36 D.1+x+x2=36
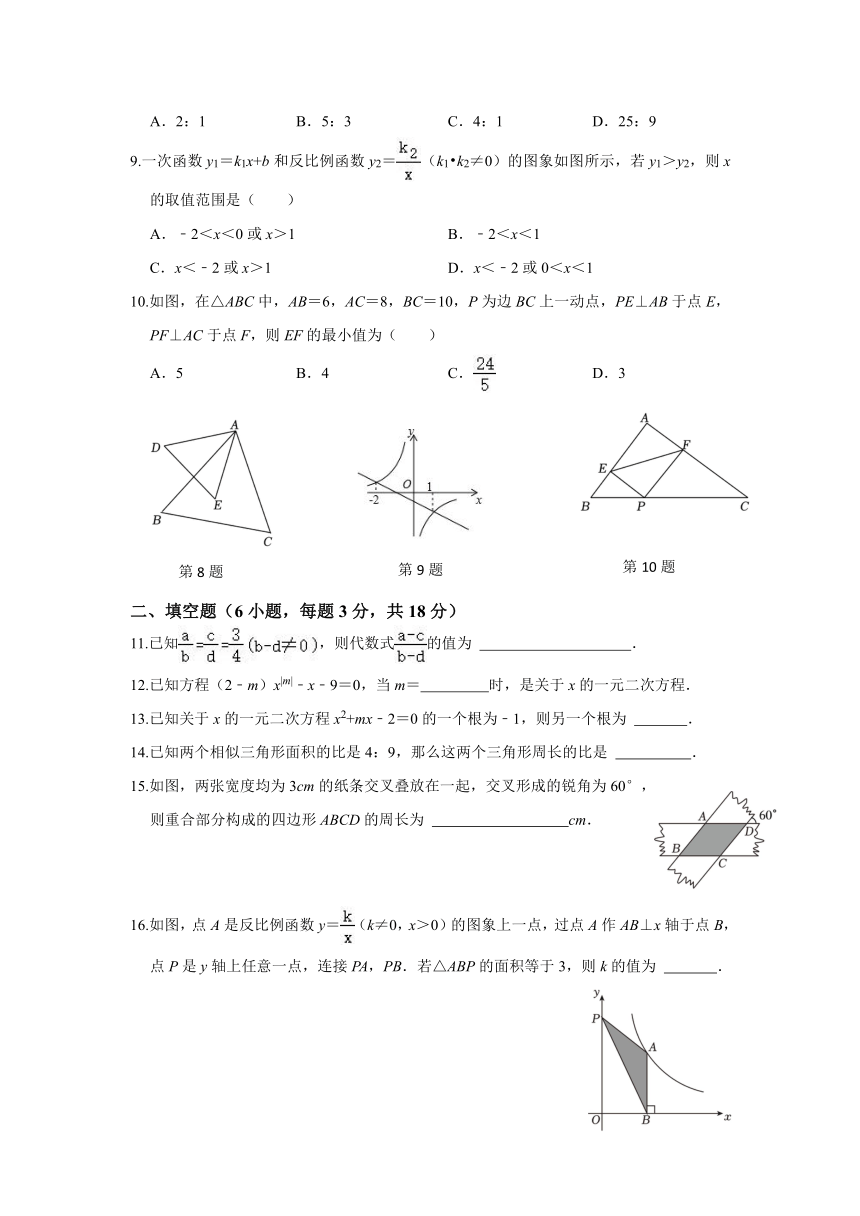
8.如图,△ABC∽△AED,若AD=3,AB=5,AC=6,则S△ABC:S△AED的值为( )
A.2:1 B.5:3 C.4:1 D.25:9
9.一次函数y1=k1x+b和反比例函数y2=(k1 k2≠0)的图象如图所示,若y1>y2,则x的取值范围是( )
A.﹣2<x<0或x>1 B.﹣2<x<1
C.x<﹣2或x>1 D.x<﹣2或0<x<1
10.如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于点E,PF⊥AC于点F,则EF的最小值为( )
A.5 B.4 C. D.3
二、填空题(6小题,每题3分,共18分)
11.已知,则代数式的值为 .
12.已知方程(2﹣m)x|m|﹣x﹣9=0,当m= 时,是关于x的一元二次方程.
13.已知关于x的一元二次方程x2+mx﹣2=0的一个根为﹣1,则另一个根为 .
14.已知两个相似三角形面积的比是4:9,那么这两个三角形周长的比是 .
15.如图,两张宽度均为3cm的纸条交叉叠放在一起,交叉形成的锐角为60°,则重合部分构成的四边形ABCD的周长为 cm.
16.如图,点A是反比例函数y=(k≠0,x>0)的图象上一点,过点A作AB⊥x轴于点B,点P是y轴上任意一点,连接PA,PB.若△ABP的面积等于3,则k的值为 .
第II卷
2024—2025学年北师大版数学九年级上册期末复习测试A卷
姓名:____________ 学号:____________准考证号:___________
题号 一 二 三 总分
17 18 19 20 21 22 23 24 25
得分
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解下列方程:
(1)(x﹣1)(x+3)=x﹣1; (2)2x2﹣6x=﹣3.
18.如图:已知 ABCD,过点A的直线交BC的延长线于E,交BD、CD于F、G.
(1)若AB=3,BC=4,CE=2,求CG的长;
(2)证明:AF2=FG×FE.
19.关于x的方程x2﹣2mx+m2﹣m=0有两个不相等的实数根x1,x2.
①求m的取值范围;
②若,求m的值.
20.我市某中学举行“中国梦 我的梦”的演讲比赛,赛后整理参赛学生的成绩,将学生的成绩分为A、B、C、D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整,请你根据统计图解答下列问题.
(1)该中学参加比赛的学生共有 人,成绩为“B等级”的学生有 人,在扇形统计图中,表示“D等级”的扇形的圆心角为 度,图中m的值为 ;
(2)组委会决定从本次比赛中获得A等级的学生中,选出两名去参加市中学生演讲比赛,已知A等级中男生只有1名,请用画树状图或列表的方法求出所选学生恰是一男一女的概率.
21.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB,交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形.
(2)若AB=5,BD=6,求OE的长.
22.把边长为2厘米的6个相同正方体摆成如图的形式.
(1)画出从正面看、从左面看,从上面看该几何体得到的形状图.
(2)试求出其表面积.
(3)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体从左面看和从上面看得到的形状图不变,那么最多可以再添加 个小正方体.
23.如图,已知正方形ABCD中,E为CB延长线上一点,且BE=AB,M、N分别为AE、BC的中点,连DE交AB于O,MN交,ED于H点.
(1)求证:AO=BO;
(2)求证:∠HEB=∠HNB;
(3)过A作AP⊥ED于P点,连BP,则的值.
24.如图,AB是⊙O的直径,点C在⊙O上,∠BOC=108°,过点C作直线CD分别交直线AB和⊙O于点D、E,连接OE,DE=AB,OD=2.
(1)求∠CDB的度数;
(2)我们把有一个内角等于36°的等腰三角形称为黄金三角形.它的腰长与底边长的比(或者底边长与腰长的比)等于黄金分割比.
①写出图中所有的黄金三角形,选一个说明理由;
②求弦CE的长;
③在直线AB或CD上是否存在点P(点C、D除外),使△POE是黄金三角形?若存在,画出点P,简要说明画出点P的方法(不要求证明);若不存在,说明理由.
25.如图,直线y1=2x+2与坐标轴交于A、B两点,与双曲线交于C、D两点,并且DA=AB.
(1)求反比例函数的解析式;
(2)若P,Q分别是第一、三象限内反比例函数图象上的两点,连接DP,PQ,QC,当四边形DPQC为平行四边形时,求点Q的坐标;
(3)在(2)的条件下,将CQ所在的直线向上平移m(m>0)个单位长度,平移后的直线与双曲线交于H,R两点,与直线AB交于点G,设H,R,G的横坐标分别为xH,xR,xG,若xH,xR,xG满足等式,求m的值.
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列立体图形中,从前面看得到的平面图形与从左面看得到的平面图形不相同的是( )
A.长方体B.正方体 C.圆柱D.球
2.一个口袋中有红球、白球共10个,这些球除颜色外都相同.将口袋中的球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回口袋中.不断重复这一过程,共摸了100次球,发现有69次摸到红球,请估计这个口袋中白球的数量为( )
A.7 B.6 C.4 D.3
3.一元二次方程x2﹣x=3的根的情况是( )
A.没有实数根 B.有一个实数根
C.有两个相等的实数根 D.有两个不相等的实数根
4.下列说法正确的是( )
A.对角线互相垂直的平行四边形是正方形
B.一组对边平行另一组对边相等的四边形是平行四边形
C.一组对边平行且一组对角相等的四边形是平行四边形
D.对角线互相垂直的四边形是菱形
5.已知a和b是方程x2+2024x﹣4=0的两个解,则a2+2023a﹣b的值为( )
A.2020 B.2024 C.2026 D.2028
6.下列关于反比例函数 的说法正确的是( )
A.图象位于第二、四象限 B.y随x的增大而减小
C.函数图象过点(﹣2,4) D.图象是中心对称图形
7.某人患了流感,经过两轮传染后共有36人患了流感.设每一轮传染中平均每人传染了x人,则可得到方程( )
A.x+(1+x)=36 B.2(1+x)=36
C.1+x+x(1+x)=36 D.1+x+x2=36
8.如图,△ABC∽△AED,若AD=3,AB=5,AC=6,则S△ABC:S△AED的值为( )
A.2:1 B.5:3 C.4:1 D.25:9
9.一次函数y1=k1x+b和反比例函数y2=(k1 k2≠0)的图象如图所示,若y1>y2,则x的取值范围是( )
A.﹣2<x<0或x>1 B.﹣2<x<1
C.x<﹣2或x>1 D.x<﹣2或0<x<1
10.如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于点E,PF⊥AC于点F,则EF的最小值为( )
A.5 B.4 C. D.3
二、填空题(6小题,每题3分,共18分)
11.已知,则代数式的值为 .
12.已知方程(2﹣m)x|m|﹣x﹣9=0,当m= 时,是关于x的一元二次方程.
13.已知关于x的一元二次方程x2+mx﹣2=0的一个根为﹣1,则另一个根为 .
14.已知两个相似三角形面积的比是4:9,那么这两个三角形周长的比是 .
15.如图,两张宽度均为3cm的纸条交叉叠放在一起,交叉形成的锐角为60°,则重合部分构成的四边形ABCD的周长为 cm.
16.如图,点A是反比例函数y=(k≠0,x>0)的图象上一点,过点A作AB⊥x轴于点B,点P是y轴上任意一点,连接PA,PB.若△ABP的面积等于3,则k的值为 .
第II卷
2024—2025学年北师大版数学九年级上册期末复习测试A卷
姓名:____________ 学号:____________准考证号:___________
题号 一 二 三 总分
17 18 19 20 21 22 23 24 25
得分
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解下列方程:
(1)(x﹣1)(x+3)=x﹣1; (2)2x2﹣6x=﹣3.
18.如图:已知 ABCD,过点A的直线交BC的延长线于E,交BD、CD于F、G.
(1)若AB=3,BC=4,CE=2,求CG的长;
(2)证明:AF2=FG×FE.
19.关于x的方程x2﹣2mx+m2﹣m=0有两个不相等的实数根x1,x2.
①求m的取值范围;
②若,求m的值.
20.我市某中学举行“中国梦 我的梦”的演讲比赛,赛后整理参赛学生的成绩,将学生的成绩分为A、B、C、D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整,请你根据统计图解答下列问题.
(1)该中学参加比赛的学生共有 人,成绩为“B等级”的学生有 人,在扇形统计图中,表示“D等级”的扇形的圆心角为 度,图中m的值为 ;
(2)组委会决定从本次比赛中获得A等级的学生中,选出两名去参加市中学生演讲比赛,已知A等级中男生只有1名,请用画树状图或列表的方法求出所选学生恰是一男一女的概率.
21.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB,交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形.
(2)若AB=5,BD=6,求OE的长.
22.把边长为2厘米的6个相同正方体摆成如图的形式.
(1)画出从正面看、从左面看,从上面看该几何体得到的形状图.
(2)试求出其表面积.
(3)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体从左面看和从上面看得到的形状图不变,那么最多可以再添加 个小正方体.
23.如图,已知正方形ABCD中,E为CB延长线上一点,且BE=AB,M、N分别为AE、BC的中点,连DE交AB于O,MN交,ED于H点.
(1)求证:AO=BO;
(2)求证:∠HEB=∠HNB;
(3)过A作AP⊥ED于P点,连BP,则的值.
24.如图,AB是⊙O的直径,点C在⊙O上,∠BOC=108°,过点C作直线CD分别交直线AB和⊙O于点D、E,连接OE,DE=AB,OD=2.
(1)求∠CDB的度数;
(2)我们把有一个内角等于36°的等腰三角形称为黄金三角形.它的腰长与底边长的比(或者底边长与腰长的比)等于黄金分割比.
①写出图中所有的黄金三角形,选一个说明理由;
②求弦CE的长;
③在直线AB或CD上是否存在点P(点C、D除外),使△POE是黄金三角形?若存在,画出点P,简要说明画出点P的方法(不要求证明);若不存在,说明理由.
25.如图,直线y1=2x+2与坐标轴交于A、B两点,与双曲线交于C、D两点,并且DA=AB.
(1)求反比例函数的解析式;
(2)若P,Q分别是第一、三象限内反比例函数图象上的两点,连接DP,PQ,QC,当四边形DPQC为平行四边形时,求点Q的坐标;
(3)在(2)的条件下,将CQ所在的直线向上平移m(m>0)个单位长度,平移后的直线与双曲线交于H,R两点,与直线AB交于点G,设H,R,G的横坐标分别为xH,xR,xG,若xH,xR,xG满足等式,求m的值.
同课章节目录
