2024—2025学年人教版数学九年级上册期末复习测试C卷(无答案)
文档属性
| 名称 | 2024—2025学年人教版数学九年级上册期末复习测试C卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 268.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-04 22:18:10 | ||
图片预览


文档简介
2024—2025学年人教版数学九年级上册期末复习测试C卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分
1.下列图形既是中心对称图形又是轴对称图形的是( )
A. B.
C. D.
2.下列说法正确的是( )
A.对角线相等的四边形是矩形
B.等弧所对的圆心角相等
C.过三点一定可以确定一个圆
D.垂直于半径的直线是圆的切线
3.若抛物线y=(a﹣1)x2﹣a2+1=0经过原点,则a的值是( )
A.±1 B.1 C.﹣1 D.0
4.豫剧是国家级非物质文化遗产,因其雅俗共赏,深受大众喜爱.正面印有豫剧经典剧目《花木兰》、《穆桂英挂帅》、《朝阳沟》、《七品芝麻官》的四张卡片,它们除正面外完全相同.把这四张卡片背面朝上洗匀,随机抽取两张,抽取的卡片为《花木兰》、《七品芝麻官》的概率为( )
A. B. C. D.
5.如图,△ABC中,∠BAC=55°,将△ABC逆时针旋转α(0°<α<55°),得到△ADE,DE交AC于F.当α=40°时,点D恰好落在BC上,此时∠AFE等于( )
A.80° B.85°
C.90° D.95°
6.如图,A、D是⊙O上的两点,A是的中点,若∠D=35°,则∠BCA的度数是( )
A.55° B.45°
C.35° D.25°
7.已知圆锥的底面圆半径为3,母线长为4,则圆锥的侧面积为( )
A.6π B.12π C.15π D.24π
8.将抛物线y=x2+2x向下平移2个单位后,所得新抛物线的顶点式为( )
A.y=(x+1)2﹣3 B.y=(x+1)2﹣2
C.y=(x﹣1)2﹣3 D.y=(x﹣1)2﹣2
9.已知二次函数y=x2﹣2x(﹣1≤x≤t﹣1),当x=﹣1时,函数取得最大值;当x=1时,函数取得最小值,则t的取值范围是( )
A.0<t≤2 B.0<t≤4 C.2≤t≤4 D.t≥2
10.如图,在平面直角坐标系中,Rt△AOB的一条直角边OB在x轴上,点A的坐标为(﹣6,4);Rt△COD中,∠COD=90°,OD=4,∠D=30°,连接BC,点M是BC中点,连接AM.将Rt△COD以点O为旋转中心按顺时针方向旋转,在旋转过程中,线段AM的最小值是( )
A.3 B.6﹣4
C.2﹣2 D.2
二、填空题(6小题,每题3分,共18分)
11.在平面直角坐标系中,若点P(2,﹣1)与点Q(﹣2,m)关于原点对称,则m的值是 .
12.已知是y关于x的二次函数,m= .
13.已知方程x2+x﹣2=0的两根分别为x1,x2,则的值为 .
14.将抛物线y=﹣x2先向右平移1个单位长度,再向上平移2个单位长度,则平移后抛物线的顶点坐标为 .
15.已知抛物线y=x2﹣6x+m与x轴有且只有一个交点,则m= .
16.如图,已知Rt△ABC中,∠ABC=90°,∠ACB=30°,斜边AC=4,点P是三角形内的一动点,则PA+PB+PC的最小值是 .
第II卷
2024—2025学年人教版数学九年级上册期末复习测试C卷
姓名:____________ 学号:____________准考证号:___________
题号 一 二 三 总分
17 18 19 20 21 22 23 24 25
得分
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.已知关于x的一元二次方程x2﹣(2m﹣1)x﹣3m2+m=0.
(1)求证:无论m为何值,方程总有实数根;
(2)若x1,x2是方程的两个实数根,且+=﹣,求m的值.
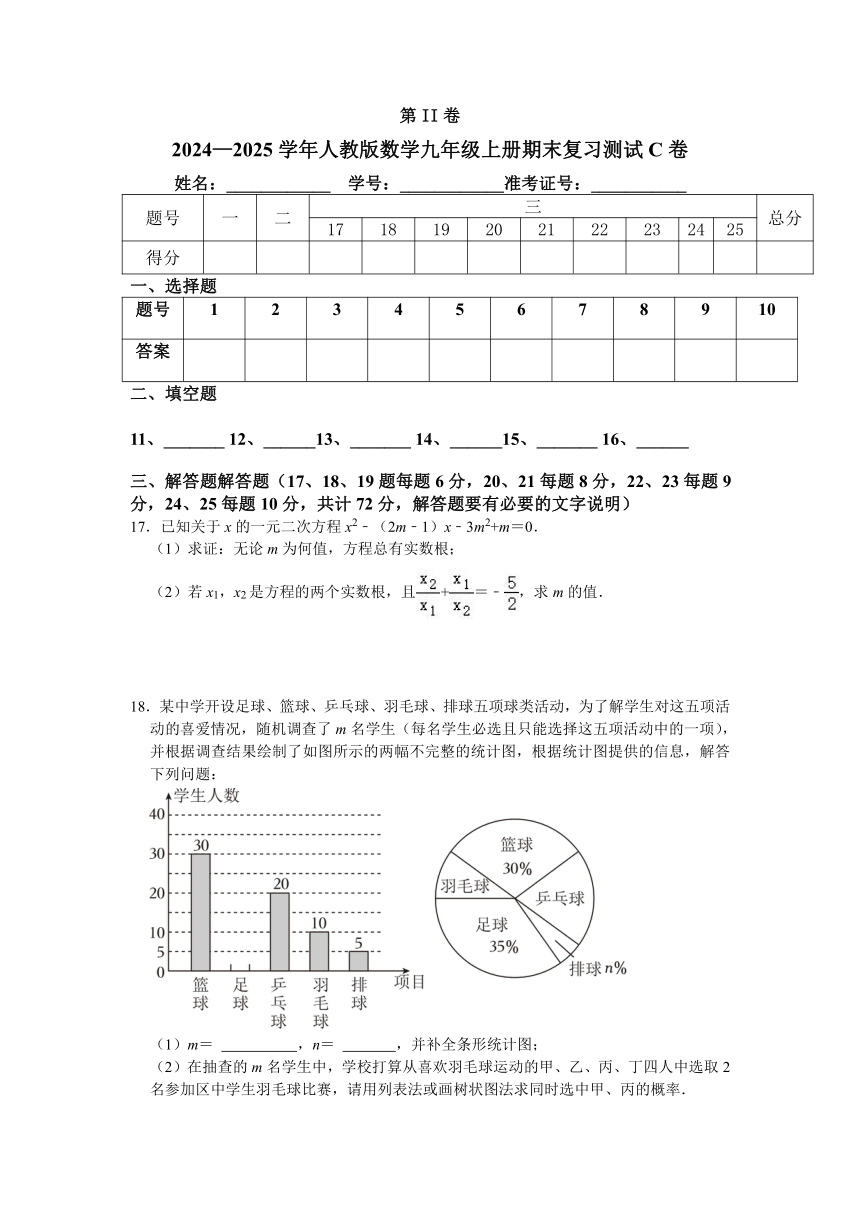
18.某中学开设足球、篮球、乒乓球、羽毛球、排球五项球类活动,为了解学生对这五项活动的喜爱情况,随机调查了m名学生(每名学生必选且只能选择这五项活动中的一项),并根据调查结果绘制了如图所示的两幅不完整的统计图,根据统计图提供的信息,解答下列问题:
(1)m= ,n= ,并补全条形统计图;
(2)在抽查的m名学生中,学校打算从喜欢羽毛球运动的甲、乙、丙、丁四人中选取2名参加区中学生羽毛球比赛,请用列表法或画树状图法求同时选中甲、丙的概率.
19.如图,将△ABC绕点C逆时针旋转90°得△DEC,其中点A,点B的对应点分别是点D,点E,点B落在DE上,延长AC交DE于点F,AB、DC交于点G.
(1)求证:AB⊥DE;
(2)求证:FB+BG=BC.
20.如图,在△ABC中,以AB为直径的⊙O交BC于点D,DE⊥AC,垂足为E.⊙O的两条弦FB,FD相交于点F,∠DAE=∠BFD.
(1)求证:DE是⊙O的切线;
(2)若∠C=30°,CD=2,求扇形OBD的面积.
21.国庆期间某旅游点一家商铺销售一批成本为每件50元的商品,规定销售单价不低于成本价,又不高于每件70元,销售量y(件)与销售单价x(元)的关系可以近似的看作一次函数(如图).
(1)请直接写出y关于x的函数表达式 ;
(2)设该商铺销售这批商品获得的总利润为w元,当销售单价为多少元时,可获得的总利润最大?最大总利润是多少?
22.如图,抛物线与直线y2=kx+c交于B(3,0),C(0,﹣3)两点,抛物线与x轴的另一个交点为A.
(1)b= ;c= ;k= ;
(2)关于x的不等式﹣x2+bx+c<kx+c的解集为 ;
(3)求△ABC的面积.
23.如图,AB是半径为5的⊙O的直径,C是的中点,连接CD交AB于点E,连接AC,AD,OC.
(1)求证:OC⊥AD.
(2)若BE=1,求AD的长.
(3)如图2,作CF⊥AB于点H,交AD于点F,射线CB交AD的延长线于点G,若OH=1,求AG的长.
24.已知二次函数y=x2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.
(1)求抛物线的解析式.
(2)抛物线的对称轴上有一动点P,求出PA+PD值最小时P点的坐标.
(3)在第三象限中的抛物线上是否存在一点Q,使△QAC的面积最大?若存在,求出Q点的坐标及△QAC面积的最大值;若不存在,说明理由.
25.已知抛物线l1:y=ax2+(2b+1)x+2b,直线l2:y=mx+n(0<m<n).
(1)若抛物线l1的对称轴为直线x=1,且经过点(﹣1,0),求该抛物线的解析式;
(2)在(1)的条件下,将抛物线l1图象x轴下方的部分沿x轴向上翻折,得到的新图象记作w,图象w与直线y=t+1恒有四个交点,从左到右四个交点依次记为A,B,C,D,是否存在以BC为直径的圆恰好过点M(1,1)?若存在,求出t的值;若不存在,请说明理由;
(3)若抛物线l1经过(s,﹣4),当a=1,﹣2<b<2时,对于任意实数x,满足ax2+(2b+1)x+2b≥﹣4恒成立;且当m≤x≤n时,恰好有,求直线l2的解析式.
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分
1.下列图形既是中心对称图形又是轴对称图形的是( )
A. B.
C. D.
2.下列说法正确的是( )
A.对角线相等的四边形是矩形
B.等弧所对的圆心角相等
C.过三点一定可以确定一个圆
D.垂直于半径的直线是圆的切线
3.若抛物线y=(a﹣1)x2﹣a2+1=0经过原点,则a的值是( )
A.±1 B.1 C.﹣1 D.0
4.豫剧是国家级非物质文化遗产,因其雅俗共赏,深受大众喜爱.正面印有豫剧经典剧目《花木兰》、《穆桂英挂帅》、《朝阳沟》、《七品芝麻官》的四张卡片,它们除正面外完全相同.把这四张卡片背面朝上洗匀,随机抽取两张,抽取的卡片为《花木兰》、《七品芝麻官》的概率为( )
A. B. C. D.
5.如图,△ABC中,∠BAC=55°,将△ABC逆时针旋转α(0°<α<55°),得到△ADE,DE交AC于F.当α=40°时,点D恰好落在BC上,此时∠AFE等于( )
A.80° B.85°
C.90° D.95°
6.如图,A、D是⊙O上的两点,A是的中点,若∠D=35°,则∠BCA的度数是( )
A.55° B.45°
C.35° D.25°
7.已知圆锥的底面圆半径为3,母线长为4,则圆锥的侧面积为( )
A.6π B.12π C.15π D.24π
8.将抛物线y=x2+2x向下平移2个单位后,所得新抛物线的顶点式为( )
A.y=(x+1)2﹣3 B.y=(x+1)2﹣2
C.y=(x﹣1)2﹣3 D.y=(x﹣1)2﹣2
9.已知二次函数y=x2﹣2x(﹣1≤x≤t﹣1),当x=﹣1时,函数取得最大值;当x=1时,函数取得最小值,则t的取值范围是( )
A.0<t≤2 B.0<t≤4 C.2≤t≤4 D.t≥2
10.如图,在平面直角坐标系中,Rt△AOB的一条直角边OB在x轴上,点A的坐标为(﹣6,4);Rt△COD中,∠COD=90°,OD=4,∠D=30°,连接BC,点M是BC中点,连接AM.将Rt△COD以点O为旋转中心按顺时针方向旋转,在旋转过程中,线段AM的最小值是( )
A.3 B.6﹣4
C.2﹣2 D.2
二、填空题(6小题,每题3分,共18分)
11.在平面直角坐标系中,若点P(2,﹣1)与点Q(﹣2,m)关于原点对称,则m的值是 .
12.已知是y关于x的二次函数,m= .
13.已知方程x2+x﹣2=0的两根分别为x1,x2,则的值为 .
14.将抛物线y=﹣x2先向右平移1个单位长度,再向上平移2个单位长度,则平移后抛物线的顶点坐标为 .
15.已知抛物线y=x2﹣6x+m与x轴有且只有一个交点,则m= .
16.如图,已知Rt△ABC中,∠ABC=90°,∠ACB=30°,斜边AC=4,点P是三角形内的一动点,则PA+PB+PC的最小值是 .
第II卷
2024—2025学年人教版数学九年级上册期末复习测试C卷
姓名:____________ 学号:____________准考证号:___________
题号 一 二 三 总分
17 18 19 20 21 22 23 24 25
得分
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.已知关于x的一元二次方程x2﹣(2m﹣1)x﹣3m2+m=0.
(1)求证:无论m为何值,方程总有实数根;
(2)若x1,x2是方程的两个实数根,且+=﹣,求m的值.
18.某中学开设足球、篮球、乒乓球、羽毛球、排球五项球类活动,为了解学生对这五项活动的喜爱情况,随机调查了m名学生(每名学生必选且只能选择这五项活动中的一项),并根据调查结果绘制了如图所示的两幅不完整的统计图,根据统计图提供的信息,解答下列问题:
(1)m= ,n= ,并补全条形统计图;
(2)在抽查的m名学生中,学校打算从喜欢羽毛球运动的甲、乙、丙、丁四人中选取2名参加区中学生羽毛球比赛,请用列表法或画树状图法求同时选中甲、丙的概率.
19.如图,将△ABC绕点C逆时针旋转90°得△DEC,其中点A,点B的对应点分别是点D,点E,点B落在DE上,延长AC交DE于点F,AB、DC交于点G.
(1)求证:AB⊥DE;
(2)求证:FB+BG=BC.
20.如图,在△ABC中,以AB为直径的⊙O交BC于点D,DE⊥AC,垂足为E.⊙O的两条弦FB,FD相交于点F,∠DAE=∠BFD.
(1)求证:DE是⊙O的切线;
(2)若∠C=30°,CD=2,求扇形OBD的面积.
21.国庆期间某旅游点一家商铺销售一批成本为每件50元的商品,规定销售单价不低于成本价,又不高于每件70元,销售量y(件)与销售单价x(元)的关系可以近似的看作一次函数(如图).
(1)请直接写出y关于x的函数表达式 ;
(2)设该商铺销售这批商品获得的总利润为w元,当销售单价为多少元时,可获得的总利润最大?最大总利润是多少?
22.如图,抛物线与直线y2=kx+c交于B(3,0),C(0,﹣3)两点,抛物线与x轴的另一个交点为A.
(1)b= ;c= ;k= ;
(2)关于x的不等式﹣x2+bx+c<kx+c的解集为 ;
(3)求△ABC的面积.
23.如图,AB是半径为5的⊙O的直径,C是的中点,连接CD交AB于点E,连接AC,AD,OC.
(1)求证:OC⊥AD.
(2)若BE=1,求AD的长.
(3)如图2,作CF⊥AB于点H,交AD于点F,射线CB交AD的延长线于点G,若OH=1,求AG的长.
24.已知二次函数y=x2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.
(1)求抛物线的解析式.
(2)抛物线的对称轴上有一动点P,求出PA+PD值最小时P点的坐标.
(3)在第三象限中的抛物线上是否存在一点Q,使△QAC的面积最大?若存在,求出Q点的坐标及△QAC面积的最大值;若不存在,说明理由.
25.已知抛物线l1:y=ax2+(2b+1)x+2b,直线l2:y=mx+n(0<m<n).
(1)若抛物线l1的对称轴为直线x=1,且经过点(﹣1,0),求该抛物线的解析式;
(2)在(1)的条件下,将抛物线l1图象x轴下方的部分沿x轴向上翻折,得到的新图象记作w,图象w与直线y=t+1恒有四个交点,从左到右四个交点依次记为A,B,C,D,是否存在以BC为直径的圆恰好过点M(1,1)?若存在,求出t的值;若不存在,请说明理由;
(3)若抛物线l1经过(s,﹣4),当a=1,﹣2<b<2时,对于任意实数x,满足ax2+(2b+1)x+2b≥﹣4恒成立;且当m≤x≤n时,恰好有,求直线l2的解析式.
同课章节目录
