2024—2025学年湘教版数学七年级上册期末复习测试B卷(无答案)
文档属性
| 名称 | 2024—2025学年湘教版数学七年级上册期末复习测试B卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 189.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-04 22:29:44 | ||
图片预览


文档简介
2024—2025学年湘教版数学七年级上册期末复习测试B卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.地球的表面积约为510000000km2,将510000000用科学记数法表示为( )
A.0.51×109 B.5.1×108 C.5.1×109 D.51×107
2.下面几何体中,是圆锥的为( )
A. B. C. D.
3.下列变形中,不正确的是( )
A.若a﹣3=b﹣3,则a=b B.若,则a=b
C.若a=b,则 D.若ac=bc,则a=b
4.解方程=1﹣,去分母后,结果正确的是( )
A.2(x﹣1)=1﹣(3x+1) B.2(x﹣1)=6﹣3x+1
C.2x﹣1=6﹣3x+1 D.2(x﹣1)=6﹣(3x+1)
5.已知|a﹣1|=5,则a的值为( )
A.6 B.﹣4 C.6或﹣4 D.﹣6或4
6.若方程(a﹣1)x|a|﹣1=5是关于x的一元一次方程,则a的值为( )
A.±1 B.2 C.±2 D.﹣1
7.今年我市有5万名学生参加中考,为了了解这些考生的数学成绩,教育部门抽取了2000名考生的数学成绩进行统计分析,在这个问题中,下列说法正确的是( )
A.2000名考生是总体的一个样本 B.每个考生是个体
C.这5万名学生的数学中考成绩的全体是总体 D.样本容量是2000名学生
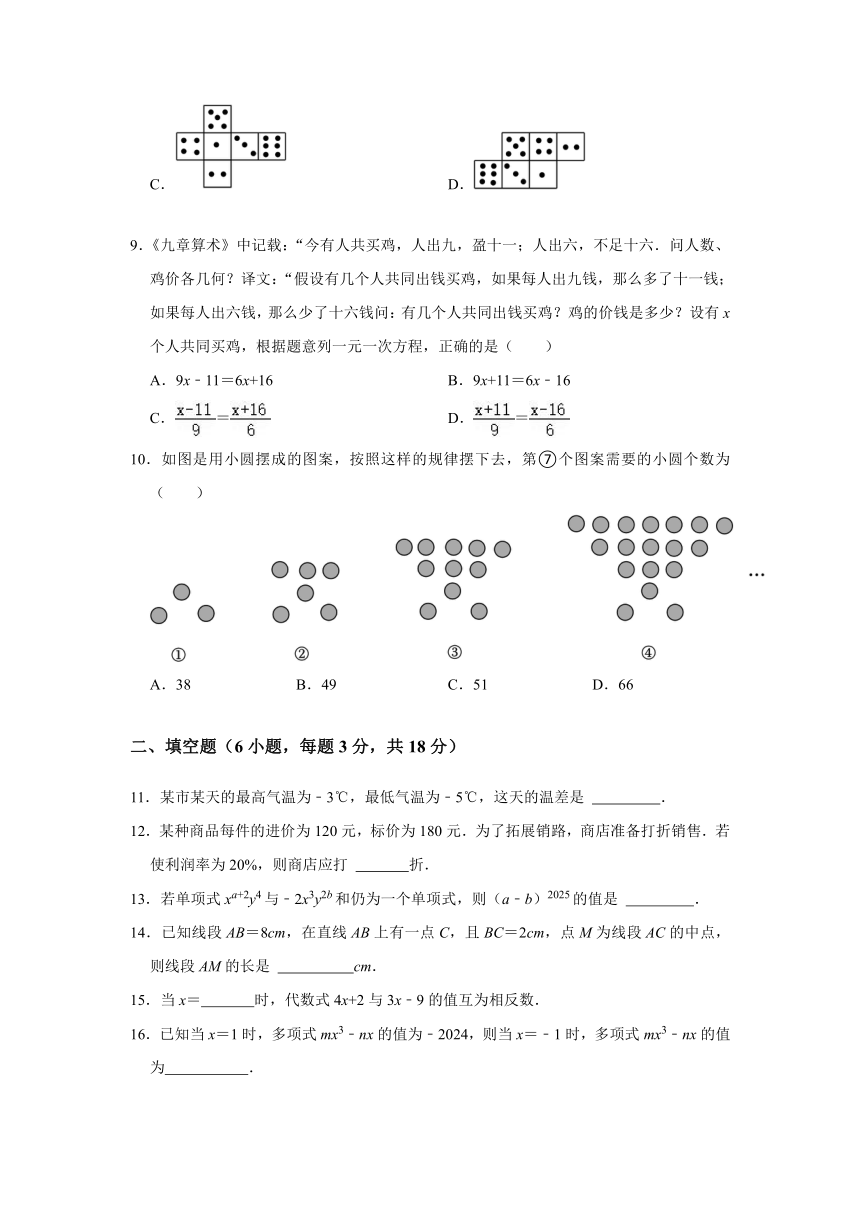
8.下列纸板中,可通过折叠做成正方体且每个对立面点数和为7的是( )
A. B.
C. D.
9.《九章算术》中记载:“今有人共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?译文:“假设有几个人共同出钱买鸡,如果每人出九钱,那么多了十一钱;如果每人出六钱,那么少了十六钱问:有几个人共同出钱买鸡?鸡的价钱是多少?设有x个人共同买鸡,根据题意列一元一次方程,正确的是( )
A.9x﹣11=6x+16 B.9x+11=6x﹣16
C.= D.=
10.如图是用小圆摆成的图案,按照这样的规律摆下去,第⑦个图案需要的小圆个数为( )
A.38 B.49 C.51 D.66
二、填空题(6小题,每题3分,共18分)
11.某市某天的最高气温为﹣3℃,最低气温为﹣5℃,这天的温差是 .
12.某种商品每件的进价为120元,标价为180元.为了拓展销路,商店准备打折销售.若使利润率为20%,则商店应打 折.
13.若单项式xa+2y4与﹣2x3y2b和仍为一个单项式,则(a﹣b)2025的值是 .
14.已知线段AB=8cm,在直线AB上有一点C,且BC=2cm,点M为线段AC的中点,则线段AM的长是 cm.
15.当x= 时,代数式4x+2与3x﹣9的值互为相反数.
16.已知当x=1时,多项式mx3﹣nx的值为﹣2024,则当x=﹣1时,多项式mx3﹣nx的值为 .
第II卷
2024—2025学年湘教版数学七年级上册期末复习测试B卷
姓名:____________ 学号:____________准考证号:___________
题号 一 二 三 总分
17 18 19 20 21 22 23 24 25
得分
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:
(1)﹣16+5﹣(﹣2);
(2)|﹣2|.
18.已知多项式3(ax2+x﹣y)﹣(3x2﹣bx+5y﹣1),其中x,y满足x﹣4y=1.
(1)若a=1,b=﹣1,将多项式化简并求值;
(2)若多项式的值与字母x的取值无关,求a,b的值.
19.a※b是规定的一种新运算法则:a※b=a2+ab,例如:3※(﹣2)=32+3×(﹣2)=3.
(1)求(﹣3)※5的值:
(2)若3※(2※x)=﹣4+x,求x的值.
20.某校为了解七年级600名学生双手垫排球的情况,从七年级学生中随机抽取部分学生进行双手垫排球测试,并对测试成绩进行统计分析,得到如下尚不完整的统计图和统计表:
垫球个数(n) 0≤n≤25 25<n≤35 35<n≤45 45<n≤55 55<n≤65
频数 6 9 21 a 9
所占百分比 b 15% 35% 25% 15%
请根据尚未完成的统计图表,解答下列问题:
(1)请直接写出a,b的值并补全频数分布直方图;
(2)若绘制“七年级学生双手垫排球测试成绩扇形统计图”,则测试成绩在35<n≤45个所对应扇形的圆心角的度数是 ;
(3)若双手垫排球个数超过45个为优秀,则该校七年级学生双手垫排球成绩优秀的约有多少人?
21.2024年1月日历排列如图所示,用“X”形的方式任意框五个数.
(1)若框住的5个数中,正中间的一个数为10,则这5个数的和为 .
(2)用式子表示“X”形框内五个数的和.
(3)“X”形框能否框住这样的5个数,使得它们的和等于120?若能,求出正中间的数;若不能,请说明理由.
22.有理数a,b,c在数轴上对应的点的位置如图所示.
(1)由图可得:|a| |b|(用“<”“>”“=”填空);
(2)由图可得:a﹣b 0,a+b 0,b﹣c 0(用“<”“>”“=”填空);
(3)结合(2)化简:|a﹣b|+|a+b|﹣|b﹣c|.
23.欧尚超市恰好用3200元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的与少10件,甲、乙两种商品的进价和售价如表:(注:每件商品获利=售价﹣进价).
甲 乙
进价(元/件) 20 30
售价(元/件) 25 40
(1)该商场购进甲、乙两种商品各多少件?
(2)该超市将购进的甲、乙两种商品全部卖完后一共可获得多少利润?
24.定义:如果两个一元一次方程的解互为相反数,我们就称这两个方程为“和谐方程”.
例如:方程2x=4和x+2=0为“和谐方程”.
(1)若关于x的方程3x+m=0与方程4x﹣2=x+10是“和谐方程”,求m的值;
(2)若“和谐方程”的两个解的差为4,其中一个解为n,求n的值;
(3)若无论m取任何有理数,关于x的方程+m(a、b为常数)与关于y的方程y+1=2y﹣2都是“和谐方程”,求ab的值.
25.定义:从一个角的顶点出发,在角的内部引两条射线,如果这两条射线所成的角等于这个角的一半,那么这两条射线所成的角叫做这个角的内半角.如图①所示,若∠COD=∠AOB,则∠COD是∠AOB的内半角.
(1)如图①所示,已知∠AOB=70°,∠AOC=15°,∠COD是∠AOB的内半角,则∠BOD= .
(2)如图②,已知∠AOB=63°,将∠AOB绕点O按顺时针方向旋转一个角度α(0<α<63°)至∠COD,当旋转的角度α为何值时,∠COB是∠AOD的内半角?
(3)已知∠AOB=30°,把一块含有30°角的三角板如图③叠放,将三角板绕顶点O以3°/秒的速度按顺时针方向旋转,如图④,问:在旋转一周的过程中,且射线OD始终在∠AOB的外部,射线OA,OB,OC,OD能否构成内半角?若能,请直接写出旋转的时间;若不能,请说明理由.
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.地球的表面积约为510000000km2,将510000000用科学记数法表示为( )
A.0.51×109 B.5.1×108 C.5.1×109 D.51×107
2.下面几何体中,是圆锥的为( )
A. B. C. D.
3.下列变形中,不正确的是( )
A.若a﹣3=b﹣3,则a=b B.若,则a=b
C.若a=b,则 D.若ac=bc,则a=b
4.解方程=1﹣,去分母后,结果正确的是( )
A.2(x﹣1)=1﹣(3x+1) B.2(x﹣1)=6﹣3x+1
C.2x﹣1=6﹣3x+1 D.2(x﹣1)=6﹣(3x+1)
5.已知|a﹣1|=5,则a的值为( )
A.6 B.﹣4 C.6或﹣4 D.﹣6或4
6.若方程(a﹣1)x|a|﹣1=5是关于x的一元一次方程,则a的值为( )
A.±1 B.2 C.±2 D.﹣1
7.今年我市有5万名学生参加中考,为了了解这些考生的数学成绩,教育部门抽取了2000名考生的数学成绩进行统计分析,在这个问题中,下列说法正确的是( )
A.2000名考生是总体的一个样本 B.每个考生是个体
C.这5万名学生的数学中考成绩的全体是总体 D.样本容量是2000名学生
8.下列纸板中,可通过折叠做成正方体且每个对立面点数和为7的是( )
A. B.
C. D.
9.《九章算术》中记载:“今有人共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?译文:“假设有几个人共同出钱买鸡,如果每人出九钱,那么多了十一钱;如果每人出六钱,那么少了十六钱问:有几个人共同出钱买鸡?鸡的价钱是多少?设有x个人共同买鸡,根据题意列一元一次方程,正确的是( )
A.9x﹣11=6x+16 B.9x+11=6x﹣16
C.= D.=
10.如图是用小圆摆成的图案,按照这样的规律摆下去,第⑦个图案需要的小圆个数为( )
A.38 B.49 C.51 D.66
二、填空题(6小题,每题3分,共18分)
11.某市某天的最高气温为﹣3℃,最低气温为﹣5℃,这天的温差是 .
12.某种商品每件的进价为120元,标价为180元.为了拓展销路,商店准备打折销售.若使利润率为20%,则商店应打 折.
13.若单项式xa+2y4与﹣2x3y2b和仍为一个单项式,则(a﹣b)2025的值是 .
14.已知线段AB=8cm,在直线AB上有一点C,且BC=2cm,点M为线段AC的中点,则线段AM的长是 cm.
15.当x= 时,代数式4x+2与3x﹣9的值互为相反数.
16.已知当x=1时,多项式mx3﹣nx的值为﹣2024,则当x=﹣1时,多项式mx3﹣nx的值为 .
第II卷
2024—2025学年湘教版数学七年级上册期末复习测试B卷
姓名:____________ 学号:____________准考证号:___________
题号 一 二 三 总分
17 18 19 20 21 22 23 24 25
得分
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:
(1)﹣16+5﹣(﹣2);
(2)|﹣2|.
18.已知多项式3(ax2+x﹣y)﹣(3x2﹣bx+5y﹣1),其中x,y满足x﹣4y=1.
(1)若a=1,b=﹣1,将多项式化简并求值;
(2)若多项式的值与字母x的取值无关,求a,b的值.
19.a※b是规定的一种新运算法则:a※b=a2+ab,例如:3※(﹣2)=32+3×(﹣2)=3.
(1)求(﹣3)※5的值:
(2)若3※(2※x)=﹣4+x,求x的值.
20.某校为了解七年级600名学生双手垫排球的情况,从七年级学生中随机抽取部分学生进行双手垫排球测试,并对测试成绩进行统计分析,得到如下尚不完整的统计图和统计表:
垫球个数(n) 0≤n≤25 25<n≤35 35<n≤45 45<n≤55 55<n≤65
频数 6 9 21 a 9
所占百分比 b 15% 35% 25% 15%
请根据尚未完成的统计图表,解答下列问题:
(1)请直接写出a,b的值并补全频数分布直方图;
(2)若绘制“七年级学生双手垫排球测试成绩扇形统计图”,则测试成绩在35<n≤45个所对应扇形的圆心角的度数是 ;
(3)若双手垫排球个数超过45个为优秀,则该校七年级学生双手垫排球成绩优秀的约有多少人?
21.2024年1月日历排列如图所示,用“X”形的方式任意框五个数.
(1)若框住的5个数中,正中间的一个数为10,则这5个数的和为 .
(2)用式子表示“X”形框内五个数的和.
(3)“X”形框能否框住这样的5个数,使得它们的和等于120?若能,求出正中间的数;若不能,请说明理由.
22.有理数a,b,c在数轴上对应的点的位置如图所示.
(1)由图可得:|a| |b|(用“<”“>”“=”填空);
(2)由图可得:a﹣b 0,a+b 0,b﹣c 0(用“<”“>”“=”填空);
(3)结合(2)化简:|a﹣b|+|a+b|﹣|b﹣c|.
23.欧尚超市恰好用3200元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的与少10件,甲、乙两种商品的进价和售价如表:(注:每件商品获利=售价﹣进价).
甲 乙
进价(元/件) 20 30
售价(元/件) 25 40
(1)该商场购进甲、乙两种商品各多少件?
(2)该超市将购进的甲、乙两种商品全部卖完后一共可获得多少利润?
24.定义:如果两个一元一次方程的解互为相反数,我们就称这两个方程为“和谐方程”.
例如:方程2x=4和x+2=0为“和谐方程”.
(1)若关于x的方程3x+m=0与方程4x﹣2=x+10是“和谐方程”,求m的值;
(2)若“和谐方程”的两个解的差为4,其中一个解为n,求n的值;
(3)若无论m取任何有理数,关于x的方程+m(a、b为常数)与关于y的方程y+1=2y﹣2都是“和谐方程”,求ab的值.
25.定义:从一个角的顶点出发,在角的内部引两条射线,如果这两条射线所成的角等于这个角的一半,那么这两条射线所成的角叫做这个角的内半角.如图①所示,若∠COD=∠AOB,则∠COD是∠AOB的内半角.
(1)如图①所示,已知∠AOB=70°,∠AOC=15°,∠COD是∠AOB的内半角,则∠BOD= .
(2)如图②,已知∠AOB=63°,将∠AOB绕点O按顺时针方向旋转一个角度α(0<α<63°)至∠COD,当旋转的角度α为何值时,∠COB是∠AOD的内半角?
(3)已知∠AOB=30°,把一块含有30°角的三角板如图③叠放,将三角板绕顶点O以3°/秒的速度按顺时针方向旋转,如图④,问:在旋转一周的过程中,且射线OD始终在∠AOB的外部,射线OA,OB,OC,OD能否构成内半角?若能,请直接写出旋转的时间;若不能,请说明理由.
同课章节目录
