2025年九年级中考数学二轮复习专题:二次函数中等腰三角形存在性问题(含详解)
文档属性
| 名称 | 2025年九年级中考数学二轮复习专题:二次函数中等腰三角形存在性问题(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-05 11:36:49 | ||
图片预览



文档简介
2025年九年级中考数学二轮复习专题:二次函数中等腰三角形存在性问题
1.如图,已知抛物线y=﹣x2+bx+c经过B(﹣3,0),C(0,3)两点,与x轴的另一个交点为A.
(1)求抛物线的解析式;
(2)在抛物线对称轴上找一点E,使得AE+CE的值最小,直接写出点E的坐标;
(3)设点P为x轴上的一个动点,是否存在使△BPC为等腰三角形的点P,若存在,直接写出点P的坐标;若不存在,说明理由.
2.如图,已知抛物线y=ax2+bx﹣2(a≠0)经过点A(﹣3,2),与y轴交于点B,其对称轴为直线,为y轴上一点,直线AC与抛物线交于另一点D.
(1)求抛物线的函数表达式;
(2)试在线段AD下方的抛物线上求一点E,使得△ADE的面积最大,并求出最大面积;
(3)在抛物线的对称轴上是否存在一点F,x轴上一点N,使得△DNF是等腰直角三角形?如果存在,求点F的坐标;如果不存在,请说明理由.
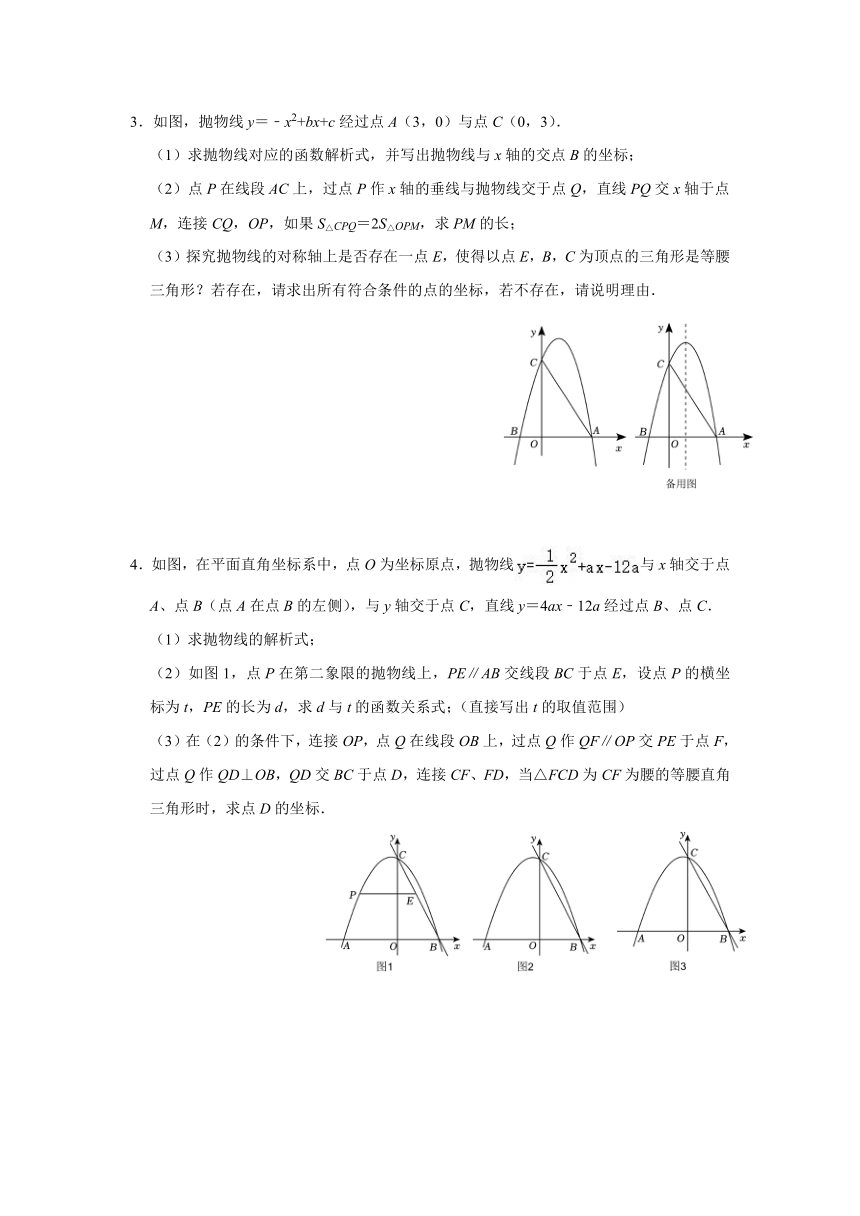
3.如图,抛物线y=﹣x2+bx+c经过点A(3,0)与点C(0,3).
(1)求抛物线对应的函数解析式,并写出抛物线与x轴的交点B的坐标;
(2)点P在线段AC上,过点P作x轴的垂线与抛物线交于点Q,直线PQ交x轴于点M,连接CQ,OP,如果S△CPQ=2S△OPM,求PM的长;
(3)探究抛物线的对称轴上是否存在一点E,使得以点E,B,C为顶点的三角形是等腰三角形?若存在,请求出所有符合条件的点的坐标,若不存在,请说明理由.
4.如图,在平面直角坐标系中,点O为坐标原点,抛物线与x轴交于点A、点B(点A在点B的左侧),与y轴交于点C,直线y=4ax﹣12a经过点B、点C.
(1)求抛物线的解析式;
(2)如图1,点P在第二象限的抛物线上,PE∥AB交线段BC于点E,设点P的横坐标为t,PE的长为d,求d与t的函数关系式;(直接写出t的取值范围)
(3)在(2)的条件下,连接OP,点Q在线段OB上,过点Q作QF∥OP交PE于点F,过点Q作QD⊥OB,QD交BC于点D,连接CF、FD,当△FCD为CF为腰的等腰直角三角形时,求点D的坐标.
5.如图,关于x的二次函数y=x2+bx+c的图象与x轴相交于点A(1,0)和点B(3,0),与y轴相交于点C.
(1)求二次函数的表达式和线段BC的长;
(2)在抛物线对称轴上找一点P,使△PBC为等腰三角形?直接写出点P的坐标.
6.如图,抛物线y=x2+bx+c与x轴交于A(﹣2,0),B(4,0)两点,与y轴交于点C,连接AC、BC,点P是第四象限内抛物线上的一个动点,点P的横坐标为m,过点P作PM⊥x轴,垂足为点M,PM交BC于点Q.
(1)求抛物线的解析式;
(2)运动过程中是否存在点P,使线段PQ的值最大?若存在,请求出这个最大值并求出此时P点的坐标;若不存在,请说明理由;
(3)试探究在点P的过程中,是否存在这样的点Q,使得以A、C、Q为顶点的三角形是等腰三角形?若存在,请求出此时点Q的坐标;若不存在,请说明.
7.如图,已知抛物线y=ax2+bx﹣3的图象与x轴交于点A(1,0)和B(3,0),与y轴交于点C,点D是抛物线的顶点,对称轴与x轴交于点E.
(1)求抛物线的解析式;
(2)如图1,在抛物线的对称轴DE上求作一点M,使△AMC的周长最小,并求出点M的坐标和周长的最小值;
(3)如图2,点P是x轴上动点,过点P作x轴的垂线分别交抛物线和直线BC于点F、G.设点P的横坐标为m,是否存在点P,使△FCG是以FG为腰的等腰三角形?若存在,直接写出m的值;若不存在,请说明理由.
8.如图,抛物线y=ax2+3x+c(a≠0)与x轴交于点A(﹣2,0)和点B,与y轴交于点C(0,8),点P为直线BC上方抛物线上的动点,连接CP,PB,直线BC与抛物线的对称轴l交于点E.
(1)求抛物线的解析式;
(2)求△BCP的面积最大值;
(3)点M是抛物线的对称轴l上一动点.是否存在点M,使得△BEM为等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
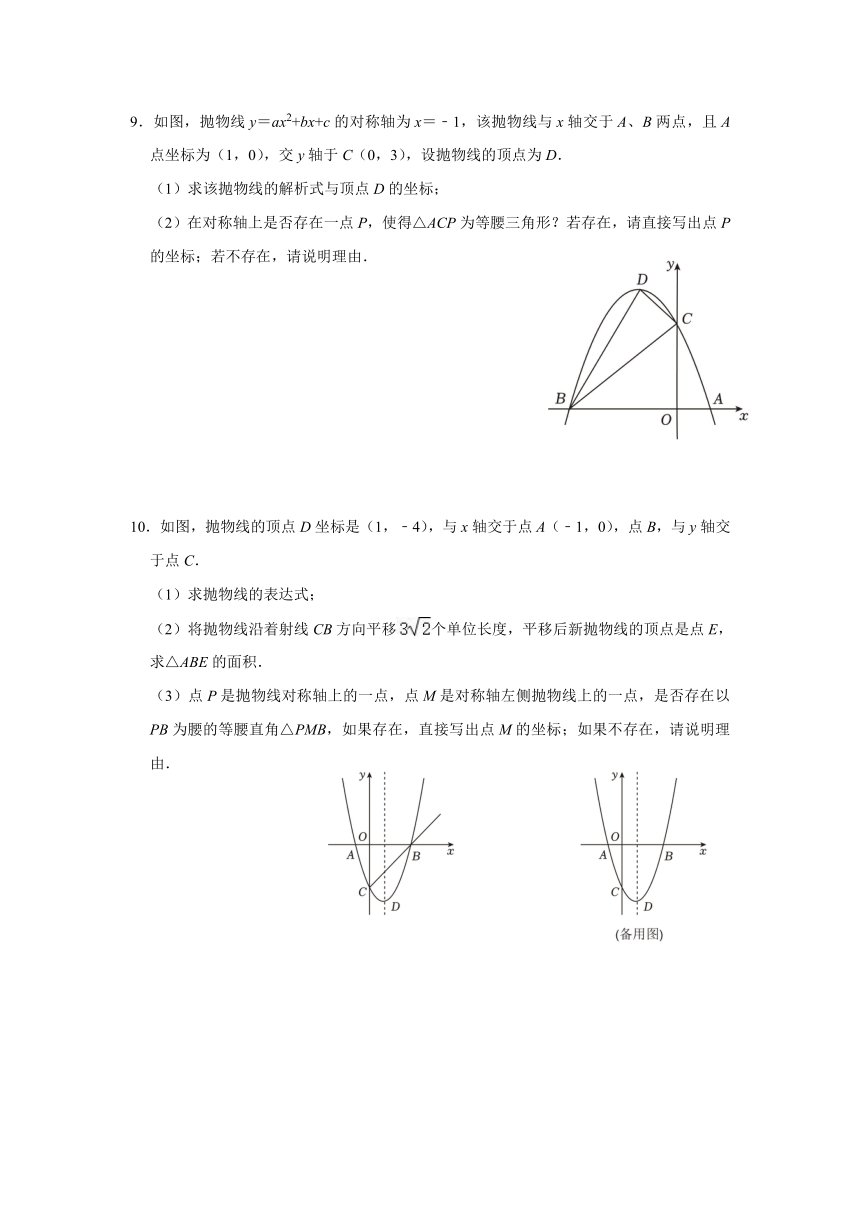
9.如图,抛物线y=ax2+bx+c的对称轴为x=﹣1,该抛物线与x轴交于A、B两点,且A点坐标为(1,0),交y轴于C(0,3),设抛物线的顶点为D.
(1)求该抛物线的解析式与顶点D的坐标;
(2)在对称轴上是否存在一点P,使得△ACP为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
10.如图,抛物线的顶点D坐标是(1,﹣4),与x轴交于点A(﹣1,0),点B,与y轴交于点C.
(1)求抛物线的表达式;
(2)将抛物线沿着射线CB方向平移个单位长度,平移后新抛物线的顶点是点E,求△ABE的面积.
(3)点P是抛物线对称轴上的一点,点M是对称轴左侧抛物线上的一点,是否存在以PB为腰的等腰直角△PMB,如果存在,直接写出点M的坐标;如果不存在,请说明理由.
11.如图,在平面直角坐标系中,抛物线y=ax2﹣3x+c与x轴交于点A(﹣4,0)和点C,与y轴交于点B(0,4),点P是抛物线上一动点.
(1)求抛物线的解析式;
(2)动点P在抛物线上,且在直线AB上方,求△ABP面积的最大值及此时点P的坐标;
(3)在(2)的条件下,点F为抛物线顶点,Q为抛物线的对称轴上任意一点,若△PFQ是等腰三角形,求出所有符合条件的点Q的坐标.
12.如图,抛物线y=ax2+bx+c的对称轴为直线,且经过A(﹣4,0),C(0,2)两点,与x轴交于另一点B.
(1)求抛物线的解析式;
(2)若点P为直线AC上方的抛物线上的一点,连接PA,PC,求△PAC的面积的最大值,并求出此时点P的坐标;
(3)在对称轴上是否存在点Q,使△QBC为等腰三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
13.如图,二次函数y=﹣x2+(k﹣1)x+4的图象与y轴交于点A与x轴的负半轴交于点B,且△AOB的面积为6.
(1)求A,B两点的坐标;
(2)求该二次函数的表达式;
(3)如果点p在坐标轴上,且△ABP是等腰三角形,直接写出p点坐标.
14.如图,二次函数的图象的顶点C的横坐标为﹣1,直线y=﹣x+n与该二次函数的图象交于A,B两点,其中点A的坐标为(﹣3,2),点B在y轴上.
(1)求n的值及二次函数的表达式.
(2)求△ABC的面积.
(3)在该二次函数的对称轴上是否存在点Q,使得△ABQ是以AB为腰的等腰三角形?若存在,请求出符合条件的Q点的坐标;若不存在,请说明理由.
15.综合与探究
如图,抛物线y=x2﹣3x﹣4与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,连接BC.若点P在线段BC上运动(点P不与点B,C重合),过点P作x轴的垂线,交抛物线于点E,交x轴于点F.设点P的横坐标为m.
(1)求点A,B,C的坐标,并直接写出直线BC的函数解析式.
(2)若PF=2PE,求m的值.
(3)在点P的运动过程中,是否存在m使得△CPE为等腰直角三角形?若存在,请直接写出m的值;若不存在,请说明理由.
16.如图,二次函数y=ax2+bx+c的图象交x轴于A(﹣2,0),B(1,0),交y轴于C(0,2).
(1)求二次函数的解析式;
(2)连接AC,在直线AC上方的抛物线上是否存在点N,使△NAC的面积最大,若存在,求出这个最大值及此时点N的坐标,若不存在,说明理由;
(3)若点M在x轴上,是否存在点M,使以B、C、M为顶点的三角形是等腰三角形,若存在,直接写出点M的坐标;若不存在,说明理由.
参考答案
1.【解答】解:(1)已知抛物线y=﹣x2+bx+c经过B(﹣3,0),C(0,3)两点,将点B,点C的坐标代入得:
,
解得,
故抛物线的解析式为y=﹣x2﹣2x+3;
(2)∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴抛物线的对称轴为直线x=﹣1,
∵点A、B关于直线l对称,
∴BC与对称轴l的交点即为点E,如图,
则此时AE+CE=BE+CE=BC为最小,
设直线BC的解析式为y=mx+n,将点B,点C的坐标代入得:
,
解得,
∴直线BC的解析式为y=x+3;
当x=﹣1时,y=x+3=2,
∴点E(﹣1,2);
(3)∵B(﹣3,0),C(0,3),
∴OB=OC=3,
∴,
当B为顶角的顶点时,
则,
∴点P的坐标为或;
当C为顶角的顶点时,
则PC=BC,
∴点P与点B关于y轴对称,
∴点P的坐标为(3,0);
当BC为底边时,
则PC=PB,即点P在线段BC的垂直平分线上,
∴点P的坐标为(0,0);
综上,点P的坐标为(0,0)或(3,0)或或.
【点评】主要属于二次函数综合题,主要考查了二次函数的图象与性质,等定系数法求函数解析式,解答本题的关键是利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度.
2.【解答】解:(1)由题意得:,
解得:
∴y=x2﹣x﹣2;
(2)由点A、C的坐标得,直线AC的表达式为:y=﹣x+,
联立上式和抛物线的表达式得:﹣x+=x2﹣x﹣2,
解得:x=﹣3(舍去)或5,
∴D(5,﹣2),
过点E作EG∥y轴交AC于点G,
设E(x,x2﹣x﹣2),则G(x,﹣x+),
∴EG=﹣x+﹣x2+x+2,
∴S△ADE=×8(﹣x+﹣x2+x+2)=﹣(x﹣1)2+,
∵﹣3<x<5,
∴当x=1时,△ADE的面积最大为,
此时E(1,﹣);
(3)存在一点F,x轴上一点N使得△DNF是等腰直角三角形,理由如下:
∵抛物线对称轴为直线x=,
设N(x,0),
如图1:当∠FND=90°,NF=DN时,过点N作HI⊥x轴,过点F作FH⊥HI交于H点,过点D作DI⊥HI交于点I,
∵∠FND=90°,
∴∠FNH+∠DNI=90°,
∵∠FNH+∠HFN=90°,
∴∠DNI=∠HFN,
∴△FHN≌△NID(AAS),
∴FH=NI=2,HN=ID,
∴|x﹣|=2,
解得x=或x=,
则DI=5﹣=或DI=5﹣=,
则F(,)或(,);
如图2,当∠FDN=90°,DF=DN时,过点K作KL∥x轴交对称轴于点K,过点N作NL⊥KL交于L点,
同理可证△FKD≌△DLN(AAS),
∴NL=KD=2,DL=FK,
∵KD=5﹣=≠2,
∴此情况不存在;
如图3,当∠NFK=90°,NF=FD,过F点作TS∥x轴,过点N作TN⊥TS交于点T,过点D作DS⊥TS交于点S,
同理可证△FNT≌△DFS(AAS),
∴NT=SF,DS=TF,
∴NT=,
∴F(,﹣);
综上所述:F点坐标为(,)或(,)或(,﹣).
【点评】本题考查二次函数的图象及性质,熟练掌握二次函数的图象及性质,等腰直角三角形的性质,三角形全等的判定及性质,勾股定理是解题的关键.
3.【解答】解:(1)将A(3,0),点C(0,3)代入抛物线y=﹣x2+bx+c得:
,
解得,
∴抛物线对应的函数解析式为y=﹣x2+2x+3,
令y=0,则﹣x2+2x+3=0,
解得x1=﹣1,x2=3,
∴抛物线与x轴的交点B的坐标为(﹣1,0);
(2)设点P的横坐标为m,则Q(m,﹣m2+2m+3),M(m,0),
设直线AC的解析式为y=kx+n,
将A(3,0),C(0,3)代入得,
解得,
∴直线AC的解析式为y=﹣x+3,
∴P(m,﹣m+3),
∴PQ=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m,PM=﹣m+3,
∵S△CPQ=2S△OPM,
∴PQ OM=2×OM PM,
∴PQ=2PM,
即﹣m2+3m=2(﹣m+3),
解得m=2或3(舍去),
∴PM=﹣m+3=1;
(3)如图:
∵y=﹣x2+2x+3,
∴抛物线的对称轴为x=﹣=1,
设点E的坐标为(1,a),
∵B(﹣1,0),C(0,3),
∴BC2=12+32=10,
BE2=22+a2=4+a2,
CE2=12+(a﹣3)2=a2﹣6a+10,
当BC=BE时,4+a2=10,
解得a=±,
∴点E的坐标为(1,)或(1,﹣);
当BC=CE时,a2﹣6a+10=10,
解得a=0或6(此时,点B、C、E在同一直线上,舍去),
∴点E的坐标为(1,0);
当CE=BE时,4+a2=a2﹣6a+10,
解得a=1,
∴点E的坐标为(1,1);
综上,存在,点E的坐标为(1,)或(1,﹣)或(1,0)或(1,1).
【点评】本题是二次函数综合题,考查了抛物线与x轴的交点,二次函数图象和性质,待定系数法求函数解析式,用点的坐标表示线段长度,等腰三角形的性质等知识,关键是对二次函数性质的掌握和运用以及分类思想的运用.
4.【解答】解:(1)在直线y=4ax﹣12a中,
当y=0时,4ax﹣12a=0,
∴x=3,
∴B的坐标为(3,0),
把点B的坐标(3,0)代入抛物线中得:﹣×9+3a﹣12a=0,
∴a=﹣,
∴抛物线的解析式为:y=﹣x2﹣x+6;
(2)由(1)得:C(0,6),
当y=0时,﹣x2﹣x+6=0,
解得:x1=3,x2=﹣4,
∴A的坐标为(﹣4,0),
设BC的解析式为:y=kx+n,
∴,
解得:,
∴BC的解析式为:y=﹣2x+6,
设点E的坐标为(x,﹣2x+6),
∵点P的横坐标为t,
∴P(t,﹣t2﹣t+6),
∵PE∥x轴,
∴﹣2x+6=﹣t2﹣t+6,
∴x=t2+t,
∴d=t2+t﹣t=t2﹣t(﹣4<t<0);
(3)如图3,延长QD,PE交于点G,
设点D的坐标为(m,﹣2m+6),则Q(m,0),
∵OP∥FQ,PE∥AB,
∴四边形POQF是平行四边形,
∴PF=OQ=m,
∵DQ⊥x轴,PE∥x轴,
∴∠G=90°,
∵△CFD是以CF为腰的等腰直角三角形,
∴CF=DF,∠CFD=90°,
∴∠CFH+∠DFG=90°,
∵∠CHF=∠CFH+∠FCH=90°,
∴∠DFG=∠FCH,
∴△CFH≌△FDG(AAS),
∴FH=DG,CH=FG,
∴,
解①得:t2+3t=0,
∴t1=0(舍),t2=﹣3,
把t=﹣3代入②中得:3﹣m=﹣++6﹣(﹣2m+6),
∴m=2,
∴D(2,2).
【点评】本题为二次函数的综合题,涉及待定系数法,函数与方程,三角形全等的性质和判定,等腰直角三角形的性质,平行四边形的性质和判定,坐标与图形的性质等知识点.在(1)中求出B的坐标是解题的关键,在(2)中求得直线BC解析式是解题的关键,在(3)证明△CFH≌△FDG是解题的关键.本题考查知识点较多,计算量较大,综合性较强.
5.【解答】解:(1)把A(1,0)和C(0,3)代入y=x2+bx+c,,
解得:,
∴二次函数的表达式为:y=x2﹣4x+3;
令抛物线y=0,则x2﹣4x+3=0,
解得x=1或x=3,
根据题意:B(3,0),
∵C(0,3),
则BC=3;
(2)存在.
理由:∵BC=3,
设点P(2,m),
由点P、B、C的坐标得,PB2=1+m2,BC=18,PC2=4+(m﹣3)2,
当PB=BC时,
则1+m2=18,则m=±,即点P(2,1±)
当PB=PC或BC=PC时,
同理可得:18=4+(m﹣3)2或1+m2=4+(m﹣3)2,
解得:m=2或3±,
即点P(2,2)或(2,3±),
综上,P(2,1±)或(2,2)或(2,3±).
【点评】本题是二次函数的综合题型,其中涉及到运用待定系数法求二次函数,等腰三角形的性质,轴对称的性质等知识,运用数形结合、分类讨论思想是解题的关键.
6.【解答】解:(1)把A(﹣2,0),B(4,0)代入y=x2+bx+c得,,
解得,
∴抛物线的解析式为y=x2﹣2x﹣8;
(2)存在,
∵抛物线y=x2+bx+c与y轴交于点C,
∴C(0,﹣8),
设直线BC的解析式为y=kx+n,
∴,
解得,
∴直线BC的解析式为y=2x﹣8,
∵点P的横坐标为m,过点P作PM⊥x轴,
∴P(m,m2﹣2m﹣8),Q(m,2m﹣8),
∴PQ=2m﹣8﹣(m2﹣2m﹣8)=﹣m2+4m=﹣(m﹣2)2+4,
∴当m=2时,线段PQ的值最大,这个最大值为4,
此时P点的坐标为(2,﹣8);
(3)由(2)直线BC的解析式为y=2x﹣8,
设Q(m,2m﹣8)(0<m<4),
当CQ=CA时,m2+(2m﹣8+8)2=68,
解得m1=,m2=﹣(舍去);
∴Q(,﹣8),
当AQ=AC时,(m+2)2+(2m﹣8)2=68,
解得:m1=(舍去),m2=0(舍去);
当QA=QC时,(m+2)2+(2m﹣8)2=m2+(2m)2,
解得m=,
∴Q(,﹣).
综上所述,满足条件的Q点坐标为(,﹣8)或(,﹣).
【点评】本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和等腰三角形的性质;会利用待定系数法求函数解析式;理解坐标与图形性质,会利用勾股定理表示线段之间的关系;会运用分类讨论的思想解决数学问题.
7.【解答】解:(1)已知抛物线y=ax2+bx﹣3的图象与x轴交于点A(1,0)和B(3,0),将点A、B的坐标代入得:
,
解得,
∴抛物线的解析式为y=﹣x2+4x﹣3;
(2)如图,连接BC交DE于点M,此时MA+MC最小,
又∵AC是定值,所以此时△AMC的周长最小.
令x=0时,则有y=﹣3,即C(0,﹣3),
∴OB=OC=3,OA=1,
∴;
同理,
∴此时△AMC的周长=;
∵DE是抛物线的对称轴,抛物线与x轴交点A(1,0)和B(3,0),
∴AE=BE=1,对称轴为x=2,
由OB=OC,∠BOC=90°得∠OBC=45°,
∴EB=EM=1,
又∵点M在第四象限,且在抛物线的对称轴上,
∴M(2,﹣1);
(3)存在点P,使△FCG是以FG为腰的等腰三角形;m=4或或;理由如下:
设直线BC的解析式为y=kx+b,把点B、C坐标代入得:
,
解得:,
∴直线BC的解析式为y=x﹣3,
∵点P的横坐标为m,
∴点F(m,﹣m2+4m﹣3),点G(m,m﹣3),
则FG2=(m﹣m)2+(﹣m2+4m﹣3﹣m+3)2=(﹣m2+3m)2,CF2=(m2﹣4m)2+m2,GC2=(m﹣0)2+(m﹣3+3)2=2m2,
当FG=FC时,则(﹣m2+3m)2=(m2﹣4m)2+m2,
解得m=0(舍去)或4;
当FG=CG时,则(﹣m2+3m)2=2m2,
解得m=0(舍去)或;
综上,存在点P,使△FCG是以FG为腰的等腰三角形;m=4或或.
【点评】本题考查的是二次函数综合运用,涉及到一次函数的性质、点的对称性、等腰三角形的性质等,其中(3),要注意分类求解,避免遗漏.
8.【解答】解:(1)将A(﹣2,0),C(0,8)代入y=ax2+3x+c,得:
,
解得,
∴;
(2)令y=0,则,
解得x=﹣2或x=8,
∴B(8,0),
设直线BC的解析式为y=kx+b,代入得:
,
解得,
∴y=﹣x+8,
过点P作PG∥y轴交BC于G,
设,则G(t,﹣t+8),
∴,
∴,
∴当t=4时,△BCP的面积有最大值,最大值为32;
(3)存在点M,使得△BEM为等腰三角形,理由如下:
∵,
∴抛物线的对称轴为直线x=3,
∴E(3,5),设M(3,m),
∴,,EM=|m﹣5|,
当BE=BM时,,
解得m=5(舍)或m=﹣5,
∴M(3,﹣5);
当BE=EM时,,
解得或,
∴或;
当BM=EM时,,
解得m=0,
∴M(3,0);
综上所述:M点坐标为(3,0)或(3,﹣5)或或.
【点评】本题考查了二次函数综合,待定系数法求二次函数解析式,二次函数综合﹣面积问题以及特殊三角形问题,熟练掌握二次函数的性质是解本题的关键.
9.【解答】解:(1)点A(1,0)关于x=﹣1的对称点B(﹣3,0),
设过A(1,0)、B(﹣3,0)的抛物线为y=a(x﹣1)(x+3),
该抛物线又过C(0,3),则有:3=﹣3a,解得a=﹣1,
即y=﹣(x+1)2+4=﹣x2﹣2x+3,顶点D为(﹣1,4);
(2)在对称轴上存在一点P,使得△ACP为等腰三角形;点P的坐标为(﹣1,1)或(﹣1,)或(﹣1,)或(﹣1,0).理由如下:
设P(﹣1,t),
∵A(1,0),C(0,3),
∴AP2=(1+1)2+t2=4+t2,CP2=12+(t﹣3)2=t2﹣6t+10,AC2=12+32=10,
∵△APC为等腰三角形,
∴有AP=CP、AP=AC和CP=AC三种情况,
①当AP=CP时,则有AP2=CP2,即4+t2=t2﹣6t+10,
解得t=1,
此时P(﹣1,1);
②当AP=AC时,则有AP2=AC2,即4+t2=10,
解得t=,
此时P(﹣1,)或(﹣1,);
③当CP=AC时,则有CP2=AC2,即t2﹣6t+10=10,
解得t=0或t=6,
此时P(﹣1,0)或P(﹣1,6),
设直线AC解析式为y=kx+b,将点A,点C的坐标代入得:
,
解得:,
∴直线AC解析式为y=﹣3x+3,
当x=﹣1时y=6,则P(﹣1,6)在直线AC上,
综上,在对称轴上存在一点P,使得△ACP为等腰三角形;点P的坐标为(﹣1,1)或(﹣1,)或(﹣1,)或(﹣1,0).
【点评】本题属于二次函数综合题,主要考查了二次函数的综合应用,待定系数法求解析式,等腰三角形的性质,勾股定理,解答本题的关键是熟练掌握二次函数的图象与性质.
10.【解答】解:(1)∵抛物线的顶点D的坐标为(1,﹣4),
∴设抛物线的函数关系式为y=a(x﹣1)2﹣4,
把点A(﹣1,0)代入得:0=a(﹣1﹣1)2﹣4,
解得:a=1,
∴抛物线的函数关系式为y=(x﹣1)2﹣4,即y=x2﹣2x﹣3;
(2)当x=0时,y=3,
∴C(0,﹣3),
∵顶点D坐标是(1,﹣4),
∴对称轴是:直线x=1,
∵抛物线与x轴交于点A(﹣1,0),
∴B(3,0),
∴OB=OC=3,
∵∠BOC=90°,
∴△BOC是等腰直角三角形,
∵将抛物线沿着射线CB方向平移个单位长度,
∴将抛物线向上平移3个单位,再向右平移3个单位,得到的解析式为:y=(x﹣1﹣3)2﹣4+3,即y=(x﹣4)2﹣1,
∴平移后新抛物线的顶点是点E的坐标为(4,﹣1),如图1,
∴△ABE的面积=×4×1=2;
(3)点P是抛物线对称轴上的一点,点M是对称轴左侧抛物线上的一点,当△PMB是以PB为腰的等腰直角三角形时,分以下几种情况讨论:
①当∠BPM=90°时,PM=PB,如图2,
∴M点与A点重合,
∴M(﹣1,0);
②当∠PBM=90°时,PB=BM,
如图3,当P点在M点上方时,过点B作x轴的垂线GH,过点P作PH⊥GB于点H,过点M作MG⊥HG于点G,
∵∠PBM=90°,
∴∠PBH+∠MBG=90°,
∵∠H=∠PBH+∠BPH=90°,
∴∠MBG=∠BPH,
∵BP=BM,∠H=∠G=90°,
∴△BPH≌△MBG(AAS),
∴BH=MG,PH=BG=2,
设P(1,t),则M(3﹣t,﹣2),
∴﹣2=(3﹣t)2﹣2(3﹣t)﹣3,
解得:t1=2+,t2=2﹣,
∴点M的坐标为(1﹣,﹣2)或(1+,﹣2),
∵M点在对称轴的左侧,
∴M点的坐标为(1﹣,﹣2);
③如图4,当P点在M点下方时,PB=PM,过点B作TS⊥x轴,过点M作MT⊥TS于T,过点P作PS⊥TS于S,
∵∠PBM=90°,
∴∠PBS+∠MBT=90°,
∵∠PBS+∠BPS=90°,
∴∠MBT=∠BPS,
∵BP=BM,∠T=∠S=90°,
∴△BPS≌△MBT(AAS),
∴BS=MT,PS=BT=2,
设P(1,t),则M(3+t,2),
∴2=(3+t)2﹣2(3+t)﹣3,
解得:t1=﹣2+,t2=﹣2﹣,
∴点M的坐标为(1﹣,2)或(1+,2),
∵M点在对称轴的左侧,
∴M点的坐标为(1﹣,﹣2);
综上所述,点M的坐标为(﹣1,0)或(1﹣,﹣2)或(1﹣,﹣2).
【点评】本题考查了二次函数的综合问题,待定系数法求二次函数关系式,全等三角形的性质和判定,等腰直角三角形的性质和判定,平移的原则等知识,正确作辅助线构建全等三角形,并注意用分类讨论的思想解决问题.
11.【解答】解:(1)抛物线y=ax2﹣3x+c与x轴交于点A(﹣4,0)和点C,与y轴交于点B(0,4),将点A,点B的坐标代入得:
,
解得:,
∴抛物线的解析式为y=﹣x2﹣3x+4;
(2)设直线AB的解析式为y=kx+b,将点A,点B的坐标代入得:
,
解得:,
∴直线AB的解析式为y=x+4,
过点P作x轴的垂线交AB于点H,如图:
设P(x,﹣x2﹣3x+4),
∴H(x,x+4),
∴PH=﹣x2﹣3x+4﹣(x+4)=﹣x2﹣4x,
∵△ABP面积=×PH×AO,
∴S△ABP=×(﹣x2﹣4x)×4=﹣2x2﹣8x=﹣2(x+2)2+8,
∴当x=﹣2时,△ABP面积最大值为8,
此时P(﹣2,6);
(3)抛物线整理得:y=﹣x2﹣3x+4=,
∴顶点F的坐标为,对称轴为直线,
设点Q的坐标为,
∴QF2=,PF2==,PQ2=,
当QF=PF时,则=,
解得:,,
∴此时点Q的坐标为:,;
当QF=PQ时,则=,
解得:,
∴点Q的坐标为:;
当PQ=PF时,=,
解得:m1=,m2=,
当m=时,P、Q重合,不合题意,舍去,
∴此时点Q的坐标为(﹣,);
综上所述,点Q的坐标为(,),(﹣,),(﹣,),(,).
【点评】本题属于二次函数综合题,主要考查二次函数的图象与性质,一次函数的图象与性质,待定系数法求函数解析式,等腰三角形的定义,熟练掌握二次函数的性质是解题的关键.
12.【解答】解:(1)抛物线y=ax2+bx+c的对称轴为直线,且经过A(﹣4,0),C(0,2)两点,与x轴交于另一点B.
由抛物线的对称性可知:点A与点B关于直线对称,
∴点B的坐标为(1,0),
设抛物线解析式为y=a(x+4)(x﹣1),把点C的坐标代入得:
2=﹣4a,
解得:,
∴;
(2)点P为直线AC上方的抛物线上的一点,设,
如图,过点P作PQ⊥x轴交AC于点Q,
设直线AC的解析式为y=kx+b1,将A(﹣4,0),C(0,2)代入得:
,
解得:,
∴直线AC的解析式为y=,
∴Q(m,m+2),
∴PQ=m+2﹣(m+2)=﹣2m,
∴S△PAC=PQ×4=2PQ=﹣m2﹣4m=﹣(m+2)2+4,
∴当m=﹣2时,S△PAC的最大值是4,此时P(﹣2,3).
(3)设点,
∵B(1,0),C(0,2),
当QB=QC时,,
解得:q=0,即;
当QB=BC时,,该方程无解;
当QC=BC时,,
解得:,即或.
综上,当点Q的坐标为或或.
【点评】本题属于二次函数综合题,主要考查了求二次函数解析式、二次函数与面积综合、二次函数与几何综合等知识点,掌握分类讨论思想成为解题的关键.
13.【解答】解:(1)∵二次函数y=﹣x2+(k﹣1)x+4的图象与y轴交于点A,
∴令x=0,得y=4,即A(0,4),OA=4.
∵△AOB的面积为6,
∴,
∵OA=4,
∴OB=3,
∴B(﹣3,0);
(2)∵二次函数y=﹣x2+(k﹣1)x+4的图象与x轴的负半轴交于点B,
又∵B(﹣3,0),
∴﹣(﹣3)2+(﹣3)(k﹣1)+4=0,
解得,
故二次函数解析式为;
(3)∵A(0,4),B(﹣3,0),
∴OA=4,OB=3,
∵∠BOA=90°,
∴.
①如图1,当AB=AP,P在x轴上时,
∵AB=AP,AO⊥BP,
∴OB=OP=3,
∴P(3,0);
②如图2,当AB=AP,P在y轴负半轴上时,
∵AB=5,AB=AP,
∴AP=5.
∵OA=4,
∴OP=AP﹣OA=1,
∴P(0,﹣1).
③同理,当AB=AP,P在y轴正半轴上时,
∵AB=5,AB=AP,
∴AP=5.
∵OA=4,
∴OP=AP+OA=9,
∴P(0,9);
④如图3,当BA=BP,P在x轴负半轴上时,
∵AB=5,AB=BP,
∴BP=5.
∵OB=3,
∴OP=OB+BP=3+5=8,
∴P(﹣8,0).
⑤如图4,当BA=BP,P在y轴负半轴上时,
∵AB=BP,BO⊥AP,
∴OA=OP=4,
∴P(0,﹣4).
⑥如图5,当BA=BP,P在x轴正半轴上时,
∵AB=5,AB=BP,
∴BP=5.
∵OB=3,
∴OP=PB﹣OB=5﹣3=2,
∴P(2,0).
⑦如图6,作AB的垂直平分线交y轴于点P1,交x轴于点P2,则有P1A=BP1,P2A=BP2,连接P1B,P2A.
∵A(0,4),B(﹣3,0),
∴OA=4,OB=3
设AP1=x,则P1B=AP1=x,OP1=OA﹣AP1=4﹣x,
在Rt△BOP1中,∠BOP1=90°,
∴,即32+(4﹣x)2=x2,
解得,即,.
∴,
同理,设OP2=y,则AP2=P2B=OP2+OB=y+3,OA=4,
在Rt△AOP2中,∠AOP2=90°,
∴,即42+y2=(y+3)2,
解得,即,
∴,
综上,符合题意的P点坐标为:(3,0),(0,﹣1),(0,9),(﹣8,0),(0,﹣4),(2,0),,.
【点评】本题属于二次函数综合题,主要考查了二次函数的图象与性质,等腰三角形的性质,熟练掌握二次函数相关性质是解题的关键.
14.【解答】解:(1)∵直线y=﹣x+n过点A(﹣3,2),
∴2=3+n,
解得n=﹣1,
∴y=﹣x﹣1.
令x=0,则y=﹣1,
∴点B(0,﹣1).
设二次函数的表达式为y=ax2+bx+c,由题意得:
,
解得,
∴二次函数的表达式为y=x2+2x﹣1;
(2)由(1)知,直线AB的表达式为y=﹣x﹣1,二次函数的对称轴为直线x=﹣1.
设直线y=﹣x﹣1与二次函数图象的对称轴交于点D,则点D(﹣1,0),
把x=﹣1代入y=x2+2x﹣1得:y=﹣2,
∴点C(﹣1,﹣2),
∴△ABC的面积=;
(3)在该二次函数的对称轴上存在点Q,使得△ABQ是以AB为腰的等腰三角形;理由如下:
设点Q(﹣1,m),
∵点B(0,﹣1),A(﹣3,2),
∴AB2=18,AQ2=4+(2﹣m)2,BQ2=1+(m+1)2.
分两种情况:
①当AB=AQ时,18=4+(2﹣m)2,
解得,
∴点Q的坐标为或;
②当AB=BQ时,18=1+(m+1)2,
解得,
∴点Q的坐标为或.
综上所述,在该二次函数的对称轴上存在点Q,使得△ABQ是以AB为腰的等腰三角形;点Q的坐标为或或或.
【点评】本题是二次函数综合题,考查了待定系数法,等腰三角形的性质,两点距离公式等知识,利用分类讨论思想解决问题是解题的关键.
15.【解答】解:(1)当y=0时,x2﹣3x﹣4=0,
解得x=4或x=﹣1,
∴A(﹣1,0),B(4,0),
当x=0时,y=﹣4,
∴C(0,﹣4),
设直线BC的解析式为y=kx﹣4,
将点B代入可得4k﹣4=0,
解得k=1,
∴直线BC的解析式为y=x﹣4;
(2)∵点P的横坐标为m,
∴P(m,m﹣4),则E(m,m2﹣3m﹣4),F(m,0),
∴PF=4﹣m,PE=﹣m2+4m,
∵PF=2PE,
∴4﹣m=2(﹣m2+4m),
解得m=4(舍)或m=;
(3)存在m使得△CPE为等腰直角三角形,理由如下:
由(2)可得,PC2=2m2,PE2=(m2﹣4m)2,CE2=m2+(m2﹣3m)2,
当∠PCE=90°时,PE2=2PC2,即(m2﹣4m)2=4m2,
解得m=2或m=6(舍);
当∠CEP=90°时,2CE2=PC2,即2m2+2(m2﹣3m)2=2m2,
解得m=3或m=0(舍);
综上所述:m的值为3或2.
【点评】本题考查二次函数的图象及性质,熟练掌握二次函数的图象及性质,等腰直角三角形的性质是解题的关键.
16.【解答】解:(1)由二次函数y=ax2+bx+c的图象交x轴于A(﹣2,0),B(1,0),设二次函数的解析式为:y=a(x+2)(x﹣1),
把C(0,2)代入得:2=a(0+2)(0﹣1),
解得a=﹣1,
∴二次函数的解析式为y=﹣(x+2)(x﹣1)=﹣x2﹣x+2,
答:二次函数的解析式为y=﹣x2﹣x+2;
(2)在直线AC上方的抛物线上存在点N,使△NAC的面积最大,
过N作ND∥y轴,交AC于D,如图:
设直线AC的解析式为y=kx+b,把A(﹣2,0)、C(0,2)代入得:
,
解得:,
∴直线AC的解析式为y=x+2,
设N(n,﹣n2﹣n+2),则D(n,n+2),
∴ND=(﹣n2﹣n+2)﹣(n+2)=﹣n2﹣2n,
∴S△NAC=ND |xC﹣xA|=×(﹣n2﹣2n)×2=﹣n2﹣2n=﹣(n+1)2+1,
∵﹣1<0,
∴当n=﹣1时,S△NAC有最大值为1,此时N(﹣1,2),
答:在直线AC上方的抛物线上存在点N(﹣1,2),使△NAC的面积最大为1;
(3)在x轴上存在点M,使以B、C、M为顶点的三角形是等腰三角形,
设M(t,0),而B(1,0),C(0,2),
∴BM2=(t﹣1)2,CM2=t2+4,BC2=12+22=5,
①当BC=CM时,t2+4=5,
解得t=1(与B重合,舍去)或t=﹣1,
∴M(﹣1,0);
②当BM=BC时,(t﹣1)2=5,
解得t=+1或t=﹣+1,
∴M(+1,0)或(﹣+1,0);
③当BM=CM时,(t﹣1)2=t2+4,
解得t=﹣,
∴M(﹣,0),
综上所述,M坐标为(﹣1,0)或(+1,0)或(﹣+1,0)或(﹣,0).
【点评】本题考查函数综合应用,涉及待定系数法、三角形面积、等腰三角形判定等知识,解题的关键是用含字母的代数式表示相关点坐标及相关线段的长度.
1.如图,已知抛物线y=﹣x2+bx+c经过B(﹣3,0),C(0,3)两点,与x轴的另一个交点为A.
(1)求抛物线的解析式;
(2)在抛物线对称轴上找一点E,使得AE+CE的值最小,直接写出点E的坐标;
(3)设点P为x轴上的一个动点,是否存在使△BPC为等腰三角形的点P,若存在,直接写出点P的坐标;若不存在,说明理由.
2.如图,已知抛物线y=ax2+bx﹣2(a≠0)经过点A(﹣3,2),与y轴交于点B,其对称轴为直线,为y轴上一点,直线AC与抛物线交于另一点D.
(1)求抛物线的函数表达式;
(2)试在线段AD下方的抛物线上求一点E,使得△ADE的面积最大,并求出最大面积;
(3)在抛物线的对称轴上是否存在一点F,x轴上一点N,使得△DNF是等腰直角三角形?如果存在,求点F的坐标;如果不存在,请说明理由.
3.如图,抛物线y=﹣x2+bx+c经过点A(3,0)与点C(0,3).
(1)求抛物线对应的函数解析式,并写出抛物线与x轴的交点B的坐标;
(2)点P在线段AC上,过点P作x轴的垂线与抛物线交于点Q,直线PQ交x轴于点M,连接CQ,OP,如果S△CPQ=2S△OPM,求PM的长;
(3)探究抛物线的对称轴上是否存在一点E,使得以点E,B,C为顶点的三角形是等腰三角形?若存在,请求出所有符合条件的点的坐标,若不存在,请说明理由.
4.如图,在平面直角坐标系中,点O为坐标原点,抛物线与x轴交于点A、点B(点A在点B的左侧),与y轴交于点C,直线y=4ax﹣12a经过点B、点C.
(1)求抛物线的解析式;
(2)如图1,点P在第二象限的抛物线上,PE∥AB交线段BC于点E,设点P的横坐标为t,PE的长为d,求d与t的函数关系式;(直接写出t的取值范围)
(3)在(2)的条件下,连接OP,点Q在线段OB上,过点Q作QF∥OP交PE于点F,过点Q作QD⊥OB,QD交BC于点D,连接CF、FD,当△FCD为CF为腰的等腰直角三角形时,求点D的坐标.
5.如图,关于x的二次函数y=x2+bx+c的图象与x轴相交于点A(1,0)和点B(3,0),与y轴相交于点C.
(1)求二次函数的表达式和线段BC的长;
(2)在抛物线对称轴上找一点P,使△PBC为等腰三角形?直接写出点P的坐标.
6.如图,抛物线y=x2+bx+c与x轴交于A(﹣2,0),B(4,0)两点,与y轴交于点C,连接AC、BC,点P是第四象限内抛物线上的一个动点,点P的横坐标为m,过点P作PM⊥x轴,垂足为点M,PM交BC于点Q.
(1)求抛物线的解析式;
(2)运动过程中是否存在点P,使线段PQ的值最大?若存在,请求出这个最大值并求出此时P点的坐标;若不存在,请说明理由;
(3)试探究在点P的过程中,是否存在这样的点Q,使得以A、C、Q为顶点的三角形是等腰三角形?若存在,请求出此时点Q的坐标;若不存在,请说明.
7.如图,已知抛物线y=ax2+bx﹣3的图象与x轴交于点A(1,0)和B(3,0),与y轴交于点C,点D是抛物线的顶点,对称轴与x轴交于点E.
(1)求抛物线的解析式;
(2)如图1,在抛物线的对称轴DE上求作一点M,使△AMC的周长最小,并求出点M的坐标和周长的最小值;
(3)如图2,点P是x轴上动点,过点P作x轴的垂线分别交抛物线和直线BC于点F、G.设点P的横坐标为m,是否存在点P,使△FCG是以FG为腰的等腰三角形?若存在,直接写出m的值;若不存在,请说明理由.
8.如图,抛物线y=ax2+3x+c(a≠0)与x轴交于点A(﹣2,0)和点B,与y轴交于点C(0,8),点P为直线BC上方抛物线上的动点,连接CP,PB,直线BC与抛物线的对称轴l交于点E.
(1)求抛物线的解析式;
(2)求△BCP的面积最大值;
(3)点M是抛物线的对称轴l上一动点.是否存在点M,使得△BEM为等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
9.如图,抛物线y=ax2+bx+c的对称轴为x=﹣1,该抛物线与x轴交于A、B两点,且A点坐标为(1,0),交y轴于C(0,3),设抛物线的顶点为D.
(1)求该抛物线的解析式与顶点D的坐标;
(2)在对称轴上是否存在一点P,使得△ACP为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
10.如图,抛物线的顶点D坐标是(1,﹣4),与x轴交于点A(﹣1,0),点B,与y轴交于点C.
(1)求抛物线的表达式;
(2)将抛物线沿着射线CB方向平移个单位长度,平移后新抛物线的顶点是点E,求△ABE的面积.
(3)点P是抛物线对称轴上的一点,点M是对称轴左侧抛物线上的一点,是否存在以PB为腰的等腰直角△PMB,如果存在,直接写出点M的坐标;如果不存在,请说明理由.
11.如图,在平面直角坐标系中,抛物线y=ax2﹣3x+c与x轴交于点A(﹣4,0)和点C,与y轴交于点B(0,4),点P是抛物线上一动点.
(1)求抛物线的解析式;
(2)动点P在抛物线上,且在直线AB上方,求△ABP面积的最大值及此时点P的坐标;
(3)在(2)的条件下,点F为抛物线顶点,Q为抛物线的对称轴上任意一点,若△PFQ是等腰三角形,求出所有符合条件的点Q的坐标.
12.如图,抛物线y=ax2+bx+c的对称轴为直线,且经过A(﹣4,0),C(0,2)两点,与x轴交于另一点B.
(1)求抛物线的解析式;
(2)若点P为直线AC上方的抛物线上的一点,连接PA,PC,求△PAC的面积的最大值,并求出此时点P的坐标;
(3)在对称轴上是否存在点Q,使△QBC为等腰三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
13.如图,二次函数y=﹣x2+(k﹣1)x+4的图象与y轴交于点A与x轴的负半轴交于点B,且△AOB的面积为6.
(1)求A,B两点的坐标;
(2)求该二次函数的表达式;
(3)如果点p在坐标轴上,且△ABP是等腰三角形,直接写出p点坐标.
14.如图,二次函数的图象的顶点C的横坐标为﹣1,直线y=﹣x+n与该二次函数的图象交于A,B两点,其中点A的坐标为(﹣3,2),点B在y轴上.
(1)求n的值及二次函数的表达式.
(2)求△ABC的面积.
(3)在该二次函数的对称轴上是否存在点Q,使得△ABQ是以AB为腰的等腰三角形?若存在,请求出符合条件的Q点的坐标;若不存在,请说明理由.
15.综合与探究
如图,抛物线y=x2﹣3x﹣4与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,连接BC.若点P在线段BC上运动(点P不与点B,C重合),过点P作x轴的垂线,交抛物线于点E,交x轴于点F.设点P的横坐标为m.
(1)求点A,B,C的坐标,并直接写出直线BC的函数解析式.
(2)若PF=2PE,求m的值.
(3)在点P的运动过程中,是否存在m使得△CPE为等腰直角三角形?若存在,请直接写出m的值;若不存在,请说明理由.
16.如图,二次函数y=ax2+bx+c的图象交x轴于A(﹣2,0),B(1,0),交y轴于C(0,2).
(1)求二次函数的解析式;
(2)连接AC,在直线AC上方的抛物线上是否存在点N,使△NAC的面积最大,若存在,求出这个最大值及此时点N的坐标,若不存在,说明理由;
(3)若点M在x轴上,是否存在点M,使以B、C、M为顶点的三角形是等腰三角形,若存在,直接写出点M的坐标;若不存在,说明理由.
参考答案
1.【解答】解:(1)已知抛物线y=﹣x2+bx+c经过B(﹣3,0),C(0,3)两点,将点B,点C的坐标代入得:
,
解得,
故抛物线的解析式为y=﹣x2﹣2x+3;
(2)∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴抛物线的对称轴为直线x=﹣1,
∵点A、B关于直线l对称,
∴BC与对称轴l的交点即为点E,如图,
则此时AE+CE=BE+CE=BC为最小,
设直线BC的解析式为y=mx+n,将点B,点C的坐标代入得:
,
解得,
∴直线BC的解析式为y=x+3;
当x=﹣1时,y=x+3=2,
∴点E(﹣1,2);
(3)∵B(﹣3,0),C(0,3),
∴OB=OC=3,
∴,
当B为顶角的顶点时,
则,
∴点P的坐标为或;
当C为顶角的顶点时,
则PC=BC,
∴点P与点B关于y轴对称,
∴点P的坐标为(3,0);
当BC为底边时,
则PC=PB,即点P在线段BC的垂直平分线上,
∴点P的坐标为(0,0);
综上,点P的坐标为(0,0)或(3,0)或或.
【点评】主要属于二次函数综合题,主要考查了二次函数的图象与性质,等定系数法求函数解析式,解答本题的关键是利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度.
2.【解答】解:(1)由题意得:,
解得:
∴y=x2﹣x﹣2;
(2)由点A、C的坐标得,直线AC的表达式为:y=﹣x+,
联立上式和抛物线的表达式得:﹣x+=x2﹣x﹣2,
解得:x=﹣3(舍去)或5,
∴D(5,﹣2),
过点E作EG∥y轴交AC于点G,
设E(x,x2﹣x﹣2),则G(x,﹣x+),
∴EG=﹣x+﹣x2+x+2,
∴S△ADE=×8(﹣x+﹣x2+x+2)=﹣(x﹣1)2+,
∵﹣3<x<5,
∴当x=1时,△ADE的面积最大为,
此时E(1,﹣);
(3)存在一点F,x轴上一点N使得△DNF是等腰直角三角形,理由如下:
∵抛物线对称轴为直线x=,
设N(x,0),
如图1:当∠FND=90°,NF=DN时,过点N作HI⊥x轴,过点F作FH⊥HI交于H点,过点D作DI⊥HI交于点I,
∵∠FND=90°,
∴∠FNH+∠DNI=90°,
∵∠FNH+∠HFN=90°,
∴∠DNI=∠HFN,
∴△FHN≌△NID(AAS),
∴FH=NI=2,HN=ID,
∴|x﹣|=2,
解得x=或x=,
则DI=5﹣=或DI=5﹣=,
则F(,)或(,);
如图2,当∠FDN=90°,DF=DN时,过点K作KL∥x轴交对称轴于点K,过点N作NL⊥KL交于L点,
同理可证△FKD≌△DLN(AAS),
∴NL=KD=2,DL=FK,
∵KD=5﹣=≠2,
∴此情况不存在;
如图3,当∠NFK=90°,NF=FD,过F点作TS∥x轴,过点N作TN⊥TS交于点T,过点D作DS⊥TS交于点S,
同理可证△FNT≌△DFS(AAS),
∴NT=SF,DS=TF,
∴NT=,
∴F(,﹣);
综上所述:F点坐标为(,)或(,)或(,﹣).
【点评】本题考查二次函数的图象及性质,熟练掌握二次函数的图象及性质,等腰直角三角形的性质,三角形全等的判定及性质,勾股定理是解题的关键.
3.【解答】解:(1)将A(3,0),点C(0,3)代入抛物线y=﹣x2+bx+c得:
,
解得,
∴抛物线对应的函数解析式为y=﹣x2+2x+3,
令y=0,则﹣x2+2x+3=0,
解得x1=﹣1,x2=3,
∴抛物线与x轴的交点B的坐标为(﹣1,0);
(2)设点P的横坐标为m,则Q(m,﹣m2+2m+3),M(m,0),
设直线AC的解析式为y=kx+n,
将A(3,0),C(0,3)代入得,
解得,
∴直线AC的解析式为y=﹣x+3,
∴P(m,﹣m+3),
∴PQ=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m,PM=﹣m+3,
∵S△CPQ=2S△OPM,
∴PQ OM=2×OM PM,
∴PQ=2PM,
即﹣m2+3m=2(﹣m+3),
解得m=2或3(舍去),
∴PM=﹣m+3=1;
(3)如图:
∵y=﹣x2+2x+3,
∴抛物线的对称轴为x=﹣=1,
设点E的坐标为(1,a),
∵B(﹣1,0),C(0,3),
∴BC2=12+32=10,
BE2=22+a2=4+a2,
CE2=12+(a﹣3)2=a2﹣6a+10,
当BC=BE时,4+a2=10,
解得a=±,
∴点E的坐标为(1,)或(1,﹣);
当BC=CE时,a2﹣6a+10=10,
解得a=0或6(此时,点B、C、E在同一直线上,舍去),
∴点E的坐标为(1,0);
当CE=BE时,4+a2=a2﹣6a+10,
解得a=1,
∴点E的坐标为(1,1);
综上,存在,点E的坐标为(1,)或(1,﹣)或(1,0)或(1,1).
【点评】本题是二次函数综合题,考查了抛物线与x轴的交点,二次函数图象和性质,待定系数法求函数解析式,用点的坐标表示线段长度,等腰三角形的性质等知识,关键是对二次函数性质的掌握和运用以及分类思想的运用.
4.【解答】解:(1)在直线y=4ax﹣12a中,
当y=0时,4ax﹣12a=0,
∴x=3,
∴B的坐标为(3,0),
把点B的坐标(3,0)代入抛物线中得:﹣×9+3a﹣12a=0,
∴a=﹣,
∴抛物线的解析式为:y=﹣x2﹣x+6;
(2)由(1)得:C(0,6),
当y=0时,﹣x2﹣x+6=0,
解得:x1=3,x2=﹣4,
∴A的坐标为(﹣4,0),
设BC的解析式为:y=kx+n,
∴,
解得:,
∴BC的解析式为:y=﹣2x+6,
设点E的坐标为(x,﹣2x+6),
∵点P的横坐标为t,
∴P(t,﹣t2﹣t+6),
∵PE∥x轴,
∴﹣2x+6=﹣t2﹣t+6,
∴x=t2+t,
∴d=t2+t﹣t=t2﹣t(﹣4<t<0);
(3)如图3,延长QD,PE交于点G,
设点D的坐标为(m,﹣2m+6),则Q(m,0),
∵OP∥FQ,PE∥AB,
∴四边形POQF是平行四边形,
∴PF=OQ=m,
∵DQ⊥x轴,PE∥x轴,
∴∠G=90°,
∵△CFD是以CF为腰的等腰直角三角形,
∴CF=DF,∠CFD=90°,
∴∠CFH+∠DFG=90°,
∵∠CHF=∠CFH+∠FCH=90°,
∴∠DFG=∠FCH,
∴△CFH≌△FDG(AAS),
∴FH=DG,CH=FG,
∴,
解①得:t2+3t=0,
∴t1=0(舍),t2=﹣3,
把t=﹣3代入②中得:3﹣m=﹣++6﹣(﹣2m+6),
∴m=2,
∴D(2,2).
【点评】本题为二次函数的综合题,涉及待定系数法,函数与方程,三角形全等的性质和判定,等腰直角三角形的性质,平行四边形的性质和判定,坐标与图形的性质等知识点.在(1)中求出B的坐标是解题的关键,在(2)中求得直线BC解析式是解题的关键,在(3)证明△CFH≌△FDG是解题的关键.本题考查知识点较多,计算量较大,综合性较强.
5.【解答】解:(1)把A(1,0)和C(0,3)代入y=x2+bx+c,,
解得:,
∴二次函数的表达式为:y=x2﹣4x+3;
令抛物线y=0,则x2﹣4x+3=0,
解得x=1或x=3,
根据题意:B(3,0),
∵C(0,3),
则BC=3;
(2)存在.
理由:∵BC=3,
设点P(2,m),
由点P、B、C的坐标得,PB2=1+m2,BC=18,PC2=4+(m﹣3)2,
当PB=BC时,
则1+m2=18,则m=±,即点P(2,1±)
当PB=PC或BC=PC时,
同理可得:18=4+(m﹣3)2或1+m2=4+(m﹣3)2,
解得:m=2或3±,
即点P(2,2)或(2,3±),
综上,P(2,1±)或(2,2)或(2,3±).
【点评】本题是二次函数的综合题型,其中涉及到运用待定系数法求二次函数,等腰三角形的性质,轴对称的性质等知识,运用数形结合、分类讨论思想是解题的关键.
6.【解答】解:(1)把A(﹣2,0),B(4,0)代入y=x2+bx+c得,,
解得,
∴抛物线的解析式为y=x2﹣2x﹣8;
(2)存在,
∵抛物线y=x2+bx+c与y轴交于点C,
∴C(0,﹣8),
设直线BC的解析式为y=kx+n,
∴,
解得,
∴直线BC的解析式为y=2x﹣8,
∵点P的横坐标为m,过点P作PM⊥x轴,
∴P(m,m2﹣2m﹣8),Q(m,2m﹣8),
∴PQ=2m﹣8﹣(m2﹣2m﹣8)=﹣m2+4m=﹣(m﹣2)2+4,
∴当m=2时,线段PQ的值最大,这个最大值为4,
此时P点的坐标为(2,﹣8);
(3)由(2)直线BC的解析式为y=2x﹣8,
设Q(m,2m﹣8)(0<m<4),
当CQ=CA时,m2+(2m﹣8+8)2=68,
解得m1=,m2=﹣(舍去);
∴Q(,﹣8),
当AQ=AC时,(m+2)2+(2m﹣8)2=68,
解得:m1=(舍去),m2=0(舍去);
当QA=QC时,(m+2)2+(2m﹣8)2=m2+(2m)2,
解得m=,
∴Q(,﹣).
综上所述,满足条件的Q点坐标为(,﹣8)或(,﹣).
【点评】本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和等腰三角形的性质;会利用待定系数法求函数解析式;理解坐标与图形性质,会利用勾股定理表示线段之间的关系;会运用分类讨论的思想解决数学问题.
7.【解答】解:(1)已知抛物线y=ax2+bx﹣3的图象与x轴交于点A(1,0)和B(3,0),将点A、B的坐标代入得:
,
解得,
∴抛物线的解析式为y=﹣x2+4x﹣3;
(2)如图,连接BC交DE于点M,此时MA+MC最小,
又∵AC是定值,所以此时△AMC的周长最小.
令x=0时,则有y=﹣3,即C(0,﹣3),
∴OB=OC=3,OA=1,
∴;
同理,
∴此时△AMC的周长=;
∵DE是抛物线的对称轴,抛物线与x轴交点A(1,0)和B(3,0),
∴AE=BE=1,对称轴为x=2,
由OB=OC,∠BOC=90°得∠OBC=45°,
∴EB=EM=1,
又∵点M在第四象限,且在抛物线的对称轴上,
∴M(2,﹣1);
(3)存在点P,使△FCG是以FG为腰的等腰三角形;m=4或或;理由如下:
设直线BC的解析式为y=kx+b,把点B、C坐标代入得:
,
解得:,
∴直线BC的解析式为y=x﹣3,
∵点P的横坐标为m,
∴点F(m,﹣m2+4m﹣3),点G(m,m﹣3),
则FG2=(m﹣m)2+(﹣m2+4m﹣3﹣m+3)2=(﹣m2+3m)2,CF2=(m2﹣4m)2+m2,GC2=(m﹣0)2+(m﹣3+3)2=2m2,
当FG=FC时,则(﹣m2+3m)2=(m2﹣4m)2+m2,
解得m=0(舍去)或4;
当FG=CG时,则(﹣m2+3m)2=2m2,
解得m=0(舍去)或;
综上,存在点P,使△FCG是以FG为腰的等腰三角形;m=4或或.
【点评】本题考查的是二次函数综合运用,涉及到一次函数的性质、点的对称性、等腰三角形的性质等,其中(3),要注意分类求解,避免遗漏.
8.【解答】解:(1)将A(﹣2,0),C(0,8)代入y=ax2+3x+c,得:
,
解得,
∴;
(2)令y=0,则,
解得x=﹣2或x=8,
∴B(8,0),
设直线BC的解析式为y=kx+b,代入得:
,
解得,
∴y=﹣x+8,
过点P作PG∥y轴交BC于G,
设,则G(t,﹣t+8),
∴,
∴,
∴当t=4时,△BCP的面积有最大值,最大值为32;
(3)存在点M,使得△BEM为等腰三角形,理由如下:
∵,
∴抛物线的对称轴为直线x=3,
∴E(3,5),设M(3,m),
∴,,EM=|m﹣5|,
当BE=BM时,,
解得m=5(舍)或m=﹣5,
∴M(3,﹣5);
当BE=EM时,,
解得或,
∴或;
当BM=EM时,,
解得m=0,
∴M(3,0);
综上所述:M点坐标为(3,0)或(3,﹣5)或或.
【点评】本题考查了二次函数综合,待定系数法求二次函数解析式,二次函数综合﹣面积问题以及特殊三角形问题,熟练掌握二次函数的性质是解本题的关键.
9.【解答】解:(1)点A(1,0)关于x=﹣1的对称点B(﹣3,0),
设过A(1,0)、B(﹣3,0)的抛物线为y=a(x﹣1)(x+3),
该抛物线又过C(0,3),则有:3=﹣3a,解得a=﹣1,
即y=﹣(x+1)2+4=﹣x2﹣2x+3,顶点D为(﹣1,4);
(2)在对称轴上存在一点P,使得△ACP为等腰三角形;点P的坐标为(﹣1,1)或(﹣1,)或(﹣1,)或(﹣1,0).理由如下:
设P(﹣1,t),
∵A(1,0),C(0,3),
∴AP2=(1+1)2+t2=4+t2,CP2=12+(t﹣3)2=t2﹣6t+10,AC2=12+32=10,
∵△APC为等腰三角形,
∴有AP=CP、AP=AC和CP=AC三种情况,
①当AP=CP时,则有AP2=CP2,即4+t2=t2﹣6t+10,
解得t=1,
此时P(﹣1,1);
②当AP=AC时,则有AP2=AC2,即4+t2=10,
解得t=,
此时P(﹣1,)或(﹣1,);
③当CP=AC时,则有CP2=AC2,即t2﹣6t+10=10,
解得t=0或t=6,
此时P(﹣1,0)或P(﹣1,6),
设直线AC解析式为y=kx+b,将点A,点C的坐标代入得:
,
解得:,
∴直线AC解析式为y=﹣3x+3,
当x=﹣1时y=6,则P(﹣1,6)在直线AC上,
综上,在对称轴上存在一点P,使得△ACP为等腰三角形;点P的坐标为(﹣1,1)或(﹣1,)或(﹣1,)或(﹣1,0).
【点评】本题属于二次函数综合题,主要考查了二次函数的综合应用,待定系数法求解析式,等腰三角形的性质,勾股定理,解答本题的关键是熟练掌握二次函数的图象与性质.
10.【解答】解:(1)∵抛物线的顶点D的坐标为(1,﹣4),
∴设抛物线的函数关系式为y=a(x﹣1)2﹣4,
把点A(﹣1,0)代入得:0=a(﹣1﹣1)2﹣4,
解得:a=1,
∴抛物线的函数关系式为y=(x﹣1)2﹣4,即y=x2﹣2x﹣3;
(2)当x=0时,y=3,
∴C(0,﹣3),
∵顶点D坐标是(1,﹣4),
∴对称轴是:直线x=1,
∵抛物线与x轴交于点A(﹣1,0),
∴B(3,0),
∴OB=OC=3,
∵∠BOC=90°,
∴△BOC是等腰直角三角形,
∵将抛物线沿着射线CB方向平移个单位长度,
∴将抛物线向上平移3个单位,再向右平移3个单位,得到的解析式为:y=(x﹣1﹣3)2﹣4+3,即y=(x﹣4)2﹣1,
∴平移后新抛物线的顶点是点E的坐标为(4,﹣1),如图1,
∴△ABE的面积=×4×1=2;
(3)点P是抛物线对称轴上的一点,点M是对称轴左侧抛物线上的一点,当△PMB是以PB为腰的等腰直角三角形时,分以下几种情况讨论:
①当∠BPM=90°时,PM=PB,如图2,
∴M点与A点重合,
∴M(﹣1,0);
②当∠PBM=90°时,PB=BM,
如图3,当P点在M点上方时,过点B作x轴的垂线GH,过点P作PH⊥GB于点H,过点M作MG⊥HG于点G,
∵∠PBM=90°,
∴∠PBH+∠MBG=90°,
∵∠H=∠PBH+∠BPH=90°,
∴∠MBG=∠BPH,
∵BP=BM,∠H=∠G=90°,
∴△BPH≌△MBG(AAS),
∴BH=MG,PH=BG=2,
设P(1,t),则M(3﹣t,﹣2),
∴﹣2=(3﹣t)2﹣2(3﹣t)﹣3,
解得:t1=2+,t2=2﹣,
∴点M的坐标为(1﹣,﹣2)或(1+,﹣2),
∵M点在对称轴的左侧,
∴M点的坐标为(1﹣,﹣2);
③如图4,当P点在M点下方时,PB=PM,过点B作TS⊥x轴,过点M作MT⊥TS于T,过点P作PS⊥TS于S,
∵∠PBM=90°,
∴∠PBS+∠MBT=90°,
∵∠PBS+∠BPS=90°,
∴∠MBT=∠BPS,
∵BP=BM,∠T=∠S=90°,
∴△BPS≌△MBT(AAS),
∴BS=MT,PS=BT=2,
设P(1,t),则M(3+t,2),
∴2=(3+t)2﹣2(3+t)﹣3,
解得:t1=﹣2+,t2=﹣2﹣,
∴点M的坐标为(1﹣,2)或(1+,2),
∵M点在对称轴的左侧,
∴M点的坐标为(1﹣,﹣2);
综上所述,点M的坐标为(﹣1,0)或(1﹣,﹣2)或(1﹣,﹣2).
【点评】本题考查了二次函数的综合问题,待定系数法求二次函数关系式,全等三角形的性质和判定,等腰直角三角形的性质和判定,平移的原则等知识,正确作辅助线构建全等三角形,并注意用分类讨论的思想解决问题.
11.【解答】解:(1)抛物线y=ax2﹣3x+c与x轴交于点A(﹣4,0)和点C,与y轴交于点B(0,4),将点A,点B的坐标代入得:
,
解得:,
∴抛物线的解析式为y=﹣x2﹣3x+4;
(2)设直线AB的解析式为y=kx+b,将点A,点B的坐标代入得:
,
解得:,
∴直线AB的解析式为y=x+4,
过点P作x轴的垂线交AB于点H,如图:
设P(x,﹣x2﹣3x+4),
∴H(x,x+4),
∴PH=﹣x2﹣3x+4﹣(x+4)=﹣x2﹣4x,
∵△ABP面积=×PH×AO,
∴S△ABP=×(﹣x2﹣4x)×4=﹣2x2﹣8x=﹣2(x+2)2+8,
∴当x=﹣2时,△ABP面积最大值为8,
此时P(﹣2,6);
(3)抛物线整理得:y=﹣x2﹣3x+4=,
∴顶点F的坐标为,对称轴为直线,
设点Q的坐标为,
∴QF2=,PF2==,PQ2=,
当QF=PF时,则=,
解得:,,
∴此时点Q的坐标为:,;
当QF=PQ时,则=,
解得:,
∴点Q的坐标为:;
当PQ=PF时,=,
解得:m1=,m2=,
当m=时,P、Q重合,不合题意,舍去,
∴此时点Q的坐标为(﹣,);
综上所述,点Q的坐标为(,),(﹣,),(﹣,),(,).
【点评】本题属于二次函数综合题,主要考查二次函数的图象与性质,一次函数的图象与性质,待定系数法求函数解析式,等腰三角形的定义,熟练掌握二次函数的性质是解题的关键.
12.【解答】解:(1)抛物线y=ax2+bx+c的对称轴为直线,且经过A(﹣4,0),C(0,2)两点,与x轴交于另一点B.
由抛物线的对称性可知:点A与点B关于直线对称,
∴点B的坐标为(1,0),
设抛物线解析式为y=a(x+4)(x﹣1),把点C的坐标代入得:
2=﹣4a,
解得:,
∴;
(2)点P为直线AC上方的抛物线上的一点,设,
如图,过点P作PQ⊥x轴交AC于点Q,
设直线AC的解析式为y=kx+b1,将A(﹣4,0),C(0,2)代入得:
,
解得:,
∴直线AC的解析式为y=,
∴Q(m,m+2),
∴PQ=m+2﹣(m+2)=﹣2m,
∴S△PAC=PQ×4=2PQ=﹣m2﹣4m=﹣(m+2)2+4,
∴当m=﹣2时,S△PAC的最大值是4,此时P(﹣2,3).
(3)设点,
∵B(1,0),C(0,2),
当QB=QC时,,
解得:q=0,即;
当QB=BC时,,该方程无解;
当QC=BC时,,
解得:,即或.
综上,当点Q的坐标为或或.
【点评】本题属于二次函数综合题,主要考查了求二次函数解析式、二次函数与面积综合、二次函数与几何综合等知识点,掌握分类讨论思想成为解题的关键.
13.【解答】解:(1)∵二次函数y=﹣x2+(k﹣1)x+4的图象与y轴交于点A,
∴令x=0,得y=4,即A(0,4),OA=4.
∵△AOB的面积为6,
∴,
∵OA=4,
∴OB=3,
∴B(﹣3,0);
(2)∵二次函数y=﹣x2+(k﹣1)x+4的图象与x轴的负半轴交于点B,
又∵B(﹣3,0),
∴﹣(﹣3)2+(﹣3)(k﹣1)+4=0,
解得,
故二次函数解析式为;
(3)∵A(0,4),B(﹣3,0),
∴OA=4,OB=3,
∵∠BOA=90°,
∴.
①如图1,当AB=AP,P在x轴上时,
∵AB=AP,AO⊥BP,
∴OB=OP=3,
∴P(3,0);
②如图2,当AB=AP,P在y轴负半轴上时,
∵AB=5,AB=AP,
∴AP=5.
∵OA=4,
∴OP=AP﹣OA=1,
∴P(0,﹣1).
③同理,当AB=AP,P在y轴正半轴上时,
∵AB=5,AB=AP,
∴AP=5.
∵OA=4,
∴OP=AP+OA=9,
∴P(0,9);
④如图3,当BA=BP,P在x轴负半轴上时,
∵AB=5,AB=BP,
∴BP=5.
∵OB=3,
∴OP=OB+BP=3+5=8,
∴P(﹣8,0).
⑤如图4,当BA=BP,P在y轴负半轴上时,
∵AB=BP,BO⊥AP,
∴OA=OP=4,
∴P(0,﹣4).
⑥如图5,当BA=BP,P在x轴正半轴上时,
∵AB=5,AB=BP,
∴BP=5.
∵OB=3,
∴OP=PB﹣OB=5﹣3=2,
∴P(2,0).
⑦如图6,作AB的垂直平分线交y轴于点P1,交x轴于点P2,则有P1A=BP1,P2A=BP2,连接P1B,P2A.
∵A(0,4),B(﹣3,0),
∴OA=4,OB=3
设AP1=x,则P1B=AP1=x,OP1=OA﹣AP1=4﹣x,
在Rt△BOP1中,∠BOP1=90°,
∴,即32+(4﹣x)2=x2,
解得,即,.
∴,
同理,设OP2=y,则AP2=P2B=OP2+OB=y+3,OA=4,
在Rt△AOP2中,∠AOP2=90°,
∴,即42+y2=(y+3)2,
解得,即,
∴,
综上,符合题意的P点坐标为:(3,0),(0,﹣1),(0,9),(﹣8,0),(0,﹣4),(2,0),,.
【点评】本题属于二次函数综合题,主要考查了二次函数的图象与性质,等腰三角形的性质,熟练掌握二次函数相关性质是解题的关键.
14.【解答】解:(1)∵直线y=﹣x+n过点A(﹣3,2),
∴2=3+n,
解得n=﹣1,
∴y=﹣x﹣1.
令x=0,则y=﹣1,
∴点B(0,﹣1).
设二次函数的表达式为y=ax2+bx+c,由题意得:
,
解得,
∴二次函数的表达式为y=x2+2x﹣1;
(2)由(1)知,直线AB的表达式为y=﹣x﹣1,二次函数的对称轴为直线x=﹣1.
设直线y=﹣x﹣1与二次函数图象的对称轴交于点D,则点D(﹣1,0),
把x=﹣1代入y=x2+2x﹣1得:y=﹣2,
∴点C(﹣1,﹣2),
∴△ABC的面积=;
(3)在该二次函数的对称轴上存在点Q,使得△ABQ是以AB为腰的等腰三角形;理由如下:
设点Q(﹣1,m),
∵点B(0,﹣1),A(﹣3,2),
∴AB2=18,AQ2=4+(2﹣m)2,BQ2=1+(m+1)2.
分两种情况:
①当AB=AQ时,18=4+(2﹣m)2,
解得,
∴点Q的坐标为或;
②当AB=BQ时,18=1+(m+1)2,
解得,
∴点Q的坐标为或.
综上所述,在该二次函数的对称轴上存在点Q,使得△ABQ是以AB为腰的等腰三角形;点Q的坐标为或或或.
【点评】本题是二次函数综合题,考查了待定系数法,等腰三角形的性质,两点距离公式等知识,利用分类讨论思想解决问题是解题的关键.
15.【解答】解:(1)当y=0时,x2﹣3x﹣4=0,
解得x=4或x=﹣1,
∴A(﹣1,0),B(4,0),
当x=0时,y=﹣4,
∴C(0,﹣4),
设直线BC的解析式为y=kx﹣4,
将点B代入可得4k﹣4=0,
解得k=1,
∴直线BC的解析式为y=x﹣4;
(2)∵点P的横坐标为m,
∴P(m,m﹣4),则E(m,m2﹣3m﹣4),F(m,0),
∴PF=4﹣m,PE=﹣m2+4m,
∵PF=2PE,
∴4﹣m=2(﹣m2+4m),
解得m=4(舍)或m=;
(3)存在m使得△CPE为等腰直角三角形,理由如下:
由(2)可得,PC2=2m2,PE2=(m2﹣4m)2,CE2=m2+(m2﹣3m)2,
当∠PCE=90°时,PE2=2PC2,即(m2﹣4m)2=4m2,
解得m=2或m=6(舍);
当∠CEP=90°时,2CE2=PC2,即2m2+2(m2﹣3m)2=2m2,
解得m=3或m=0(舍);
综上所述:m的值为3或2.
【点评】本题考查二次函数的图象及性质,熟练掌握二次函数的图象及性质,等腰直角三角形的性质是解题的关键.
16.【解答】解:(1)由二次函数y=ax2+bx+c的图象交x轴于A(﹣2,0),B(1,0),设二次函数的解析式为:y=a(x+2)(x﹣1),
把C(0,2)代入得:2=a(0+2)(0﹣1),
解得a=﹣1,
∴二次函数的解析式为y=﹣(x+2)(x﹣1)=﹣x2﹣x+2,
答:二次函数的解析式为y=﹣x2﹣x+2;
(2)在直线AC上方的抛物线上存在点N,使△NAC的面积最大,
过N作ND∥y轴,交AC于D,如图:
设直线AC的解析式为y=kx+b,把A(﹣2,0)、C(0,2)代入得:
,
解得:,
∴直线AC的解析式为y=x+2,
设N(n,﹣n2﹣n+2),则D(n,n+2),
∴ND=(﹣n2﹣n+2)﹣(n+2)=﹣n2﹣2n,
∴S△NAC=ND |xC﹣xA|=×(﹣n2﹣2n)×2=﹣n2﹣2n=﹣(n+1)2+1,
∵﹣1<0,
∴当n=﹣1时,S△NAC有最大值为1,此时N(﹣1,2),
答:在直线AC上方的抛物线上存在点N(﹣1,2),使△NAC的面积最大为1;
(3)在x轴上存在点M,使以B、C、M为顶点的三角形是等腰三角形,
设M(t,0),而B(1,0),C(0,2),
∴BM2=(t﹣1)2,CM2=t2+4,BC2=12+22=5,
①当BC=CM时,t2+4=5,
解得t=1(与B重合,舍去)或t=﹣1,
∴M(﹣1,0);
②当BM=BC时,(t﹣1)2=5,
解得t=+1或t=﹣+1,
∴M(+1,0)或(﹣+1,0);
③当BM=CM时,(t﹣1)2=t2+4,
解得t=﹣,
∴M(﹣,0),
综上所述,M坐标为(﹣1,0)或(+1,0)或(﹣+1,0)或(﹣,0).
【点评】本题考查函数综合应用,涉及待定系数法、三角形面积、等腰三角形判定等知识,解题的关键是用含字母的代数式表示相关点坐标及相关线段的长度.
同课章节目录
