实数与数轴
图片预览





文档简介
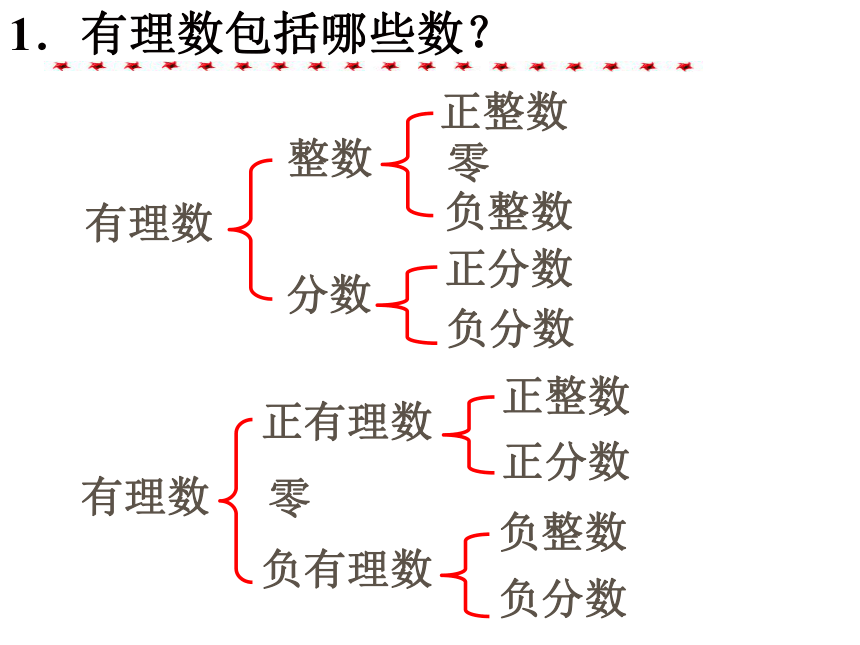
课件14张PPT。12.2实数与数轴(一) 那堪中学 韦广颂1.有理数包括哪些数?有理数整数分数正整数 零负整数正分数负分数有理数正有理数零负有理数正整数正分数负整数负分数2.有理数中的分数能化为小数吗?
化为什么样的小数?举例加以说明
答:任何一个分数写成小数的形式,必是
有限小数或者无限循环小数 例如 实数与数轴(一) 做一做 在数学上已经证明,没有一个有理数的平方
等于2,也就是说, 不是一个有理数. =1.4142135623730950488016887242096980785696
71875376948073176679737990732478462107038
85038753432764157273501384623091229702492
48360558507372126441214970999358314132226
659275055927557999505011527820605715… 无理数:
无限不循环小数叫做无理数
(irrational number).
实数:
有理数与无理数统称为实数
(Real numbers).定 义
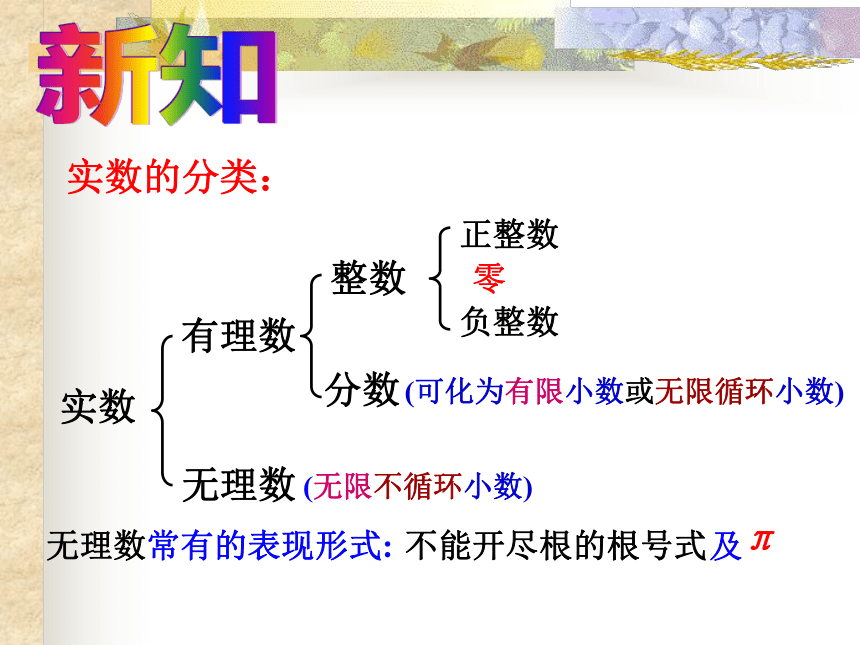
新知实数的分类: 实数 有理数 无理数 整数 分数 正整数 零 负整数 (可化为有限小数或无限循环小数) (无限不循环小数) 无理数常有的表现形式: 不能开尽根的根号式 例1 判断正误,在后面的括号里对的用 “√”,错的记“×”表示,并说明理由.
(1)无理数都是开方开不尽的数.( )
(2)无理数都是无限小数.( )
(3)无限小数都是无理数.( )
(4)无理数包括正无理数、零、负无理数( )
(5)带根号的数都是无理数.( )
(6)有理数都是有限小数.( ) 实数与数轴(一) 实数与数轴(一) 实数的相反数、绝对值意义和有理数是一样的 如: 的相反数是 , 的相反数是 ,
0的相反数是 . 在第2章学过的有关有理数的相反数和绝对值等概念、大小比较、运算法则以及运算律,对于实数也适用.0如图是两个边长1的正方形操作探索拼成的长方形, 其面积是2. 现剪下两个角重新拼成一个 正方形, 新正方形的边长是_____ 下图数轴中, 正方形的对角线长为____, 以原点为圆心, 对角线长为半径画弧截得一点, 该点与原点的距离是____, 该点表示的数是____. 概括 ?
数轴上的任一点表示的数,不是有理数,就是无理数.数学上可以说明:
数轴上的任一点必定表示一个实数;反过来,
每一个实数(有理数或无理数)也都可以用数轴上的点来表示.
换句话说,实数与数轴上的点一一对应. 正实数的大小比较和运算,
通常可取它们的近似值来进行 实数与数轴(一) 实数与数轴(一) 练 习
1.判断下列说法是否正确:
(1)两个数相除,如果不管添多少位小数,永远都除不尽,那么结果一定是一个无理数
(2)任意一个无理数的绝对值是正数.
2.计算: .(结果保留两位小数)
3.比较下列各组数中两个实数的大小:
(1) (2) 小结: 实数与数轴(一) 1.判断一个数是不是无理数,必须看它是否同时满足两个条件:无限小数和不循环小数这两者缺一不可.
2.带根号的数并不都是无理数,而开方开不尽
的数才是无理数.3.掌握实数的不同分类法.
化为什么样的小数?举例加以说明
答:任何一个分数写成小数的形式,必是
有限小数或者无限循环小数 例如 实数与数轴(一) 做一做 在数学上已经证明,没有一个有理数的平方
等于2,也就是说, 不是一个有理数. =1.4142135623730950488016887242096980785696
71875376948073176679737990732478462107038
85038753432764157273501384623091229702492
48360558507372126441214970999358314132226
659275055927557999505011527820605715… 无理数:
无限不循环小数叫做无理数
(irrational number).
实数:
有理数与无理数统称为实数
(Real numbers).定 义
新知实数的分类: 实数 有理数 无理数 整数 分数 正整数 零 负整数 (可化为有限小数或无限循环小数) (无限不循环小数) 无理数常有的表现形式: 不能开尽根的根号式 例1 判断正误,在后面的括号里对的用 “√”,错的记“×”表示,并说明理由.
(1)无理数都是开方开不尽的数.( )
(2)无理数都是无限小数.( )
(3)无限小数都是无理数.( )
(4)无理数包括正无理数、零、负无理数( )
(5)带根号的数都是无理数.( )
(6)有理数都是有限小数.( ) 实数与数轴(一) 实数与数轴(一) 实数的相反数、绝对值意义和有理数是一样的 如: 的相反数是 , 的相反数是 ,
0的相反数是 . 在第2章学过的有关有理数的相反数和绝对值等概念、大小比较、运算法则以及运算律,对于实数也适用.0如图是两个边长1的正方形操作探索拼成的长方形, 其面积是2. 现剪下两个角重新拼成一个 正方形, 新正方形的边长是_____ 下图数轴中, 正方形的对角线长为____, 以原点为圆心, 对角线长为半径画弧截得一点, 该点与原点的距离是____, 该点表示的数是____. 概括 ?
数轴上的任一点表示的数,不是有理数,就是无理数.数学上可以说明:
数轴上的任一点必定表示一个实数;反过来,
每一个实数(有理数或无理数)也都可以用数轴上的点来表示.
换句话说,实数与数轴上的点一一对应. 正实数的大小比较和运算,
通常可取它们的近似值来进行 实数与数轴(一) 实数与数轴(一) 练 习
1.判断下列说法是否正确:
(1)两个数相除,如果不管添多少位小数,永远都除不尽,那么结果一定是一个无理数
(2)任意一个无理数的绝对值是正数.
2.计算: .(结果保留两位小数)
3.比较下列各组数中两个实数的大小:
(1) (2) 小结: 实数与数轴(一) 1.判断一个数是不是无理数,必须看它是否同时满足两个条件:无限小数和不循环小数这两者缺一不可.
2.带根号的数并不都是无理数,而开方开不尽
的数才是无理数.3.掌握实数的不同分类法.
