2024-2025学年人教版九年级数学下册27.1 课时2 相似多边形 课件(共26张PPT)
文档属性
| 名称 | 2024-2025学年人教版九年级数学下册27.1 课时2 相似多边形 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 701.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-05 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
人教版九年级数学下册课件
第二十七章 相似
27.1 图形的相似
课时2 相似多边形
1.理解相似多边形的定义.
2.能根据多边形相似进行相关的计算,会根据条件判断两个多边形是否相似.(重点、难点)
3.在学习相似图形的过程中,提高对相似图形中的对应关系的认识,增强数学推理能力.
学习目标
新课导入
情景导入
怎样从数学的角度刻画“形状相同”呢?这节课就让我们一起来探究相似多边形吧!
相似!
形状相同的两个多边形相似吗?
新课讲解
知识点1 相似多边形与相似比
A1
B1
C1
D1
E1
F1
A
B
C
D
E
F
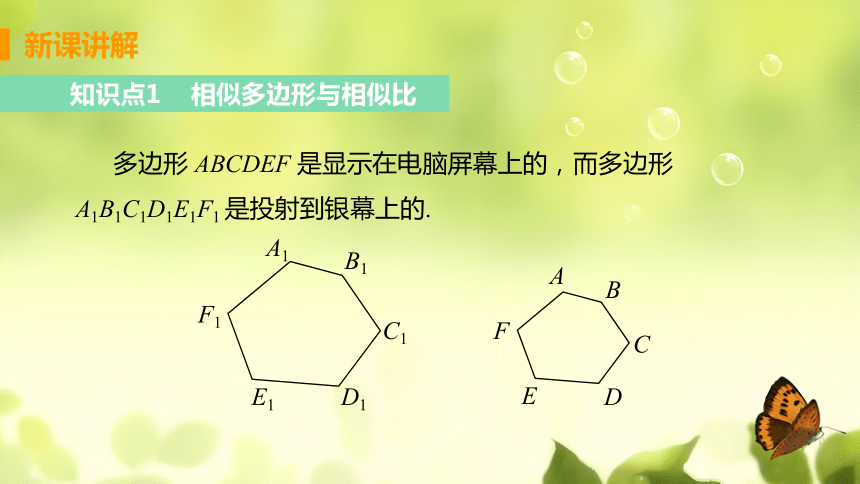
多边形 ABCDEF 是显示在电脑屏幕上的,而多边形 A1B1C1D1E1F1 是投射到银幕上的.
新课讲解
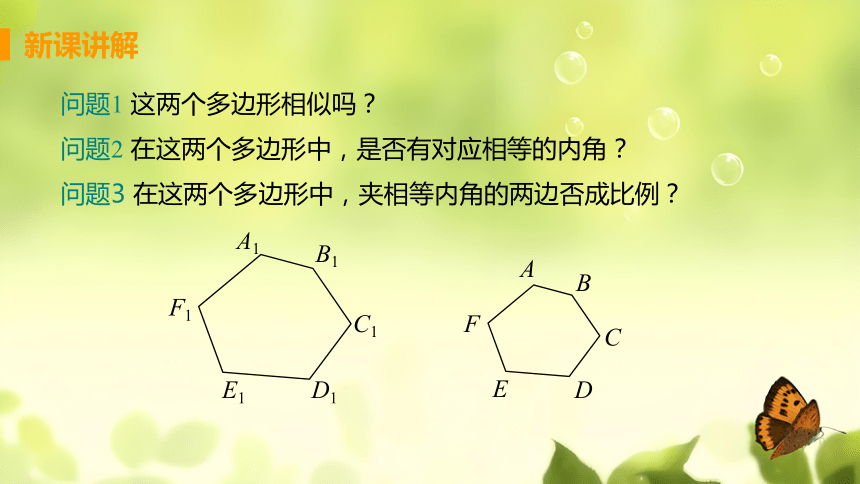
问题1 这两个多边形相似吗?
问题2 在这两个多边形中,是否有对应相等的内角?
问题3 在这两个多边形中,夹相等内角的两边否成比例?
A1
B1
C1
D1
E1
F1
A
B
C
D
E
F
新课讲解
结论
相似多边形的定义:
各角分别相等、各边成比例的两个多边形叫做相似多边形.
相似多边形的特征:
相似多边形的对应角相等,对应边成比例.
相似比:
相似多边形的对应边的比叫作相似比.
新课讲解
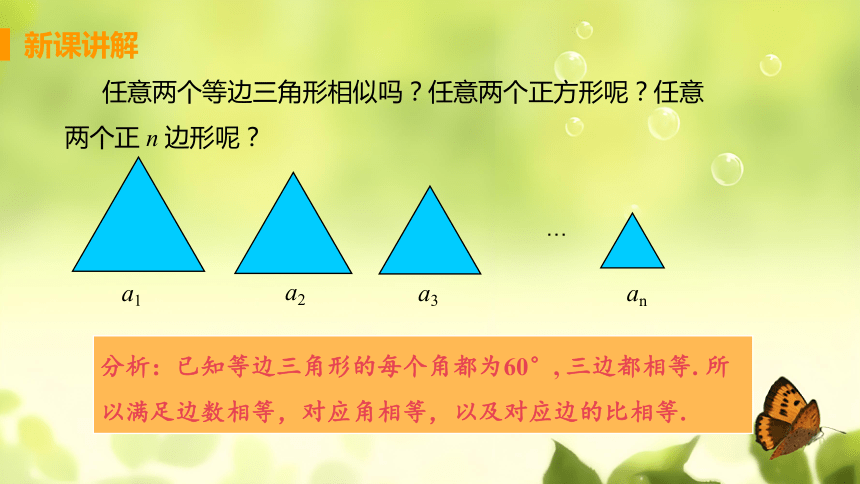
任意两个等边三角形相似吗?任意两个正方形呢?任意两个正 n 边形呢?
a1
a2
a3
an
…
分析:已知等边三角形的每个角都为60°, 三边都相等. 所以满足边数相等,对应角相等,以及对应边的比相等.
新课讲解
同理,任意两个正方形都相似.
归纳:任意两个边数相等的正多边形都相似.
…
a1
a2
a3
an
新课讲解
活学巧记
两个相似多边形,边数相同形状同;
各角对应都相等,各边对应成比例.
(1)相似多边形的定义可用来判定两个多边形是否相似.
(2)相似多边形的性质常用来求相似多边形未知边的长度或未知角的度数.
课堂小结
相似多边形
概念
相似比
性质
对应角相等
对应边成比例
当堂小练
1. 填空:
(1) 如图①是两个相似的四边
形,则x= ,y = ,
α= ;
(2) 如图②是两个相似的矩形,
x= .
╰
65°
╯
80°
α
╭
6
125°
╯
80°
╮
3
x
y
图①
3
5
30
20
15
x
图②
2.5
1.5
90°
22.5
当堂小练
2. 如图所示的两个四边形是否相似?
答案:不相似.
∵四边形ABCD∽四边形A'B'C'D',
∴∠A= ,∠B= ,∠C= ,
∠D= ,= = .
∠D'
∠C'
∠B'
相似多边形的性质
∠A'
(1)对应角 ,对应边的比 .
(2)几何语言(以四边形为例):如图,
相等
相等
知识点
3.(人教9下P27改编)如图,△ABC∽△DEF,∠C=∠F=35°,∠B=115°,则x= ,y= ,∠D= °.
30
3.5
6
(1)如果两个多边形的对应角 ,且 相等,那么这两个多边形相似.
(2)几何语言(以四边形为例):如知识点3的图,
∵ ,
且 ,
∴ .
(3)相似多边形 的比叫做相似比,记作k.
对应边
四边形ABCD∽四边形A'B'C'D'
∠A=∠A',∠B=∠B',∠C=∠C',∠D=∠D'
对应边的比
相似多边形的判定(定义法)
相等
4.两个矩形的边长如图所示.
(1)求证:矩形ABCD∽矩形A'B'C'D';
(2)在(1)中,相似比= .
(1)证明:在矩形ABCD和矩形A'B'C'D'中,
∵∠A=∠A'=90°,∠B=∠B'=90°,
∠C=∠C'=90°,∠D=∠D'=90°,
,
∴矩形ABCD∽矩形A'B'C'D'.
A B C D
小结:判断两个图形是否相似,就是看它们是不是形状相同,与大小、位置无关.
5.【例1】下列图形中有可能与已知图形相似的是( )
C
小结:比例的基本运算,熟练比例式与乘积式的快速转化.
6.【例2】(北师9上P78)已知线段a,b,c,d,如果ab=cd,那么下列式子一定正确的是( )
A. B.
C. D.
C
7.【例3】(人教9下P26改编、北师9上P88改编)如图,四边形ABCD∽四边形A'B'C'D',求边x,y的长度和α的大小.
小结:解题关键是仔细观察图形,找准对应边和对应角,并根据相似多边形的对应角相等、对应边成比例,列算式或方程求解.
解:∵四边形ABCD∽四边形A'B'C'D',
∴,∠C=α,∠D=∠D'=140°,
∴x=12,y=,α=∠C=360°-∠A-∠B-∠D=360°-62°-75°-140°=83°.
小结:能根据相似得出比例式是解此题的关键.
8.【例4】如图,在矩形ABCD中,AB=4,BC=10,点E,F分别在AD,BC上,若矩形ABFE∽矩形BCDA,则BF的长为 .
1.6
9.(人教9下P27改编、北师9上P119改编)已知甲、乙两地的实际距离是20 km,在比例尺为1∶500 000的地图上甲、乙两地的距离是( )
A.40 cm B.400 cm
C.0.4 cm D.4 cm
D
10.(人教9下P26)如图,四边形ABCD∽四边形EFGH,求α,β的大小和EH的长度.
解:∵四边形ABCD∽四边形EFGH,
∴α=∠B=83°,∠D=∠H=118°,,
∴β=360°-(83°+78°+118°)=81°,,∴EH=28.
∴α=83°,β=81°,EH的长度为28 cm.
★11. 0.45 (创新题)如图,在矩形ABCD中,AB=1,AD>AB,在BC上取一点E,沿AE将△ABE向上折叠,使点B落在AD上的点F,若四边形EFDC与原矩形相似,则AD的长度为 .
请完成本节课后对应习题
布置作业
谢谢大家观看
人教版九年级数学下册课件
第二十七章 相似
27.1 图形的相似
课时2 相似多边形
1.理解相似多边形的定义.
2.能根据多边形相似进行相关的计算,会根据条件判断两个多边形是否相似.(重点、难点)
3.在学习相似图形的过程中,提高对相似图形中的对应关系的认识,增强数学推理能力.
学习目标
新课导入
情景导入
怎样从数学的角度刻画“形状相同”呢?这节课就让我们一起来探究相似多边形吧!
相似!
形状相同的两个多边形相似吗?
新课讲解
知识点1 相似多边形与相似比
A1
B1
C1
D1
E1
F1
A
B
C
D
E
F
多边形 ABCDEF 是显示在电脑屏幕上的,而多边形 A1B1C1D1E1F1 是投射到银幕上的.
新课讲解
问题1 这两个多边形相似吗?
问题2 在这两个多边形中,是否有对应相等的内角?
问题3 在这两个多边形中,夹相等内角的两边否成比例?
A1
B1
C1
D1
E1
F1
A
B
C
D
E
F
新课讲解
结论
相似多边形的定义:
各角分别相等、各边成比例的两个多边形叫做相似多边形.
相似多边形的特征:
相似多边形的对应角相等,对应边成比例.
相似比:
相似多边形的对应边的比叫作相似比.
新课讲解
任意两个等边三角形相似吗?任意两个正方形呢?任意两个正 n 边形呢?
a1
a2
a3
an
…
分析:已知等边三角形的每个角都为60°, 三边都相等. 所以满足边数相等,对应角相等,以及对应边的比相等.
新课讲解
同理,任意两个正方形都相似.
归纳:任意两个边数相等的正多边形都相似.
…
a1
a2
a3
an
新课讲解
活学巧记
两个相似多边形,边数相同形状同;
各角对应都相等,各边对应成比例.
(1)相似多边形的定义可用来判定两个多边形是否相似.
(2)相似多边形的性质常用来求相似多边形未知边的长度或未知角的度数.
课堂小结
相似多边形
概念
相似比
性质
对应角相等
对应边成比例
当堂小练
1. 填空:
(1) 如图①是两个相似的四边
形,则x= ,y = ,
α= ;
(2) 如图②是两个相似的矩形,
x= .
╰
65°
╯
80°
α
╭
6
125°
╯
80°
╮
3
x
y
图①
3
5
30
20
15
x
图②
2.5
1.5
90°
22.5
当堂小练
2. 如图所示的两个四边形是否相似?
答案:不相似.
∵四边形ABCD∽四边形A'B'C'D',
∴∠A= ,∠B= ,∠C= ,
∠D= ,= = .
∠D'
∠C'
∠B'
相似多边形的性质
∠A'
(1)对应角 ,对应边的比 .
(2)几何语言(以四边形为例):如图,
相等
相等
知识点
3.(人教9下P27改编)如图,△ABC∽△DEF,∠C=∠F=35°,∠B=115°,则x= ,y= ,∠D= °.
30
3.5
6
(1)如果两个多边形的对应角 ,且 相等,那么这两个多边形相似.
(2)几何语言(以四边形为例):如知识点3的图,
∵ ,
且 ,
∴ .
(3)相似多边形 的比叫做相似比,记作k.
对应边
四边形ABCD∽四边形A'B'C'D'
∠A=∠A',∠B=∠B',∠C=∠C',∠D=∠D'
对应边的比
相似多边形的判定(定义法)
相等
4.两个矩形的边长如图所示.
(1)求证:矩形ABCD∽矩形A'B'C'D';
(2)在(1)中,相似比= .
(1)证明:在矩形ABCD和矩形A'B'C'D'中,
∵∠A=∠A'=90°,∠B=∠B'=90°,
∠C=∠C'=90°,∠D=∠D'=90°,
,
∴矩形ABCD∽矩形A'B'C'D'.
A B C D
小结:判断两个图形是否相似,就是看它们是不是形状相同,与大小、位置无关.
5.【例1】下列图形中有可能与已知图形相似的是( )
C
小结:比例的基本运算,熟练比例式与乘积式的快速转化.
6.【例2】(北师9上P78)已知线段a,b,c,d,如果ab=cd,那么下列式子一定正确的是( )
A. B.
C. D.
C
7.【例3】(人教9下P26改编、北师9上P88改编)如图,四边形ABCD∽四边形A'B'C'D',求边x,y的长度和α的大小.
小结:解题关键是仔细观察图形,找准对应边和对应角,并根据相似多边形的对应角相等、对应边成比例,列算式或方程求解.
解:∵四边形ABCD∽四边形A'B'C'D',
∴,∠C=α,∠D=∠D'=140°,
∴x=12,y=,α=∠C=360°-∠A-∠B-∠D=360°-62°-75°-140°=83°.
小结:能根据相似得出比例式是解此题的关键.
8.【例4】如图,在矩形ABCD中,AB=4,BC=10,点E,F分别在AD,BC上,若矩形ABFE∽矩形BCDA,则BF的长为 .
1.6
9.(人教9下P27改编、北师9上P119改编)已知甲、乙两地的实际距离是20 km,在比例尺为1∶500 000的地图上甲、乙两地的距离是( )
A.40 cm B.400 cm
C.0.4 cm D.4 cm
D
10.(人教9下P26)如图,四边形ABCD∽四边形EFGH,求α,β的大小和EH的长度.
解:∵四边形ABCD∽四边形EFGH,
∴α=∠B=83°,∠D=∠H=118°,,
∴β=360°-(83°+78°+118°)=81°,,∴EH=28.
∴α=83°,β=81°,EH的长度为28 cm.
★11. 0.45 (创新题)如图,在矩形ABCD中,AB=1,AD>AB,在BC上取一点E,沿AE将△ABE向上折叠,使点B落在AD上的点F,若四边形EFDC与原矩形相似,则AD的长度为 .
请完成本节课后对应习题
布置作业
谢谢大家观看
