2024-2025学年北师大版八年级数学下册课件1.2直角三角形课时2 直角三角形全等的判定(共34张PPT)
文档属性
| 名称 | 2024-2025学年北师大版八年级数学下册课件1.2直角三角形课时2 直角三角形全等的判定(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-05 20:42:23 | ||
图片预览









文档简介
(共34张PPT)
第一章 三角形的证明
1.2 直角三角形
课时2 直角三角形全等的判定
判定两直角三角形全等的方法
判断两三角形全等方法的综合应用.(重点、难点)
学习目标
新课讲解
知识点1 判定两直角三角形全等的方法
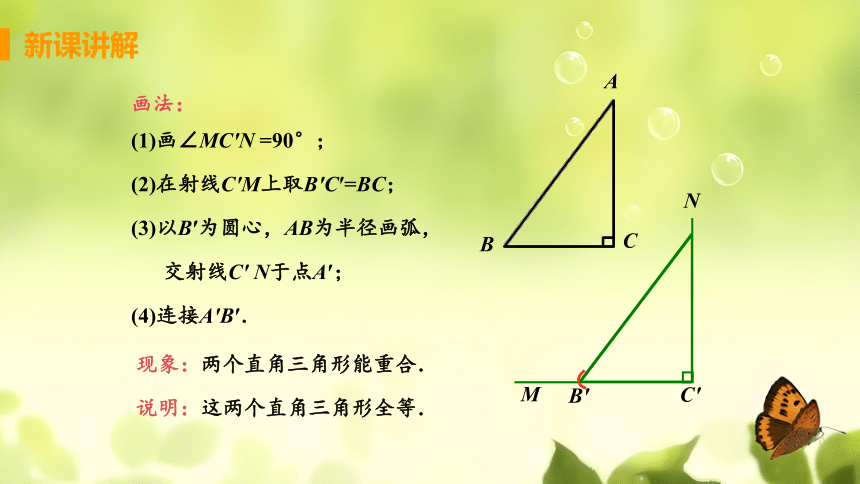
问题 任意画一个Rt△ABC,使∠C =90°,再
画一个Rt△A′B′C′,使∠C′=90°,B′C′=BC,
A′B′=AB,然后把画好的Rt△A′B′C′剪下来放到
Rt△ABC上,你发现了什么?
新课讲解
A
B
C
(1)画∠MC′N =90°;
(2)在射线C′M上取B′C′=BC;
(3)以B′为圆心,AB为半径画弧,
交射线C′ N于点A′;
(4)连接A′B′.
现象:两个直角三角形能重合.
说明:这两个直角三角形全等.
画法:
N
M
C′
B′
新课讲解
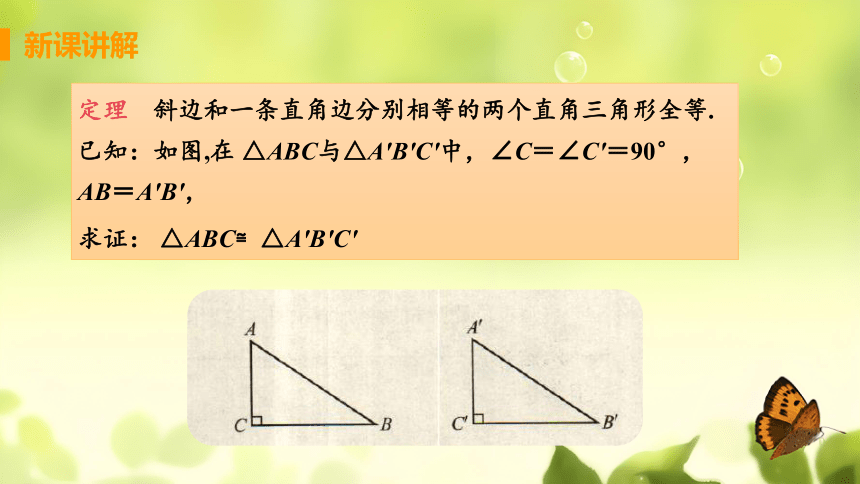
定理 斜边和一条直角边分别相等的两个直角三角形全等.
已知:如图,在 △ABC与△A′B′C′中,∠C=∠C′=90°,AB=A′B′,
求证: △ABC≌△A′B′C′
新课讲解
在△ABC中,
∵∠C= 90°,
∴BC2= AB2-AC2 (勾股定理).
同理, B′C′ 2=A′B′2-A′C′ 2.
∵AB=A′B′, AC=A′C′,
∴BC=B′C′.
∴ △ABC≌△A′B′C′(SSS).
证明:
新课讲解
1.斜边和一条直角边分别相等的两个直角三角形全等(简
写成“斜边、直角边”或“HL”).
2.(1)书写格式:如图,在Rt△ABC和Rt△A′B′C′中,
∴Rt△ABC≌Rt△A′B′C′.
(2)注意点:书写时必须强调直
角三角形.
新课讲解
练一练
1.如图,两根长度均为12 m的绳子,一端系在旗杆上,另一端分别固定在地面的两个木粧上,两个木桩离旗 杆底部的距离相等吗?请说明你的理由.
两个木桩离旗杆底部的距离相等.
理由如下:在Rt△ABO和Rt△ACO中,
所以Rt△ABO≌Rt△ACO(HL).
所以BO=CO.
故两个木桩离旗杆底部的距离相等.
解:
新课讲解
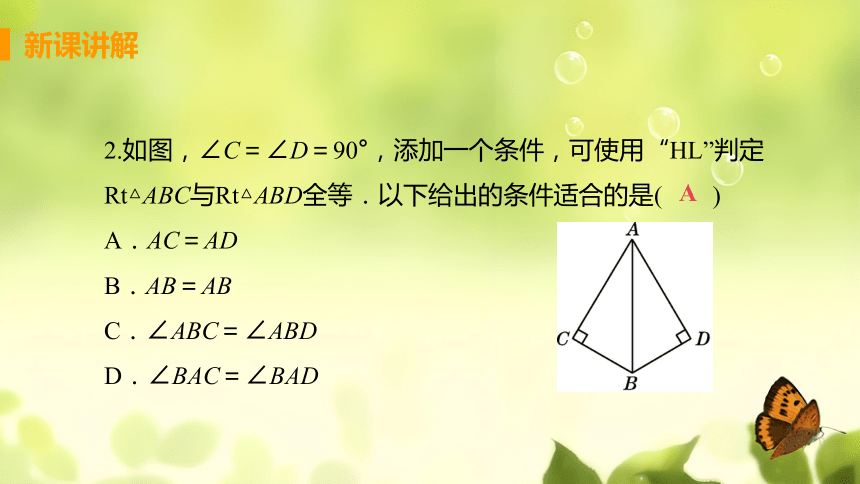
2.如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是( )
A.AC=AD
B.AB=AB
C.∠ABC=∠ABD
D.∠BAC=∠BAD
A
新课讲解
知识点2 判断两三角形全等方法的综合应用
直角三角形全等的判定既可以用“SSS” “SAS”
“ASA”和“AAS”,有可以用 “HL”.
新课讲解
证明两个三角形全等,一般情况下是已知两个条
件去找第三个全等条件,有以下几种情况:
(4)已知一边及其对角,只能找任意一角.
新课讲解
练一练
判断下列命题的真假,并说明理由:
(1)两个锐角分别相等的两个直角三角形全等;
(2)两条直角边分别相等的两个直角三角形全等;
(3)一条直角边相等且另一条直角边上的中线相
等的两个直角三角形全等.
新课讲解
(1)假.理由:如图,
在Rt△ABC和Rt△AB′C′中,
∠A=∠A,∠AB′C′=∠ABC,
但Rt△ABC与Rt△AB′C′不全等.
(2)真.理由:因为该命题满足“AAS”公理的条件.
(3)真.理由:因为该命题满足“SAS”公理的条件.
(4)真.先利用“HL”定理得到另一条直角边的一半
相等,也即该直角边相等,再根据“SAS”公理可
判定两个三角形全等.
解:
课堂小结
1.直角三角形的判定方法:
边边边、边角边、角边角、角角边、
斜边、直角边.
2. 判定直角三角形全等的“四种思路”:
(1)若已知条件中有一组直角边和一组斜边分别相等,用“HL”判定.
(2)若有一组锐角和斜边分别相等,用“AAS”判定.
(3)若有一组锐角和一组直角边分别相等,
①直角边是锐角的对边,用“AAS”判定;
②直角边是锐角的邻边,用“ASA”判定.
(4)若有两组直角边分别相等,用“SAS”判定.
当堂小练
1.如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=4,则下列各图中的直角三角形与Rt△ABC全等的是( )
A
当堂小练
2.如图,在△ABC中,AD⊥BC,D为BC的中点,以下结论:①△ABD≌△ACD;②AB=AC;③∠B=∠C;④AD是△ABC的角平分线.
其中正确的有( )
A.1个
B.2个
C.3个
D.4个
D
拓展与延伸
如图,AD,BC相交于点O,AD=BC,∠C=∠D=90°,
(1)求证:△ACB≌△BDA;
(2)若∠ABC=35°,
则∠CAO=________.
20°
拓展与延伸
∵∠C=∠D=90°,
∴△ACB和△BDA都是直角三角形.
在Rt△ACB和Rt△BDA中,
BC=AD,
AB=BA,
∴Rt△ACB≌Rt△BDA.
(1)证明:
(1) 和一条 分别相等的两个直角三角形全等.简述为“斜边、直角边”或“ ”定理.
(2)几何语言:
如图,在Rt△ABC和Rt△A'B'C'中,
∴Rt△ABC≌ ( ).
“斜边、直角边”定理(HL)
斜边
直角边
HL
Rt△A'B'C'
HL
1.(1)如图,可用“HL”直接判定Rt△ABC和Rt△A'B'C'全等的条件是( )
A.AC=A'C',BC=B'C' B.∠A=∠A',AB=A'B'
C.AC=A'C',AB=A'B' D.∠B=∠B',BC=B'C'
C
(2)如图,在△ABC中,AD⊥BC于D,要使△ABD≌△ACD,若根据HL直接判定,还需要添加的一个条件是 .
AB=AC
可以判定直角三角形全等的方法有: .
例:如图,在Rt△ABC和Rt△DEF中,∠C=∠F=90°.请据此解答对点训练第2题.
直角三角形全等的判定方法
HL,AAS,SAS,ASA,SSS
2.见知识点2中的示例及图,完成下列问题:
(1)若∠A=∠D,BC=EF,则Rt△ABC≌Rt△DEF的依据是 ;
(2)若∠A=∠D,AC=DF,则Rt△ABC≌Rt△DEF的依据是 ;
(3)若∠A=∠D,AB=DE,则Rt△ABC≌Rt△DEF的依据是 ;
(4)若AC=DF,AB=DE,则Rt△ABC≌Rt△DEF的依据是 ;
(5)若AC=DF,CB=FE,则Rt△ABC≌Rt△DEF的依据是 .
AAS
ASA
AAS
HL
SAS
例:如图,AB⊥AC,DC⊥AC,AD=BC,则根据 判定方法,可得△ ≌△ .
应用直角三角形全等的判定与性质解决问题
ABC
HL
CDA
3.如图,AC⊥BC,AD⊥BD,AC=AD.
求证:CB=DB.
证明:∵AC⊥BC,AD⊥BD,∴∠C=∠D=90°.
在Rt△ACB和Rt△ADB中, ,
∴Rt△ACB≌Rt△ADB(HL).∴CB=DB.
4.【例1】(2024郑州期中)如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还要添加的一个条件是
( )
A.AB=DC
B.∠A=∠D
C.∠B=∠C
D.AE=DF
A
5.【例2】(北师8下P34、人教8上P44)如图,BD,CE是△ABC的高,且BE=CD,求证:△ABC是等腰三角形.
证明:∵BD,CE是△ABC的高,
∴∠BEC=∠CDB=90°.
在Rt△BEC和Rt△CDB中,,
∴Rt△BEC≌Rt△CDB(HL).
∴∠ABC=∠ACB.∴AB=AC.
∴△ABC是等腰三角形.
6.如图,AB=AC,BE⊥AC于E,CF⊥AB于F,BE,CF交于点D,则下列结论中不正确的是( )
A.△ABE≌△ACF
B.点D在∠BAC的平分线上
C.△BDF≌△CDE
D.点D是BE的中点
D
【提示:连接AD,证明△ADE≌△ADF】
7.(北师8下P21、人教8上P51)用三角尺可按下面方法画角平分线:在已知的∠AOB的两边上,分别取OM=ON,再分别过点M,N作OA,OB的垂线,交点为P,画射线OP,则OP平分∠AOB.为什么?
解:理由如下:
∵OM⊥MP,ON⊥NP,∴∠OMP=∠ONP=90°,
在Rt△OMP和Rt△ONP中,,
∴Rt△OMP≌Rt△ONP(HL),
∴∠MOP=∠NOP,∴OP平分∠AOB.
★8. 【问题初识】(1)如图1,AB⊥AD,ED⊥AD,AB=CD,AC=DE,求证:BC⊥CE;
【拓展探究】(2)如图2,AB⊥AD,ED⊥AD,AB=CD,AD=DE,探索BD⊥CE的结论是否成立,并说明理由.
0.45
图1 图2
(1)证明:∵AB⊥AD,ED⊥AD,
∴∠A=∠D=90°.
又∵AB=CD,AC=DE,
∴△ABC≌△DCE.∴∠B=∠DCE.
∵∠B+∠ACB=90°,
∴∠ACB+∠DCE=90°.
∴∠BCE=90°,即BC⊥CE.
(2)解:BD⊥CE成立.理由如下:设BD与EC交于点F,
∵AB⊥AD,ED⊥AD,
∴∠A=∠CDE=90°.
又∵AB=CD,AD=DE,
∴△ABD≌△DCE.∴∠B=∠DCE.
∵∠B+∠ADB=90°,
∴∠ADB+∠DCE=90°.
∴∠CFD=90°,即BD⊥CE.
备注:每课时带★的题目为提高题.(难度系数越小,题目越难)
请完成本节课后对应习题
布置作业
第一章 三角形的证明
1.2 直角三角形
课时2 直角三角形全等的判定
判定两直角三角形全等的方法
判断两三角形全等方法的综合应用.(重点、难点)
学习目标
新课讲解
知识点1 判定两直角三角形全等的方法
问题 任意画一个Rt△ABC,使∠C =90°,再
画一个Rt△A′B′C′,使∠C′=90°,B′C′=BC,
A′B′=AB,然后把画好的Rt△A′B′C′剪下来放到
Rt△ABC上,你发现了什么?
新课讲解
A
B
C
(1)画∠MC′N =90°;
(2)在射线C′M上取B′C′=BC;
(3)以B′为圆心,AB为半径画弧,
交射线C′ N于点A′;
(4)连接A′B′.
现象:两个直角三角形能重合.
说明:这两个直角三角形全等.
画法:
N
M
C′
B′
新课讲解
定理 斜边和一条直角边分别相等的两个直角三角形全等.
已知:如图,在 △ABC与△A′B′C′中,∠C=∠C′=90°,AB=A′B′,
求证: △ABC≌△A′B′C′
新课讲解
在△ABC中,
∵∠C= 90°,
∴BC2= AB2-AC2 (勾股定理).
同理, B′C′ 2=A′B′2-A′C′ 2.
∵AB=A′B′, AC=A′C′,
∴BC=B′C′.
∴ △ABC≌△A′B′C′(SSS).
证明:
新课讲解
1.斜边和一条直角边分别相等的两个直角三角形全等(简
写成“斜边、直角边”或“HL”).
2.(1)书写格式:如图,在Rt△ABC和Rt△A′B′C′中,
∴Rt△ABC≌Rt△A′B′C′.
(2)注意点:书写时必须强调直
角三角形.
新课讲解
练一练
1.如图,两根长度均为12 m的绳子,一端系在旗杆上,另一端分别固定在地面的两个木粧上,两个木桩离旗 杆底部的距离相等吗?请说明你的理由.
两个木桩离旗杆底部的距离相等.
理由如下:在Rt△ABO和Rt△ACO中,
所以Rt△ABO≌Rt△ACO(HL).
所以BO=CO.
故两个木桩离旗杆底部的距离相等.
解:
新课讲解
2.如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是( )
A.AC=AD
B.AB=AB
C.∠ABC=∠ABD
D.∠BAC=∠BAD
A
新课讲解
知识点2 判断两三角形全等方法的综合应用
直角三角形全等的判定既可以用“SSS” “SAS”
“ASA”和“AAS”,有可以用 “HL”.
新课讲解
证明两个三角形全等,一般情况下是已知两个条
件去找第三个全等条件,有以下几种情况:
(4)已知一边及其对角,只能找任意一角.
新课讲解
练一练
判断下列命题的真假,并说明理由:
(1)两个锐角分别相等的两个直角三角形全等;
(2)两条直角边分别相等的两个直角三角形全等;
(3)一条直角边相等且另一条直角边上的中线相
等的两个直角三角形全等.
新课讲解
(1)假.理由:如图,
在Rt△ABC和Rt△AB′C′中,
∠A=∠A,∠AB′C′=∠ABC,
但Rt△ABC与Rt△AB′C′不全等.
(2)真.理由:因为该命题满足“AAS”公理的条件.
(3)真.理由:因为该命题满足“SAS”公理的条件.
(4)真.先利用“HL”定理得到另一条直角边的一半
相等,也即该直角边相等,再根据“SAS”公理可
判定两个三角形全等.
解:
课堂小结
1.直角三角形的判定方法:
边边边、边角边、角边角、角角边、
斜边、直角边.
2. 判定直角三角形全等的“四种思路”:
(1)若已知条件中有一组直角边和一组斜边分别相等,用“HL”判定.
(2)若有一组锐角和斜边分别相等,用“AAS”判定.
(3)若有一组锐角和一组直角边分别相等,
①直角边是锐角的对边,用“AAS”判定;
②直角边是锐角的邻边,用“ASA”判定.
(4)若有两组直角边分别相等,用“SAS”判定.
当堂小练
1.如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=4,则下列各图中的直角三角形与Rt△ABC全等的是( )
A
当堂小练
2.如图,在△ABC中,AD⊥BC,D为BC的中点,以下结论:①△ABD≌△ACD;②AB=AC;③∠B=∠C;④AD是△ABC的角平分线.
其中正确的有( )
A.1个
B.2个
C.3个
D.4个
D
拓展与延伸
如图,AD,BC相交于点O,AD=BC,∠C=∠D=90°,
(1)求证:△ACB≌△BDA;
(2)若∠ABC=35°,
则∠CAO=________.
20°
拓展与延伸
∵∠C=∠D=90°,
∴△ACB和△BDA都是直角三角形.
在Rt△ACB和Rt△BDA中,
BC=AD,
AB=BA,
∴Rt△ACB≌Rt△BDA.
(1)证明:
(1) 和一条 分别相等的两个直角三角形全等.简述为“斜边、直角边”或“ ”定理.
(2)几何语言:
如图,在Rt△ABC和Rt△A'B'C'中,
∴Rt△ABC≌ ( ).
“斜边、直角边”定理(HL)
斜边
直角边
HL
Rt△A'B'C'
HL
1.(1)如图,可用“HL”直接判定Rt△ABC和Rt△A'B'C'全等的条件是( )
A.AC=A'C',BC=B'C' B.∠A=∠A',AB=A'B'
C.AC=A'C',AB=A'B' D.∠B=∠B',BC=B'C'
C
(2)如图,在△ABC中,AD⊥BC于D,要使△ABD≌△ACD,若根据HL直接判定,还需要添加的一个条件是 .
AB=AC
可以判定直角三角形全等的方法有: .
例:如图,在Rt△ABC和Rt△DEF中,∠C=∠F=90°.请据此解答对点训练第2题.
直角三角形全等的判定方法
HL,AAS,SAS,ASA,SSS
2.见知识点2中的示例及图,完成下列问题:
(1)若∠A=∠D,BC=EF,则Rt△ABC≌Rt△DEF的依据是 ;
(2)若∠A=∠D,AC=DF,则Rt△ABC≌Rt△DEF的依据是 ;
(3)若∠A=∠D,AB=DE,则Rt△ABC≌Rt△DEF的依据是 ;
(4)若AC=DF,AB=DE,则Rt△ABC≌Rt△DEF的依据是 ;
(5)若AC=DF,CB=FE,则Rt△ABC≌Rt△DEF的依据是 .
AAS
ASA
AAS
HL
SAS
例:如图,AB⊥AC,DC⊥AC,AD=BC,则根据 判定方法,可得△ ≌△ .
应用直角三角形全等的判定与性质解决问题
ABC
HL
CDA
3.如图,AC⊥BC,AD⊥BD,AC=AD.
求证:CB=DB.
证明:∵AC⊥BC,AD⊥BD,∴∠C=∠D=90°.
在Rt△ACB和Rt△ADB中, ,
∴Rt△ACB≌Rt△ADB(HL).∴CB=DB.
4.【例1】(2024郑州期中)如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还要添加的一个条件是
( )
A.AB=DC
B.∠A=∠D
C.∠B=∠C
D.AE=DF
A
5.【例2】(北师8下P34、人教8上P44)如图,BD,CE是△ABC的高,且BE=CD,求证:△ABC是等腰三角形.
证明:∵BD,CE是△ABC的高,
∴∠BEC=∠CDB=90°.
在Rt△BEC和Rt△CDB中,,
∴Rt△BEC≌Rt△CDB(HL).
∴∠ABC=∠ACB.∴AB=AC.
∴△ABC是等腰三角形.
6.如图,AB=AC,BE⊥AC于E,CF⊥AB于F,BE,CF交于点D,则下列结论中不正确的是( )
A.△ABE≌△ACF
B.点D在∠BAC的平分线上
C.△BDF≌△CDE
D.点D是BE的中点
D
【提示:连接AD,证明△ADE≌△ADF】
7.(北师8下P21、人教8上P51)用三角尺可按下面方法画角平分线:在已知的∠AOB的两边上,分别取OM=ON,再分别过点M,N作OA,OB的垂线,交点为P,画射线OP,则OP平分∠AOB.为什么?
解:理由如下:
∵OM⊥MP,ON⊥NP,∴∠OMP=∠ONP=90°,
在Rt△OMP和Rt△ONP中,,
∴Rt△OMP≌Rt△ONP(HL),
∴∠MOP=∠NOP,∴OP平分∠AOB.
★8. 【问题初识】(1)如图1,AB⊥AD,ED⊥AD,AB=CD,AC=DE,求证:BC⊥CE;
【拓展探究】(2)如图2,AB⊥AD,ED⊥AD,AB=CD,AD=DE,探索BD⊥CE的结论是否成立,并说明理由.
0.45
图1 图2
(1)证明:∵AB⊥AD,ED⊥AD,
∴∠A=∠D=90°.
又∵AB=CD,AC=DE,
∴△ABC≌△DCE.∴∠B=∠DCE.
∵∠B+∠ACB=90°,
∴∠ACB+∠DCE=90°.
∴∠BCE=90°,即BC⊥CE.
(2)解:BD⊥CE成立.理由如下:设BD与EC交于点F,
∵AB⊥AD,ED⊥AD,
∴∠A=∠CDE=90°.
又∵AB=CD,AD=DE,
∴△ABD≌△DCE.∴∠B=∠DCE.
∵∠B+∠ADB=90°,
∴∠ADB+∠DCE=90°.
∴∠CFD=90°,即BD⊥CE.
备注:每课时带★的题目为提高题.(难度系数越小,题目越难)
请完成本节课后对应习题
布置作业
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
