【备课无忧】人教版五下-2.1 因数和倍数(教学设计含反思)
文档属性
| 名称 | 【备课无忧】人教版五下-2.1 因数和倍数(教学设计含反思) | 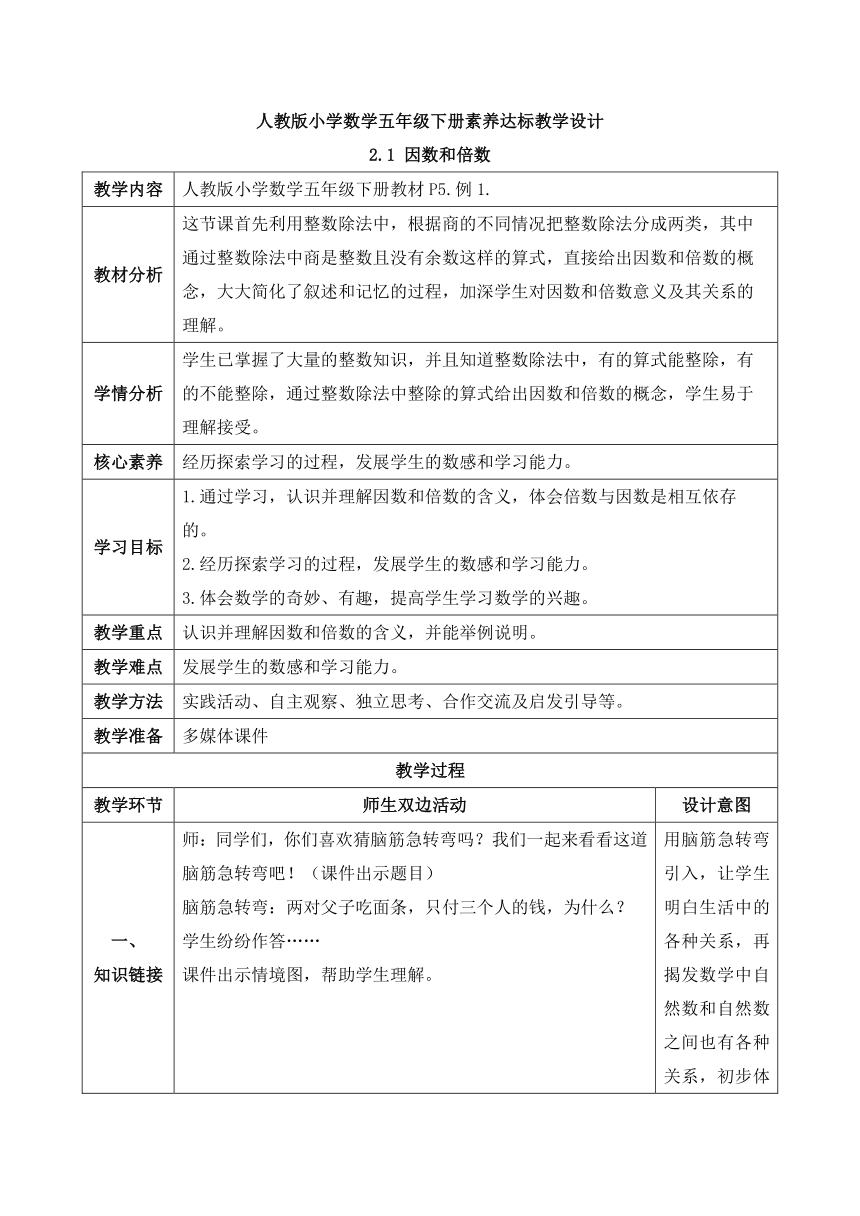 | |
| 格式 | docx | ||
| 文件大小 | 271.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-05 11:04:00 | ||
图片预览


文档简介
人教版小学数学五年级下册素养达标教学设计
2.1 因数和倍数
教学内容 人教版小学数学五年级下册教材P5.例1.
教材分析 这节课首先利用整数除法中,根据商的不同情况把整数除法分成两类,其中通过整数除法中商是整数且没有余数这样的算式,直接给出因数和倍数的概念,大大简化了叙述和记忆的过程,加深学生对因数和倍数意义及其关系的理解。
学情分析 学生已掌握了大量的整数知识,并且知道整数除法中,有的算式能整除,有的不能整除,通过整数除法中整除的算式给出因数和倍数的概念,学生易于理解接受。
核心素养 经历探索学习的过程,发展学生的数感和学习能力。
学习目标 1.通过学习,认识并理解因数和倍数的含义,体会倍数与因数是相互依存的。 2.经历探索学习的过程,发展学生的数感和学习能力。 3.体会数学的奇妙、有趣,提高学生学习数学的兴趣。
教学重点 认识并理解因数和倍数的含义,并能举例说明。
教学难点 发展学生的数感和学习能力。
教学方法 实践活动、自主观察、独立思考、合作交流及启发引导等。
教学准备 多媒体课件
教学过程
教学环节 师生双边活动 设计意图
一、 知识链接 师:同学们,你们喜欢猜脑筋急转弯吗?我们一起来看看这道脑筋急转弯吧!(课件出示题目) 脑筋急转弯:两对父子吃面条,只付三个人的钱,为什么? 学生纷纷作答…… 课件出示情境图,帮助学生理解。 师总结:不能单独说谁是爸爸,谁是儿子。 师:在数学中,数与数之间也存在着多种关系,这节课,我们一起来探讨两数之间的因数与倍数关系。 用脑筋急转弯引入,让学生明白生活中的各种关系,再揭发数学中自然数和自然数之间也有各种关系,初步体会数与数的对应关系,这样既能让学生感受数学和生活中的密切联系,又能激发学生的学习兴趣,提高学生主动学习探究学习的积极性。
二、 探究新知 1.因数、倍数的意义 例1.在前面的学习中,我们知道两个整数相除,结果有下面两种情况。 (1)明确因数和倍数的意义 师提问:你们知道为什么这么分类吗? 生:第一种的商是整数而没有余数,第二种的商有余数。 课件出示概念:在整数除法中,如果商是整数且没有余数,我们就说被除数是除数的倍数,除数是被除数的因数。 (2)举例说明因数和倍数的关系 师:例如,12÷2=6,我们就说2是12的因数,12是2的倍数。 师提问:12÷6=2中,谁是谁的倍数,谁是谁的因数? 生:6是12的因数,12是6的倍数。 师提问:2×6=12中,谁是谁的倍数,谁是谁的因数? 生:12是2和6的倍数,2和6是12的因数。 教师组织学生同桌合作:说一说,上面第一种情况的每个算式中,谁是谁的因数?谁是谁的倍数? 学生汇报: ①在20÷10=2中,10和2是20的因数,20是10和2的倍数。 ②在30÷6=5中,6和5是30的因数,30是6和5的倍数。 ③在21÷21=1中,21和1是21的因数,21是21和1的倍数。 ④在63÷9=7中,9和7是63的因数,63是9和7的倍数。 (3)因数和倍数的依存性 思考:下面说法正确吗? 生:不正确。 师总结:因数和倍数是相互依存的,它们都不能单独存在,不能说谁的倍数,谁是因数,应该说谁是谁的倍数,谁是谁的因数。 (4)明确0的特殊性 思考:在6.3÷9=0.7中,6.3是9的倍数,9是6.3的因数。这个说法正确吗? 生:不正确。 师总结:对的,因数和倍数的条件:被除数、除数和商都是大于0的自然数。 注意:为了方便,在研究的因数和倍数时候,我们所指的数是自然数(一般不包括0)。 2.小结 (1)在整数除法中,如果商是整数且没有余数(或者说余数为0),我们就说除数是被除数的因数(也称约数),被除数是除数的倍数。 (2)字母表示:如果a÷b=c(a,b,c是非0自然数),那么b、c就是a的因数,a就是b、c的倍数。 结合除法算式帮助学生更好地理解因数和倍数的概念,再让学生通过自主学习、合作交流等过程完成对因数与倍数的认识,从而体验自主学习的快乐。通过两个判断题,引导学生理解因数与倍数的依存性和0的特殊性,帮助学生全面认识因数与倍数。
三、 课堂演练 一、判断题。 1.因为21÷3=7,所以21是倍数,3是因数。 ( × ) 2.因为6÷1.2=5,6是1.2的倍数,1.2是6的因数。( × ) 3.25是5的倍数,5是25的因数。 ( √ ) 4.如果m÷n=8,那么n是m的因数,m是n的倍数。( × ) 二、选择题。 5.已知a是41的因数,那么a不可能是( C )。 A.1 B.41 C.0 6.能表示因数和倍数关系的等式是( B )。 A.8÷0.4=20 B.3×6=18 C.7×0=0 三、下面的4组数中,谁是谁的因数?谁是谁的倍数? (教材P5“做一做”) 4和24 26和13 75和25 81和9 因为24÷4=6,所以4是24的因数,24是4的倍数。 因为26÷13=2,所以13是26的因数,26是13的倍数。 因为75÷25=3,所以25是75的因数,75是25的倍数。 因为81÷9=9,所以9是81的因数,81是9的倍数。 主要是巩固课堂所学的知识,提升解决问题的能力。
四、 总结评价 1.课堂总结 2.素养评价 3.布置作业 (1)完成《分层作业》中对应练习。 (2)预习下一节内容。
板书设计
课后作业 1.完成《分层作业》中对应练习; 2.预习下一节内容。
课后反思 学生在前面已经接触过因数和倍数的概念,但是此“因数”“倍数”与彼“因数”“倍数”不是同一概念,学生还是有点容易混淆。由于本节课是学生建立因数和倍数概念的第一课时,为了能建立清晰正确的概念,避免造成不必要的干扰,教师回避了乘法各部分名称及“倍数”“几倍”,计划等学生对因数和倍数有了较全面的认识后再来辨析。
2.1 因数和倍数
教学内容 人教版小学数学五年级下册教材P5.例1.
教材分析 这节课首先利用整数除法中,根据商的不同情况把整数除法分成两类,其中通过整数除法中商是整数且没有余数这样的算式,直接给出因数和倍数的概念,大大简化了叙述和记忆的过程,加深学生对因数和倍数意义及其关系的理解。
学情分析 学生已掌握了大量的整数知识,并且知道整数除法中,有的算式能整除,有的不能整除,通过整数除法中整除的算式给出因数和倍数的概念,学生易于理解接受。
核心素养 经历探索学习的过程,发展学生的数感和学习能力。
学习目标 1.通过学习,认识并理解因数和倍数的含义,体会倍数与因数是相互依存的。 2.经历探索学习的过程,发展学生的数感和学习能力。 3.体会数学的奇妙、有趣,提高学生学习数学的兴趣。
教学重点 认识并理解因数和倍数的含义,并能举例说明。
教学难点 发展学生的数感和学习能力。
教学方法 实践活动、自主观察、独立思考、合作交流及启发引导等。
教学准备 多媒体课件
教学过程
教学环节 师生双边活动 设计意图
一、 知识链接 师:同学们,你们喜欢猜脑筋急转弯吗?我们一起来看看这道脑筋急转弯吧!(课件出示题目) 脑筋急转弯:两对父子吃面条,只付三个人的钱,为什么? 学生纷纷作答…… 课件出示情境图,帮助学生理解。 师总结:不能单独说谁是爸爸,谁是儿子。 师:在数学中,数与数之间也存在着多种关系,这节课,我们一起来探讨两数之间的因数与倍数关系。 用脑筋急转弯引入,让学生明白生活中的各种关系,再揭发数学中自然数和自然数之间也有各种关系,初步体会数与数的对应关系,这样既能让学生感受数学和生活中的密切联系,又能激发学生的学习兴趣,提高学生主动学习探究学习的积极性。
二、 探究新知 1.因数、倍数的意义 例1.在前面的学习中,我们知道两个整数相除,结果有下面两种情况。 (1)明确因数和倍数的意义 师提问:你们知道为什么这么分类吗? 生:第一种的商是整数而没有余数,第二种的商有余数。 课件出示概念:在整数除法中,如果商是整数且没有余数,我们就说被除数是除数的倍数,除数是被除数的因数。 (2)举例说明因数和倍数的关系 师:例如,12÷2=6,我们就说2是12的因数,12是2的倍数。 师提问:12÷6=2中,谁是谁的倍数,谁是谁的因数? 生:6是12的因数,12是6的倍数。 师提问:2×6=12中,谁是谁的倍数,谁是谁的因数? 生:12是2和6的倍数,2和6是12的因数。 教师组织学生同桌合作:说一说,上面第一种情况的每个算式中,谁是谁的因数?谁是谁的倍数? 学生汇报: ①在20÷10=2中,10和2是20的因数,20是10和2的倍数。 ②在30÷6=5中,6和5是30的因数,30是6和5的倍数。 ③在21÷21=1中,21和1是21的因数,21是21和1的倍数。 ④在63÷9=7中,9和7是63的因数,63是9和7的倍数。 (3)因数和倍数的依存性 思考:下面说法正确吗? 生:不正确。 师总结:因数和倍数是相互依存的,它们都不能单独存在,不能说谁的倍数,谁是因数,应该说谁是谁的倍数,谁是谁的因数。 (4)明确0的特殊性 思考:在6.3÷9=0.7中,6.3是9的倍数,9是6.3的因数。这个说法正确吗? 生:不正确。 师总结:对的,因数和倍数的条件:被除数、除数和商都是大于0的自然数。 注意:为了方便,在研究的因数和倍数时候,我们所指的数是自然数(一般不包括0)。 2.小结 (1)在整数除法中,如果商是整数且没有余数(或者说余数为0),我们就说除数是被除数的因数(也称约数),被除数是除数的倍数。 (2)字母表示:如果a÷b=c(a,b,c是非0自然数),那么b、c就是a的因数,a就是b、c的倍数。 结合除法算式帮助学生更好地理解因数和倍数的概念,再让学生通过自主学习、合作交流等过程完成对因数与倍数的认识,从而体验自主学习的快乐。通过两个判断题,引导学生理解因数与倍数的依存性和0的特殊性,帮助学生全面认识因数与倍数。
三、 课堂演练 一、判断题。 1.因为21÷3=7,所以21是倍数,3是因数。 ( × ) 2.因为6÷1.2=5,6是1.2的倍数,1.2是6的因数。( × ) 3.25是5的倍数,5是25的因数。 ( √ ) 4.如果m÷n=8,那么n是m的因数,m是n的倍数。( × ) 二、选择题。 5.已知a是41的因数,那么a不可能是( C )。 A.1 B.41 C.0 6.能表示因数和倍数关系的等式是( B )。 A.8÷0.4=20 B.3×6=18 C.7×0=0 三、下面的4组数中,谁是谁的因数?谁是谁的倍数? (教材P5“做一做”) 4和24 26和13 75和25 81和9 因为24÷4=6,所以4是24的因数,24是4的倍数。 因为26÷13=2,所以13是26的因数,26是13的倍数。 因为75÷25=3,所以25是75的因数,75是25的倍数。 因为81÷9=9,所以9是81的因数,81是9的倍数。 主要是巩固课堂所学的知识,提升解决问题的能力。
四、 总结评价 1.课堂总结 2.素养评价 3.布置作业 (1)完成《分层作业》中对应练习。 (2)预习下一节内容。
板书设计
课后作业 1.完成《分层作业》中对应练习; 2.预习下一节内容。
课后反思 学生在前面已经接触过因数和倍数的概念,但是此“因数”“倍数”与彼“因数”“倍数”不是同一概念,学生还是有点容易混淆。由于本节课是学生建立因数和倍数概念的第一课时,为了能建立清晰正确的概念,避免造成不必要的干扰,教师回避了乘法各部分名称及“倍数”“几倍”,计划等学生对因数和倍数有了较全面的认识后再来辨析。
