【备课无忧】人教版五下-3.2 认识正方体(教学课件).pptx
文档属性
| 名称 | 【备课无忧】人教版五下-3.2 认识正方体(教学课件).pptx |

|
|
| 格式 | pptx | ||
| 文件大小 | 18.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-05 00:00:00 | ||
图片预览





文档简介
(共28张PPT)
人教版数学五年级下册
第
三
单
元
2.认识正方体
看图填空。
20 cm
10 cm
10 cm
(1)长方体有_____个面;_____条棱;_____个顶点。
(2)长方体有_____条长;_____条宽;_____条高。
(3)这个长方体的棱长总和是_______。
6
12
8
4
4
4
160 cm
(20+10+10)×4 = 160(cm)
按下面的方法将长方体平均成两份,得到的是什么呢?
你在生活中见过正方体吗?
正方体
正方体也叫立方体。
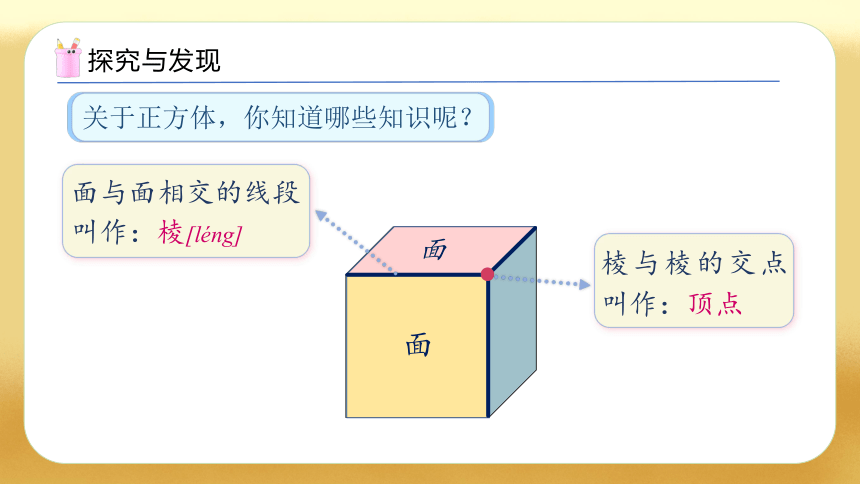
关于正方体,你知道哪些知识呢?
面
面
面与面相交的线段叫作:棱[léng]
棱与棱的交点叫作:顶点
交流互动:
拿一个正方体的物品来观察,并在小组内说一说你有什么发现?
6
完全相同的正方形
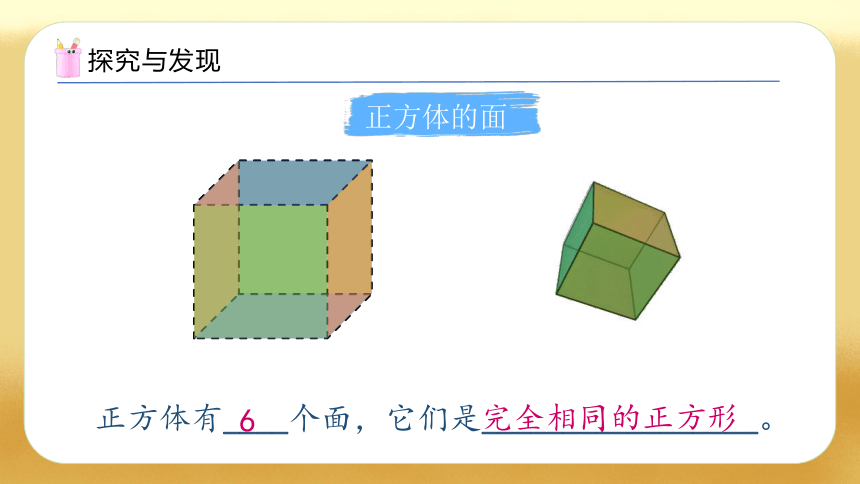
正方体的面
正方体有____个面,它们是_________________。
相对的棱互相______,相邻的棱互相______。
正方体有______条棱,它们_______________。
正方体的棱和顶点
12
长度都相等
平行
垂直
棱
棱
棱
正方体不需要用长、宽、高来区分。
正方体有8个顶点。
同桌合作:剪下本书附页中图2的图样做一个正方体,再量
出它的棱长是多少厘米。
0
1
2
3
4
5
3 cm
3×12 = 36(cm)
你能求出这个正方体的棱长总和吗?
正方体的棱长总和 = 棱长×12
长方体和长方体有哪些相同点?有哪些不同点?填入下表。
长方体 正方体
相同点 不同点
都有___个面、___条棱和___个顶点。
6 个面是长方形(特殊情况两个相对的面是正方形)
相对的面__________。
6 个面都是完全
相同的_______。
相对的棱的长度_____。
12条棱的长度都相等。
完全相同
正方形
相等
6
12
8
你能用集合的方式表示正方体和长方体的关系吗?
长方体
正方体
正方体是长、宽、高都相等的长方体。
【教材P20“做一做”】
1.用棱长1 cm的小正方体搭一搭。
(1)搭一个稍大一些的正方体,至少需要多少个小正方体?
动手试一试。
8个
【教材P20“做一做”】
(2)用12个小正方体搭一个长方体,可以有几种不同的搭
法?记录搭出的长方体的长、宽、高。
(去掉重复数据) 长 宽 高
搭法①
搭法②
搭法③
搭法④
12 cm
1 cm
1 cm
①
②
6 cm
2 cm
1 cm
③
4 cm
3 cm
1 cm
④
3 cm
2 cm
2 cm
【教材P20“做一做”】
1.用棱长1 cm的小正方体搭一搭。
(3)搭一个4个面都是正方形的长方体,你发现了什么?
搭成的长方体实际是一个正方体。
【教材P21 练习五 第4题】
10 cm
10 cm
10 cm
(1)这个魔方是什么形状的?
正方体形状
(2)它的棱长是多少?
10 cm
(3)它有几个面的形状完全相同?
6个
2.
3.一个正方体纸盒每个面的周长都是16 dm,它的棱长总和
是多少分米?
棱长总和:4×12 = 48(dm)
答:它的棱长总和是48分米。
棱长:16÷4 = 4(dm)
4.把2个棱长为2 cm的小正方体拼成一个长方体,这个长方体的棱长总和是多少厘米?
(4+2+2)×4 = 32(厘米)
答:这个长方体的棱长总和是32厘米。
2 cm
2 cm
2 cm
2 cm
长:2+2 = 4(厘米)
5.两根同样长的铁丝,一根正好围成一个长9 cm、宽4 cm、高2 cm的长方体框架,另一根正好围成一个正方体框架,这个正方体的棱长是多少厘米?(接头忽略不计)
分析:先算出这根铁丝的总长度,再计算正方体的棱长。
这根铁丝的总长度 =(9+4+2)×4 = 60(cm)
答:这个正方体的棱长是5厘米。
正方体的棱长为:60÷12 = 5(cm)
你知道吗?
几何学和欧几里得
几何学是数学学科的一个重要分支,它源于土地测量等实际需要。
古希腊数学家欧几里得被称为“几何学之父”,他的著作《原本》在数学发展史上有着深远的影响。
点击输入标题
点此输入内容或者复制您的内容在这里,在此框中选择粘贴,并选择只保留文字。点此输入内容或者复制您的内容在这里,在此框中选择粘贴,并选择只保留文字。
点击此处输入标题
今天我学会了……
课堂总结
正方体的特征 名称 面 棱 顶点
个数 形状 大小关系 条数 长度关系 个数
正方体
6
正方形
完全相同
12
长度相等
8
正方体的棱长总和 = 棱长×12
长方体
正方体
正方体是特殊的长方体
学习态度
学习自信
学习合作
素养评价
1.完成《分层作业》中对应练习。
2.预习下一节内容。
课后作业
课程结束
人教版数学五年级下册
第
三
单
元
2.认识正方体
看图填空。
20 cm
10 cm
10 cm
(1)长方体有_____个面;_____条棱;_____个顶点。
(2)长方体有_____条长;_____条宽;_____条高。
(3)这个长方体的棱长总和是_______。
6
12
8
4
4
4
160 cm
(20+10+10)×4 = 160(cm)
按下面的方法将长方体平均成两份,得到的是什么呢?
你在生活中见过正方体吗?
正方体
正方体也叫立方体。
关于正方体,你知道哪些知识呢?
面
面
面与面相交的线段叫作:棱[léng]
棱与棱的交点叫作:顶点
交流互动:
拿一个正方体的物品来观察,并在小组内说一说你有什么发现?
6
完全相同的正方形
正方体的面
正方体有____个面,它们是_________________。
相对的棱互相______,相邻的棱互相______。
正方体有______条棱,它们_______________。
正方体的棱和顶点
12
长度都相等
平行
垂直
棱
棱
棱
正方体不需要用长、宽、高来区分。
正方体有8个顶点。
同桌合作:剪下本书附页中图2的图样做一个正方体,再量
出它的棱长是多少厘米。
0
1
2
3
4
5
3 cm
3×12 = 36(cm)
你能求出这个正方体的棱长总和吗?
正方体的棱长总和 = 棱长×12
长方体和长方体有哪些相同点?有哪些不同点?填入下表。
长方体 正方体
相同点 不同点
都有___个面、___条棱和___个顶点。
6 个面是长方形(特殊情况两个相对的面是正方形)
相对的面__________。
6 个面都是完全
相同的_______。
相对的棱的长度_____。
12条棱的长度都相等。
完全相同
正方形
相等
6
12
8
你能用集合的方式表示正方体和长方体的关系吗?
长方体
正方体
正方体是长、宽、高都相等的长方体。
【教材P20“做一做”】
1.用棱长1 cm的小正方体搭一搭。
(1)搭一个稍大一些的正方体,至少需要多少个小正方体?
动手试一试。
8个
【教材P20“做一做”】
(2)用12个小正方体搭一个长方体,可以有几种不同的搭
法?记录搭出的长方体的长、宽、高。
(去掉重复数据) 长 宽 高
搭法①
搭法②
搭法③
搭法④
12 cm
1 cm
1 cm
①
②
6 cm
2 cm
1 cm
③
4 cm
3 cm
1 cm
④
3 cm
2 cm
2 cm
【教材P20“做一做”】
1.用棱长1 cm的小正方体搭一搭。
(3)搭一个4个面都是正方形的长方体,你发现了什么?
搭成的长方体实际是一个正方体。
【教材P21 练习五 第4题】
10 cm
10 cm
10 cm
(1)这个魔方是什么形状的?
正方体形状
(2)它的棱长是多少?
10 cm
(3)它有几个面的形状完全相同?
6个
2.
3.一个正方体纸盒每个面的周长都是16 dm,它的棱长总和
是多少分米?
棱长总和:4×12 = 48(dm)
答:它的棱长总和是48分米。
棱长:16÷4 = 4(dm)
4.把2个棱长为2 cm的小正方体拼成一个长方体,这个长方体的棱长总和是多少厘米?
(4+2+2)×4 = 32(厘米)
答:这个长方体的棱长总和是32厘米。
2 cm
2 cm
2 cm
2 cm
长:2+2 = 4(厘米)
5.两根同样长的铁丝,一根正好围成一个长9 cm、宽4 cm、高2 cm的长方体框架,另一根正好围成一个正方体框架,这个正方体的棱长是多少厘米?(接头忽略不计)
分析:先算出这根铁丝的总长度,再计算正方体的棱长。
这根铁丝的总长度 =(9+4+2)×4 = 60(cm)
答:这个正方体的棱长是5厘米。
正方体的棱长为:60÷12 = 5(cm)
你知道吗?
几何学和欧几里得
几何学是数学学科的一个重要分支,它源于土地测量等实际需要。
古希腊数学家欧几里得被称为“几何学之父”,他的著作《原本》在数学发展史上有着深远的影响。
点击输入标题
点此输入内容或者复制您的内容在这里,在此框中选择粘贴,并选择只保留文字。点此输入内容或者复制您的内容在这里,在此框中选择粘贴,并选择只保留文字。
点击此处输入标题
今天我学会了……
课堂总结
正方体的特征 名称 面 棱 顶点
个数 形状 大小关系 条数 长度关系 个数
正方体
6
正方形
完全相同
12
长度相等
8
正方体的棱长总和 = 棱长×12
长方体
正方体
正方体是特殊的长方体
学习态度
学习自信
学习合作
素养评价
1.完成《分层作业》中对应练习。
2.预习下一节内容。
课后作业
课程结束
