2024-2025学年北师大版八年级数学下册课件1.3 线段的垂直平分线课时2 三角形三边的垂直平分线的性质(共31张PPT)
文档属性
| 名称 | 2024-2025学年北师大版八年级数学下册课件1.3 线段的垂直平分线课时2 三角形三边的垂直平分线的性质(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-05 00:00:00 | ||
图片预览










文档简介
(共31张PPT)
北师大版八年级数学下册课件
第一章 三角形的证明
1.3 线段的垂直平分线
课时2 三角形三边的垂直平分线的性质
三角形三边的垂直平分线
线段垂直平分线的作图及应用.(重点、难点)
学习目标
新课导入
线段的垂直平分线的性质与判定的内容是什么?
新课讲解
知识点1 三角形三边的垂直平分线
例
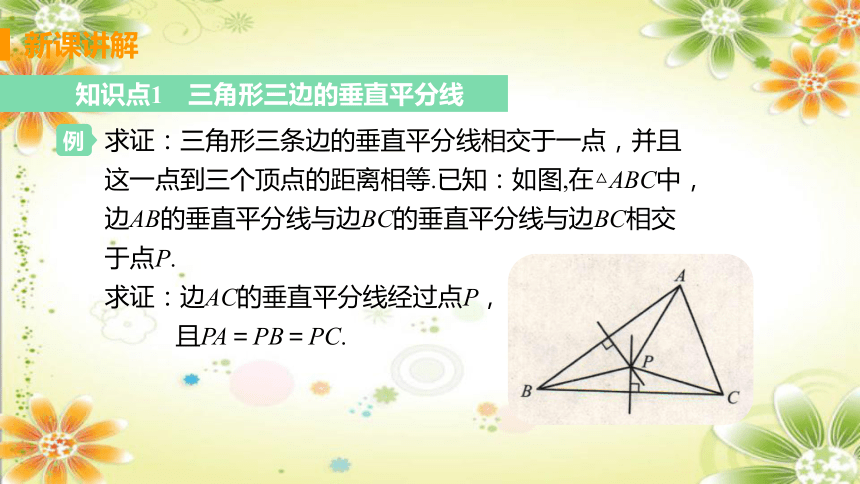
求证:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.已知:如图,在△ABC中,
边AB的垂直平分线与边BC的垂直平分线与边BC相交于点P.
求证:边AC的垂直平分线经过点P,
且PA=PB=PC.
新课讲解
∵点P在线段AB的垂直平分线上,
∴ PA = PB(线段垂直平分线上的点到这条线段
两个端点的距离相等).
同理,PB =PC.
∴点P在线段AC的垂直平分线上(到一条线段
两个端点距离相等的点,在这条线段的垂直
平分线上),
即边AC的垂直平分线经过点P.
证明:
新课讲解
三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
①锐角三角形三边的垂直平分线交于三角形内部
新课讲解
③钝角三角形三边的垂直平分线交于三角形外部
②直角三角形三边的垂直平分线交于三角形斜边中点处
新课讲解
知识点2 线段垂直平分线的作图及应用
议一议
(1)已知三角形的一条边及这条边上的高,你能画出
满足条件的三角形吗?如果能,能画出几个?所
画出的三角形都全等吗?
(2)已知等腰三角形的底边及底边上的高,你能用尺
规作出满足条件的一 个等腰三角形吗?
新课讲解
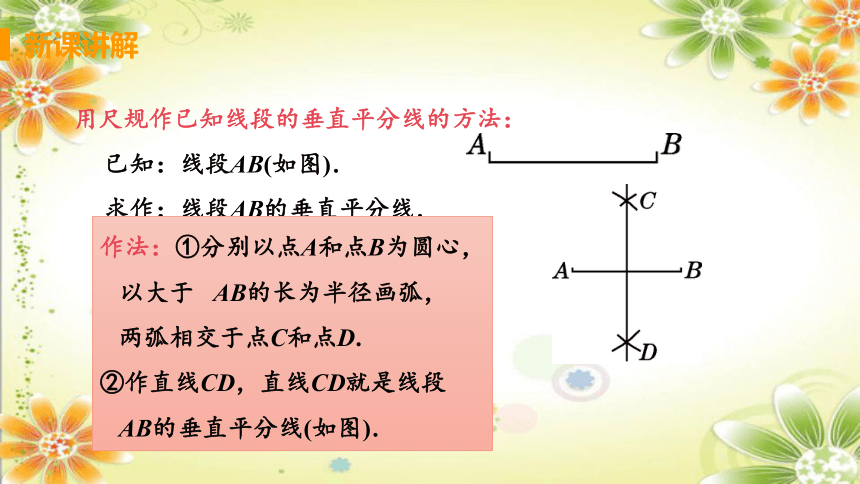
用尺规作已知线段的垂直平分线的方法:
已知:线段AB(如图).
求作:线段AB的垂直平分线.
作法:①分别以点A和点B为圆心,
以大于 AB的长为半径画弧,
两弧相交于点C和点D.
②作直线CD,直线CD就是线段
AB的垂直平分线(如图).
课堂小结
1.三角形三条边的垂直平分线交于同一点,这一点叫
做三角形的外心(三角形外接圆的圆心,以后即可学
到).
2.几种三角形三条边的垂直平分线交点的位置情况:
(1)锐角三角形三边垂直平分线交于三角形内部;
(2)直角三角形三边垂直平分线交于三角形斜边中点;
(3)钝角三角形三边垂直平分线交于三角形外部.
当堂小练
1.如图,在△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC,AD,AB于点E,O,F,则图中全等三角形的对数是( )
A.1对
B.2对
C.3对
D.4对
D
当堂小练
2.已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( )
D
(1)三角形三条边的垂直平分线 ,并且这一点到
的距离 .
(2)如图,若点P是△ABC三边的垂直平分线的交点,
则PA PB PC.
三角形三条边的垂直平分线的性质
三个顶点
相交于一点
相等
=
=
1.(北师8下P24、人教8上P66)如图,在△ABC中,边AB,BC的垂直平分线相交于点P.
(1)求证:PA=PB=PC;
(2)点P是否也在边AC的垂直平分线上?由此你还能得出什么结论?
(1)证明:∵点P是AB的垂直平分线上的点,
∴PA=PB.
同理,PB=PC,∴PA=PB=PC.
(2)解:由(1)得,点P也在边AC的垂直平分线上,
由此可以得出,三角形三条边的垂直平分线相交于一点.
2.(北师8下P25、人教8上P78)已知等腰三角形底边a及底边上的高h,求作等腰三角形.(不写作法,保留作图痕迹)
已知: ;
求作: .
线段a,h
等腰三角形ABC,使CA=CB,AB=a,AB边上的高为h
解:如图,△ABC即为所求作.
(北师8下P25)如图,已知直线l和l上一点P,用尺规作l的垂线,使它经过点P.
过一点作已知直线的垂线(尺规作图)
解:如图,直线PQ即为所求作.
3.(北师8下P26、人教8上P62)如图,已知直线l与直线l外一点P,过点P作出直线l的垂线.
解:如图,直线PQ即为所求作.
4.【例1】(北师8下P26)如图,已知线段a,求作以a为底边、以a为高的等腰三角形,这个等腰三角形有什么特征?
解:如图,△ABC即为所求作.
△ABC是等腰直角三角形.
6.(北师8下P26)尺规作图:如图,已知△ABC,求作:
(1)AC边上的高;(2)BC边上的高.
解:(1)如图,线段BD即为△ABC 的AC边上的高.
(2)如图,线段AK即为△ABC 的BC边上的高.
5.【例2】如图,某公园有摩天轮、海盗船、碰碰车三个娱乐项目,现要在公园内建一个售票中心,使得三个娱乐项目所处位置到售票中心的距离相等,请在图中确定售票中心的位置.
解:如图,①连接AB,AC;
②分别作线段AB,AC的垂直平分线,两垂直平分线相交于点P,则点P即为售票中心的位置.
7.(跨学科融合)如图,一辆汽车在笔直的公路AB上由A向B行驶,M,N分别是位于公路AB两侧的村庄,当汽车行驶到哪个位置时,与村庄M,N的距离相等?请在图中确定这个位置.
解:如图,①连接MN;
②作线段MN的垂直平分线l,交直线AB于点C,则当汽车行驶到点C的位置时,与村庄M,N的距离相等.
★8. (北师8下P27)如图,某市三个城镇中心A,B,C恰好分别位于一个等边三角形的三个顶点处,在三个城镇中心之间铺设通信光缆,以城镇A为出发点设计了两种连接方案:
(1)AD+BC(D为BC的中点);
(2)OA+OB+OC(O为△ABC三边的垂直平分线的交点).
要使铺设的光缆长度最短,应选哪种方案?
0.40
(1) (2)
解:应选方案(2),理由如下:设等边三角形的边长为2a.
如题图(1),∵△ABC是等边三角形,D为BC的中点,
∴AD垂直平分BC,BD=a,
∴AD==a,∴AD+BC=(+2)a.
如题图(2),OA=OB=OC,∠OBD=∠ABC=30°,
∴OB=2OD,
在Rt△OBD中,OB2-a2=,∴OB=a,
∴OA+OB+OC=2a,∴AD+BC>OA+OB+OC.
∴要使铺设的光缆长度最短,应选方案(2).
(1)
(2)
请完成本节课后对应习题
布置作业
感谢大家观看
北师大版八年级数学下册课件
第一章 三角形的证明
1.3 线段的垂直平分线
课时2 三角形三边的垂直平分线的性质
三角形三边的垂直平分线
线段垂直平分线的作图及应用.(重点、难点)
学习目标
新课导入
线段的垂直平分线的性质与判定的内容是什么?
新课讲解
知识点1 三角形三边的垂直平分线
例
求证:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.已知:如图,在△ABC中,
边AB的垂直平分线与边BC的垂直平分线与边BC相交于点P.
求证:边AC的垂直平分线经过点P,
且PA=PB=PC.
新课讲解
∵点P在线段AB的垂直平分线上,
∴ PA = PB(线段垂直平分线上的点到这条线段
两个端点的距离相等).
同理,PB =PC.
∴点P在线段AC的垂直平分线上(到一条线段
两个端点距离相等的点,在这条线段的垂直
平分线上),
即边AC的垂直平分线经过点P.
证明:
新课讲解
三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
①锐角三角形三边的垂直平分线交于三角形内部
新课讲解
③钝角三角形三边的垂直平分线交于三角形外部
②直角三角形三边的垂直平分线交于三角形斜边中点处
新课讲解
知识点2 线段垂直平分线的作图及应用
议一议
(1)已知三角形的一条边及这条边上的高,你能画出
满足条件的三角形吗?如果能,能画出几个?所
画出的三角形都全等吗?
(2)已知等腰三角形的底边及底边上的高,你能用尺
规作出满足条件的一 个等腰三角形吗?
新课讲解
用尺规作已知线段的垂直平分线的方法:
已知:线段AB(如图).
求作:线段AB的垂直平分线.
作法:①分别以点A和点B为圆心,
以大于 AB的长为半径画弧,
两弧相交于点C和点D.
②作直线CD,直线CD就是线段
AB的垂直平分线(如图).
课堂小结
1.三角形三条边的垂直平分线交于同一点,这一点叫
做三角形的外心(三角形外接圆的圆心,以后即可学
到).
2.几种三角形三条边的垂直平分线交点的位置情况:
(1)锐角三角形三边垂直平分线交于三角形内部;
(2)直角三角形三边垂直平分线交于三角形斜边中点;
(3)钝角三角形三边垂直平分线交于三角形外部.
当堂小练
1.如图,在△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC,AD,AB于点E,O,F,则图中全等三角形的对数是( )
A.1对
B.2对
C.3对
D.4对
D
当堂小练
2.已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( )
D
(1)三角形三条边的垂直平分线 ,并且这一点到
的距离 .
(2)如图,若点P是△ABC三边的垂直平分线的交点,
则PA PB PC.
三角形三条边的垂直平分线的性质
三个顶点
相交于一点
相等
=
=
1.(北师8下P24、人教8上P66)如图,在△ABC中,边AB,BC的垂直平分线相交于点P.
(1)求证:PA=PB=PC;
(2)点P是否也在边AC的垂直平分线上?由此你还能得出什么结论?
(1)证明:∵点P是AB的垂直平分线上的点,
∴PA=PB.
同理,PB=PC,∴PA=PB=PC.
(2)解:由(1)得,点P也在边AC的垂直平分线上,
由此可以得出,三角形三条边的垂直平分线相交于一点.
2.(北师8下P25、人教8上P78)已知等腰三角形底边a及底边上的高h,求作等腰三角形.(不写作法,保留作图痕迹)
已知: ;
求作: .
线段a,h
等腰三角形ABC,使CA=CB,AB=a,AB边上的高为h
解:如图,△ABC即为所求作.
(北师8下P25)如图,已知直线l和l上一点P,用尺规作l的垂线,使它经过点P.
过一点作已知直线的垂线(尺规作图)
解:如图,直线PQ即为所求作.
3.(北师8下P26、人教8上P62)如图,已知直线l与直线l外一点P,过点P作出直线l的垂线.
解:如图,直线PQ即为所求作.
4.【例1】(北师8下P26)如图,已知线段a,求作以a为底边、以a为高的等腰三角形,这个等腰三角形有什么特征?
解:如图,△ABC即为所求作.
△ABC是等腰直角三角形.
6.(北师8下P26)尺规作图:如图,已知△ABC,求作:
(1)AC边上的高;(2)BC边上的高.
解:(1)如图,线段BD即为△ABC 的AC边上的高.
(2)如图,线段AK即为△ABC 的BC边上的高.
5.【例2】如图,某公园有摩天轮、海盗船、碰碰车三个娱乐项目,现要在公园内建一个售票中心,使得三个娱乐项目所处位置到售票中心的距离相等,请在图中确定售票中心的位置.
解:如图,①连接AB,AC;
②分别作线段AB,AC的垂直平分线,两垂直平分线相交于点P,则点P即为售票中心的位置.
7.(跨学科融合)如图,一辆汽车在笔直的公路AB上由A向B行驶,M,N分别是位于公路AB两侧的村庄,当汽车行驶到哪个位置时,与村庄M,N的距离相等?请在图中确定这个位置.
解:如图,①连接MN;
②作线段MN的垂直平分线l,交直线AB于点C,则当汽车行驶到点C的位置时,与村庄M,N的距离相等.
★8. (北师8下P27)如图,某市三个城镇中心A,B,C恰好分别位于一个等边三角形的三个顶点处,在三个城镇中心之间铺设通信光缆,以城镇A为出发点设计了两种连接方案:
(1)AD+BC(D为BC的中点);
(2)OA+OB+OC(O为△ABC三边的垂直平分线的交点).
要使铺设的光缆长度最短,应选哪种方案?
0.40
(1) (2)
解:应选方案(2),理由如下:设等边三角形的边长为2a.
如题图(1),∵△ABC是等边三角形,D为BC的中点,
∴AD垂直平分BC,BD=a,
∴AD==a,∴AD+BC=(+2)a.
如题图(2),OA=OB=OC,∠OBD=∠ABC=30°,
∴OB=2OD,
在Rt△OBD中,OB2-a2=,∴OB=a,
∴OA+OB+OC=2a,∴AD+BC>OA+OB+OC.
∴要使铺设的光缆长度最短,应选方案(2).
(1)
(2)
请完成本节课后对应习题
布置作业
感谢大家观看
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
