【备课无忧】人教版五下-3.9 体积单位间的进率(二)(教学设计含反思)
文档属性
| 名称 | 【备课无忧】人教版五下-3.9 体积单位间的进率(二)(教学设计含反思) |
|
|
| 格式 | docx | ||
| 文件大小 | 165.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-05 00:00:00 | ||
图片预览


文档简介
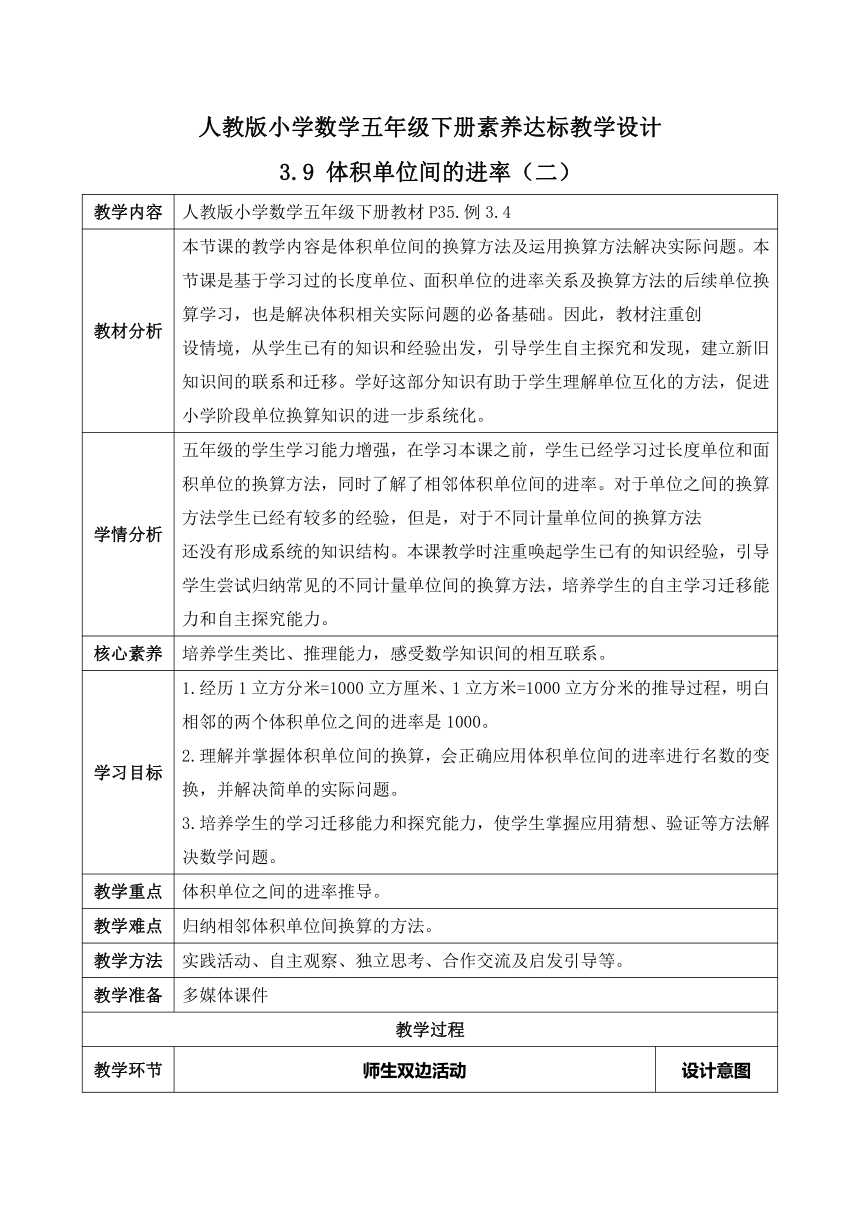
人教版小学数学五年级下册素养达标教学设计
3.9 体积单位间的进率(二)
教学内容 人教版小学数学五年级下册教材P35.例3.4
教材分析 本节课的教学内容是体积单位间的换算方法及运用换算方法解决实际问题。本节课是基于学习过的长度单位、面积单位的进率关系及换算方法的后续单位换算学习,也是解决体积相关实际问题的必备基础。因此,教材注重创 设情境,从学生已有的知识和经验出发,引导学生自主探究和发现,建立新旧知识间的联系和迁移。学好这部分知识有助于学生理解单位互化的方法,促进小学阶段单位换算知识的进一步系统化。
学情分析 五年级的学生学习能力增强,在学习本课之前,学生已经学习过长度单位和面积单位的换算方法,同时了解了相邻体积单位间的进率。对于单位之间的换算方法学生已经有较多的经验,但是,对于不同计量单位间的换算方法 还没有形成系统的知识结构。本课教学时注重唤起学生已有的知识经验,引导学生尝试归纳常见的不同计量单位间的换算方法,培养学生的自主学习迁移能力和自主探究能力。
核心素养 培养学生类比、推理能力,感受数学知识间的相互联系。
学习目标 1.经历1立方分米=1000立方厘米、1立方米=1000立方分米的推导过程,明白相邻的两个体积单位之间的进率是1000。 2.理解并掌握体积单位间的换算,会正确应用体积单位间的进率进行名数的变换,并解决简单的实际问题。 3.培养学生的学习迁移能力和探究能力,使学生掌握应用猜想、验证等方法解决数学问题。
教学重点 体积单位之间的进率推导。
教学难点 归纳相邻体积单位间换算的方法。
教学方法 实践活动、自主观察、独立思考、合作交流及启发引导等。
教学准备 多媒体课件
教学过程
教学环节 师生双边活动 设计意图
一、 知识链接 师:谁来说说体积单位间的进率是多少? 生:1m3=1000 dm3,1dm3=1000 cm3。 师:那这几道题,大家能做出来吗? 出示题目: 在括号里填上合适的数。 4 dm3 =( )cm3 0.8 cm3 =( )dm3 720 dm3 =( )m3 300 cm3 =( )m3 学生举手回答。 师:相邻体积单位间进率是1000。这节课就来继续研究体积单位间的进率。 通过复习旧知,以旧引新,实现旧知识到新知识的顺向迁移,不仅符合学生的认知规律,而且能有效地激励学生积极地探究新知。
二、 探究新知 1.体积单位间的换算① 例3:右面这个牛奶包装箱的体积是多少? (1)理解题意 师:箱上的尺寸“50×30×40”指的是什么呢? 生:这个长方体的长、宽、高分别是50 cm、30 cm、40 cm。 (2)解决问题 师:已知这个长方体的长、宽、高,你们能求出它的体积吗? 学生讨论,汇报结果。 生:50×30×40=60000(cm3)。 师:60000 cm3等于多少60 dm3等于多少0.06 m3? 生:60000 cm3 = 60 dm3 = 0.06 m3。 师:非常好,这个牛奶包装箱的体积是0.06立方米。 2.体积单位间的换算② (1)2 m3 300 dm3 =( )dm3 (2)8.25 dm3 =( )dm3( )cm3 (1)解决问题(1) 师:你们怎么理解2 m3 300 dm3等于多少立方分米呢? 生:先把2 m3换算成以dm3为单位的数,再加300 dm3即可。 师:2 m3等于多少立方分米呢? 生:2 m3 = 2000 dm3。 (2)解决问题(1) 师:第(2)题怎么做呢? 生:8.25 dm3等于8 dm3加0.25 dm3,0.25 dm3=250 cm3。 师:对的,所以8.25 dm3 = 8 dm3 250 cm3。 3.做一做:(教材P35第2题) 要砌一面长15 m、厚24 cm、高3 m的砖墙,如果每立方米用砖525块,至少要用砖多少块? 学生独立完成,全班校对。 通过例4,让学生再次尝试应用相邻单位间的进率进行不同体积单位的换算。通过稍复杂的单位换算的练习,让学生主动参与学习过程,通过计算、自主探索、合作交流等活动,掌握数学知识。
三、 课堂演练 一、选择题。 1.在4.06 m3、406000 cm3、4060 dm3这一组数据中,数据( B )与其他数据不相等。 A.4.06 m3 B.4060000 cm3 C.40060 dm3 2.在5084 dm2、5.084 m2、508400 cm2、50.84 m2这四个数据中,相等的数据有( C )个。 A.0 B.2 C.3 二、单位换算。 7.62 m3=7620 dm3=7620000 cm3 2670 dm3=2 m3670 dm3 4 dm3 33 cm3=4033 dm3 三、一个长方体包装盒,从里面量长28 cm,宽20 cm,里面的体积为11.76 dm3。用它装一件长25 cm、宽16 cm、高18 cm的玻璃器皿,是否装得进去?说一说你的理由。(教材P36第2题) 11.76 dm3= 11760 cm3 11760÷28÷20 = 21(cm) 28 > 25 20 > 16 21 > 18 答:可以装得下。 四、“六一”儿童节前,小学生用棱长3 cm的正方体塑料拼插积木在广场中央搭起了一面长6 m、宽2.7 m、厚6 cm的心愿墙。这面墙一共用了多少块积木?(教材P36第4题) 6 m = 600 cm 2.7 m = 270 cm 奥运心愿墙的体积:600×270×6 = 972000(cm3) 积木的体积:3×3×3 = 27(cm3) 972000÷27 = 36000(块) 答:这面墙一共用了36000块积木。 主要是巩固课堂所学的知识,提升解决问题的能力。
四、 总结评价 1.课堂总结 2.素养评价 3.布置作业 (1)完成《分层作业》中对应练习。 (2)预习下一节内容。
板书设计
课后作业 1.完成《分层作业》中对应练习; 2.预习下一节内容。
课后反思 通过本节课的练习,发现同学们对面积单位、体积单位的换算都掌握得比较好。但在具体问题具体分析这块,还有待加强。特别是第9题,对学生有一定的挑战,教学时可引导学生先讨论解决这类问题的方法,引导学生思考,建立如何摆放的表象。针对有困难的学生,可用课件帮助学生理解,从而突破难点。由于没有教具让学生实际动手操作,学生理解起来还是有难度,要加强学生几何直观的培养。
3.9 体积单位间的进率(二)
教学内容 人教版小学数学五年级下册教材P35.例3.4
教材分析 本节课的教学内容是体积单位间的换算方法及运用换算方法解决实际问题。本节课是基于学习过的长度单位、面积单位的进率关系及换算方法的后续单位换算学习,也是解决体积相关实际问题的必备基础。因此,教材注重创 设情境,从学生已有的知识和经验出发,引导学生自主探究和发现,建立新旧知识间的联系和迁移。学好这部分知识有助于学生理解单位互化的方法,促进小学阶段单位换算知识的进一步系统化。
学情分析 五年级的学生学习能力增强,在学习本课之前,学生已经学习过长度单位和面积单位的换算方法,同时了解了相邻体积单位间的进率。对于单位之间的换算方法学生已经有较多的经验,但是,对于不同计量单位间的换算方法 还没有形成系统的知识结构。本课教学时注重唤起学生已有的知识经验,引导学生尝试归纳常见的不同计量单位间的换算方法,培养学生的自主学习迁移能力和自主探究能力。
核心素养 培养学生类比、推理能力,感受数学知识间的相互联系。
学习目标 1.经历1立方分米=1000立方厘米、1立方米=1000立方分米的推导过程,明白相邻的两个体积单位之间的进率是1000。 2.理解并掌握体积单位间的换算,会正确应用体积单位间的进率进行名数的变换,并解决简单的实际问题。 3.培养学生的学习迁移能力和探究能力,使学生掌握应用猜想、验证等方法解决数学问题。
教学重点 体积单位之间的进率推导。
教学难点 归纳相邻体积单位间换算的方法。
教学方法 实践活动、自主观察、独立思考、合作交流及启发引导等。
教学准备 多媒体课件
教学过程
教学环节 师生双边活动 设计意图
一、 知识链接 师:谁来说说体积单位间的进率是多少? 生:1m3=1000 dm3,1dm3=1000 cm3。 师:那这几道题,大家能做出来吗? 出示题目: 在括号里填上合适的数。 4 dm3 =( )cm3 0.8 cm3 =( )dm3 720 dm3 =( )m3 300 cm3 =( )m3 学生举手回答。 师:相邻体积单位间进率是1000。这节课就来继续研究体积单位间的进率。 通过复习旧知,以旧引新,实现旧知识到新知识的顺向迁移,不仅符合学生的认知规律,而且能有效地激励学生积极地探究新知。
二、 探究新知 1.体积单位间的换算① 例3:右面这个牛奶包装箱的体积是多少? (1)理解题意 师:箱上的尺寸“50×30×40”指的是什么呢? 生:这个长方体的长、宽、高分别是50 cm、30 cm、40 cm。 (2)解决问题 师:已知这个长方体的长、宽、高,你们能求出它的体积吗? 学生讨论,汇报结果。 生:50×30×40=60000(cm3)。 师:60000 cm3等于多少60 dm3等于多少0.06 m3? 生:60000 cm3 = 60 dm3 = 0.06 m3。 师:非常好,这个牛奶包装箱的体积是0.06立方米。 2.体积单位间的换算② (1)2 m3 300 dm3 =( )dm3 (2)8.25 dm3 =( )dm3( )cm3 (1)解决问题(1) 师:你们怎么理解2 m3 300 dm3等于多少立方分米呢? 生:先把2 m3换算成以dm3为单位的数,再加300 dm3即可。 师:2 m3等于多少立方分米呢? 生:2 m3 = 2000 dm3。 (2)解决问题(1) 师:第(2)题怎么做呢? 生:8.25 dm3等于8 dm3加0.25 dm3,0.25 dm3=250 cm3。 师:对的,所以8.25 dm3 = 8 dm3 250 cm3。 3.做一做:(教材P35第2题) 要砌一面长15 m、厚24 cm、高3 m的砖墙,如果每立方米用砖525块,至少要用砖多少块? 学生独立完成,全班校对。 通过例4,让学生再次尝试应用相邻单位间的进率进行不同体积单位的换算。通过稍复杂的单位换算的练习,让学生主动参与学习过程,通过计算、自主探索、合作交流等活动,掌握数学知识。
三、 课堂演练 一、选择题。 1.在4.06 m3、406000 cm3、4060 dm3这一组数据中,数据( B )与其他数据不相等。 A.4.06 m3 B.4060000 cm3 C.40060 dm3 2.在5084 dm2、5.084 m2、508400 cm2、50.84 m2这四个数据中,相等的数据有( C )个。 A.0 B.2 C.3 二、单位换算。 7.62 m3=7620 dm3=7620000 cm3 2670 dm3=2 m3670 dm3 4 dm3 33 cm3=4033 dm3 三、一个长方体包装盒,从里面量长28 cm,宽20 cm,里面的体积为11.76 dm3。用它装一件长25 cm、宽16 cm、高18 cm的玻璃器皿,是否装得进去?说一说你的理由。(教材P36第2题) 11.76 dm3= 11760 cm3 11760÷28÷20 = 21(cm) 28 > 25 20 > 16 21 > 18 答:可以装得下。 四、“六一”儿童节前,小学生用棱长3 cm的正方体塑料拼插积木在广场中央搭起了一面长6 m、宽2.7 m、厚6 cm的心愿墙。这面墙一共用了多少块积木?(教材P36第4题) 6 m = 600 cm 2.7 m = 270 cm 奥运心愿墙的体积:600×270×6 = 972000(cm3) 积木的体积:3×3×3 = 27(cm3) 972000÷27 = 36000(块) 答:这面墙一共用了36000块积木。 主要是巩固课堂所学的知识,提升解决问题的能力。
四、 总结评价 1.课堂总结 2.素养评价 3.布置作业 (1)完成《分层作业》中对应练习。 (2)预习下一节内容。
板书设计
课后作业 1.完成《分层作业》中对应练习; 2.预习下一节内容。
课后反思 通过本节课的练习,发现同学们对面积单位、体积单位的换算都掌握得比较好。但在具体问题具体分析这块,还有待加强。特别是第9题,对学生有一定的挑战,教学时可引导学生先讨论解决这类问题的方法,引导学生思考,建立如何摆放的表象。针对有困难的学生,可用课件帮助学生理解,从而突破难点。由于没有教具让学生实际动手操作,学生理解起来还是有难度,要加强学生几何直观的培养。
