2024-2025学年北师大版八年级数学下册课件1.4 角平分线课时2 三角形三个内角的平分线的性质(共31张PPT)
文档属性
| 名称 | 2024-2025学年北师大版八年级数学下册课件1.4 角平分线课时2 三角形三个内角的平分线的性质(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 880.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-05 11:58:56 | ||
图片预览











文档简介
(共31张PPT)
北师大版八年级数学下册课件
第一章 三角形的证明
1.4 角平分线
课时2 三角形三个内角的平分线的性质
三角形的角平分线
三角形的角平分线的应用.(重点、难点)
学习目标
新课导入
角平分线的性质与判定的内容是什么?
新课讲解
知识点1 三角形的角平分线
例
求证:三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等.
新课讲解
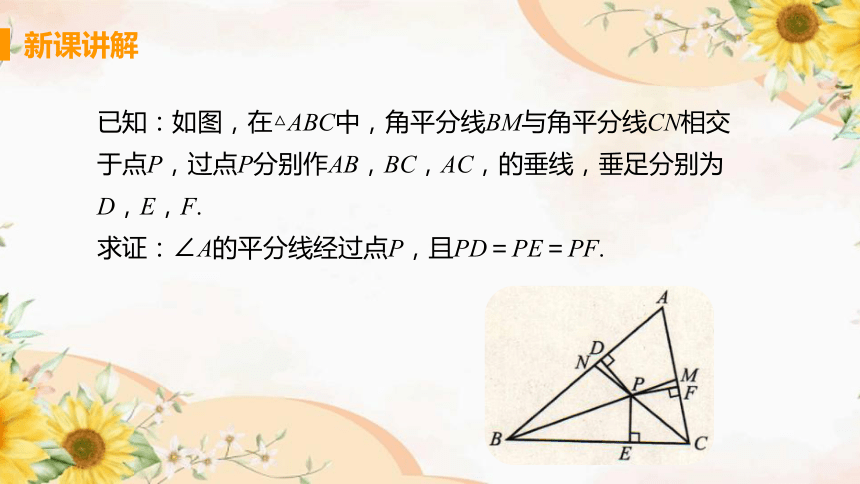
已知:如图,在△ABC中,角平分线BM与角平分线CN相交于点P,过点P分别作AB,BC,AC,的垂线,垂足分别为D,E,F.
求证:∠A的平分线经过点P,且PD=PE=PF.
新课讲解
∵BM是△ABC的角平分线,点P在BM上,且
PD丄AB,PE丄BC,垂足分别为D,E,
∴PD=PE (角平分线上的点到这个角的两边的
距离相等).
同理,PE=PF.
∴PD=PE=PF.
∴点P在∠A的平分线上(在一个角的内部,到
角的两边距离相等的点在这个角的平分线上),
即 ∠A的平分线经过点P.
证明:
新课讲解
三角形的三条角平分线相交于一点,并且这一点到三角形三条边的距离相等.
新课讲解
知识点2 三角形的角平分线的应用
角平分线的性质是证明边相等的重要依据,常
与直角三角形的性质、勾股定理其逆定理等综合应
用,在应用中常用到“构造法”和“转化思想”.
课堂小结
三角形三条内角平分线的交点到三边的距离相等是三角形的一个重要特征,该交点与三角形三个顶点的连线形成三个等高的小三角形,利用三个小三角形的面积之和等于原三角形的面积,求角平分线交点到三边距离或者求三角形的面积,体现等面积法的运用.
当堂小练
1.到三角形三边距离相等的点的个数是( )
A.1 B.2
C.3 D.4
D
当堂小练
2 如图,李明计划在张村、李村之间建一家超市.张、李两村坐落在两相交公路内.超市的位置应满足下列条件:(1)使其到两公路的距离相等;(2)为了方便群众,超市到两村的距离之和最短,请你通过作图确定要建超市的位置.
如图,连接EF,作∠ACB的平分线交EF于点O,则点O就是所要建超市的位置.
解:
拓展与延伸
如图,△ABC的三边AB,BC,CA的长分别为
40,50,60,其三条角平分线交于点O,则S△ABO∶S△BCO∶S△CAO=_______.
4:5:6
性质:三角形的三条角平分线 ,并且这一点到
的距离 .
几何语言:
如图,在△ABC中,角平分线BD,CE相交于点P,过点P作PM⊥BC,PN⊥AC,PF⊥AB,垂足分别为点M,N,F,则PM PN PF.
三角形三个内角的平分线的性质
=
相交于一点
三条边
相等
=
1.(北师8下P30、人教8上P50)如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,OD⊥AB于D,OE⊥AC于E,OF⊥BC于F.求证:∠A的平分线经过点O,且OD=OE=OF.
证明:∵O为∠ABC,∠ACB的平分线的交点,
且OD⊥AB,OE⊥AC,OF⊥BC,
∴OD=OF,OF=OE.∴OD=OE.
∴点O在∠A的平分线上,
∴∠A的平分线经过点O,且OD=OE=OF.
(1)(人教8上P56)如图1,在△ABC中,AD是它的角平分线,则S△ABD∶S△ACD=AB∶AC.
(2)如图2,当点E在角平分线AD上的任何位置(不与点A重合),都有S△ABE∶S△ACE=AB∶AC.
与角平分线有关的面积问题(拓展)
2.(1)如图,AD是△ABC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC的长是 ;
(2)(2024汕头一模)如图,在△ABC中,AD是∠BAC的平分线,AB=8 cm,AC=6 cm,则S△ABD∶S△ACD= .
第(1)题图
第(2)题图
3
4∶3
(1)向角的某边作垂线,构造直角三角形,如图1.
(2)以角平分线为对称轴,构造全等三角形,如图2.
(3)延长角平分线的垂线,构造等腰三角形,如图3.
(4)添加平行线,构造等腰三角形,如图4.
与角平分线有关的常见的添加辅助线的4种方法(拓展)
图1
图2
图3
图4
3.如图,∠AOP=∠BOP=15°,PC∥OB交OA于C,PD⊥OB于D,若PD=2,求PC的长.
解:如图,过点P作PE⊥AO于E,
∵∠AOP=∠BOP=15°,
∴OP是∠AOB的平分线.
∵PD⊥OB,∴PE=PD=2.
∵PC∥OB,∠AOB=15°+15°=30°,
∴∠ECP=∠AOB=30°.
在Rt△ECP中,PC=2PE=2×2=4.
答案图
4.【例1】如图,O是△ABC内一点,且O到三边AB,BC,CA的距离满足OF=OD=OE,若∠BAC=80°,则∠BOC= .
130°
5.【例2】如图,在Rt△ABC中,∠A=90°,BD是∠ABC的平分线,DE是BC的垂直平分线.
求证:BC=2AB.
证明:∵DE是BC的垂直平分线,
∴BE=EC,DE⊥BC.
∵∠A=90°,∴DA⊥AB.
∵BD是∠ABC的平分线,∴DA=DE.
∵BD=BD,∴Rt△ABD≌Rt△EBD.∴AB=BE.
∵BC=2BE,∴BC=2AB.
6.【例3】如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于点E,F在AC上,BD=DF.
(1)求证:CF=EB;
(2)求证:AB=AF+2EB.
证明:(1)∵AD是∠BAC的平分线,DE⊥AB,∠C=90°,∴DE=DC.
在Rt△DCF和Rt△DEB中,
∴Rt△DCF≌Rt△DEB(HL).∴CF=EB.
(2)在Rt△ADC和Rt△ADE中,
∴Rt△ADC≌Rt△ADE(HL).∴AC=AE.
∴AB=AE+EB=AC+EB=AF+CF+EB=AF+2EB.
7.【例4】(跨学科融合)如图是“一带一路”示意图,若记北京为A地,莫斯科为B地,雅典为C地,分别连接AB,AC,BC,形成一个三角形.若想在三角形内建立一个货物中转仓,使其到AB,BC,CA的距离相等,则中转仓的位置应选在 .
∠A,∠B的平分线的交点处(答案不唯一)
8.(2024西安模拟)如图,已知△ABC的周长是20,BO,CO分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,则△ABC的面积是
.
30
9.如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作一直线交AB,AC于E,F,且BE=EO.求证:OF=CF.
证明:∵BE=EO,∴∠EBO=∠EOB.
∵△ABC中,∠ABC与∠ACB的平分线交于点O,
∴∠EBO=∠OBC,∠OCB=∠OCF.∴∠EOB=∠OBC.
∴EF∥BC.∴∠FOC=∠OCB=∠OCF.∴OF=CF.
10.(2024武威模拟)如图,DE⊥AB于点E,DF⊥AC于点F,BD=CD,BE=CF.
(1)求证:AD平分∠BAC;
(2)直接写出AB+AC与AE之间的等量关系.
(1)证明:∵DE⊥AB于点E,DF⊥AC于点F,
∴∠E=∠DFC=90°.
∴△BDE与△CDF均为直角三角形.
∵∴Rt△BDE≌Rt△CDF(HL).
∴DE=DF,∴AD平分∠BAC.
(2)解:AB+AC=2AE.【提示:利用全等分别找出AB,AC与AE的关系】
★11. (北师8下P32、人教8上P55)如图,三条公路两两相交,现计划修建一个油库,要求油库到这三条公路的距离都相等,则满足条件的油库位置有( )
A.1个 B.2个
C.3个 D.4个
0.45
D
请完成本节课后对应习题
布置作业
谢谢观看
北师大版八年级数学下册课件
第一章 三角形的证明
1.4 角平分线
课时2 三角形三个内角的平分线的性质
三角形的角平分线
三角形的角平分线的应用.(重点、难点)
学习目标
新课导入
角平分线的性质与判定的内容是什么?
新课讲解
知识点1 三角形的角平分线
例
求证:三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等.
新课讲解
已知:如图,在△ABC中,角平分线BM与角平分线CN相交于点P,过点P分别作AB,BC,AC,的垂线,垂足分别为D,E,F.
求证:∠A的平分线经过点P,且PD=PE=PF.
新课讲解
∵BM是△ABC的角平分线,点P在BM上,且
PD丄AB,PE丄BC,垂足分别为D,E,
∴PD=PE (角平分线上的点到这个角的两边的
距离相等).
同理,PE=PF.
∴PD=PE=PF.
∴点P在∠A的平分线上(在一个角的内部,到
角的两边距离相等的点在这个角的平分线上),
即 ∠A的平分线经过点P.
证明:
新课讲解
三角形的三条角平分线相交于一点,并且这一点到三角形三条边的距离相等.
新课讲解
知识点2 三角形的角平分线的应用
角平分线的性质是证明边相等的重要依据,常
与直角三角形的性质、勾股定理其逆定理等综合应
用,在应用中常用到“构造法”和“转化思想”.
课堂小结
三角形三条内角平分线的交点到三边的距离相等是三角形的一个重要特征,该交点与三角形三个顶点的连线形成三个等高的小三角形,利用三个小三角形的面积之和等于原三角形的面积,求角平分线交点到三边距离或者求三角形的面积,体现等面积法的运用.
当堂小练
1.到三角形三边距离相等的点的个数是( )
A.1 B.2
C.3 D.4
D
当堂小练
2 如图,李明计划在张村、李村之间建一家超市.张、李两村坐落在两相交公路内.超市的位置应满足下列条件:(1)使其到两公路的距离相等;(2)为了方便群众,超市到两村的距离之和最短,请你通过作图确定要建超市的位置.
如图,连接EF,作∠ACB的平分线交EF于点O,则点O就是所要建超市的位置.
解:
拓展与延伸
如图,△ABC的三边AB,BC,CA的长分别为
40,50,60,其三条角平分线交于点O,则S△ABO∶S△BCO∶S△CAO=_______.
4:5:6
性质:三角形的三条角平分线 ,并且这一点到
的距离 .
几何语言:
如图,在△ABC中,角平分线BD,CE相交于点P,过点P作PM⊥BC,PN⊥AC,PF⊥AB,垂足分别为点M,N,F,则PM PN PF.
三角形三个内角的平分线的性质
=
相交于一点
三条边
相等
=
1.(北师8下P30、人教8上P50)如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,OD⊥AB于D,OE⊥AC于E,OF⊥BC于F.求证:∠A的平分线经过点O,且OD=OE=OF.
证明:∵O为∠ABC,∠ACB的平分线的交点,
且OD⊥AB,OE⊥AC,OF⊥BC,
∴OD=OF,OF=OE.∴OD=OE.
∴点O在∠A的平分线上,
∴∠A的平分线经过点O,且OD=OE=OF.
(1)(人教8上P56)如图1,在△ABC中,AD是它的角平分线,则S△ABD∶S△ACD=AB∶AC.
(2)如图2,当点E在角平分线AD上的任何位置(不与点A重合),都有S△ABE∶S△ACE=AB∶AC.
与角平分线有关的面积问题(拓展)
2.(1)如图,AD是△ABC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC的长是 ;
(2)(2024汕头一模)如图,在△ABC中,AD是∠BAC的平分线,AB=8 cm,AC=6 cm,则S△ABD∶S△ACD= .
第(1)题图
第(2)题图
3
4∶3
(1)向角的某边作垂线,构造直角三角形,如图1.
(2)以角平分线为对称轴,构造全等三角形,如图2.
(3)延长角平分线的垂线,构造等腰三角形,如图3.
(4)添加平行线,构造等腰三角形,如图4.
与角平分线有关的常见的添加辅助线的4种方法(拓展)
图1
图2
图3
图4
3.如图,∠AOP=∠BOP=15°,PC∥OB交OA于C,PD⊥OB于D,若PD=2,求PC的长.
解:如图,过点P作PE⊥AO于E,
∵∠AOP=∠BOP=15°,
∴OP是∠AOB的平分线.
∵PD⊥OB,∴PE=PD=2.
∵PC∥OB,∠AOB=15°+15°=30°,
∴∠ECP=∠AOB=30°.
在Rt△ECP中,PC=2PE=2×2=4.
答案图
4.【例1】如图,O是△ABC内一点,且O到三边AB,BC,CA的距离满足OF=OD=OE,若∠BAC=80°,则∠BOC= .
130°
5.【例2】如图,在Rt△ABC中,∠A=90°,BD是∠ABC的平分线,DE是BC的垂直平分线.
求证:BC=2AB.
证明:∵DE是BC的垂直平分线,
∴BE=EC,DE⊥BC.
∵∠A=90°,∴DA⊥AB.
∵BD是∠ABC的平分线,∴DA=DE.
∵BD=BD,∴Rt△ABD≌Rt△EBD.∴AB=BE.
∵BC=2BE,∴BC=2AB.
6.【例3】如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于点E,F在AC上,BD=DF.
(1)求证:CF=EB;
(2)求证:AB=AF+2EB.
证明:(1)∵AD是∠BAC的平分线,DE⊥AB,∠C=90°,∴DE=DC.
在Rt△DCF和Rt△DEB中,
∴Rt△DCF≌Rt△DEB(HL).∴CF=EB.
(2)在Rt△ADC和Rt△ADE中,
∴Rt△ADC≌Rt△ADE(HL).∴AC=AE.
∴AB=AE+EB=AC+EB=AF+CF+EB=AF+2EB.
7.【例4】(跨学科融合)如图是“一带一路”示意图,若记北京为A地,莫斯科为B地,雅典为C地,分别连接AB,AC,BC,形成一个三角形.若想在三角形内建立一个货物中转仓,使其到AB,BC,CA的距离相等,则中转仓的位置应选在 .
∠A,∠B的平分线的交点处(答案不唯一)
8.(2024西安模拟)如图,已知△ABC的周长是20,BO,CO分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,则△ABC的面积是
.
30
9.如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作一直线交AB,AC于E,F,且BE=EO.求证:OF=CF.
证明:∵BE=EO,∴∠EBO=∠EOB.
∵△ABC中,∠ABC与∠ACB的平分线交于点O,
∴∠EBO=∠OBC,∠OCB=∠OCF.∴∠EOB=∠OBC.
∴EF∥BC.∴∠FOC=∠OCB=∠OCF.∴OF=CF.
10.(2024武威模拟)如图,DE⊥AB于点E,DF⊥AC于点F,BD=CD,BE=CF.
(1)求证:AD平分∠BAC;
(2)直接写出AB+AC与AE之间的等量关系.
(1)证明:∵DE⊥AB于点E,DF⊥AC于点F,
∴∠E=∠DFC=90°.
∴△BDE与△CDF均为直角三角形.
∵∴Rt△BDE≌Rt△CDF(HL).
∴DE=DF,∴AD平分∠BAC.
(2)解:AB+AC=2AE.【提示:利用全等分别找出AB,AC与AE的关系】
★11. (北师8下P32、人教8上P55)如图,三条公路两两相交,现计划修建一个油库,要求油库到这三条公路的距离都相等,则满足条件的油库位置有( )
A.1个 B.2个
C.3个 D.4个
0.45
D
请完成本节课后对应习题
布置作业
谢谢观看
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
