3.2 长方体和正方体的表面积课件(共18张PPT)2024-2025学年五年级下册数学人教版
文档属性
| 名称 | 3.2 长方体和正方体的表面积课件(共18张PPT)2024-2025学年五年级下册数学人教版 |  | |
| 格式 | pptx | ||
| 文件大小 | 815.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-05 13:48:03 | ||
图片预览





文档简介
(共18张PPT)
第三单元 长方体和正方体
3.2 长方体和正方体的表面积
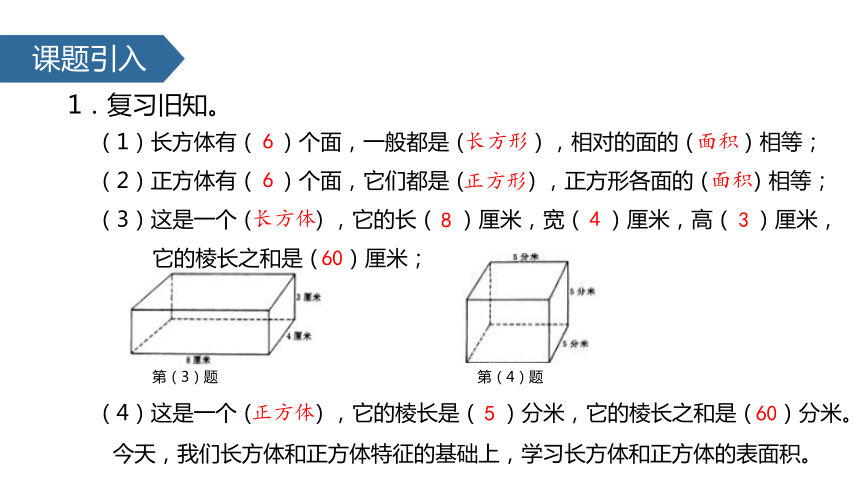
1.复习旧知。
课题引入
6
(1)长方体有( )个面,一般都是( ),相对的面的( )相等;
(2)正方体有( )个面,它们都是( ),正方形各面的( )相等;
(3)这是一个( ),它的长( )厘米,宽( )厘米,高( )厘米,
它的棱长之和是( )厘米;
第(3)题 第(4)题
(4)这是一个( ),它的棱长是( )分米,它的棱长之和是( )分米。
长方形
面积
6
正方形
面积
长方体
8
4
60
3
正方体
5
60
今天,我们长方体和正方体特征的基础上,学习长方体和正方体的表面积。
教学新知
例1:请大家想一下,做一只这样的纸盒要用多少平方厘米的硬纸板?
说说估计的方法。
【答案】(1)20×2+10×2+8×2=76(c㎡),上下两个面的面积,前后两个面的面积,左右两个面的面积,加起来就是六个面的总面积。(2)(20+10+8)×2=76(c㎡)上面、前面和左面三个面的面积的和,再乘2。(3)20+20+10+10+8+8=76(c㎡),把六个面的面积加起来。
【结论】根据长方体有6个面,相对的面的面积相等,从而求出长方体六个面的面积的和。
教学新知
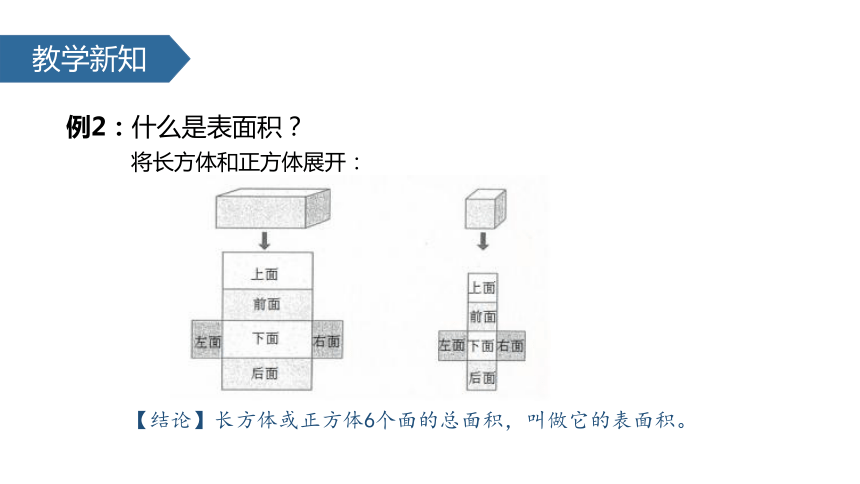
例2:什么是表面积?
将长方体和正方体展开:
【结论】长方体或正方体6个面的总面积,叫做它的表面积。
教学新知
例3:做一个微波炉的包装箱(如下图),至少要用多少平方米的
硬纸板?
上、下每个面,长 ,宽 ,面积是 ;
前、后每个面,长 ,宽 ,面积是 ;
左、右每个面,长 ,宽 ,面积是 。
0.7m
0.5m
0.35㎡
0.7m
0.4m
0.28㎡
0.5m
0.4m
0.2㎡
教学新知
【答案】(1)先用0.7×0.5求出上面的面积,再乘2,求出上下两个面的面积;用0.7×0.4求出前面的面积,再乘2,求出前后两个面的面积;用0.5×0.4求出左面的面积,再乘2,求出左右两个面的面积;再把乘得的积相加。
0.7×0.5×2+0.7×0.4×2+0.5×0.4×2
=0.7+0.56+0.4
=1.66(㎡)
(2)先求出上面、前面和左面三个面的面积的和,再乘2。
(0.7×0.5+0.7×0.4+0.5×0.4)×2
=(0.35+0.28+0.2)×2
=0.83×2
=1.66(㎡)
教学新知
【补充】大家恐怕都知道,长方体表面积是“长×宽×2+宽×高×2+长×高×2”,正方体表面积是“棱长×棱长×6”。但是在生活中可不能就这样生搬硬套,因为书上告诉你的是一般情况,生活中不是这样,有时,可能不用六个面全算。比如,让你给教室刷漆,人们常识性的只会刷上、左右、前后五个面,而你把公式套上去后,就可能连地面也给刷了,这个要注意。下面还有一个实例。
健身中心新建一个游泳池,该游泳池的长50m,宽20m,深2.5m(也就是公式中所说的高),现在让你贴上瓷砖,需要多少瓷砖?
首先,咱们得分析这道题,当然,最好的方法是联系生活实际,展开想象。既然是游泳池,肯定要求底面积,那就用长×宽求得底面积,大家可能会奇怪,为什么不铺上面呢?因为上面是水,铺上的话就不叫游泳池了。四周肯定也要铺,用宽×高×2+长×高×2就得出需要铺多少平方米的地砖了。
所以,其最终结果是1625平方米的地砖。还要注意地砖和游泳池面积的平方米是否一致,不一致还要换算单位。所以说,在解决实际问题时,正方体和长方体的表面积公式只是“半成品”,其中的很多情况是需要你仔细思考的。
资料补充:生活中的长方体和正方体
知识要点
长方体或正方体6个面的总面积,叫做它的表面积。
计算方法:
0.7×0.5 +0.7×0.5+0.5×0.4+0.5×0.4+0.7×0.4+0.7×0.4
0.7×0.5×2+0.5×0.4×2+0.7×0.4×2
(0.7×0.5 +0.5×0.4+0.7×0.4)×2
知识点1:长方体或正方体6个面的总面积,叫做它的表面积。
知识梳理
例 1:一个长方体的形状如图(单位:米):
(1)它的上下两个面的面积=( )×( )×( )。
(2)它的前后两个面的面积=( )×( )×( )。
(3)它的左右两个面的面积=( )×( )×( )。
(4)这个长方体的表面积是( )平方米。
348
15 4 2
15 6 2
4 6 2
知识梳理
小练习:
1.一个长方体的长是6分米,宽1.5分米,高3分米,它的
表面积是( )平方分米。
2.一个正方体的棱长是0.5分米,它的表面积是( )平方分米。
3.一个长4分米、宽2分米、高2分米的长方体,它占地面积最
大是多少?表面积又是多少?
63
1.5
【答案】占地面积最大是4×2=8平方分米;
表面积是(4×2+4×2+2×2)×2=40平方分米。
1.长方体或正方体( )个面的总面积,叫做它们的表面积。
2.计算正方体的表面积可以用( )的方法计算。这是因
为正方体有( )个面,每个面都是( )形,而且( )都相等。
3.一个正方体的表面积是36平方厘米,把它放在桌子上占的面积是( )平方厘米。
4.一个长方体长5厘米,宽5厘米,高4厘米,这个长方体有2个面是( )形,有( )个面的面积相等,长方体的表面积是( )。
课堂练习
6
棱长×棱长×6
6
正方
面积
6
正方
4
130平方厘米
5.做一个不带盖的长方体铁盒,长0.6米,宽0.35米,高0,4米。
至少需要多少平方米铁皮?
课堂练习
【解析】长方体的表面积是长方体6个面的总面积。题目中给出的是做一个不带盖的长方体铁盒,由此可以知道这个长方体铁盒只有5个面,没有上面。根据长方体表面积的计算方法,做这个铁盒至少需要0.6×0.35+(0.6×0.4+0.35×0.4)×2=0.97平方米铁皮。
【答案】0.6×0.35+(0.6×0.4+0.35×0.4)×2=0.97平方米
答:至少需要0.97平方米铁皮。
6.把一个正方体锯成两个长方体,它的表面积增加了6平方厘米,
那么原正方体的表面积是多少平方厘米?
课堂练习
【解析】把一个正方体锯成两个长方体,它增加的表面积也就是这个正方体一个面的面积的2倍,所以其中一个面的面积为6÷2=3平方厘米,而正方体的表面积为6个面面积的总和,也就是其中一个正方形的面积×6,即3×6=18平方厘米。
【答案】8平方厘米。
1.填空。
课后习题
(1)一个长方体正好分割成3个体积相等的正方体。已知一个正方体的
表面积是3平方厘米,原长方体的表面积是( )平方厘米。
(2)把一个长、宽、高分别是5厘米、4厘米、3厘米的长方体截成两个
小长方体,表面积最多增加( )平方厘米、
(3)把六个棱长为3厘米的正方体拼成一个长方体,表面积最多减少( )
平方厘米。
(4)一个长方体木块的表面积是60平方厘米,现在正好把它锯成两个相等
的正方体。每个正方体的表面积是( )平方厘米。
7
40
90
36
课后习题
2.判断。
(1)若一个长方体和一个正方体的所有棱长之和相等,那么他们的表面积
也一定相等。 ( )
(2)一个正方体表面积是18平方厘米,把它切成2个完全相等的长方体,表
面积比原来增加了3平方厘米。 ( )
(3)把两块棱长都是2厘米的正方体拼成一个长方体,表面积减少了8平方
厘米。 ( )
(4)一根长方体木料,横截面是24平方厘米,把它锯成3段后,表面积增加
72平方厘米。 ( )
×
√
×
×
课后习题
3.一个长4米、宽3米、高2米的长方体,它占地面积最大是多少平
方米?表面积是多少平方米?
【答案】面积:4×3=12(平方米)
表面积:(4×3+4×2+3×2)×2=52(平方米)
4.有一种无盖的玻璃鱼缸,长20厘米,宽15厘米,高10厘米,做
这样一对鱼缸需要多少平方厘米的玻璃?
【答案】(20×15+20×10+15×10)×2=1300(平方厘米)
课后习题
5.用72分米长的铁丝做一个正方体的框架,然后在外面贴上一层纸,
至少需要多少平方分米的纸?
【答案】72÷12=6分米,6×6×6=216平方分米
【解析】用72分米长的铁丝做一个正方体的框架,由于正方体有12条棱,且每条棱的长度都相等,因此可以算出这个正方体框架的棱长为72÷12=6分米。现在在这个框架外面贴一层纸,要算纸的面积也就是算这个正方体的表面积,所以一共需要6×6×6=216平方分米的纸。
课后习题
6.发散思维。
【解析】应先算出这个游泳池的表面积和一块瓷砖的面积,而游泳池没有上面,因此可算出游泳池的表面积为25×10+(25×2.4+10×2.4)×2=418(平方米),418平方米=41800平方分米,一块正方形瓷砖的面积为2×2=4(平方分米),因此至少需要这种瓷砖41800÷4=10450块。
一个游泳池,长25米,宽10米,深2.4米,在游泳池的四周和池底砌瓷砖,
如果瓷砖的边长是2分米的正方形,那么至少需要这种瓷砖多少块?
【答案】25×10+(25×2.4+10×2.4)×2=418(平方米),418平方米=41800平方分米,2×2=4(平方分米),41800÷4=10450块。
第三单元 长方体和正方体
3.2 长方体和正方体的表面积
1.复习旧知。
课题引入
6
(1)长方体有( )个面,一般都是( ),相对的面的( )相等;
(2)正方体有( )个面,它们都是( ),正方形各面的( )相等;
(3)这是一个( ),它的长( )厘米,宽( )厘米,高( )厘米,
它的棱长之和是( )厘米;
第(3)题 第(4)题
(4)这是一个( ),它的棱长是( )分米,它的棱长之和是( )分米。
长方形
面积
6
正方形
面积
长方体
8
4
60
3
正方体
5
60
今天,我们长方体和正方体特征的基础上,学习长方体和正方体的表面积。
教学新知
例1:请大家想一下,做一只这样的纸盒要用多少平方厘米的硬纸板?
说说估计的方法。
【答案】(1)20×2+10×2+8×2=76(c㎡),上下两个面的面积,前后两个面的面积,左右两个面的面积,加起来就是六个面的总面积。(2)(20+10+8)×2=76(c㎡)上面、前面和左面三个面的面积的和,再乘2。(3)20+20+10+10+8+8=76(c㎡),把六个面的面积加起来。
【结论】根据长方体有6个面,相对的面的面积相等,从而求出长方体六个面的面积的和。
教学新知
例2:什么是表面积?
将长方体和正方体展开:
【结论】长方体或正方体6个面的总面积,叫做它的表面积。
教学新知
例3:做一个微波炉的包装箱(如下图),至少要用多少平方米的
硬纸板?
上、下每个面,长 ,宽 ,面积是 ;
前、后每个面,长 ,宽 ,面积是 ;
左、右每个面,长 ,宽 ,面积是 。
0.7m
0.5m
0.35㎡
0.7m
0.4m
0.28㎡
0.5m
0.4m
0.2㎡
教学新知
【答案】(1)先用0.7×0.5求出上面的面积,再乘2,求出上下两个面的面积;用0.7×0.4求出前面的面积,再乘2,求出前后两个面的面积;用0.5×0.4求出左面的面积,再乘2,求出左右两个面的面积;再把乘得的积相加。
0.7×0.5×2+0.7×0.4×2+0.5×0.4×2
=0.7+0.56+0.4
=1.66(㎡)
(2)先求出上面、前面和左面三个面的面积的和,再乘2。
(0.7×0.5+0.7×0.4+0.5×0.4)×2
=(0.35+0.28+0.2)×2
=0.83×2
=1.66(㎡)
教学新知
【补充】大家恐怕都知道,长方体表面积是“长×宽×2+宽×高×2+长×高×2”,正方体表面积是“棱长×棱长×6”。但是在生活中可不能就这样生搬硬套,因为书上告诉你的是一般情况,生活中不是这样,有时,可能不用六个面全算。比如,让你给教室刷漆,人们常识性的只会刷上、左右、前后五个面,而你把公式套上去后,就可能连地面也给刷了,这个要注意。下面还有一个实例。
健身中心新建一个游泳池,该游泳池的长50m,宽20m,深2.5m(也就是公式中所说的高),现在让你贴上瓷砖,需要多少瓷砖?
首先,咱们得分析这道题,当然,最好的方法是联系生活实际,展开想象。既然是游泳池,肯定要求底面积,那就用长×宽求得底面积,大家可能会奇怪,为什么不铺上面呢?因为上面是水,铺上的话就不叫游泳池了。四周肯定也要铺,用宽×高×2+长×高×2就得出需要铺多少平方米的地砖了。
所以,其最终结果是1625平方米的地砖。还要注意地砖和游泳池面积的平方米是否一致,不一致还要换算单位。所以说,在解决实际问题时,正方体和长方体的表面积公式只是“半成品”,其中的很多情况是需要你仔细思考的。
资料补充:生活中的长方体和正方体
知识要点
长方体或正方体6个面的总面积,叫做它的表面积。
计算方法:
0.7×0.5 +0.7×0.5+0.5×0.4+0.5×0.4+0.7×0.4+0.7×0.4
0.7×0.5×2+0.5×0.4×2+0.7×0.4×2
(0.7×0.5 +0.5×0.4+0.7×0.4)×2
知识点1:长方体或正方体6个面的总面积,叫做它的表面积。
知识梳理
例 1:一个长方体的形状如图(单位:米):
(1)它的上下两个面的面积=( )×( )×( )。
(2)它的前后两个面的面积=( )×( )×( )。
(3)它的左右两个面的面积=( )×( )×( )。
(4)这个长方体的表面积是( )平方米。
348
15 4 2
15 6 2
4 6 2
知识梳理
小练习:
1.一个长方体的长是6分米,宽1.5分米,高3分米,它的
表面积是( )平方分米。
2.一个正方体的棱长是0.5分米,它的表面积是( )平方分米。
3.一个长4分米、宽2分米、高2分米的长方体,它占地面积最
大是多少?表面积又是多少?
63
1.5
【答案】占地面积最大是4×2=8平方分米;
表面积是(4×2+4×2+2×2)×2=40平方分米。
1.长方体或正方体( )个面的总面积,叫做它们的表面积。
2.计算正方体的表面积可以用( )的方法计算。这是因
为正方体有( )个面,每个面都是( )形,而且( )都相等。
3.一个正方体的表面积是36平方厘米,把它放在桌子上占的面积是( )平方厘米。
4.一个长方体长5厘米,宽5厘米,高4厘米,这个长方体有2个面是( )形,有( )个面的面积相等,长方体的表面积是( )。
课堂练习
6
棱长×棱长×6
6
正方
面积
6
正方
4
130平方厘米
5.做一个不带盖的长方体铁盒,长0.6米,宽0.35米,高0,4米。
至少需要多少平方米铁皮?
课堂练习
【解析】长方体的表面积是长方体6个面的总面积。题目中给出的是做一个不带盖的长方体铁盒,由此可以知道这个长方体铁盒只有5个面,没有上面。根据长方体表面积的计算方法,做这个铁盒至少需要0.6×0.35+(0.6×0.4+0.35×0.4)×2=0.97平方米铁皮。
【答案】0.6×0.35+(0.6×0.4+0.35×0.4)×2=0.97平方米
答:至少需要0.97平方米铁皮。
6.把一个正方体锯成两个长方体,它的表面积增加了6平方厘米,
那么原正方体的表面积是多少平方厘米?
课堂练习
【解析】把一个正方体锯成两个长方体,它增加的表面积也就是这个正方体一个面的面积的2倍,所以其中一个面的面积为6÷2=3平方厘米,而正方体的表面积为6个面面积的总和,也就是其中一个正方形的面积×6,即3×6=18平方厘米。
【答案】8平方厘米。
1.填空。
课后习题
(1)一个长方体正好分割成3个体积相等的正方体。已知一个正方体的
表面积是3平方厘米,原长方体的表面积是( )平方厘米。
(2)把一个长、宽、高分别是5厘米、4厘米、3厘米的长方体截成两个
小长方体,表面积最多增加( )平方厘米、
(3)把六个棱长为3厘米的正方体拼成一个长方体,表面积最多减少( )
平方厘米。
(4)一个长方体木块的表面积是60平方厘米,现在正好把它锯成两个相等
的正方体。每个正方体的表面积是( )平方厘米。
7
40
90
36
课后习题
2.判断。
(1)若一个长方体和一个正方体的所有棱长之和相等,那么他们的表面积
也一定相等。 ( )
(2)一个正方体表面积是18平方厘米,把它切成2个完全相等的长方体,表
面积比原来增加了3平方厘米。 ( )
(3)把两块棱长都是2厘米的正方体拼成一个长方体,表面积减少了8平方
厘米。 ( )
(4)一根长方体木料,横截面是24平方厘米,把它锯成3段后,表面积增加
72平方厘米。 ( )
×
√
×
×
课后习题
3.一个长4米、宽3米、高2米的长方体,它占地面积最大是多少平
方米?表面积是多少平方米?
【答案】面积:4×3=12(平方米)
表面积:(4×3+4×2+3×2)×2=52(平方米)
4.有一种无盖的玻璃鱼缸,长20厘米,宽15厘米,高10厘米,做
这样一对鱼缸需要多少平方厘米的玻璃?
【答案】(20×15+20×10+15×10)×2=1300(平方厘米)
课后习题
5.用72分米长的铁丝做一个正方体的框架,然后在外面贴上一层纸,
至少需要多少平方分米的纸?
【答案】72÷12=6分米,6×6×6=216平方分米
【解析】用72分米长的铁丝做一个正方体的框架,由于正方体有12条棱,且每条棱的长度都相等,因此可以算出这个正方体框架的棱长为72÷12=6分米。现在在这个框架外面贴一层纸,要算纸的面积也就是算这个正方体的表面积,所以一共需要6×6×6=216平方分米的纸。
课后习题
6.发散思维。
【解析】应先算出这个游泳池的表面积和一块瓷砖的面积,而游泳池没有上面,因此可算出游泳池的表面积为25×10+(25×2.4+10×2.4)×2=418(平方米),418平方米=41800平方分米,一块正方形瓷砖的面积为2×2=4(平方分米),因此至少需要这种瓷砖41800÷4=10450块。
一个游泳池,长25米,宽10米,深2.4米,在游泳池的四周和池底砌瓷砖,
如果瓷砖的边长是2分米的正方形,那么至少需要这种瓷砖多少块?
【答案】25×10+(25×2.4+10×2.4)×2=418(平方米),418平方米=41800平方分米,2×2=4(平方分米),41800÷4=10450块。
