18.1.1 平行四边形的性质解答题专题训练(含答案)
文档属性
| 名称 | 18.1.1 平行四边形的性质解答题专题训练(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 422.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-06 00:00:00 | ||
图片预览


文档简介
2025年春八下数学人教版
第十八章:18.1.1平行四边形的性质
解答题专题训练
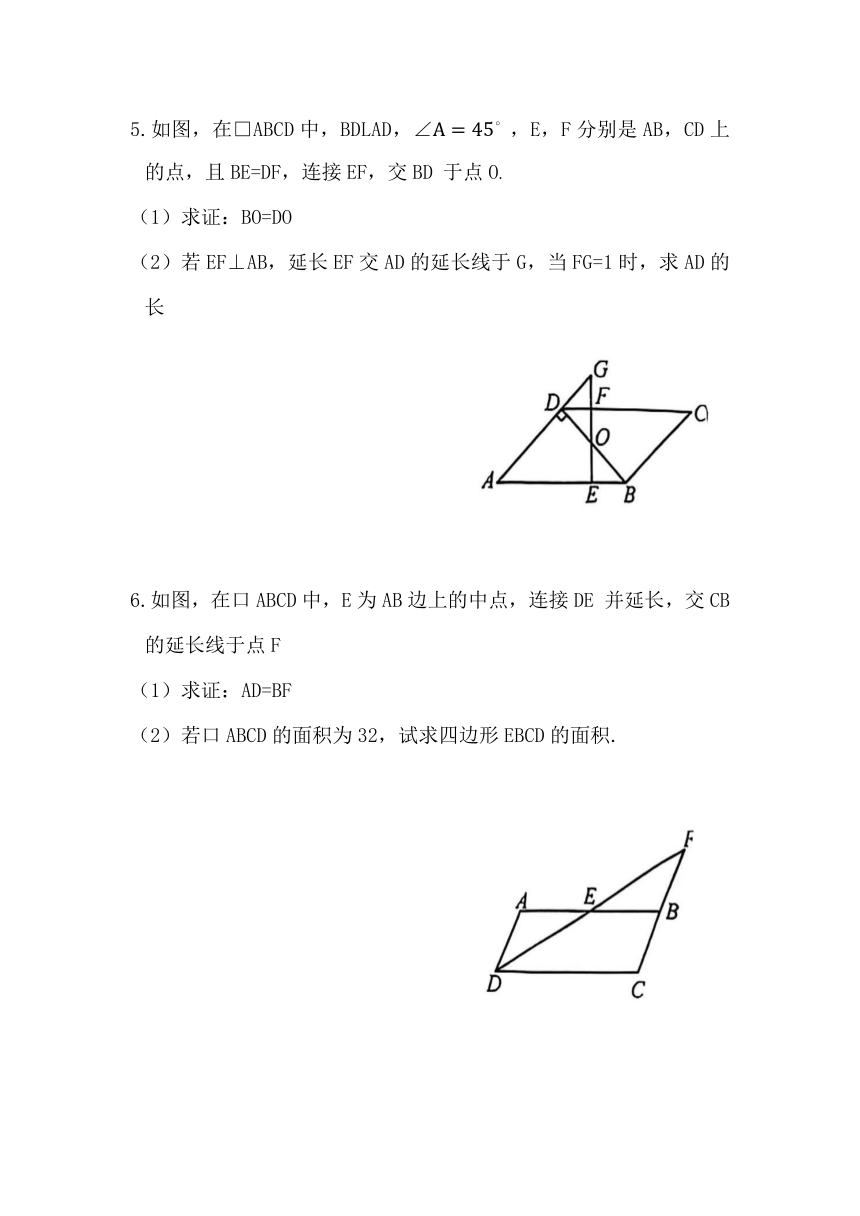
1.如图,在平行四边形ABCD中,已知对角线AC和BD相交于点O,ΔAOB的周长为15, AB=6,那么对角线AC和BD的和是多少?
2.已知:如图,四边形ABCD是平行四边形,且∠EAD=∠BAF。
(1)说明ΔCEF是等腰三角形。
(2)ΔCEF的哪两边之和等于平行四边形ABCD的周长,为什么?
3.如图,已知口ABCD的周长为60cm,对角线AC、BD相交于点O,ΔAOB的周长比ΔBOC的周长长8cm,求这个四边形各边长
4.已知,如图在ΔABC中,BD是∠ABC的平分线,DE//BC交AB 于E,EF//AC交BC于EF,则BE=F,为什么?
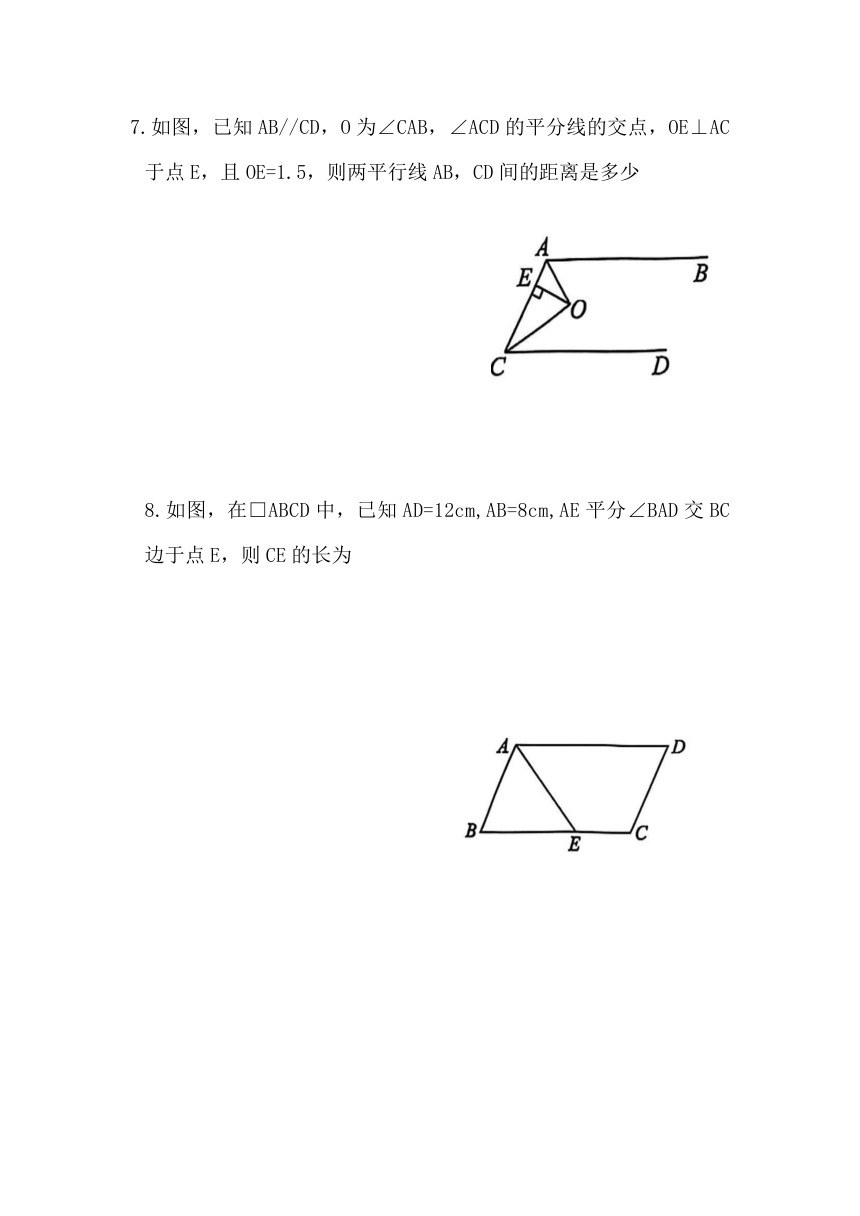
5.如图,在□ABCD中,BDLAD,,E,F分别是AB,CD上的点,且BE=DF,连接EF,交BD 于点O.
(1)求证:BO=DO
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长
6.如图,在口ABCD中,E为AB边上的中点,连接DE 并延长,交CB的延长线于点F
(1)求证:AD=BF
(2)若口ABCD的面积为32,试求四边形EBCD的面积.
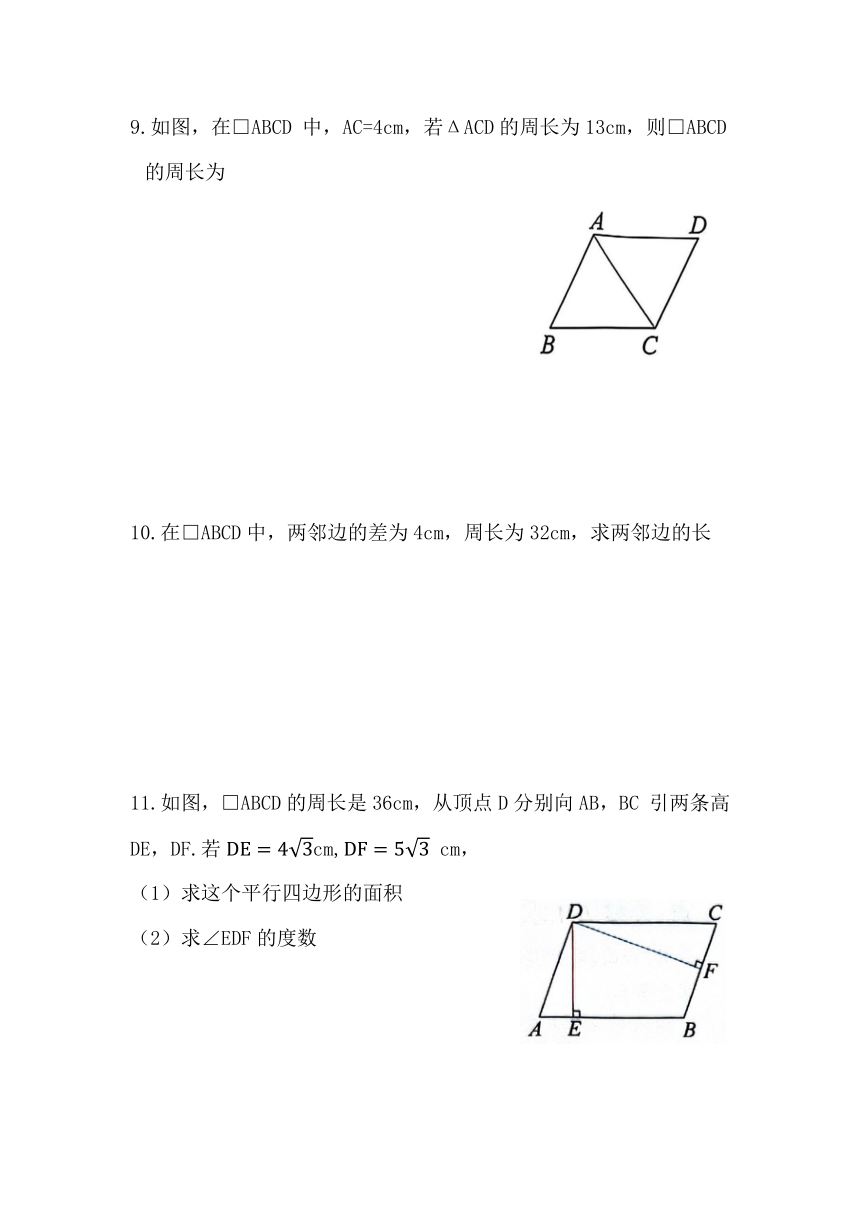
7.如图,已知AB//CD,O为∠CAB,∠ACD的平分线的交点,OE⊥AC于点E,且OE=1.5,则两平行线AB,CD间的距离是多少
8.如图,在□ABCD中,已知AD=12cm,AB=8cm,AE平分∠BAD交BC边于点E,则CE的长为
9.如图,在□ABCD 中,AC=4cm,若ΔACD的周长为13cm,则□ABCD的周长为
10.在□ABCD中,两邻边的差为4cm,周长为32cm,求两邻边的长
11.如图,□ABCD的周长是36cm,从顶点D分别向AB,BC 引两条高DE,DF.若cm, cm,
(1)求这个平行四边形的面积
(2)求∠EDF的度数
12.如图,在□ABCD中,点E,F在对角线BD上,且BE=DF
求证:∠AFE=∠CEF
13.如图,在□ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC 的延长线于点F,BGLAE,垂足为G.若,则口ABCD的面积是
14.在平行四边形ABCD中,AB=3,BC=4,∠ABC的平分线交AD于点E,∠BCD的平分线交AD于点F,则EF的长为
15.如图,在□ABCD中,,∠ABC 的平分线交AD于点E,过点D作BE的平行线交BC于点F,求∠CDF的度数
16.如图,在平行四边形ABCD中,∠ABC,∠BCD的平分线交于点E,且点E刚好落在AD上,分别延长BE,CD交于F.
(1)AB与AD之间有什么数量关系?并证明你的猜想;
(2)CE与BF之间有什么位置关系?并证明你的猜想
17.如图,在□ABCD中,DF平分∠ADC,交BC于点E,交AB的延长线于点F.
(1)求证:AD=AF
(2)若,求BF的长和ΔADF的面积.
18.如图,在□ABCD中,AD=5,BE=8,ΔDCE的面积为6,则ΔABE的面积为
19.如图,在平面直角坐标系中,A(2,0),点P为y轴上一动点,连接AP并延长至点D,使DP=AP,取y轴上一点B,以AB,AD为边作口ABCD,连接OC,则OC长度的取值范围为
20.如图,在平行四边形ABCD中,点O是对角线AC的中点,点E是BC 上一点,且AB=AE,连接EO并延长交AD于点F,过点B作AE的垂线,垂足为H,交AC于点G.
(1)求证:BE=DF.
(2)若,当CG=2时,求DF的长
答案
1.解
∵四边形ABCD是平行四边形,
∴AC=2AO, BD=2BO
∵△AOB的周长为15, AB=6
∴AB+OA+OB=15,
∴AO+OB=15-6=9,
∴AC+BD=2(AO+OB)=2×9=18.
2.解
(1)证明:∵四边形ABCD是平行四边形,
∴AB//EC,AD//FC,
所以∠BAF=∠E, ∠EAD=∠F
∴∠E=∠F
∴ΔCEF是等腰三角形
(2)∵∠EAD=∠EFC=∠FED,
∴ΔEAD是等腰三角形,
即ED=EA,
同理AB=FB,
∴ΔCEF的CE,CF两边之和等于平行四边形ABCD的周长
3.解
设AB=a, BC=b
∴a-b=8,a+b=30,
∴a=19 b=11
∴AB=DC=19cm
∴ AD=BC=11cm
4.解
∵ED//BC,EF//AC
∴ED=FC.
∵BD是∠ABC的平分线
∴∠EBD=∠FBD.
∵ED//BF
∴∠FBD=∠EDB.
∴∠EDB=∠EBD.
∴ΔEBD是等腰三角形.
∴BE=ED.
又∵ED=FC
∴BE=FC
5.解
(1)【证明】:四边形ABCD是平行四边形,
∴DC∥AB,
∴∠OBE=∠ODF
在ΔOBE和ΔODF中,
∠OBE=∠ODF
∠BOE=∠DOF
BE=DF
∴ΔOBE≌ΔODF(AAS)
∴BO=DO.
(2)【解]∵BD⊥AD
∴
∴
∴AD=DB.
∵EF⊥AB,
∴
∵EF⊥AB,DC∥AB
∴DF⊥OG,
∴
∴ΔGDF为等腰直角三角形,
∴DF=FG=1
∴
∵BD⊥AD,
∴
∴
∴
由(1)知ΔOBE≌ΔODF,
∴
∴,
∴
6.解
(1)证明:∵E为AB边上的中点,AD∥BC,
∴AE=E∠ADE=∠F.
在ΔADE与ΔBFE中,
∠ADE=∠F
∠DEA=∠FEB
AE=BE
∴ΔADE ΔBFE(AAS),
∴AD= M A
BF. (2)过点D作DM⊥AB于点M,则DM同时也是□ABCD的高.
×32=8,
∴四边形EBCD的面积=32-8=24
7.解
过点O作MN⊥AB,交AB于点M,交CD于点N,
∵AB/CD,
∴ON⊥CD,OM⊥AB,
∵AO平分∠MAC,OE⊥AC
∴OM=OE,
∵OC平分∠ACD, OE⊥AC,
∴OE=ON,
∴OM=ON,
∵OE=1.5,
∴MN=3
8.解
四边形ABCD是平行四边形,
∴AD∥B,AB=CD.
∵AD//BC
∴∠DAE=∠AEB.
∵AE平分∠BAD
∴∠DAE=∠BAE.
∴∠AEB=∠BAE
∴BE=AB=8cm.
∵AD=BC=12cm
∴CE=4cm
9.解
∵AC=4 cmΔACD的周长为13cm,
∴AD+DC=13-4=9(cm).
∴平行四边形的周长为2(AD+DC)=18cm
10.解
根据平行四边形的性质,两邻边的和为周长的一半,设两邻边分别为x,y,根据题意列出方程组,解方程组即可。
设两邻边分别为x,y,根据题意得: 解得:
11.解
(1) ∵
∴
即4AB=5BC
又∵□ABCD的周长为36
∴AB+BC=18
∴
∴
(2)在RtΔDFC中
∴
∴
∴
∴
故
12.解
证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD//CB.
∴∠ADF=∠CBE.
在ΔADF和ΔCBE中
AD=CB
∠ADF=∠CBE
DF=BE
∴ΔADF≌ΔCBE(SAS)
∴∠DFA=∠BEC.
∴∠AFE=∠CEF
13.解
解:如图,过点A作AH⊥BC于点H.
∵AE平分∠BAD,
∴∠DAE=∠BAE.
又∵四边形ABCD是平行四边形,
∴AD//BC,
∴∠BEA=∠DAE=∠BAE,
∴AB=BE=6.
∵BG⊥AE,
∴AE=2AG.
在RtΔABG中,∵AB=6 ,
∴AG=2,
∴AE=2AG=4.
∴
∴
∴
∴
14.解
∵平行四边形ABCD,
∴∠DFC=∠FCB,
又CF平分∠BCD
∴∠DCF=∠FCB,
∴∠DFC=∠DCF,
∴DF=DC,
同理可证: AE=AB,
∴2AB-BC=AE+FD-BC=EF=2
15.解
∵BE是∠ABC的平分线,
∴
在□ABCD中,
∵AD//BC,
∴
∵DF//BE,
∴
∴
16.解
(1)结论: AD=2AB.
∵BF平分∠ABC,
∴∠ABE=∠FBC,
∵四边形ABCD是平行四边形,
∴AD//BC,AB=CD,
∴∠FBC=∠AEB,
∴∠AEB=∠ABE,
AB=AE,,同理可证: CD=DE,
∴AD=AE+ED=AB+CD=2AB.
(2)结论:CE⊥BF.
理由:∵BF平分∠ABC,
∴∠ABC=2∠EBC,
CE平分∠BCD,
∴∠BCD=2∠BCE,
∵四边形ABCD是平行四边形,
∴AB//CD,
∴
∴
∴
∴
17.解
(1)证明:在□ABCD中,
∵AB//CD
∴∠CDE=∠F
∵DF 平分∠ADC
∴∠ADE=∠CDE
∴∠F=∠ADF
∴AD=AF.
解:∵AD=AF=6,AB=3
∴BF=AF-AB=3
过点D作DH⊥AF交FA的延长线于点H
∵BAD=
∴
∴
∴
∴
∴
18.解
∵四边形ABCD是平行四边形,
∴AD//BC, BC=AD=5,
∴CE=BE-BC=8-5=3,
设AD和BC的距离是h,
∴
∴h=4,
∴
19.解
∵A(2,0),
∴OA=2,
如图,过点D作x轴的平行线交y轴于点F,过点C作y轴的平行线交FD于点E,
∴∠OAP=∠FDP,
∵∠APO=∠DPF, AP=DP,
∴ΔAOP≌ΔDFP(ASA),
∴OA=DF=2,
在□ABCD中, AB=CD,
EF//OA,
∴
∵DC//AB,
∴
∠EDA+∠OAD∠CDA∠BAD=0,
∴∠EDA∠CDA=∠BAD∠OAD,
∴∠EDC=∠OAB,
CD=BA,
∴ΔECD≌ΔOBA(AAS)
∴DE=OA=2,
EF=DE+DF=4,
∵CE⊥EF,EF//y轴,.C点始终在平行于轴的直线上运动,并且这条直线与y 轴的距离为4,
则O到这条直线的距离为4,
∴OC长度的取值范围为OC≥4
20解
(1))∵AH=3 HE=1,
∴AB=AE=4,
又∵RtΔABH中,
∴
(2)如图,过A作AM⊥BC于M,,交BG于K,过G作GN⊥BC于N,则
∵
∴
∵AB=AE,
∴BE ∠BAM=∠EAM,
又∵AE⊥BG,
∴,而∠AKH=∠BKM
∴∠MAE=∠NBG,设
∠BAM=∠MAE=∠NBG=α, 则
∴AB=BG,
∴AE=BG,
在△AME和ΔBNG中
∠AME=∠BNG
∠MAE=∠NBG
AE=BG
∴ΔAME≌ΔBNG(AAS),
∴ME=NG,
在等腰RtΔCNG中,NG=NC,
∴
∴
∵O是AC的中点
∴OA=OC
∵四边形ABCD是平行四边形
∴AD//BC, AD=BC
∴∠OAF=∠OCE
∠AFO=∠CEO
∴ΔAFO≌ΔCEO(AAS)
∴AF=CE
∴AD-AF=BC-EC
即DF=BE
∴
第十八章:18.1.1平行四边形的性质
解答题专题训练
1.如图,在平行四边形ABCD中,已知对角线AC和BD相交于点O,ΔAOB的周长为15, AB=6,那么对角线AC和BD的和是多少?
2.已知:如图,四边形ABCD是平行四边形,且∠EAD=∠BAF。
(1)说明ΔCEF是等腰三角形。
(2)ΔCEF的哪两边之和等于平行四边形ABCD的周长,为什么?
3.如图,已知口ABCD的周长为60cm,对角线AC、BD相交于点O,ΔAOB的周长比ΔBOC的周长长8cm,求这个四边形各边长
4.已知,如图在ΔABC中,BD是∠ABC的平分线,DE//BC交AB 于E,EF//AC交BC于EF,则BE=F,为什么?
5.如图,在□ABCD中,BDLAD,,E,F分别是AB,CD上的点,且BE=DF,连接EF,交BD 于点O.
(1)求证:BO=DO
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长
6.如图,在口ABCD中,E为AB边上的中点,连接DE 并延长,交CB的延长线于点F
(1)求证:AD=BF
(2)若口ABCD的面积为32,试求四边形EBCD的面积.
7.如图,已知AB//CD,O为∠CAB,∠ACD的平分线的交点,OE⊥AC于点E,且OE=1.5,则两平行线AB,CD间的距离是多少
8.如图,在□ABCD中,已知AD=12cm,AB=8cm,AE平分∠BAD交BC边于点E,则CE的长为
9.如图,在□ABCD 中,AC=4cm,若ΔACD的周长为13cm,则□ABCD的周长为
10.在□ABCD中,两邻边的差为4cm,周长为32cm,求两邻边的长
11.如图,□ABCD的周长是36cm,从顶点D分别向AB,BC 引两条高DE,DF.若cm, cm,
(1)求这个平行四边形的面积
(2)求∠EDF的度数
12.如图,在□ABCD中,点E,F在对角线BD上,且BE=DF
求证:∠AFE=∠CEF
13.如图,在□ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC 的延长线于点F,BGLAE,垂足为G.若,则口ABCD的面积是
14.在平行四边形ABCD中,AB=3,BC=4,∠ABC的平分线交AD于点E,∠BCD的平分线交AD于点F,则EF的长为
15.如图,在□ABCD中,,∠ABC 的平分线交AD于点E,过点D作BE的平行线交BC于点F,求∠CDF的度数
16.如图,在平行四边形ABCD中,∠ABC,∠BCD的平分线交于点E,且点E刚好落在AD上,分别延长BE,CD交于F.
(1)AB与AD之间有什么数量关系?并证明你的猜想;
(2)CE与BF之间有什么位置关系?并证明你的猜想
17.如图,在□ABCD中,DF平分∠ADC,交BC于点E,交AB的延长线于点F.
(1)求证:AD=AF
(2)若,求BF的长和ΔADF的面积.
18.如图,在□ABCD中,AD=5,BE=8,ΔDCE的面积为6,则ΔABE的面积为
19.如图,在平面直角坐标系中,A(2,0),点P为y轴上一动点,连接AP并延长至点D,使DP=AP,取y轴上一点B,以AB,AD为边作口ABCD,连接OC,则OC长度的取值范围为
20.如图,在平行四边形ABCD中,点O是对角线AC的中点,点E是BC 上一点,且AB=AE,连接EO并延长交AD于点F,过点B作AE的垂线,垂足为H,交AC于点G.
(1)求证:BE=DF.
(2)若,当CG=2时,求DF的长
答案
1.解
∵四边形ABCD是平行四边形,
∴AC=2AO, BD=2BO
∵△AOB的周长为15, AB=6
∴AB+OA+OB=15,
∴AO+OB=15-6=9,
∴AC+BD=2(AO+OB)=2×9=18.
2.解
(1)证明:∵四边形ABCD是平行四边形,
∴AB//EC,AD//FC,
所以∠BAF=∠E, ∠EAD=∠F
∴∠E=∠F
∴ΔCEF是等腰三角形
(2)∵∠EAD=∠EFC=∠FED,
∴ΔEAD是等腰三角形,
即ED=EA,
同理AB=FB,
∴ΔCEF的CE,CF两边之和等于平行四边形ABCD的周长
3.解
设AB=a, BC=b
∴a-b=8,a+b=30,
∴a=19 b=11
∴AB=DC=19cm
∴ AD=BC=11cm
4.解
∵ED//BC,EF//AC
∴ED=FC.
∵BD是∠ABC的平分线
∴∠EBD=∠FBD.
∵ED//BF
∴∠FBD=∠EDB.
∴∠EDB=∠EBD.
∴ΔEBD是等腰三角形.
∴BE=ED.
又∵ED=FC
∴BE=FC
5.解
(1)【证明】:四边形ABCD是平行四边形,
∴DC∥AB,
∴∠OBE=∠ODF
在ΔOBE和ΔODF中,
∠OBE=∠ODF
∠BOE=∠DOF
BE=DF
∴ΔOBE≌ΔODF(AAS)
∴BO=DO.
(2)【解]∵BD⊥AD
∴
∴
∴AD=DB.
∵EF⊥AB,
∴
∵EF⊥AB,DC∥AB
∴DF⊥OG,
∴
∴ΔGDF为等腰直角三角形,
∴DF=FG=1
∴
∵BD⊥AD,
∴
∴
∴
由(1)知ΔOBE≌ΔODF,
∴
∴,
∴
6.解
(1)证明:∵E为AB边上的中点,AD∥BC,
∴AE=E∠ADE=∠F.
在ΔADE与ΔBFE中,
∠ADE=∠F
∠DEA=∠FEB
AE=BE
∴ΔADE ΔBFE(AAS),
∴AD= M A
BF. (2)过点D作DM⊥AB于点M,则DM同时也是□ABCD的高.
×32=8,
∴四边形EBCD的面积=32-8=24
7.解
过点O作MN⊥AB,交AB于点M,交CD于点N,
∵AB/CD,
∴ON⊥CD,OM⊥AB,
∵AO平分∠MAC,OE⊥AC
∴OM=OE,
∵OC平分∠ACD, OE⊥AC,
∴OE=ON,
∴OM=ON,
∵OE=1.5,
∴MN=3
8.解
四边形ABCD是平行四边形,
∴AD∥B,AB=CD.
∵AD//BC
∴∠DAE=∠AEB.
∵AE平分∠BAD
∴∠DAE=∠BAE.
∴∠AEB=∠BAE
∴BE=AB=8cm.
∵AD=BC=12cm
∴CE=4cm
9.解
∵AC=4 cmΔACD的周长为13cm,
∴AD+DC=13-4=9(cm).
∴平行四边形的周长为2(AD+DC)=18cm
10.解
根据平行四边形的性质,两邻边的和为周长的一半,设两邻边分别为x,y,根据题意列出方程组,解方程组即可。
设两邻边分别为x,y,根据题意得: 解得:
11.解
(1) ∵
∴
即4AB=5BC
又∵□ABCD的周长为36
∴AB+BC=18
∴
∴
(2)在RtΔDFC中
∴
∴
∴
∴
故
12.解
证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD//CB.
∴∠ADF=∠CBE.
在ΔADF和ΔCBE中
AD=CB
∠ADF=∠CBE
DF=BE
∴ΔADF≌ΔCBE(SAS)
∴∠DFA=∠BEC.
∴∠AFE=∠CEF
13.解
解:如图,过点A作AH⊥BC于点H.
∵AE平分∠BAD,
∴∠DAE=∠BAE.
又∵四边形ABCD是平行四边形,
∴AD//BC,
∴∠BEA=∠DAE=∠BAE,
∴AB=BE=6.
∵BG⊥AE,
∴AE=2AG.
在RtΔABG中,∵AB=6 ,
∴AG=2,
∴AE=2AG=4.
∴
∴
∴
∴
14.解
∵平行四边形ABCD,
∴∠DFC=∠FCB,
又CF平分∠BCD
∴∠DCF=∠FCB,
∴∠DFC=∠DCF,
∴DF=DC,
同理可证: AE=AB,
∴2AB-BC=AE+FD-BC=EF=2
15.解
∵BE是∠ABC的平分线,
∴
在□ABCD中,
∵AD//BC,
∴
∵DF//BE,
∴
∴
16.解
(1)结论: AD=2AB.
∵BF平分∠ABC,
∴∠ABE=∠FBC,
∵四边形ABCD是平行四边形,
∴AD//BC,AB=CD,
∴∠FBC=∠AEB,
∴∠AEB=∠ABE,
AB=AE,,同理可证: CD=DE,
∴AD=AE+ED=AB+CD=2AB.
(2)结论:CE⊥BF.
理由:∵BF平分∠ABC,
∴∠ABC=2∠EBC,
CE平分∠BCD,
∴∠BCD=2∠BCE,
∵四边形ABCD是平行四边形,
∴AB//CD,
∴
∴
∴
∴
17.解
(1)证明:在□ABCD中,
∵AB//CD
∴∠CDE=∠F
∵DF 平分∠ADC
∴∠ADE=∠CDE
∴∠F=∠ADF
∴AD=AF.
解:∵AD=AF=6,AB=3
∴BF=AF-AB=3
过点D作DH⊥AF交FA的延长线于点H
∵BAD=
∴
∴
∴
∴
∴
18.解
∵四边形ABCD是平行四边形,
∴AD//BC, BC=AD=5,
∴CE=BE-BC=8-5=3,
设AD和BC的距离是h,
∴
∴h=4,
∴
19.解
∵A(2,0),
∴OA=2,
如图,过点D作x轴的平行线交y轴于点F,过点C作y轴的平行线交FD于点E,
∴∠OAP=∠FDP,
∵∠APO=∠DPF, AP=DP,
∴ΔAOP≌ΔDFP(ASA),
∴OA=DF=2,
在□ABCD中, AB=CD,
EF//OA,
∴
∵DC//AB,
∴
∠EDA+∠OAD∠CDA∠BAD=0,
∴∠EDA∠CDA=∠BAD∠OAD,
∴∠EDC=∠OAB,
CD=BA,
∴ΔECD≌ΔOBA(AAS)
∴DE=OA=2,
EF=DE+DF=4,
∵CE⊥EF,EF//y轴,.C点始终在平行于轴的直线上运动,并且这条直线与y 轴的距离为4,
则O到这条直线的距离为4,
∴OC长度的取值范围为OC≥4
20解
(1))∵AH=3 HE=1,
∴AB=AE=4,
又∵RtΔABH中,
∴
(2)如图,过A作AM⊥BC于M,,交BG于K,过G作GN⊥BC于N,则
∵
∴
∵AB=AE,
∴BE ∠BAM=∠EAM,
又∵AE⊥BG,
∴,而∠AKH=∠BKM
∴∠MAE=∠NBG,设
∠BAM=∠MAE=∠NBG=α, 则
∴AB=BG,
∴AE=BG,
在△AME和ΔBNG中
∠AME=∠BNG
∠MAE=∠NBG
AE=BG
∴ΔAME≌ΔBNG(AAS),
∴ME=NG,
在等腰RtΔCNG中,NG=NC,
∴
∴
∵O是AC的中点
∴OA=OC
∵四边形ABCD是平行四边形
∴AD//BC, AD=BC
∴∠OAF=∠OCE
∠AFO=∠CEO
∴ΔAFO≌ΔCEO(AAS)
∴AF=CE
∴AD-AF=BC-EC
即DF=BE
∴
