求线段最值典型考点 专项练 2025年中考数学一轮复习备考
文档属性
| 名称 | 求线段最值典型考点 专项练 2025年中考数学一轮复习备考 |  | |
| 格式 | docx | ||
| 文件大小 | 986.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-05 17:20:48 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
求线段最值典型考点 专项练
2025年中考数学一轮复习备考
一、填空题
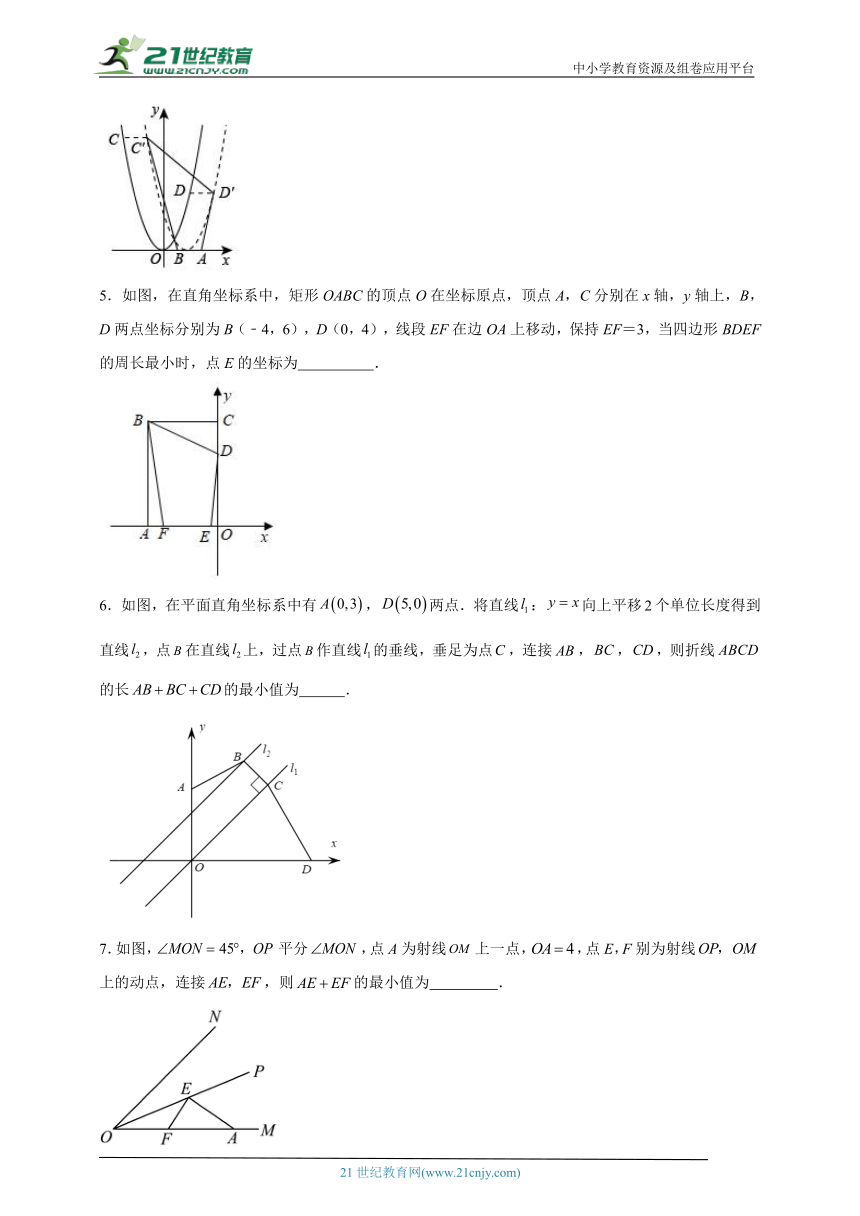
1.如图,在矩形中,,点E在直线上,从点A出发向右运动,速度为每秒,点F在直线上,从点B出发向右运动,速度为每秒2cm,相交于点G,则的最小值为 cm.
2.探究式子的最小值.小胖同学运用“数形结合”的思想:如图,取,作于.于,且,,点在上,设,则,于是,,,因此,可求得的最小值为 ,已知,则的最大值是 .
3.如图,在平面直角坐标系中,已知,在x轴上取两点C,D(点C在点D左侧),且始终保持,线段在x轴上平移,当的值最小时,点C的坐标为 .
4.如图,已知点,,两点,在抛物线上,向左或向右平移抛物线后,,的对应点分别为,,当四边形的周长最小时,抛物线的解析式为 .
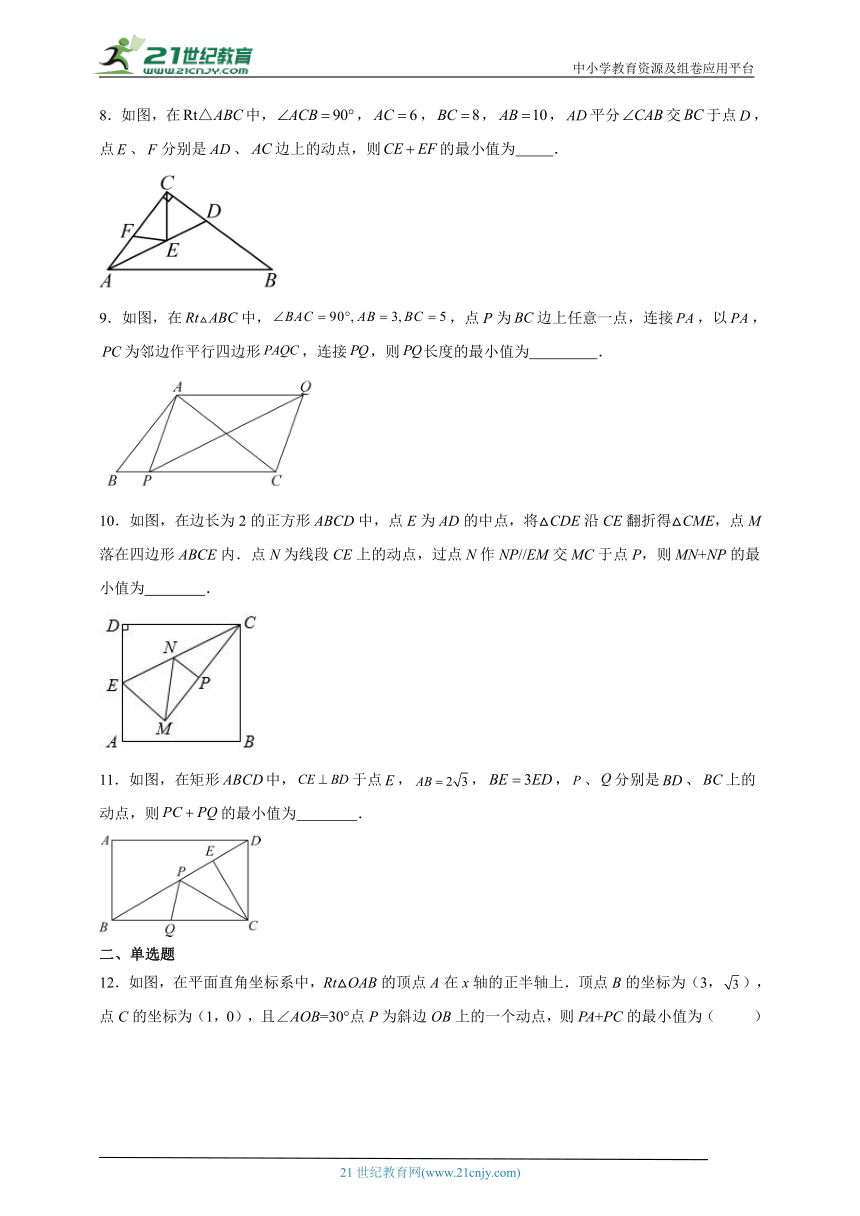
5.如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,顶点A,C分别在x轴,y轴上,B,D两点坐标分别为B(﹣4,6),D(0,4),线段EF在边OA上移动,保持EF=3,当四边形BDEF的周长最小时,点E的坐标为 .
6.如图,在平面直角坐标系中有,两点.将直线:向上平移个单位长度得到直线,点在直线上,过点作直线的垂线,垂足为点,连接,,,则折线的长的最小值为 .
7.如图,平分,点A为射线上一点,,点E,F别为射线上的动点,连接,则的最小值为 .
8.如图,在中,,,,,平分交于点,点、分别是、边上的动点,则的最小值为 .
9.如图,在中,,点P为边上任意一点,连接,以,为邻边作平行四边形,连接,则长度的最小值为 .
10.如图,在边长为2的正方形ABCD中,点E为AD的中点,将△CDE沿CE翻折得△CME,点M落在四边形ABCE内.点N为线段CE上的动点,过点N作NP//EM交MC于点P,则MN+NP的最小值为 .
11.如图,在矩形中,于点,,,、分别是、上的动点,则的最小值为 .
二、单选题
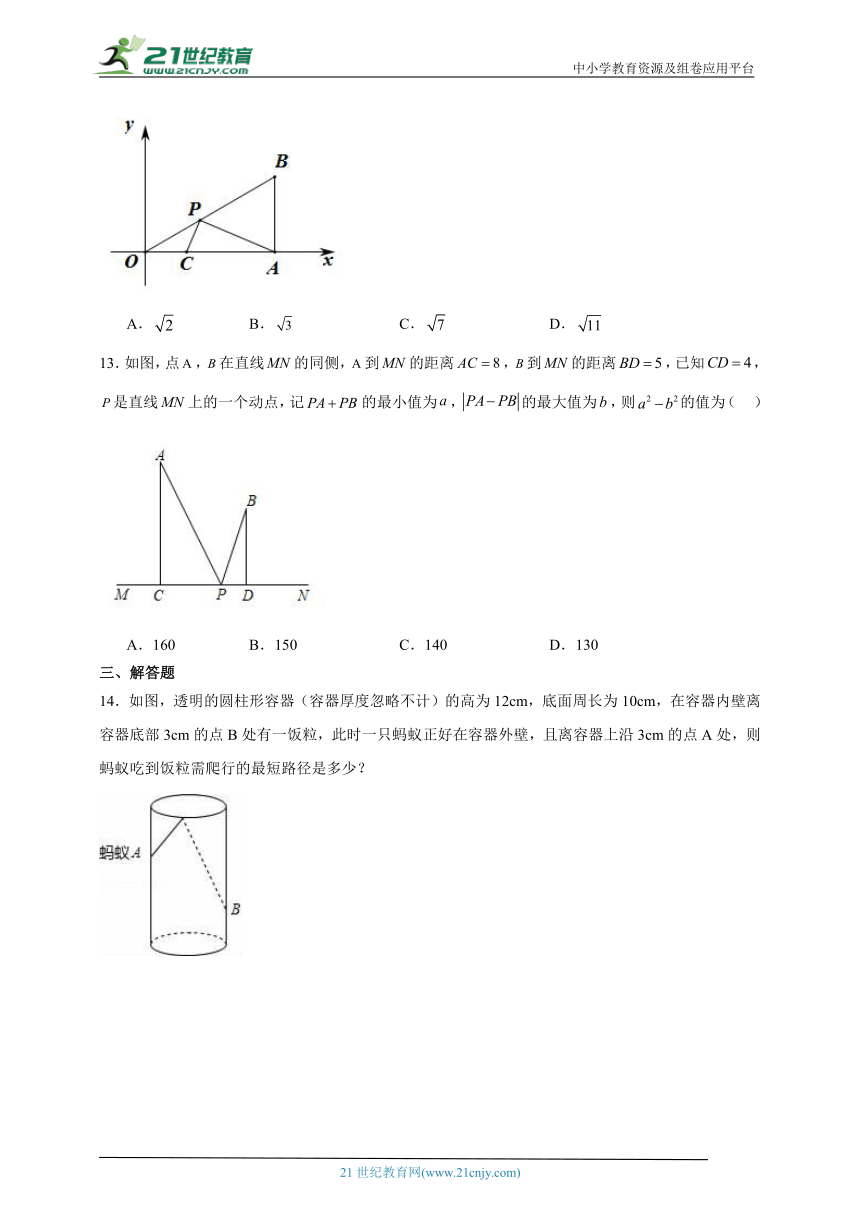
12.如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上.顶点B的坐标为(3,),点C的坐标为(1,0),且∠AOB=30°点P为斜边OB上的一个动点,则PA+PC的最小值为( )
A. B. C. D.
13.如图,点,在直线的同侧,到的距离,到的距离,已知,是直线上的一个动点,记的最小值为,的最大值为,则的值为( )
A.160 B.150 C.140 D.130
三、解答题
14.如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是多少?
参考答案
1.10
解:∵点E在直线上,从点A出发向右运动,速度为每秒,点F在直线上,从点B出发向右运动,速度为每秒,
∴,
∵四边形是矩形,
∴,
∴点G到的距离与点G到的距离之比为,
∵,
∴点G到的距离为,
过点G作直线平行,分别交于点M,N,
即点G的运动路线为直线,
作点B关于的对称点,连接,,
则,,
∴,
∴的最小值为的长;
在中,
∵,
∴,
∴的最小值为,
故答案为:10.
2.
解:如图,作关于的对称点,连接交于,连接,
,
则,,
此时的值最小为:,
,,
,
,
四边形是平行四边形,
,
四边形是矩形,
,,
,
如图,,
,
则,
,
的最大值为的长度,
过点作交于,
则四边形为矩形,
,
,
,
的最大值为,
故答案为: ,.
3.(-1,0)
解:如图,作点B关于x轴的对称点B′,将B′向右平移1个单位得到B″,连接AB″,与x轴交于点D,过点B′作AB″的平行线,与x轴交于点C,
可知四边形B′B″DC为平行四边形,
则B′C=B″D,
由对称性质可得:BC=B′C,
∴AD+BC=AD+B′C=AD+B″D=AB″,
则此时AB″最小,即AD+BC最小,
∵A(3,6),B(-2,2),
∴B′(-2,-2),
∴B″(-1,-2),
设直线AB″的表达式为:y=kx+b,
则,解得:,
∴直线AB″的表达式为:y=2x,
令y=0,解得:x=0,即点D坐标为(0,0),
∴点C坐标为(-1,0),
故答案为:(-1,0).
4..
解:∵,,,,
∴,,
由平移的性质可知:,
∴四边形的周长为;
要使其周长最小,则应使的值最小;
设抛物线平移了a个单位,当a>0时,抛物线向右平移,当a<0时,抛物线向左平移;
∴,,
将向左平移2个单位得到,则由平移的性质可知:,
将关于x轴的对称点记为点E,则,由轴对称性质可知,,
∴,
当B、E、三点共线时,的值最小,
设直线的解析式为:,
∴,
当时,
∴
∴,
将E点坐标代入解析式可得:,
解得:,
此时,
此时四边形的周长为;
当时,,,,,
此时四边形的周长为:
;
∵,
∴当时,其周长最小,
所以抛物线向右平移了个单位,
所以其解析式为:;
故答案为:.
5.
解:如图所示,∵D(0,4),
∴D点关于x轴的对称点坐标为H(0,-4),
∴ED=EH,
将点H向左平移3个单位,得到点G(-3,-4),
∴EF=HG,EF∥HG,
∴四边形EFGH是平行四边形,
∴EH=FG,
∴FG =ED,
∵B(-4,6),
∴BD=,
又∵EF=3,
∴四边形BDEF的周长=BD+DE+EF+BF=+FG+3+BF,
要使四边形BDEF的周长最小,则应使FG+BF的值最小,
而当F、G、B三点共线时FG+BF的值最小,
设直线BG的解析式为:
∵B(-4,6),G(-3,-4),
∴,
∴,
∴,
当y=0时,,
∴,
∴
故答案为:.
【点睛】
6.
解:如图,将点沿轴向下平移个单位得到,以为斜边,作等腰直角三角形,则点,连接,
是等腰直角三角形,
,,
将直线:向上平移个单位长度得到直线,
,,
,,
,
,,
,
四边形是平行四边形,
,
,
当点,点,点三点共线时,有最小值为的长,即有最小值,
点,点,
,
折线的长的最小值为,
故答案为:.
7.
解:如图,在上截取,连接,过点A作于点H.
,,
,
,
.
,,
.
故答案为:.
8.
解:在上取一点,使得,连接,
∵平分,
∴,
∵是公共边,
∴,
∴,
∴,
当点,,在同一条直线上且时,有最小值,即最小,其值为,
∵,
∴,
∴最小值为.
故答案为:.
9./2.4
解:∵,
∴,
∵四边形APCQ是平行四边形,
∴PO=QO,CO=AO,
∵PQ最短也就是PO最短,
∴过O作BC的垂线,
∵,
∴,
∴,
∴,
∴,
∴则PQ的最小值为,
故答案为:.
10.
解:作点P关于CE的对称点P′,
由折叠的性质知CE是∠DCM的平分线,
∴点P′在CD上,
过点M作MF⊥CD于F,交CE于点G,
∵MN+NP=MN+NP′≤MF,
∴MN+NP的最小值为MF的长,
连接DG,DM,
由折叠的性质知CE为线段 DM的垂直平分线,
∵AD=CD=2,DE=1,
∴CE==,
∵CE×DO=CD×DE,
∴DO=,
∴EO=,
∵MF⊥CD,∠EDC=90°,
∴DE∥MF,
∴∠EDO=∠GMO,
∵CE为线段DM的垂直平分线,
∴DO=OM,∠DOE=∠MOG=90°,
∴△DOE≌△MOG,
∴DE=GM,
∴四边形DEMG为平行四边形,
∵∠MOG=90°,
∴四边形DEMG为菱形,
∴EG=2OE=,GM= DE=1,
∴CG=,
∵DE∥MF,即DE∥GF,
∴△CFG∽△CDE,
∴,即,
∴FG=,
∴MF=1+=,
∴MN+NP的最小值为.
故答案为:.
11.
解:∵在矩形中,,,,
∴,,,
∵,,,
∴,
∴,
∴,
∴,
解得:或(负值不符合题意,舍去),
∴,
∴,
如图,延长至点,使,过点作于点,交于点,连接,
∵,
∴点和点关于对称,
∴,,
∴,
∴,当点,,共线时,的最小值为,
∵,,
∴,
∴,
在中,,
∴,
故答案为:.
12.C
解:如图,过点C作C关于OB的对称点C′,连接AC′与OB相交,
则AC′与OB的交点即所求的点P,PA+PC的最小值=AC′,
过点C′作C′D⊥OA于D,
∵点C的坐标为(1,0),且∠AOB=30°,
∴∠OCC′=90°-30°=60°,
OC=1,CC′=2×1×=1,
∴CD=,C′D=,
∵顶点B的坐标为(3,),点C的坐标为(1,0),∠OAB=90°,
∴AC=3-1=2,
∴AD=2+=,
在Rt△AC′D中,由勾股定理得,
AC′===.
13.A
解:如图所示,作点A关于直线MN的对称点,连接交直线MN于点P,则点P即为所求点,过点作直线,
∵,,,
∴,,,
在中,根据勾股定理得,
∴,
即PA+PB的最小值是;
如图所示,延长AB交MN于点,
∵,,
∴当点P运动到点时,最大,
过点B作,则,
∴,
在中,根据勾股定理得,
,
∴,
即,
∴,
14.13 cm
如图:
∵高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,
此时蚂蚁正好在容器外壁,离容器上沿3cm与饭粒相对的点A处,
∴A′D=5cm,BD=12﹣3+AE=12cm,
∴将容器侧面展开,作A关于EF的对称点A′,
连接A′B,则A′B即为最短距离,
A′B==13(cm),
即蚂蚁吃到饭粒需爬行的最短路径是13cm.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
求线段最值典型考点 专项练
2025年中考数学一轮复习备考
一、填空题
1.如图,在矩形中,,点E在直线上,从点A出发向右运动,速度为每秒,点F在直线上,从点B出发向右运动,速度为每秒2cm,相交于点G,则的最小值为 cm.
2.探究式子的最小值.小胖同学运用“数形结合”的思想:如图,取,作于.于,且,,点在上,设,则,于是,,,因此,可求得的最小值为 ,已知,则的最大值是 .
3.如图,在平面直角坐标系中,已知,在x轴上取两点C,D(点C在点D左侧),且始终保持,线段在x轴上平移,当的值最小时,点C的坐标为 .
4.如图,已知点,,两点,在抛物线上,向左或向右平移抛物线后,,的对应点分别为,,当四边形的周长最小时,抛物线的解析式为 .
5.如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,顶点A,C分别在x轴,y轴上,B,D两点坐标分别为B(﹣4,6),D(0,4),线段EF在边OA上移动,保持EF=3,当四边形BDEF的周长最小时,点E的坐标为 .
6.如图,在平面直角坐标系中有,两点.将直线:向上平移个单位长度得到直线,点在直线上,过点作直线的垂线,垂足为点,连接,,,则折线的长的最小值为 .
7.如图,平分,点A为射线上一点,,点E,F别为射线上的动点,连接,则的最小值为 .
8.如图,在中,,,,,平分交于点,点、分别是、边上的动点,则的最小值为 .
9.如图,在中,,点P为边上任意一点,连接,以,为邻边作平行四边形,连接,则长度的最小值为 .
10.如图,在边长为2的正方形ABCD中,点E为AD的中点,将△CDE沿CE翻折得△CME,点M落在四边形ABCE内.点N为线段CE上的动点,过点N作NP//EM交MC于点P,则MN+NP的最小值为 .
11.如图,在矩形中,于点,,,、分别是、上的动点,则的最小值为 .
二、单选题
12.如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上.顶点B的坐标为(3,),点C的坐标为(1,0),且∠AOB=30°点P为斜边OB上的一个动点,则PA+PC的最小值为( )
A. B. C. D.
13.如图,点,在直线的同侧,到的距离,到的距离,已知,是直线上的一个动点,记的最小值为,的最大值为,则的值为( )
A.160 B.150 C.140 D.130
三、解答题
14.如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是多少?
参考答案
1.10
解:∵点E在直线上,从点A出发向右运动,速度为每秒,点F在直线上,从点B出发向右运动,速度为每秒,
∴,
∵四边形是矩形,
∴,
∴点G到的距离与点G到的距离之比为,
∵,
∴点G到的距离为,
过点G作直线平行,分别交于点M,N,
即点G的运动路线为直线,
作点B关于的对称点,连接,,
则,,
∴,
∴的最小值为的长;
在中,
∵,
∴,
∴的最小值为,
故答案为:10.
2.
解:如图,作关于的对称点,连接交于,连接,
,
则,,
此时的值最小为:,
,,
,
,
四边形是平行四边形,
,
四边形是矩形,
,,
,
如图,,
,
则,
,
的最大值为的长度,
过点作交于,
则四边形为矩形,
,
,
,
的最大值为,
故答案为: ,.
3.(-1,0)
解:如图,作点B关于x轴的对称点B′,将B′向右平移1个单位得到B″,连接AB″,与x轴交于点D,过点B′作AB″的平行线,与x轴交于点C,
可知四边形B′B″DC为平行四边形,
则B′C=B″D,
由对称性质可得:BC=B′C,
∴AD+BC=AD+B′C=AD+B″D=AB″,
则此时AB″最小,即AD+BC最小,
∵A(3,6),B(-2,2),
∴B′(-2,-2),
∴B″(-1,-2),
设直线AB″的表达式为:y=kx+b,
则,解得:,
∴直线AB″的表达式为:y=2x,
令y=0,解得:x=0,即点D坐标为(0,0),
∴点C坐标为(-1,0),
故答案为:(-1,0).
4..
解:∵,,,,
∴,,
由平移的性质可知:,
∴四边形的周长为;
要使其周长最小,则应使的值最小;
设抛物线平移了a个单位,当a>0时,抛物线向右平移,当a<0时,抛物线向左平移;
∴,,
将向左平移2个单位得到,则由平移的性质可知:,
将关于x轴的对称点记为点E,则,由轴对称性质可知,,
∴,
当B、E、三点共线时,的值最小,
设直线的解析式为:,
∴,
当时,
∴
∴,
将E点坐标代入解析式可得:,
解得:,
此时,
此时四边形的周长为;
当时,,,,,
此时四边形的周长为:
;
∵,
∴当时,其周长最小,
所以抛物线向右平移了个单位,
所以其解析式为:;
故答案为:.
5.
解:如图所示,∵D(0,4),
∴D点关于x轴的对称点坐标为H(0,-4),
∴ED=EH,
将点H向左平移3个单位,得到点G(-3,-4),
∴EF=HG,EF∥HG,
∴四边形EFGH是平行四边形,
∴EH=FG,
∴FG =ED,
∵B(-4,6),
∴BD=,
又∵EF=3,
∴四边形BDEF的周长=BD+DE+EF+BF=+FG+3+BF,
要使四边形BDEF的周长最小,则应使FG+BF的值最小,
而当F、G、B三点共线时FG+BF的值最小,
设直线BG的解析式为:
∵B(-4,6),G(-3,-4),
∴,
∴,
∴,
当y=0时,,
∴,
∴
故答案为:.
【点睛】
6.
解:如图,将点沿轴向下平移个单位得到,以为斜边,作等腰直角三角形,则点,连接,
是等腰直角三角形,
,,
将直线:向上平移个单位长度得到直线,
,,
,,
,
,,
,
四边形是平行四边形,
,
,
当点,点,点三点共线时,有最小值为的长,即有最小值,
点,点,
,
折线的长的最小值为,
故答案为:.
7.
解:如图,在上截取,连接,过点A作于点H.
,,
,
,
.
,,
.
故答案为:.
8.
解:在上取一点,使得,连接,
∵平分,
∴,
∵是公共边,
∴,
∴,
∴,
当点,,在同一条直线上且时,有最小值,即最小,其值为,
∵,
∴,
∴最小值为.
故答案为:.
9./2.4
解:∵,
∴,
∵四边形APCQ是平行四边形,
∴PO=QO,CO=AO,
∵PQ最短也就是PO最短,
∴过O作BC的垂线,
∵,
∴,
∴,
∴,
∴,
∴则PQ的最小值为,
故答案为:.
10.
解:作点P关于CE的对称点P′,
由折叠的性质知CE是∠DCM的平分线,
∴点P′在CD上,
过点M作MF⊥CD于F,交CE于点G,
∵MN+NP=MN+NP′≤MF,
∴MN+NP的最小值为MF的长,
连接DG,DM,
由折叠的性质知CE为线段 DM的垂直平分线,
∵AD=CD=2,DE=1,
∴CE==,
∵CE×DO=CD×DE,
∴DO=,
∴EO=,
∵MF⊥CD,∠EDC=90°,
∴DE∥MF,
∴∠EDO=∠GMO,
∵CE为线段DM的垂直平分线,
∴DO=OM,∠DOE=∠MOG=90°,
∴△DOE≌△MOG,
∴DE=GM,
∴四边形DEMG为平行四边形,
∵∠MOG=90°,
∴四边形DEMG为菱形,
∴EG=2OE=,GM= DE=1,
∴CG=,
∵DE∥MF,即DE∥GF,
∴△CFG∽△CDE,
∴,即,
∴FG=,
∴MF=1+=,
∴MN+NP的最小值为.
故答案为:.
11.
解:∵在矩形中,,,,
∴,,,
∵,,,
∴,
∴,
∴,
∴,
解得:或(负值不符合题意,舍去),
∴,
∴,
如图,延长至点,使,过点作于点,交于点,连接,
∵,
∴点和点关于对称,
∴,,
∴,
∴,当点,,共线时,的最小值为,
∵,,
∴,
∴,
在中,,
∴,
故答案为:.
12.C
解:如图,过点C作C关于OB的对称点C′,连接AC′与OB相交,
则AC′与OB的交点即所求的点P,PA+PC的最小值=AC′,
过点C′作C′D⊥OA于D,
∵点C的坐标为(1,0),且∠AOB=30°,
∴∠OCC′=90°-30°=60°,
OC=1,CC′=2×1×=1,
∴CD=,C′D=,
∵顶点B的坐标为(3,),点C的坐标为(1,0),∠OAB=90°,
∴AC=3-1=2,
∴AD=2+=,
在Rt△AC′D中,由勾股定理得,
AC′===.
13.A
解:如图所示,作点A关于直线MN的对称点,连接交直线MN于点P,则点P即为所求点,过点作直线,
∵,,,
∴,,,
在中,根据勾股定理得,
∴,
即PA+PB的最小值是;
如图所示,延长AB交MN于点,
∵,,
∴当点P运动到点时,最大,
过点B作,则,
∴,
在中,根据勾股定理得,
,
∴,
即,
∴,
14.13 cm
如图:
∵高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,
此时蚂蚁正好在容器外壁,离容器上沿3cm与饭粒相对的点A处,
∴A′D=5cm,BD=12﹣3+AE=12cm,
∴将容器侧面展开,作A关于EF的对称点A′,
连接A′B,则A′B即为最短距离,
A′B==13(cm),
即蚂蚁吃到饭粒需爬行的最短路径是13cm.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
